黏弹性基体中变截面挠曲电Timoshenko纳米梁振动特性研究
吴 栋, 张大鹏, 雷勇军
(国防科技大学 空天科学学院,长沙 410073)
压电俘能器[1]能收集环境中因振动产生的机械能并将其转化为供纳米元器件使用的电能,在为纳米元器件供电方面具有极大的应用潜力。在实际的工程应用中,开展压电俘能器的振动特性研究有助于更好地发挥其工作性能。
分子动力学模拟和试验的结果均表明,压电纳米元器件的力学性能在纳米尺度下具有明显的尺度效应[2-3],经典连续介质力学因忽略了材料的尺度效应而难以准确表达压电纳米元件的力学特性[4]。非局部理论[5]的提出弥补了连续介质力学在尺度效应方面的不足,在描述纳米材料的力学行为方面得到广泛应用。刘灿昌等[6]基于线弹性非局部理论,建立轴向非线性伸长的两端固支纳米梁的动力学模型,研究非局部纳米梁的主谐波共振响应。张大鹏等[7]基于非局部黏弹性理论,建立了Euler-Bernoulli梁的振动控制方程,利用传递函数法得到了振动控制方程的解。Lei等[8-9]考虑非局部效应分别研究了外加黏弹性阻尼下Timoshenko纳米梁和Euler-Bernoulli纳米梁的动力学特性。由于结构形式对纳米梁的力学性能有较大的影响,为满足不同的应用需求,需探索不同结构形式纳米梁的振动特性。张大鹏等[10]考虑磁场的影响,基于非局部理论建立黏弹性基体上变截面纳米梁的振动控制方程,并通过联合传递函数法和摄动法求解振动控制方程。Roostai等[11]基于具有表面效应的非局部弹性理论,研究了非局部参数、表面能和轴向力对变截面纳米梁自由横向振动固有频率的影响。Rajasekaran等[12]考虑非局部效应和截面非均匀性,采用轴向功能梯度材料对梁进行建模,研究了结构的静力变形、稳定性和自由振动响应。Robinson等[13]基于具有轴向功能梯度的非局部Timoshenko梁模型,研究了非局部参数、截面非均匀性和边界条件对结构屈曲载荷的影响。有学者指出[14-16],为了更准确地预测压电纳米元件的力学性能,有必要将非局部理论与应变梯度理论相结合。Khaniki等[17]采用精确的非局部应变梯度理论,研究了变截面小尺度Euler-Bernoulli梁的屈曲行为。张英蓉等[18]基于非局部应变梯度理论,考虑纳米梁的高阶剪切变形建立其振动控制方程,并给出振动控制方程的纳维级数解。挠曲电效应考虑非均匀应变场与电场之间的耦合关系,认为非均匀应变介质材料的电极化强度受电场、应变和应变梯度的影响。但目前综合考虑非局部效应、截面非均匀性和挠曲电效应的研究还相对较少。
本文基于非局部Timoshenko梁模型,研究变截面挠曲电纳米梁在黏弹性基体中的振动特性,基于摄动理论给出典型边界条件下结构自由振动控制方程传递函数的求解方法,并通过算例对非局部参数、截面非均匀性、挠曲电系数和基体黏弹性对结构振动特性的影响规律进行分析,为压电纳米元器件的设计、分析和应用提供了理论依据。
1 振动控制方程与边界条件
黏弹性基体中变截面Timoshenko纳米梁的力学模型如图1所示。以变截面挠曲电Timoshenko纳米梁左右端面的中点连线为x轴,左端面的对称轴分别为y轴和z轴建立坐标系o-xyz,其中z轴沿着变截面挠曲电纳米梁的横向振动方向。变截面挠曲电纳米梁的长度和宽度分别为L和b,高度沿着x轴线性递减,x=0和x=L处高度分别为h1和h2,有
hx=εx+h1,x∈[0,L]
(1)
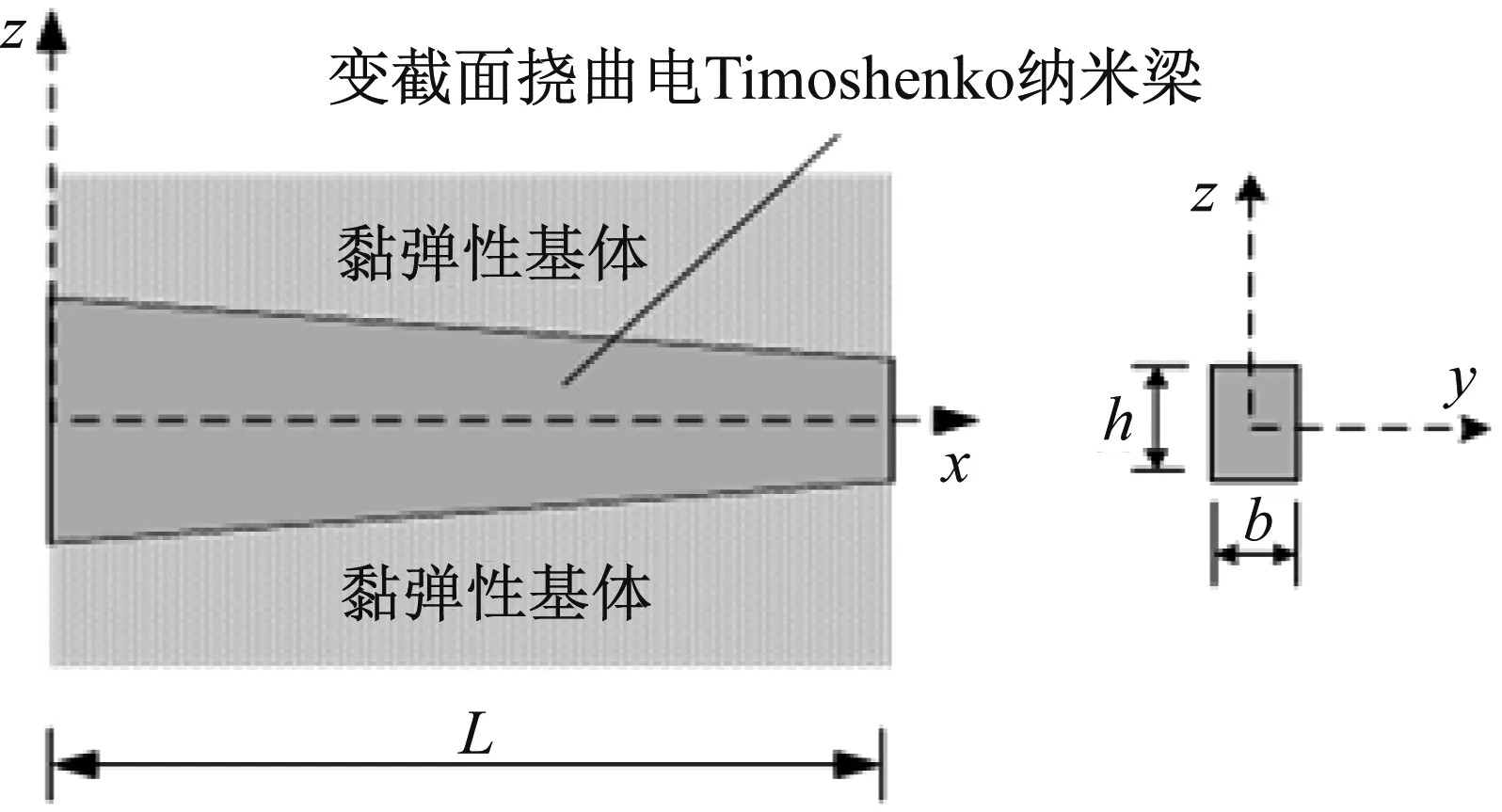
图1 黏弹性基体中变截面Timoshenko纳米梁力学模型
式中,ε=(h2-h1)/L,下标“x”表示坐标x处的物理量。黏弹性基体采用visco-Pasternak黏弹性模型模拟,该模型在经典Pasternak弹性模型的基础上考虑了黏性阻尼的影响。
变截面挠曲电纳米梁的横截面积和横截面惯性矩可分别表示为
(2)
1.1 振动控制方程
基于Yue等[19]对微尺度下等截面挠曲电Timoshenko梁的研究,并进一步考虑黏弹性基体和截面非均匀性的影响,即可得到黏弹性基体中变截面挠曲电纳米Timoshenko梁的自由振动控制方程表达式为
(3)
(4)
式中:Q、M和Mγ分别表示变截面挠曲电纳米梁所受的剪力、弯矩和扭矩;w和φ分别表示变截面挠曲电纳米梁位移沿z轴的分量和截面相对于z轴的扭转角;ρ表示变截面挠曲电纳米梁的材料质量密度;NQ表示黏弹性基体对变截面挠曲电纳米梁的作用力,为简化计算,不考虑黏弹性基体的截面非均匀性,其表达式如下
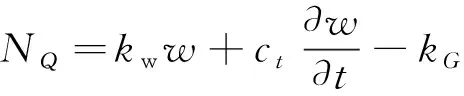
(5)
式中,kG、kw和ct分别表示visco-Pasternak黏弹性基体的剪切弹性模量、Winkler弹性模量和阻尼系数。
同时,为了确定变截面挠曲电纳米梁的力边界条件,基于非局部理论给出了变截面挠曲电纳米梁所受剪力Q、弯矩M和扭矩Mγ的表达式
(6)
(7)
(8)
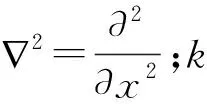
将式(6)~式(8)代入变截面挠曲电纳米梁的自由振动控制方程式(3)和式(4),考虑非局部效应的黏弹性基体中变截面挠曲电纳米梁的自由振动控制方程可表示为

(9)
kc44Axφ=[1-(e0a)2∇2]Z
(10)
式中
(11)
(12)
为了方便计算,引入以下变量参数
(13)
将以上变量参数代入式(9)和式(10),可将黏弹性基体中变截面挠曲电纳米梁的自由振动控制方程表示为
(14)
(15)
1.2 边界条件
为求解变截面挠曲电纳米梁的自由振动控制方程,下面给出几种典型边界条件
(1) 固支端边界条件
(16)
(2) 简支端边界条件

(17)
(3) 自由端边界条件

(18)
自由振动控制方程组式(14)和式(15)以及边界条件式(16)~式(18)共同构成了变截面挠曲电纳米梁振动特性分析的定解问题。由于自由振动控制方程组式(14)和式(15)为变系数微分方程,无法直接利用传递函数法进行求解。针对该问题,本文首先通过摄动法将变系数微分方程组式(14)和式(15)转化为常系数微分方程组,再利用传递函数法进行求解。
2 基于摄动理论的传递函数求解方法
2.1 传递函数法
将变截面挠曲电纳米梁的自由振动控制方程式(14)和式(15)的解设为
(19)
将式(19)代入式(14)和式(15),变截面挠曲电纳米梁的自由振动控制方程可表示为
(20)
(21)
定义状态向量
(22)
利用式(22)可将变截面挠曲电纳米梁的自由振动控制方程改写为状态方程的形式
(23)
类似地,将变截面挠曲电纳米梁的边界条件改写为状态方程的形式
Mη(0,ω)+Nη(1,ω)=0
(24)
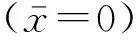
2.2 摄动法
由于变截面挠曲电纳米梁的自由振动状态方程式(23)为变系数微分方程组,不能直接利用传递函数法进行求解,可以利用摄动法将变系数微分方程组式(23)转化为常系数微分方程组,再利用传递函数法求得变截面挠曲电纳米梁的自由振动状态方程式(23)的解。
假设变截面挠曲电纳米梁的长度L远大于两端面高度之差h2-h1,因此前文定义的参数ε=(h2-h1)/L为无量纲小参数。根据摄动法原理,利用无量纲小参数ε对变截面挠曲电纳米梁的自由振动状态方程式(23)和边界条件状态方程式(24)进行参数分解,可得
ω=ω0+εω1+ε2ω2+…+εnωn
(25)
式中,ωj(j=0,1,2,…)是与固有频率ω相关的参数。文献[20]指出,一阶摄动解的精度已能满足实际计算需要,略去式(25)~式(29)中关于ε的高阶项可得
ω=ω0+εω1
(30)
(31)
(32)
M(ω)=M0(ω0)+εM1(ω0,ω1)
(33)
N(ω)=N0(ω0)+εN1(ω0,ω1)
(34)
将式(30)~式(34)代入变截面挠曲电纳米梁的自由振动状态方程式(23)和边界条件状态方程式(24),并略去关于ε的高阶项可得
(35)
(36)
通过以上变换可将变系数状态方程式(23)和式(24)转化为如式(35)和式(36)所示的常系数状态方程组,可利用传递函数法进行求解。
2.3 基于摄动理论的传递函数解法
根据摄动法原理和式(32),令ε=0可得F0(ω0)的表达式为
F0(ω0)=[Fmn|ε=0]6×6
(37)

(38)
根据传递函数法,变截面挠曲电纳米梁固有频率的零阶摄动值ω0可通过求解如下特征方程得到
det[M0(ω0)+N0(ω0)eF0(ω0)]=0
(39)
显然,变截面挠曲电纳米梁自由振动控制方程的零阶摄动值ω0为高为h1的等截面挠曲电Timoshenko纳米梁的固有频率,其相应振型为
(40)
式中,V0表示矩阵[M0(ω0)+N0(ω0)eF0(ω0)]的零特征值对应的特征向量。对于式(36),其通解为
(41)
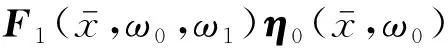
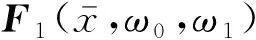
(42)
式中
(43)
然后,根据变截面挠曲电纳米梁的边界条件,选取对应的边界条件选择矩阵M和N,将式(42)代入式(36)中的第二个方程,可得
[M0(ω0)+N0(ω0)eF0(ω0)]R0+
ω1[M11V0+N0(ω0)eF0(ω0)V11(1)]+
ω1N11eF0(ω0)V0+N10eF0(ω0)V0+
M10V0+N0(ω0)eF0(ω0)V10(1)=0
(44)
根据矩阵的初等变换,有
M0(ω0)+N0(ω0)eF0(ω0)=[P][λ][P]-1
(45)
式中,[λ]和[P]分别表示矩阵[M0(ω0)+N0(ω0)·eF0(ω0)]的特征值组成的对角矩阵和与特征值相对应的特征向量组成的矩阵。将式(45)代入式(44)可得
[λ][P]-1R0+ω1D1+D0=0
(46)
式中
(47)
由式(39)可知,[λ]必有一个零特征值,由式(46)可得变截面挠曲电纳米梁的固有频率一阶摄动值为
(48)
根据式(30),变截面挠曲电纳米梁固有频率的一阶摄动解为
ω=ω0+εω1
(49)
同理,可以得到固有频率的高阶摄动解,在此不再赘述。
3 算例分析
本节首先通过与文献结果进行对比,验证所建模型和控制方程求解方法的正确性。在此基础上,再系统研究非局部效应、截面非均匀性、挠曲电系数和基体黏弹性对变截面挠曲电纳米梁振动特性的影响规律。如无特殊说明,变截面挠曲电纳米梁的几何参数设置如下:梁的长度L和宽度b分别为200 nm和25 nm,高度h1和h2分别为25 nm和12.5 nm;材料参数设置如下[20-22]:杨氏模量c11和剪切模量c44分别为131 GPa和42.9 GPa,横向挠曲电系数f3113和切向挠曲电系数f3131分别为5 V和1 V,质量密度ρ、倒介电常数α33和压电系数d31分别为6 020 kg/m3、0.79×108V·m/C和1.87×108V/m,visco-Pasternak黏弹性基体的Winkler弹性模量kw、剪切模量kG和阻尼系数ct分别为0.1 GPa/nm、0.25 GPa/nm和0.1 MPa·ns/nm。定义锥度系数c*=1-h2/h1以表征挠曲电纳米梁的截面非均匀性,显然c*=0表示等截面挠曲电纳米梁。
3.1 正确性验证
文献[19]研究微尺度下表面效应和挠曲电效应对等截面Timoshenko梁振动特性的影响规律,基于变分原理和哈密顿原理得到了挠曲电纳米梁的控制方程和边界条件,研究了均匀载荷下结构的静态弯曲和自由振动问题,但其忽略了挠曲电纳米梁的尺度效应和在实际工程应用中的工作环境,且未对变截面梁的振动特性进行研究。本节先忽略黏弹性基体和非局部效应的影响,通过和文献[19]对比简支边界条件下挠曲电纳米梁的前三阶无量纲固有频率,以验证本文模型和求解方法的正确性。
由表1可知,本文方法求得的等截面挠曲电纳米梁(c*=0)前三阶无量纲固有频率与文献[19]得到的等截面挠曲电纳米梁前三阶无量纲固有频率的误差最大仅为0.097 9%,验证了本文所建模型和求解方法的正确性。此外,表1给出了锥度系数c*分别为0.25和0.5时变截面挠曲电纳米梁的前三阶无量纲固有频率。

表1 S-S边界条件下挠曲电纳米梁的前三阶无量纲固有频率


表2 C-F边界条件下变截面SWCNT的前三阶固有频率/GHz
3.2 非局部参数的影响分析
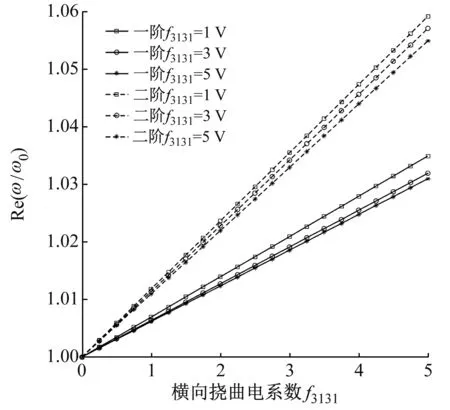
图2所示为不同边界条件下变截面挠曲电纳米梁前两阶固有频率频率比ωNL/ωL随非局部参数α的变化曲线,其中锥度系数c*取0.5,ωL表示非局部参数α为零时计算得到的结构固有频率值。由图2可知,C-F边界条件下变截面挠曲电纳米梁的一阶固有频率随着非局部参数α的增大而增大,而其余边界条件下变截面挠曲电纳米梁的一阶固有频率随着非局部参数的增大而减小,减小幅度随着边界连接刚度的增大而增大。各边界条件下变截面挠曲电纳米梁的二阶固有频率实部比和虚部比均随着非局部参数α的增大而减小,减小幅度同样随着边界连接刚度的增大而增大,各边界条件下变截面挠曲电纳米梁二阶固有频率受非局部参数α的影响由小至大的顺序为:C-F (a) 实部 图3所示为C-S边界条件下不同锥度系数c*对应的变截面挠曲电纳米梁一阶固有频率比ωNL/ωL随非局部参数α的变化曲线。由图3可知,随着锥度系数c*的增大,非局部参数α对挠曲电纳米梁一阶固有频率比ωNL/ωL实部和虚部的影响明显减小,当c*=0时,挠曲电纳米梁一阶固有频率比ωNL/ωL的变化幅度最大,而当c*=0.7时,挠曲电纳米梁一阶固有频率比ωNL/ωL的变化幅度最小。表明等截面挠曲电纳米梁受非局部参数α的影响最大,变截面特性能减小非局部参数α对挠曲电纳米梁的影响,且锥度系数c*越大,挠曲电纳米梁受非局部参数α的影响越小。 (a) 实部 图4所示为不同边界条件下挠曲电纳米梁前两阶固有频率比ω/ωc0随锥度系数c*的变化曲线,其中非局部参数α取0.1,ωc0表示锥度系数c*=0时计算得到的结构固有频率值。由图4可知,在C-F边界条件下,变截面挠曲电纳米梁的一阶固有频率大于等截面纳米梁的一阶固有频率,且随着锥度系数c*的增大呈线性增大;而其余边界条件下变截面挠曲电纳米梁的一阶固有频率小于等截面挠曲电纳米梁的一阶固有频率,且随着锥度系数c*的增大而减小,减小幅度随着边界连接刚度的增大而增大。变截面挠曲电纳米梁的二阶固有频率比ω/ωc0随着锥度系数c*的增大呈线性减小,且减小幅度同样随着边界连接刚度的增大而增大,不同边界下锥度系数c*对变截面挠曲电纳米梁二阶固有频率比ω/ωc0的影响由小至大的顺序为:C-F (a) 实部 图5所示为C-S边界条件下不同非局部参数α对应的变截面挠曲电纳米梁一阶固有频率比ω/ωc0随锥度系数c*的变化曲线。由图5可知,C-S边界条件下变截面挠曲电纳米梁的前两阶固有频率比ω/ωc0的减小幅度随着非局部参数α的增大而减小,当不考虑非局部效应(α=0)时,锥度系数c*对挠曲电纳米梁的振动特性影响最大,表明变截面挠曲电纳米梁的结构刚度随着锥度系数c*的增大而明显减小,且增大非局部参数α可以削弱结构对锥度系数c*的敏感程度。 (a) 实部 文献[23]指出,挠曲电系数对变截面纳米梁的固有频率虚部无影响作用,因此本文仅分析挠曲电系数对变截面挠曲电纳米梁固有频率比ω/ω0实部的影响规律,其中非局部参数α取0.1,锥度系数c*取0.5,ω0表示挠曲电系数(横向挠曲电系数f3113或切向挠曲电系数f3131)为零时计算得到的结构固有频率值。图6所示为C-S边界条件下变截面挠曲电纳米梁前两阶固有频率比ω/ω0实部随挠曲电系数的变化曲线。由图6(a)可知,变截面挠曲电纳米梁固有频率实部随着横向挠曲电系数f3113的增大线性增加,且增加幅度随着频率阶次的增大而增大,表明横向挠曲电系数f3113能增加变截面纳米梁的结构刚度;横向挠曲电系数f3113对变截面挠曲电纳米梁的影响幅度随着切向挠曲电系数f3131的增大而减小,表明增大切向挠曲电系数f3131可削弱结构对横向挠曲电系数f3113的敏感程度。由图6(b)可知,变截面挠曲电纳米梁固有频率实部随着切向挠曲电系数f3131的增大而减小,且减小幅度随着频率阶次的增大而增大,表明切向挠曲电系数f3131能削弱变截面纳米梁的结构刚度;切向挠曲电系数f3131对变截面挠曲电纳米梁的影响幅度随着横向挠曲电系数f3113增大而增大,表明增大横向挠曲电系数f3113可增加结构对切向挠曲电系数f3131的敏感程度。 (a) 不同切向挠曲电系数下横向挠曲电系数f3113对固有频率比ω/ω0实部的影响曲线 图7所示为C-S边界条件下不同锥度系数c*对应的挠曲电纳米梁一阶固有频率随黏弹性基体的阻尼系数ct的变化曲线。由图7可知,在C-S边界条件下,当黏弹性基体的阻尼系数ct小于不同锥度系数c*对应的临界阻尼系数ct_crit时,变截面挠曲电纳米梁固有频率的实部随着黏弹性基体阻尼系数ct的增大而减小,且临界阻尼系数ct_crit随着锥度系数c*的增大而减小;固有频率的虚部随着黏弹性基体阻尼系数ct的增大呈线性增大。当黏弹性基体的阻尼系数ct大于不同锥度系数c*对应的临界阻尼系数ct_crit时,变截面挠曲电纳米梁固有频率的实部为零,即不再发生往复振动;固有频率的虚部继续增加,增大趋势逐渐减小。 (a) 实部 本文以黏弹性基体中的Timoshenko纳米梁为研究对象,综合考虑了非局部效应、截面非均匀性、压电效应和挠曲电效应等因素,建立了黏弹性基体中的变截面挠曲电Timoshenko纳米梁的自由振动控制方程和边界条件,基于摄动理论给出了典型边界条件下变截面挠曲电纳米梁自由振动控制方程的传递函数求解方法,通过算例验证了所建模型和自由振动控制方程求解方法的正确性,并较系统地研究了非局部参数α、锥度系数c*、横向挠曲电系数f3113、切向挠曲电系数f3131和黏弹性基体的阻尼系数ct对挠曲电纳米梁振动特性的影响规律。主要结论如下: (1) C-F边界条件下变截面挠曲电纳米梁的一阶固有频率随着非局部参数α和锥度系数c*的增大而增大,高阶固有频率则随着非局部参数α和锥度系数c*的增大而减小。 (2) 非局部参数α对变截面挠曲电纳米梁固有频率的影响随着锥度系数c*的增大而减小;锥度系数c*对变截面挠曲电纳米梁固有频率的影响程度随着非局部参数α的增大而减小。 (3) 增大切向挠曲电系数f3131可削弱结构对横向挠曲电系数f3113的敏感程度;增大横向挠曲电系数f3113可增加结构对切向挠曲电系数f3131的敏感程度。 (4) 增大锥度系数c*能减小挠曲电纳米梁不发生往复振动对应的临界阻尼系数ct_crit。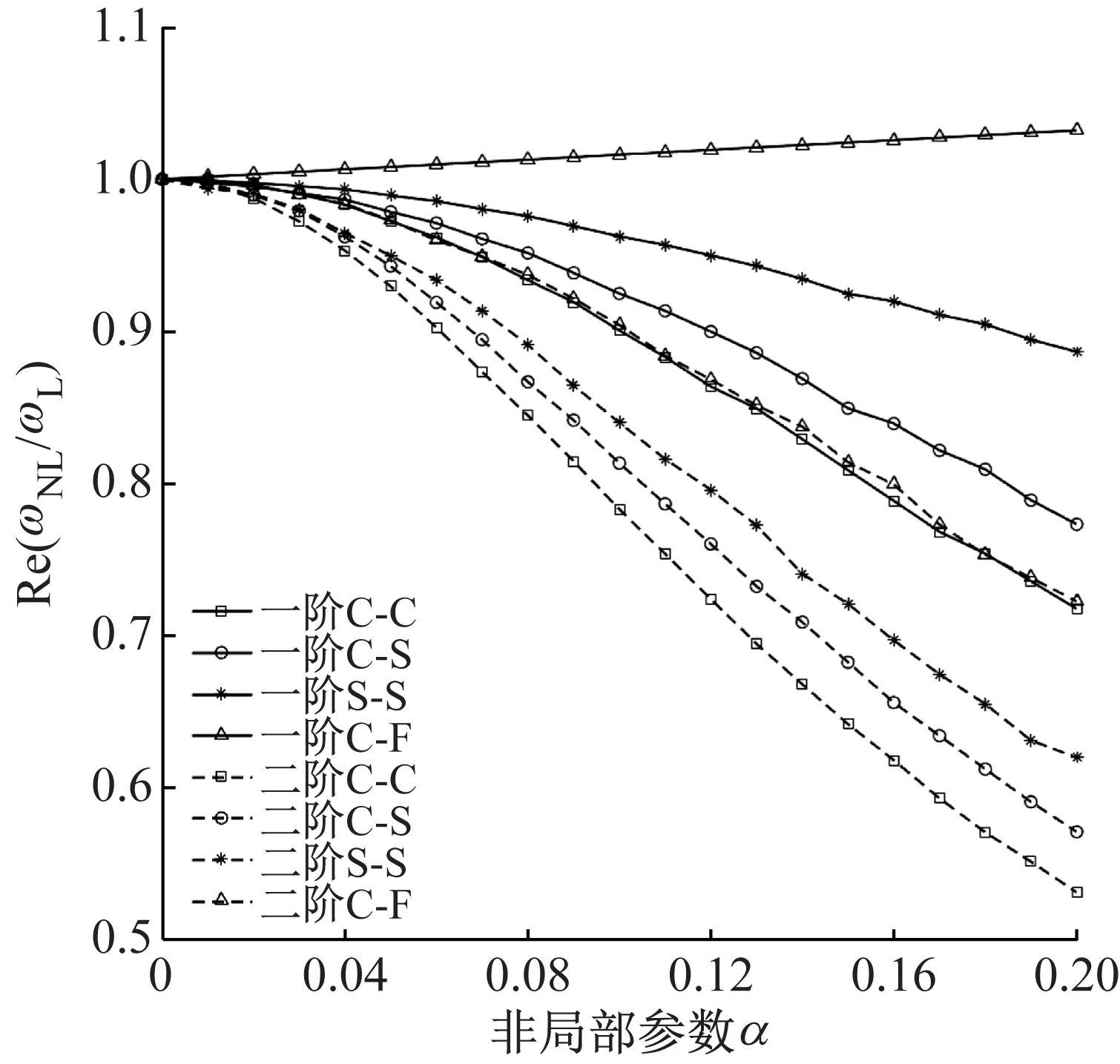

3.3 锥度系数的影响分析


3.4 挠曲电系数的影响分析
3.5 黏弹性基体的影响分析

4 结 论

