应用梯度连接层的层合电工钢梁螺栓结合部简化模型研究

关天赐， 王小鹏， 奚延辉

(西安交通大学 机械工程学院，西安 710049)

电工钢片具有良好的导磁性能，广泛应用于变压器、电机等电气设备中。为了减小涡流损耗，变压器铁心由电工钢片叠装而成。如何计及电工钢片层叠结构对变压器铁心动力学特性的影响，是准确建立铁心结构有限元仿真模型的关键。

在变压器铁心的装配过程中，电工钢片叠装后通过夹件与螺栓夹紧，电工钢片之间接触的表面为螺栓结合面[1]。由于变压器铁心是复杂的装配体，存在着大量的螺栓结合面，无法通过模态试验获得变压器铁心整体的模态参数。因此，无法对变压器铁心仿真模型进行参数识别，导致进行铁心整体静动态特性分析时产生很大的误差。如何对变压器铁心中电工钢片之间的螺栓结合部进行等效建模，是提高变压器铁心建模精度的关键。

国内外学者对于螺栓结合部的建模提出了多种方法，主要包括弹簧-质量法[2]、薄层单元法[3-5]、虚拟材料建模法[6-8]等。Wang等[9]在传统的弹簧质量模型中引入随应变率变化的弹性模量，提出了一种组合螺栓连接的刚度和强度预测模型。缪辉等[10]在拉杆转子的接触界面应用薄层单元模型，通过模态试验数据修正了薄层单元的弹性参数。薄层单元的厚度对计算结果影响较大，Desai等[11]研究表明薄层单元厚度与长度的比值在0.01～0.1。张学良等[12]提出基于横观各向同性材料的螺栓结合部等效建模方法，基于接触分形理论和结合部接触刚度分形模型推导了虚拟材料的弹性参数。Zhao等[13]提出了一种非线性虚拟材料对螺栓结合部进行建模，通过使用不均匀的表面接触应力确定非线性虚拟材料的参数。孙清超等[14]提出一种材料参数随位置坐标变化的梯度虚拟材料螺栓结合面等效模型。弹簧-质量法适用于简单结构的建模，在复杂结构中应用困难。薄层单元法可以应用于复杂结构中，但是在螺栓结合部增加了薄层单元，会改变结构的尺寸。等效虚拟材料模型在结合部接触刚度分形模型的基础上，应用接触分形理论推导虚拟材料弹性常数与密度。变压器铁心中电工钢片表面涂覆绝缘涂层，使其结合面特性复杂，用解析模型求解虚拟材料参数十分困难。

连接层模型是模拟螺栓结合部动态行为的一种新的方法。这一模型将螺栓连接的减刚度效应扩展到被连接结构的指定区域，称为连接层。与薄层单元法相比，连接层模型不改变结构的尺寸，连接层的厚度没有确定的取值。Shokrollahi等[15]在金属结构之间的螺栓结合部建立单连接层模型，Adel等[16]在金属与复合材料结构之间的螺栓结合部建立双连接层模型，分别通过试验结果对连接层的弹性参数进行了修正。但是，文献中将连接层模型定义为均匀材料，没有考虑螺栓结合部压强分布不均匀的特点。

针对电工钢片间的螺栓结合部导致变压器铁心无法准确建模的问题，本文提出了一种考虑结合面压强分布不均匀的梯度连接层模型。根据螺栓结合部压强分布，推导了梯度连接层弹性参数与结合部接触压强的关系表达式。以层合电工钢梁试件为研究对象，通过试验模态与计算模态对比获得试件的等效材料参数。在此基础上，两根层合电工钢梁由螺栓连接，在螺栓结合部建立梯度连接层模型。通过螺栓连接层合电工钢梁试验模态与计算模态对比，以对应试验频率和计算频率的差值最小化为目标函数，应用遗传算法修正了梯度连接层的弹性参数。

1 梯度连接层模型

Adel等提出一种模拟螺栓结合部的连接层模型，如图1所示。该模型将螺栓连接的减刚度效应扩展到两个被连接结构的指定区域，称为连接层。在实际建模中，将材料相同的两个被连接件的连接层作为整体进行计算。连接层的厚度没有确定的取值，密度与被连接件相同，结构的总体质量和尺寸不变。通过改变连接层的弹性性能，可以改变结构的局部刚度，从而在线性范围内研究螺栓连接对结构的影响。连接层模型能够应用在复杂结构的有限元仿真模型中，从而提高计算精度。

图1 螺栓结合部连接层模型

连接层模型基于螺栓连接的减刚度效应，螺栓结合部压强分布不均匀会导致不同区域减刚度效应不同。文献[15-16]中提出的连接层模型无法准确表示螺栓结合部压强分布不均匀的特点。因此，本文根据结合部压强分布特点，将连接层模型划分为3层，提出一种考虑结合部压强分布不均匀的梯度连接层模型，如图2所示。

图2 螺栓结合部梯度连接层模型

首先，需要定义梯度连接层的本构关系。由于梯度连接层模型使用了被连接结构的部分区域，为了方便附加到有限元程序中，连接层与相邻结构的单元类型相同，均为三维实体单元。梯度连接层单元的刚度矩阵K如式(1)所示。

(1)

式中：C为材料的弹性矩阵；B为单元几何矩阵；V为单元体积。

本文研究的层合电工钢梁是一种复合结构，因此将梯度连接层定义为正交各向异性材料，本构方程如式(2)所示。

(2)

式中：σi和εi(i=x,y,z)为材料3个主轴方向的正应力和正应变；τij和γij(i=x,y,z;j=x,y,z;i≠j)为材料的切应力和切应变；Gij(i=x,y,z;j=x,y,z;i≠j)为材料的剪切模量；Cij(i=x,y,z;j=x,y,z)为刚度矩阵系数，由材料3个主轴方向的杨氏模量与泊松比确定，如式(3)～(9)所示

(3)

(4)

(5)

(6)

(7)

(8)

(9)

式中：Ei(i=x,y,z)为材料3个主轴方向的弹性模量；νij(i=x,y,z;j=x,y,z;i≠j)为材料的泊松比。其中，弹性常数存在以下关系

νijEj=νjiEi(i=x,y,z;j=x,y,z;i≠j)

(10)

因此，正交各向异性材料具有9个独立的弹性参数。

螺栓结合面压强分布不均匀，压强分布可以简化为空心圆锥体[17]，压强沿径向逐渐减小，如图3所示。结合面的压强分布如式(11)～(13)所示

(11)

图3 螺栓结合部压强分布示意图

(12)

rm=rb+h·tanα

(13)

式中：P(r)为结合部不同位置的压强；Pmax为结合部压强最大值；Fb为螺栓预紧力；ri为螺栓孔半径；rm为螺栓结合部压强分布末端半径；rb为螺栓头半径；h为被连接件厚度；α为螺栓头和结合部压强分布末端连线与螺栓中心线的夹角。

假设在均匀压力下单位面积结合面的法向刚度Kn和切向刚度Kτ如式(14)～(15)所示[18]

Kn=αn·P(r)βn

(14)

Kτ=ατ·P(r)βτ

(15)

式中:αn、βn为结合部法向特性参数；ατ、βτ为结合部切向特性参数。

根据材料力学中弹性模量和剪切模量与法向刚度和切向刚度的的关系，推导出梯度连接层的弹性模量和剪切模量与压强的关系如式(16)～(17)所示。

(16)

(17)

式中：E(r)为梯度连接层不同位置的弹性模量；G(r)为梯度连接层不同位置的剪切模量；A为梯度连接层xy平面内的面积；h为梯度连接层z轴方向上的厚度。

本文中将梯度连接层划分为3个分层，每个分层的压强取为平均接触压强，见图2。梯度连接层为正交各向异性材料，由于螺栓连接的压力沿z方向，根据文献[12]，假设梯度连接层3个分层x方向的弹性模量相等，y方向的弹性模量相等，xy方向的剪切模量相等，z方向的弹性模量与xz、yz方向的剪切模量与接触压强关系如式(16)～(17)所示，3个方向泊松比与被连接结构相同。梯度连接层的材料参数与螺栓预紧力、表面粗糙度与螺栓结合面材料等参数有关。

2 层合电工钢梁螺栓结合部简化建模

2.1 层合电工钢梁的设计与参数识别

由于电工钢片厚度通常小于0.5 mm，单独两片间的螺栓结合面研究比较困难。因此，本文首先制作了层合电工钢梁试件，如图4所示。试件由10片公称厚度0.3 mm的电工钢片沿Z轴堆叠并通过胶黏层粘接在一起，试件质量为478.7 g。电工钢片的几何尺寸如图5所示。由于电工钢片的厚度公差为±0.015 mm，通过千分尺测量试件60个点的厚度，试件沿Z轴方向的厚度为3 mm，公差为±0.020 mm。由于试件没有确定的材料参数，无法进行螺栓结合部的等效建模研究。因此，本文首先通过试验模态与计算模态对比识别层合电工钢梁的等效材料参数。

图4 层合电工钢梁试件

图5 电工钢片几何尺寸

本文在自由-自由边界条件下对层合电工钢梁进行模态试验，如图6所示。通过冲击锤(5800B3，DYTRAN)对试件施加脉冲激励，试件表面等距布置23个测点。将三轴加速度传感器(3333A2，DYTRAN)安装在试件表面的A1点。由于加速度传感器质量远小于试件质量，忽略加速度传感器对试验的影响。每个测点重复测量4次，存储平均频响函数与相干函数。通过数据分析仪(m+p VibPilot)记录试验数据并进行模态试验分析，获得试件前6阶试验频率如表1所示。从表1中可以看出，参数识别后层合电工钢梁仿真计算的前4阶固有频率与试验频率之间的误差均小于1%，并且准确地预测了未参与识别过程的第5和第6阶固有频率，说明识别后的材料参数可以用于层合电工钢梁的仿真计算。

图6 试件模态试验设置

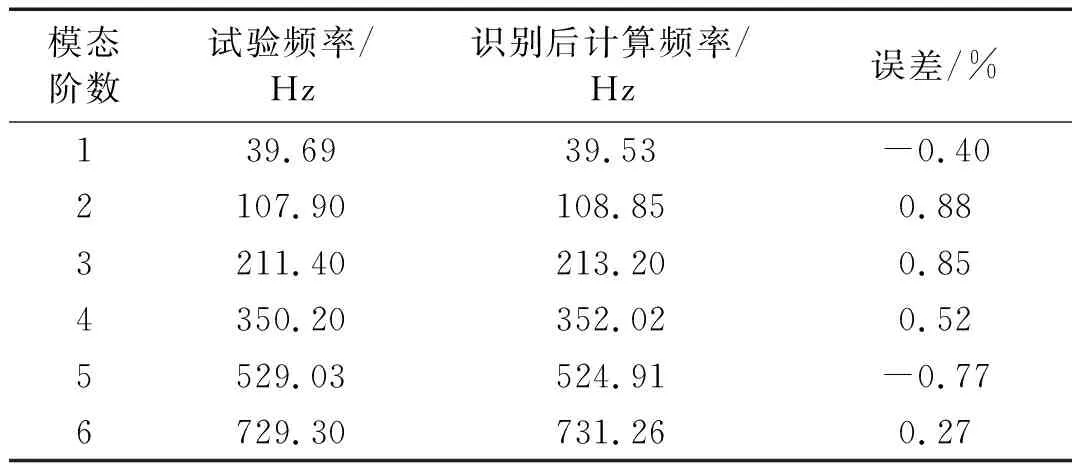
表1 试件试验频率与识别后计算频率

层合电工钢梁结构具有各向异性，根据文献[19]，层合电工钢梁在x与y轴方向性能基本相同，可近似认为试件具有横观各向同性。因此，将层合电工钢梁的材料定义为正交各向异性材料，材料参数之间的关系如式(18)～(21)所示

(18)

(19)

(20)

(21)

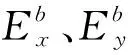
为了识别层合电工钢梁的等效材料参数， 通过有限元计算与模态试验获得的固有频率差值最小化来确定试件材料参数，目标函数如式(22)所示

(22)

(23)

(24)

(25)

(26)

表2 试件材料参数初始值及变化范围

通过遗传算法对层合电工钢梁的材料参数进行识别[20-21]。层合电工钢梁材料参数的识别值如表3所示。

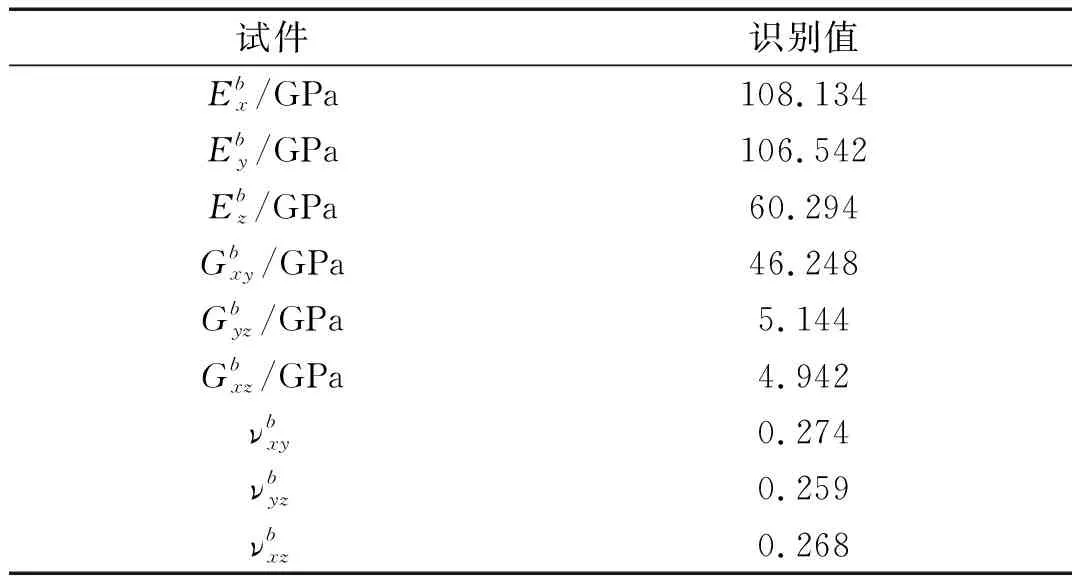
表3 试件材料参数识别值

2.2 螺栓连接层合电工钢梁模态试验

在识别后试件材料参数的基础上，进一步研究层合电工钢梁螺栓结合部简化模型。将两根本文中设计的层合电工钢梁通过M10螺栓连接，两根层合电工钢梁尺寸相同，连接区域长度为60 mm，整个连接结构几何尺寸如图7所示。

非布司他治疗2型糖尿病肾病合并高尿酸血症的临床观察…………………………………………………… 张春林等（4）：501

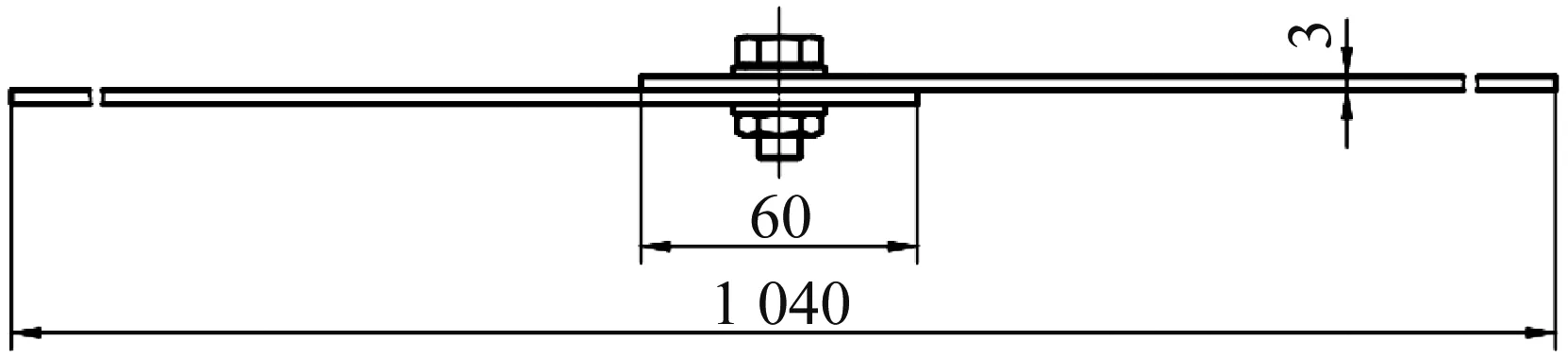
图7 螺栓连接层合电工钢梁几何尺寸

为了获得螺栓连接层合电工钢梁的模态参数，在自由-自由边界条件下对螺栓连接层合电工钢梁进行模态试验，如图8所示。根据实际生产中变压器铁心的装配压强，施加的螺栓预紧扭矩为1.0 N·m。采用冲击锤(5800B3，DYTRAN)对试件施加脉冲激励，试件表面布置43个测点。将三轴加速度传感器(3333A2，DYTRAN)安装在试件表面的A2点。每个测点重复测量4次，存储平均频响函数与相干函数。

图8 螺栓连接层合电工钢梁模态试验设置

通过数据分析仪(m+p VibPilot)记录试验数据并进行模态试验分析，获得螺栓连接层合电工钢梁的频响函数如图9所示，前8阶试验振型如图10所示，前8阶固有频率如表4所示。

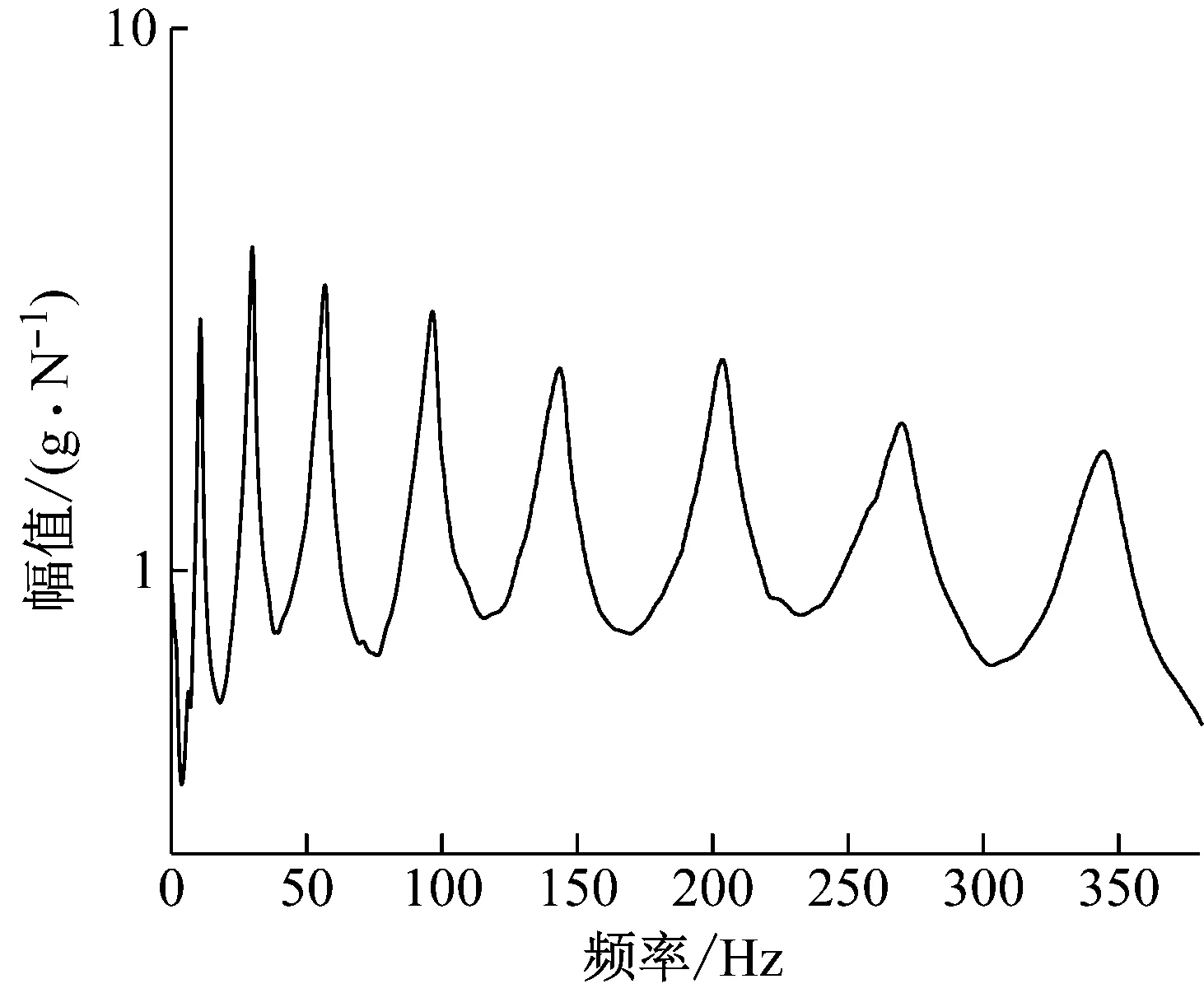
图9 螺栓连接层合电工钢梁的频率响应函数

图10 螺栓连接层合电工钢梁的试验振型图

表4 螺栓连接层合电工钢梁试验频率与初始计算频率

2.3 螺栓连接层合电工钢梁模态仿真

通过ANSYS有限元软件对螺栓连接层合电工钢梁进行模态仿真，有限元模型如图11所示。两根层合电工钢梁之间建立梯度连接层模型并定义绑定接触，分层1和2的直径分别为24和36 mm，螺栓、螺母与垫圈(32 g)简化为集中点质量。连接层的厚度没有确定取值，文献[11]研究表明当连接薄层长度与厚度比值为10～100时能取得较为准确的结果。因此，在梯度连接层的长度与厚度比值范围内，为了方便计算，本文将梯度连接层厚度设置为1 mm。

图11 螺栓连接层合电工钢梁的有限元模型

初始仿真中，层合电工钢梁与梯度连接层应用表3中识别后的材料参数。仿真模型中层合电工钢梁与梯度连接层均使用20个节点的三维单元(solid186)，包括12 911个单元与70 116个节点。在仿真模型的y轴方向定义零位移约束，该约束可以避免模型的横向弯曲(y-x平面内)与扭转模态，保证在改变设计参数时不改变振型的阶数。仿真计算后螺栓连接层合电工钢梁的前8阶振型如图12所示。从图12可以看出，仿真计算的模型前8阶振型与图10中模态试验分析得到的前8阶振型一致。

(a) 第1阶振型

在振型一致的前提下，仿真模型计算的初始前8阶固有频率见表4。从表中可以看出，螺栓连接层合电工钢梁的前8阶试验频率均小于初始计算频率，说明结合面的刚度小于结构其它部分的刚度，仿真时定义绑定接触与实际误差较大。在研究变压器铁心的动态特性时，不考虑电工钢片间的接触，建立整体铁心模型与实际误差较大。此外，奇数阶模态频率误差大于偶数阶模态频率误差，因为偶数阶模态中螺栓结合部被置于节点位置，不参与结构动力响应。但是，对于奇数阶模态，螺栓结合部位于振动的峰值处，会导致结合面发生微小滑移与分离，从而误差较大。因此，需要对梯度连接层的弹性参数进行修正。

3 梯度连接层参数修正

螺栓连接层合电工钢梁的前8阶试验频率与计算频率误差较大，需要使用试验结果修正梯度连接层的材料参数。本文中参数修正方法的流程图如图13所示，其基本步骤如下：

图13 梯度连接层参数修正流程图

(1) 在有限元软件ANSYS中对螺栓连接层合电工钢梁进行建模，并在其螺栓结合部建立梯度连接层模型，仿真计算得到结构初始计算频率和模态振型；

(3) 设置约束条件，基于遗传算法对梯度连接层的弹性参数进行修正；

(4) 目标函数满足终止条件后，得到修正后的梯度连接层弹性参数。

由于螺栓连接的压力沿z方向，根据文献[12]，假设梯度连接层3个分层x方向的弹性模量相等，y方向的弹性模量相等，xy方向的剪切模量相等，z方向的弹性模量与xz、yz方向的剪切模量与接触压强关系如式(16)～(17)所示，3个方向泊松比与被连接结构相同。梯度连接层的密度与被连接结构相同。因此，在参数修正过程中梯度连接层3个分层弹性参数的关系如式(27)～(32)所示

(27)

(28)

(29)

(30)

(31)

(32)

目标函数与式(22)相同，梯度连接层材料参数的初始值及变化范围如表5所示。通过遗传算法对梯度连接层的材料参数进行修正，第5～8阶固有频率用来验证修正后梯度连接层材料参数的准确性。目标函数迭代收敛过程如图14所示。从图中可看出，经过18次迭代后收敛，每次迭代计算20个设计点。

表5 梯度连接层材料参数初始值及变化范围

图14 目标函数迭代收敛曲线

修正后梯度连接层的等效材料参数如表6所示，螺栓连接层合电工钢梁模态仿真计算的固有频率如表7所示。从表7中可以看出，修正后螺栓连接层合电工钢梁的前4阶计算频率与试验频率之间的误差均小于1%，未参与修正过程的第5～8阶固有频率误差同样小于1%，说明应用修正后的梯度连接层模型能够提高螺栓连接层合电工钢梁的建模精度。

表6 梯度连接层材料参数修正值

表7 螺栓连接层合电工钢梁修正后计算频率

从表6中可以看出，修正后梯度连接层3个分层的弹性参数与初始值相比，下降幅度较大。分层1在x、y和z方向的弹性模量分别下降了24倍、29倍和22倍，在xy、yz和xz方向的剪切模量分别下降了66倍、20倍和42倍，说明结合面的刚度小于结构其它部分的刚度。梯度连接层3个分层的弹性参数满足结合部压强分布关系，说明结合部刚度分布不均匀。通过应用修正后的梯度连接层模型，能够在线性范围内对螺栓连接层合电工钢梁的结合部进行等效建模。

4 结 论

(1) 本文提出了一种考虑螺栓结合部压强分布不均匀的梯度连接层模型。以层合电工钢梁为研究对象，通过试验模态与计算模态对比修正了层合电工钢梁的等效材料参数，修正后试件前6阶计算频率与试验频率的误差均小于1%。

(2) 在层合电工钢梁的螺栓结合部建立梯度连接层模型。通过螺栓连接层合电工钢梁的试验模态与计算模态对比，应用遗传算法修正了梯度连接层的弹性参数。在振型一致的前提下，修正后对应固有频率的误差在1%以内，说明修正后的梯度连接层模型能准确反映层合电工钢梁螺栓结合部的接触性能。

(3) 修正后梯度连接层不同分层弹性参数满足结合部压强分布关系并且均小于初始值，说明修正后的梯度连接层参数能够反映结合部刚度减小与压强分布不均匀的物理特性。通过在变压器铁心中应用修正后的梯度连接层模型，能够提高计算精度。