用于次同步振荡分析的直驱风电场等值模型

赵伟哲，崔 成，严干贵，何 昊，熊华强，王俊茜，翟文超

（1.国网江西电力科学研究院，江西 南昌 330006；2.东北电力大学，吉林 吉林 132000；3.国网江西省电力有限公司，江西 南昌 330006）

0 引言

近年来，大力发展风电资源是推进能源转型和应对环境挑战的重要途径[1-3]。截至到2020 年6 月底，我国风电累计装机容量2.17 亿千瓦。预计到2050 年风电装机容量将达24 亿千瓦[4-6]，呈现快速发展态势。

由于风电场的大规模接入，电力系统呈现高比例新能源发电与高比例电子电子化设备（电子电子化设备是新能源发电并网的源网接口装置）的特征，即“双高”电力系统，其运行安全面临诸多新问题。如2011 年，河北沽源地区双馈风电场（Doubly-fed Induction Generators，DFIG）与固定串补相互作用引发的次同步振荡（sub-synchronous oscillation，SSO）[7]；2015 年，新疆哈密地区直驱风电场（direct-drive Permanent Magnet Synchronous Generator，PMSG）与弱交流电网相互作用引发的次/超同步振荡[8]。

国内外学者基于特征值法、时域仿真法、阻抗分析法等展开研究。文献[9-11]建立了PMSG 机群低运行工况下接入弱交流系统的线性化模型，同样分析了电网强度、运行工况、风机台数、控制参数等因素对振荡特性的影响。研究结果表明：（1）该类振荡在电网中难以找到固有的振荡模态，属于PMSG 控制主导的电气振荡；（2）电网强度、运行工况、并网台数、电流内环比例系数的增加，有利于系统稳定。（3）振荡频率与同步发电组（Synchronous Generator，SG）轴系扭振频率接近时，可能会激发其轴系扭振。

理想情况下，建立每台风电机组的详细电磁暂态模型能够完整、准确地反映系统振荡特性。而实际风电场具有风机数量多、运行工况分散、经集电线路连接等特点，搭建风电场全阶模型存在阶数高、仿真运行速度慢等问题，不利于理论分析[12]。文献[13]针对风电场动态等效模型的建立，推导了风电场线性化模型的相似变换，探讨对并网风电场进行单机等值的理论条件。文献[14]推导得到风电机群单机等值模型，在风电机群内各WTG 型号相同且运行状态相似的前提下，单机等值模型可有效衡量机群动态特性。然而，文献[4]-[14]的研究并未考虑风电场运行工况、集电线路的差异性，风电机组之间会存在相互作用，可能影响系统的动态特性。此时，单机等值方法无法分析机组间的振荡机理。因此，构建恰当的主导振荡特性保持等值模型具有重要的研究意义。

不同于现有研究，本文针对PMSG 风电场次同步振荡的等值建模问题，围绕电流内环主导的直驱风电场次同步振荡问题，参考SG 并联建模研究工作，基于相似变换原理建立主导振荡特性保持的等值模型，分析系统电流内环控制参数、电网强度等因素对系统次同步振荡的影响。在PSCAD 中搭建时域仿真模型，验证了理论分析的正确性与有效性。

1 相似变换原理在SG建模中的应用

1970 年，美国Mohave 电厂的两台SG 在做扭振模式测量时发现了双峰现象[15-17]，即在扭振自然频率附近出现2 个频率幅值相近的谐波分量。此后，国外学者展开了对并联SG 振荡特性的研究，得到的结论如下：

1）Robert T.H.A.等人认为当N台运行状态相同的SG 接入公共母线时，将各个SG 轴系都用M个集中质量块来表示，则系统共有N×M个振荡模式，其中振荡特性相同的模式称为共模，振荡特性对应特征根线性无关的模式称之为异模[12]；

2）Jennings G.D.等人提出单机等值的方法来研究系统的SSO 稳定性，等值过程为：将单机容量扩大为各个机组容量的2 倍，即可使同型两机系统等值为1 台机。比对等值系统与原始系统的振荡模式发现两者特征值轨迹基本一致，证实了方法的可行性[15]。

2006 年，文献[17]在此研究基础上进一步从数学上证明了相似变换原理应用于SG 等值建模的可行性，具体推导过程如下：

以2 台SG 并联为例研究等值原则，其中2 台SG 是同型机组且结构对称、参数相同，两机并联数学模型为：

式中：XS和XL分别为SG 状态变量和电网的状态变量；AS和AL分别为SG 和电网的各自内部状态变量之间的耦合关系；BU和BI分别为SG 与电网之间的电压和电流的耦合关系；iSd和iSq分别为SG 输出电流的直轴和交轴分量；uSd和uSq为SG 输出电压的直轴和交轴分量；下标1，2 表示发电机编号。

闭环系统的状态方程为：

构造一个可逆矩阵：

式中：IS，IL为单位矩阵，维数分别与AS，AL相同。

对式（2）中状态矩阵ASG进行相似变换，得：

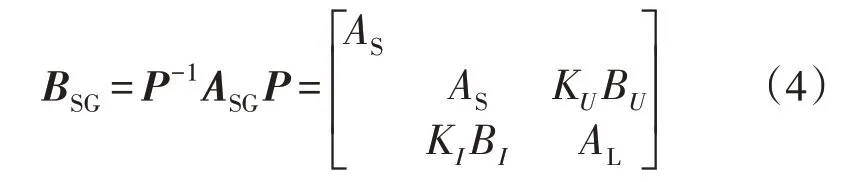
由式（4）可知，矩阵ASG与BSG为相似矩阵，具有相同特征值，且全部由BSG中2 个子矩阵的特征值构成。其中KU和KI分别为电压耦合和电流耦合关系系数，乘积为并联台数。

由式（4）可知：（1）两机并联系统可分解为2 个独立的子系统，第一部分子系统相当于单台SG 与电压和频率恒定的公共母线连接，称之为单机对无穷大公共母线系统，第二部分子系统相当于在单台SG 的输出电流中乘以系数2 后，通过原输电线路与无穷大母线连接，称为修正的单机对网络系统，两机并联等值模型如图1 所示。图1 中Δixy、Δvxy分别表示SG 与外部系统之间的电流和电压变化量；（2）分别计算2 个子系统特征值，即可获取系统全部特征值信息，达到简化计算的目的。

图1 两机并联系统Fig.1 Two-machine parallel equivalent model

文献[18-19]进一步分析了单机对无穷大公共母线特征值Λ11对应的模态只存在于机组1，2 间，幅值相同相位相反，为冗余模式；修正的单机对网络系统特征值Λ22，Λ33对应的模态存在与所有状态变量中，且在机组1，2 间幅值相位相同，为公共模式，在此不再赘述。

2 风电场的等值建模

依托相似变换原理，进一步围绕电流内环主导的PMSG 风电场多机并联系统，研究其等值建模问题，完善建模体系，验证风电场等值模型的适用性。

2.1 直驱风电场数学模型

风电场并网的拓扑结构如图2 所示，经0.62 kV/35 kV 机端变压器汇入集电系统，出口处经35 kV/220 kV 升压变压器连接至交流电网。图2 中各PMSG 机组容量均为1.5 MW，系统总阻抗为Z，交流电网强度一般用短路比（Short-Circuit Ratio，SCR）表征，即交流电网短路容量Sac与风电场额定容量SN之比[19-20]，如式（5）所示。

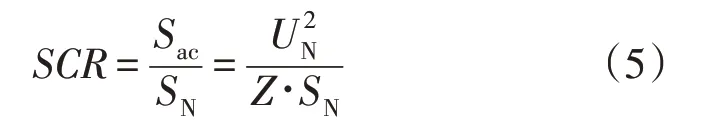
图2 PMSG风电场并联接入弱交流系统Fig.2 D-PMSG-based wind farm integrating into weak AC system

PMSG 的控制策略如图3 所示。图3 中，ωr，ωg为转子角速度和电网同步旋转角速度；Udc为电容电压；Lf，Ls为滤波电感和永磁同步机电感；ψf为永磁同步机磁链；id，iq为变流器输出电流d轴和q轴分量；下标s表示机侧变流器，g 表示机侧变流器，下标ref 表示参考值。其中机侧变流器采用定子电流isdref=0 的dq解耦控制策略，将转子角速度ωr与给角速度参考值ωrref比较，差值经PI 环输出即为q轴电流参考值，dq轴电流经电流内环PI 调节，形成变流器机侧输出电压Us，经PWM 调制，输出脉冲信号控制机侧变流器[21-23]。

图3 直驱风机控制框图Fig.3 Control block diagram of direct-drive wind turbine

网侧变流器采用电网电压矢量定向控制，将直流侧电压udc与给定母线电压参考值udcref比较，差值经PI 环输出即为d轴电流参考值，dq轴电流经电流内环PI 调节，形成变流器网侧输出电压Ug，经PWM 调制，输出脉冲信号控制网侧变流器[24]。

由图2 和图3 可知，PMSG 风电机组转子运动方程、机侧变流器主电路的数学模型如式（6）、式（7）所示：

式中：TJ为惯性时间常数；Tm为机械转矩；Te为电磁转矩。

式中：Ld和Lq分别为等值电感的dq轴分量；ψsd和ψsq分别为定子绕组磁通的dq轴分量；Rs表示定子绕组电阻；id和iq分别为网侧变流器输出电流的dq轴分量。

网侧变流器主电路的数学模型为：

式中：Ud和Uq分别为电流控制器输出的调制电压dq轴分量；Utd和Utq为同步坐标系下网侧变流器端电压。

结合式（6）—式（8）以及PMSG 控制策略，得到单台PMSG 状态方程为：

式中：XS_PMSG和XL_PMSG分别为PMSG 状态变量和电网的状态变量；AS_PMSG和AL_PMSG为PMSG 和电网的各自内部状态变量之间的耦合关系；BU_PMSG和BI_PMSG分别为PMSG 与电网之间的电压和电流的耦合关系。

2.2 风电场模型

以N台同型PMSG 风电机组并联系统为例，建立PMSG 风电场的状态矩阵AN为：

依照公式(3)构建N 机可逆矩PN，对状态矩阵AN进行相进行变换，得：

由式（11）可知，N机并联系统的状态矩阵AN的特征值可以由两部分组成。第一部分子系统[AS，…，AS]等值为单个PMSG 风电场接入无穷大母线系统，反映了PMSG 风电机组间的振荡模式。第二部分[AS，k1BU；k2BI，AL]相当于修正的单个PMSG 风电场并网系统，其中k1，k2分别为电压耦合BU与电流耦合BI的系数，系数乘积为n，第二部分表示PMSG 风电场与电网之间的振荡模式。

当PMSG 为同型机组，且具有对称结构、相同的参数和负载特性时，等值模型大大降低了系统阶数；等价后，系统阶数从18×n+4 减少到18 阶（单台PMSG 接入无限大母线）+22 阶（修改后的单台PMSG 接入电网）。

PMSG 风电场通常由数百个风电机组成，受实际风电场中各风电机组地理位置存在差异性等影响，PMSG 风电场难以保证在相同的工况下运行，不能满足等值条件。此时，可结合K-means 分群方法，将具有相似工况的PMSG 风电场分为一群，分群后的各PMSG 风电场大致满足相同的运行条件，从而每群能够等值为两个单独单元[25-26]；否则，不可进行等值。PMSG 风电场多机并联等值模型，如图4 所示。

图4 N机并联系统Fig.4 Parallel system of N-machine

3 等值模型验证

为验证等值模型的有效性，分别搭建两机并联系统、50 机并联系统以及100 机并联系统，对比全阶模型与等值模型的特征根的差异性。

3.1 两台PMSG风电场并联模型验证

构建两台PMSG 风电机组并联系统，参数、运行工况一致，直驱风机运行风速为4 m/s，电流内环比例控制参数Kp为0.23，电网强度SCR 为3 时，3种模型计算得到的特征值（无量纲）如表1 所示。由表1 可知，修正的单机对网络系统计算出来的公共模式、单机对无穷大母线系统计算出来的冗余模式与全阶模型计算出来的模式基本一致。

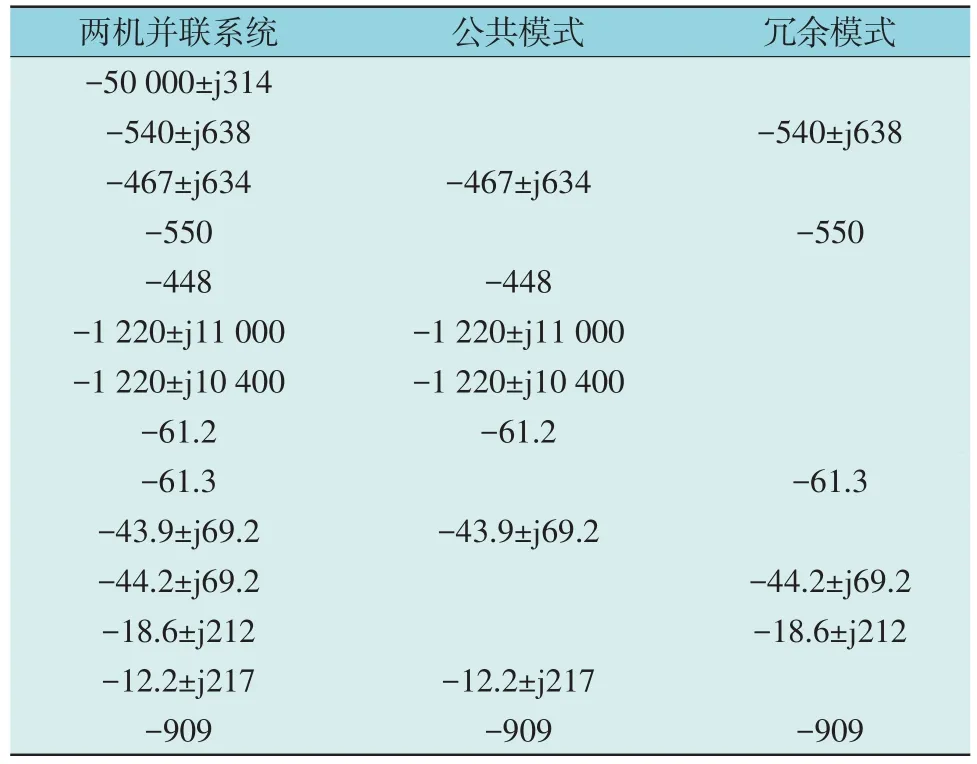
表1 系统特征值结果Table 1 System eigenvalue calculated by three models

3.2 50台PMSG风电场并联模型验证

搭建如图5 所示的50 台PMSG 风电机组并联接入弱交流系统模型。各台PMSG 风电机组的风速数据为吉林省某风电场实际风速数据，选择某一时刻的实际风速数据作为输入风速。

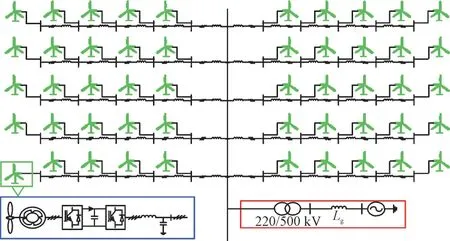
图5 50台PMSG风电场并网模型Fig.5 Model of 50-PMSG based wind farm integration into weak AC system

基于K-means 聚类算法将50 台风电机组按照运行工况进行分群，选取PMSG 风电场分群数为3群，具体分群结果如表2 所示。

表2 50台风机并联分群结果Table 2 Grouping results of parallel 50-wind turbine m/s

根据式（12）计算分群等值风速veq，具体等值风速分别为4.212 m/s，5.452 m/s 和6.938 m/s，式中vi为各机组实际运行风速。即：

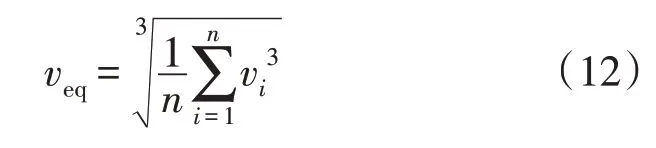
分别构建50 台PMSG 风电机组并联的全阶线性化模型、等值修正的3 台PMSG 风电机组接入弱电网线性化模型、等值3 台PMSG 风电机组接入无穷大电网线性化模型，其中详细模型共（18×50+4=904）阶，修正的3 机对网络模型（18×3+4=58）阶，3机对无穷大电网模型54 阶。当SCR 为1.4、PMSG风电机组电流内环比例控制参数Kp 为0.23 时，50台PMSG 风电机组详细模型和等值模型的部分特征值如表3 所示。

表3 系统部分特征值结果Table 3 Partial eigenvalue of detailed model and equivalent model of 50-PMSG

由表3 可知：（1）该算例条件下，50 台PMSG风电机组并联系统分群等值后，修正的3 机对网络系统对应的模式为公共模式，50 机系统中其他模式为冗余模式；（2）等值模型公共模式特征值实部误差率小于5.7%，虚部误差率小于0.07%，其中主导振荡特征值实部误差率为5.7 %，虚部误差率为0.04%；（3）详细模型时域仿真时间2.5 s，实际运行时间为30 min，等值模型实际运行时间为11 s，等值方法大大缩短了仿真时间。

由于实际风电并网工程中风机台数、风机分布位置可能存在差异，并网数量及每台风机所连接的集电线路长度可能不同。故分两种情况对比全阶模型与等值模型的差异性，验证等值模型的有效性。

1）不考虑风机台数和集电线路的差异性，电流内环比例控制参数Kp从0.2～0.3 变化时，详细模型和修正的3 机对网络模型的主导振荡特征值如图6（a）所示。

2）考虑集电网络影响是，摄动集电线路长度变化，基于等功率损耗原则，计算分群等值后的3 群集电线路长度。电流内环比例控制参数Kp从0.2～0.3 变化时，详细模型和修正的3 机对网络模型的主导振荡特征值如图6（b）所示。

图6 详细模型与等值模型对比Fig.6 Comparison of detailed model and equivalent model

由图6 可知，PMSG 风电机组电流内环比例控制参数变化时，两个模型特征值的变化趋势基本一致，等值模型可有效地保持详细模型的主导振荡特性。二者都有效地表明随着电流内环控制系数的增加，特征值向左半平面迁移，不利于系统发生次同步振荡。

3.3 100台PMSG风电场并联模型验证

进一步扩大系统规模，搭建100 台PMSG 风电机组并联接入弱交流系统模型。各台PMSG 风电机组的风速数据为吉林省某风电场实际风速数据。

基于K-means 聚类算法将100 台风电机组按照运行工况进行分群，选取PMSG 风电场分群数为5 群，具体分群结果如表4 所示。

表4 100台风机并联分群结果Table 4 Grouping results of parallel 100-wind turbine m/s

100 台详细并联模型共（10×100+4=1 004）阶，修正的5 机对网络模型（10×5+4=54）阶，5 机对无穷大电网模型50 阶；当SCR 为1.4、PMSG 风电机组电流内环比例控制参数Kp为0.23 时，100 台PMSG风电机组详细模型和等值模型的部分特征值如表5所示。

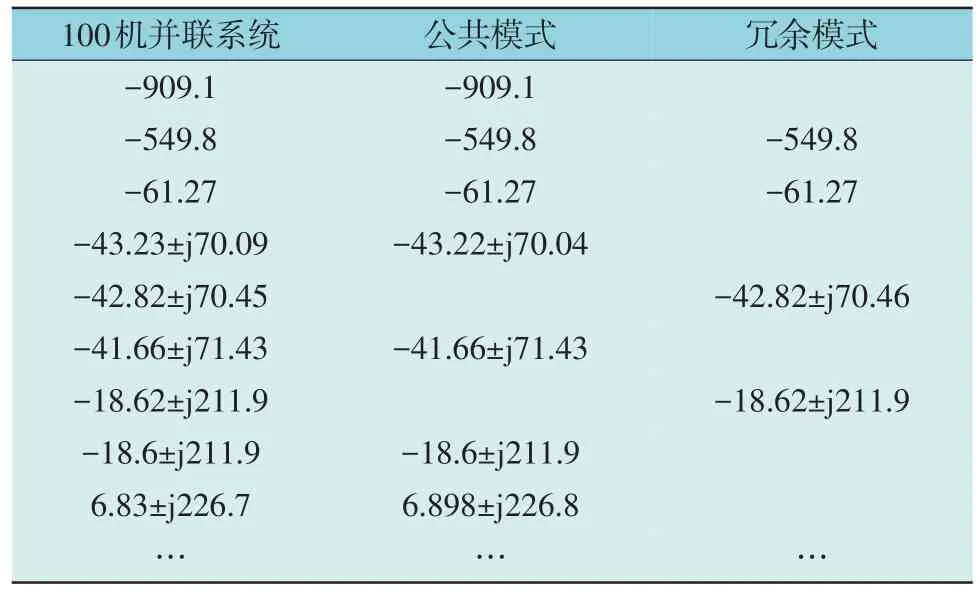
表5 系统部分特征值结果Table 5 Partial eigenvalue of detailed model and equivalent model of 100-PMSG

在该算例条件下，100 机详细模型分群等值模型主导振荡特征根实部误差率为2.31%，虚部误差率为0.04%。

4 结语

本文基于相似变换原理建立了PMSG 风电场主导振荡特性保持的等值模型，通过在两机并联系统、50 机并联系统以及100 机并联系统中，对比全阶模型与等值模型主导特征值的差异性，验证了等值模型的有效性。当考虑风电场并网台数和集电线路之间的差异时，等值模型的精度基本保持不变。