基于无源性理论的光伏储能型准Z源并网逆变器控制方法研究

鲍克勤，陈海燕，程启明，吴浩强

（上海电力大学自动化工程学院，上海 200090）

0 引言

光伏发电系统具有节能减排、成本廉价、安全性高等特点，正逐步代替传统的轻化石燃料，有望成为未来新能源发展的主力[1]。随着光伏材料和功率转换器的发展，光伏发电系统也在不断发展[2-4]。功率转换器是整个光伏发电系统的重要组成部分，它将光伏产生的能量转化为负载和网侧所需的电源。传统的两级并网功率转换器存在结构复杂、成本较高的缺点[5-7]。Z 源逆变器（Z-Source Inverter，ZSI）或准Z 源逆变器（quasi ZSI，qZSI）虽能够简化系统，但无法解决光伏电池输出电流的突变[7-9]。本文选取的储能型qZSI 可在系统中集成一个应对负载需求的储能装置，这样不仅有助于光伏电池储存多余的能量或补足能量，还可以平滑电网注入功率的波动[11-13]。

目前有很多国内外学者对储能型qZSI 在光伏系统中应用的稳定性以及优化控制展开研究。文献[14]提出储能型qZSI 拓扑的设计方案以及储能阻抗网络变换器的控制方案，实现储能型qZSI 光伏系统的最大功率点跟踪（Maximum Power Point Tracking，MPPT）和并网控制。文献[15]针对滑模控制的稳态误差问题，提出储能单元电流调节的积分滑模控制方法，提高系统对输入输出扰动的鲁棒性，但其控制器结构更加复杂，滑模系数也不易确定。文献[16]提出的模型预测控制减少了传感器的数量，但是当系统参数不准确时对系统性能会有影响，且开关频率不固定。文献[14-16]的研究虽然已经将一些非线性控制方法用于qZSI 中，且与比例微分（Proportion Integration，PI）控制相比响应速度有所提升，但其控制方法较为复杂，且对于外部扰动较为敏感。

无源控制（Passivity Based Control，PBC）是一种非线性控制方法，它具备设计简单、响应快速、全局稳定性高、无奇异点等优点。目前，无源性控制理论已被应用于逆变器等电力电子器件的控制上，并取得了理想的控制效果[17-19]。本文首次将无源性控制方法引入储能型qZSI 的控制中。相比于传统PI 控制器，根据无源性理论设计的无源控制器能够实现系统的全局稳定性和无奇异点，其突出优势在于能够很好地平滑电网注入功率的波动，且控制系统的结构简单、控制参数更少、响应更快，整体控制效果更好。

1 储能型qZSI光伏并网系统

1.1 系统工作原理

本文所研究的储能型qZSI 光伏并网系统结构框图如图1 所示。该系统主要由光伏（Photovoltaic，PV）发电单元、储能型准Z 源单元以及电网单元组成。

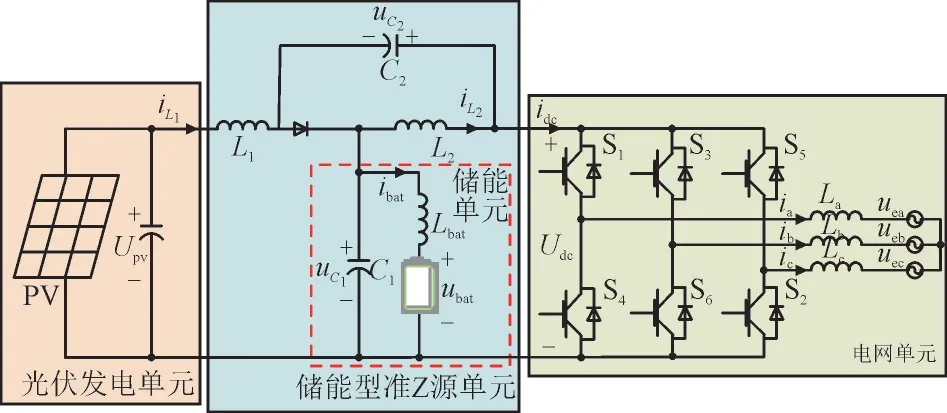
图1 储能型qZSI光伏并网系统结构框图Fig.1 Structure energy storage qZSI PV gridconnected system

图1 中，iL1，iL2分别为储能型qZSI 网络电感L1，L2的电流，uC1，uC2分别为储能型qZSI 网络电容C1，C2的电压，Lbat，ibat，ubat分别为电池的电感、电流和电压，Upv为光伏输入电压，Udc，idc分别为直流链电压和电流，La，Lb，Lc分别为a，b，c 3 相的滤波电感，uea，ueb，uec分别为a，b，c 3 相的电压，ia，ib，ic分别为a，b，c 3 相的电流，S1—S6为逆变器开关。

储能型qZSI 直通状态和非直通状态的等效电路如图2 所示。

图2 储能型qZSI直通状态和非直通状态的等效电路Fig.2 Equivalent circuit of shoot-through state and nonshoot-through state of energy storage qZSI

根据图2 直通状态和非直通状态下的等效电路，使用状态空间平均法，可得开关周期内储能型qZSI 的状态平均方程如式（1）所示：

式中：D为直通占空比。

1.2 状态平均模型

在电网三相逆变桥电压平衡的情况下，根据逆变器的工作原理结合图1，得到两相d，q轴下的数学模型如式（2）所示：

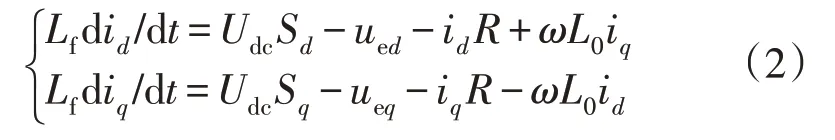
式中：Lf为滤波电感；Sd，Sq分别为开关函数Sk在d，q轴下的分量；ued，ueq分别为d，q轴下交流侧电压；id，iq分别为d，q轴下并网电流；R为线路电阻；ω为角频率；L0为线路电感。

非直通状态下，根据三相逆变桥的开关函数推出逆变器桥臂输入电流idc如式（3）所示：

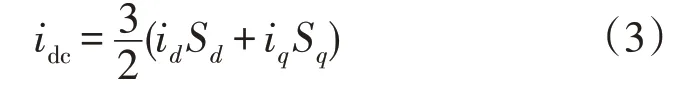
结合式（1）和式（2）得到储能型qZSI 并网逆变器的状态平均模型如式（4）所示：

式中：假定C=C1=C2为直流侧电容的容量；假定L=L1=L2为直流侧电感的容量。

1.3 系统工作模态

根据PV 输出功率Ppv与qZSI 向网侧输出的有功功率参考值Poutref两者之间的大小关系，得到储能型qZSI 光伏并网系统的5 种工作模态，如表1 所示。

表1 储能型qZSI光伏并网系统的5种工作模态Table 1 Five working modes for qZSI PV gridconnected system with energy storage

2 储能型qZSI的控制器设计

无源控制基于能量控制的思路，通过选取和确定合适的能量存储函数，使系统在满足全局渐近稳定的条件下达到期望的控制效果。本文在设计储能型qZSI 无源控制器过程中，为增加系统在光伏功率波动、网侧功率变化下的鲁棒性和能量耗散速度，采用阻尼注入法加快系统的响应速度，使系统结构简单、易于控制，具备全局稳定性和无奇异点[20-22]。

2.1 储能型qZSI的E-L模型

根据欧拉—拉格朗日（Euler-Lagrange，E-L）方程，将式（4）转换成符合无源控制要求的E-L 模型如式（5）所示：

式中：M为正定对角矩阵；为系统状态向量的一阶导；J为反对称矩阵，即J=-JT，其反映逆变器系统内部互联结构；x为系统状态向量；α为反映系统耗散特性的对称矩阵；u为系统输入向量。

2.2 控制系统无源性和稳定性证明

如果存在一个正定函数Q（x）以及半正定且连续可微的能量存储函数H（x），可以得到耗散不等式，则系统是严格无源的，其严格无源不等式如式（6）所示：

针对本文储能型qZSI 光伏并网系统，设能量存储函数为H(x)=xTMx/2，结合式（5）可得：

由于J=-JT，因此存储函数中xTJx=0 ；令y=x，Q(x)=xTαx，可推出其满足式（6）的耗散不等式，即储能型qZSI 是严格无源的。根据无源控制思想：具备严格无源性的系统一定可以采用无源控制，且控制系统是稳定的。从而证明储能型qZSI 无源控制系统的稳定性[23-24]。

2.3 无源控制器设计

设定误差变量xeg=x-x*，其中x*为系统状态的期望平衡点，如式（8）所示：

式中：idref，iqref，uC1ref，uC2ref，iL1ref，iL2ref分别为id，iq，uC1，uC2，iL1，iL2的参考值。

选取无源系统的控制规律如式（9）所示：

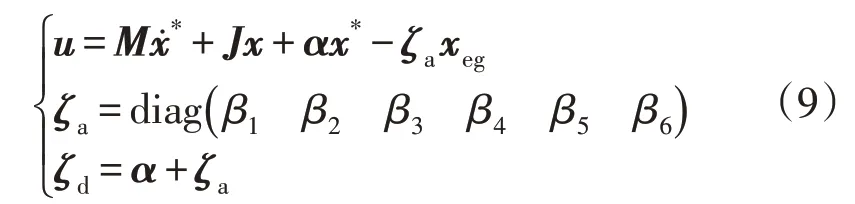
联立式（5）和式（9），可以得到开关函数如图3所示。图3 为能使电流解耦的储能型qZSI 无源控制器的控制规律。

图3 开关函数Fig.3 Diagram showing switching functions

假设本文使用的电路元件均为理想器件且忽略功率损耗，根据功率守恒定律，储能型qZSI 光伏并网系统功率关系如式（11）所示：

式中：Ppv，Pbat，Pout分别为光伏发电功率、蓄电池输出功率、逆变器向网侧输出的有功功率。

由式（11）可知，当调整Ppv，Pbat，Pout中任何2 个功率，则第3 个功率将自行补足功率缺额，使得等式恒成立。且qZSI 通过调节直通占空比信号和调制比，来调度光伏和逆变器的输出功率。因此，推导出系统控制思想为：采用无源控制调节脉冲宽度调制（Pulse Width Modulation，PWM）信号，使得Pout跟随参考值Poutref，通过调节直通占空比信号，使光伏发电输出功率处在最大功率点，则Pbat根据功率守恒方程会自动补足功率缺额。

储能型qZSI 无源控制器结构框图如图4 所示。图4 中Upvref，ibatref分别为Upv，ibat的参考值。Qoutref为无功功率参考值。蓄电池功率控制单元采用的是蓄电池电流作为内环、功率作为外环的控制策略，其中内环需把网侧三相电流转换到d，q轴的直流分量进行控制，实现蓄电池充放电控制。光伏功率控制单元由MPPT 算法实现[25-26]。

他是一个不知道自己有什么弱点的人，比如他说话时结巴，可他自己不知道，或者说他从来没有承认过这一点，他的妻子萍萍是一个漂亮的女人，留着很长的头发，不过大多数时间她都是把头发盘起来，她知道自己的脖子很长很不错，她有时候穿上竖领的衣服，她的脖子被遮住了大半以后，反而更加美妙了，那衣服的竖领就像是花瓣一样。

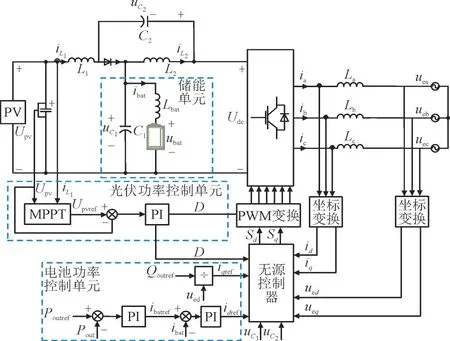
图4 储能型qZSI无源控制器结构框图Fig.4 Structure of energy storage qZSI PBC system

3 仿真分析

为验证本文所提无源控制策略的有效性和优越性，搭建了如图4 中的储能型qZSI 无源控制系统，其系统实验参数如表2 所示。

表2 系统实验参数Table 2 Experimental parameters of energy storage qZSI PBC system

为全面验证所提控制策略应对各种运行工况下的优势，本文模拟了日间光照强度变化运行、夜间无光照运行、网侧功率变化运行3 种工况下整个系统的运行情况，并将本文所提无源控制与PI 控制进行实验比较分析。

3.1 日间光照强度变化运行工况

在日间有光照情况下，系统可在工作模态1—3之间相互切换。模态3 为不充电不放电状态，此时储能型qZSI 不工作，故在此不做赘述。

设置初始光照强度为800 Lx，第0.5 s 时，光照强度从800 Lx 阶跃到400 Lx，逆变器向网侧输出的有功功率参考值Poutref为3×104W。图5 为日间光照强度变化时各参数变化曲线，图5 中电池的荷电状态（State of Charge，SOC），其物理量符号用Soc 表示。

图5 日间光照强度变化时各参数变化曲线Fig.5 Variation curves of each parameter when changes in daytime light intensity

结合表1 和图5 可知，第0.5 s 前系统工作在模态1 充电状态，第0.5 s 后光伏发电系统工作在模态2 放电状态，系统始终满足功率守恒条件。相比于PI 控制，无源控制得到的Pout能基本稳定在3×104W，且系统具有响应速度快，波形稳定，动态性能更好等优点。因此，储能型qZSI 在无源控制下能够通过蓄电池充放，更好地补偿光强变化引起的功率波动。

3.2 夜间无光照运行工况

在夜晚无光照情况下Ppv=0，此时系统可在模态4 或模态5 下工作。图6 为模态4 功率曲线。

图6 模态4功率曲线Fig.6 Power curves for mode 4

当深夜电价处于谷段且用电需求下降时，此时电价较为实惠，可以用来给电池充电。图7 为模态5 功率曲线。由图7 可知，系统开始运行时，以1×104W输出功率向电池充电，第0.5 s 时，由于夜晚用电需求量降低，电网以3×104W 输出功率给电池充电。忽略功率损耗可视Pbat=Pout。因此，蓄电池在无源控制下可以平稳高效地从电网吸收能量。

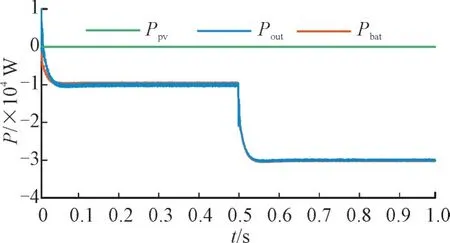
图7 模态5功率曲线Fig.7 Power curves for mode 5

3.3 网侧功率变化运行工况

为验证系统通过逆变器向网侧输出有功功率参考值响应情况，将光照强度保持在800 Lx，Poutref为6.5×104W，第0.5 s 时，Poutref阶跃到3×104W。图8 为网侧功率变化时功率、蓄电池SOC 曲线。

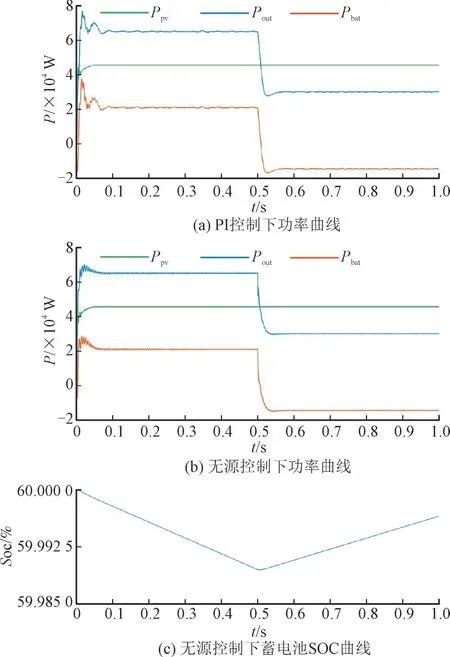
图8 网侧功率变化时功率、蓄电池SOC曲线Fig.8 SOC curves of power and battery when changes in power at network side

结合表1 和图8 可知，相比PI 控制，无源控制下逆变器向网侧输出的有功功率Pout跟随参考值Poutref的速度更快，且能较快稳定。在Poutref开始阶跃变化前，由于Ppv＜Pout，光伏不能足够给网侧提供能量，因此蓄电池开始放电，以弥补网侧所需能量差额，系统工作在模态2；Poutref发生阶跃变化后，Ppv＞Pout，光伏向网侧输送能量，并将剩余的能量供应给电池充电，系统工作在模态1。Poutref阶跃前后系统始终满足功率守恒条件，因此储能型qZSI 在无源控制下能够通过蓄电池充放电很好地补偿网侧输出功率变化引起的系统功率缺额。

通过3 种工况实验结果分析可知，不管是在哪种运行工况下，本文无源控制系统均能够保持系统稳定运行，并且能够在5 种工作模态之间快速平滑切换。相比于传统PI 控制，本文所提无源控制方法的超调量更小、波形更为平滑、调节时间更短、稳态误差更小、鲁棒性更强，也即其动态性能和静态性能都更加优越。此外，无源控制相对于PI 控制，控制参数更少，能够更快对控制参数进行整定。

4 结论

本文提出一种储能型qZSI 的非线性无源控制方法，论证了储能型qZSI 的稳定性，建立了储能型qZSI 的E—L 模型，推导了其无源控制规律，并设计出储能型qZSI 的无源控制器。仿真分析表明，本文所提方法具有可行性和优越性，得到如下结论：

1）本文设计的无源控制与传统PI 控制相比，具备可调参数较少、超调更小、动态性能更为良好等优势。

2）无源控制策略下，蓄电池能够吸收或释放能量，做到充、放电的灵活切换。

3）储能型qZSI 光伏并网系统可以通过无源控制策略获得更好的动态性能，使系统中的蓄电池对光强变化及网侧功率变化快速响应，并能够自动弥补功率的缺额。