含SVG直驱风电场降阶模型与宽频振荡抑制措施研究
王 阔
(北京大学,北京 100191)
0 引言
构建以新能源为主体的新型电力系统,新能源装机占比逐年升高,对电力系统安全稳定运行提出诸多挑战,新能源场站并网产生的宽频振荡问题[1-5]便是其中之一。2012 年起华北地区沽源风电场曾发生多起次同步谐振现象[6-7]。2015 年新疆哈密地区北部以直驱风机为主力机型的风电场发生次/超同步振荡现象,导致风电场附近火电机组因轴系扭振保护相继动作跳闸,同时造成该地区电网频率下降[8-9]。
为了提升电压支撑能力,已投入运行的新能源场站和正在筹划建设的新能源场站均会配置静止无功发生器(Static Var Generator,SVG)。新能源场站调试和正常运行发现SVG 发生振荡现象。文献[10]提出SVG 与双馈风机发生次同步振荡系限幅饱和引起的切换型振荡。文献[11-12]提出SVG 可与直驱风机发生次同步振荡,但未分析影响振荡的因素及如何抑制振荡。因此,研究含SVG 新能源场站宽频振荡影响因素和抑制措施具有实际意义。
本文采用模态分析法分析含SVG 直驱风电场宽频振荡特性,采用直驱风电机组阻尼控制器和SVG 阻尼控制器协调设计来抑制含SVG 直驱风电场中宽频振荡。首先建立了含SVG 直驱风电场的线性化模型;分析了含SVG 风电场并网系统中可能存在宽频振荡;提出了含SVG 直驱风电场并网电力系统宽频振荡阻尼控制器设计方法,最后验证了所提方法的有效性。
1 含SVG直驱风电场降阶模型
含SVG 直驱风电场的结构如图1 所示,永磁同步发电机(Permanent Magnet Synchronous Generator,PMSG)经过箱变和集电线路连接到风电场内35 kV母线上,SVG 直接并联在35 kV 母线,多段35 kV 母线再经过主变连接在风电场出口母线W 上。其中,PMSGLj_i为35 kV 母线j下第i台PMSG;SVGj为35 kV 母线j下SVG;PL1_pi,QL1_pi,VL1_pi和XL1_dwi分别为35 kV 母线1 下第i台PMSG 的有功、无功、机端电压和送出线路电抗。
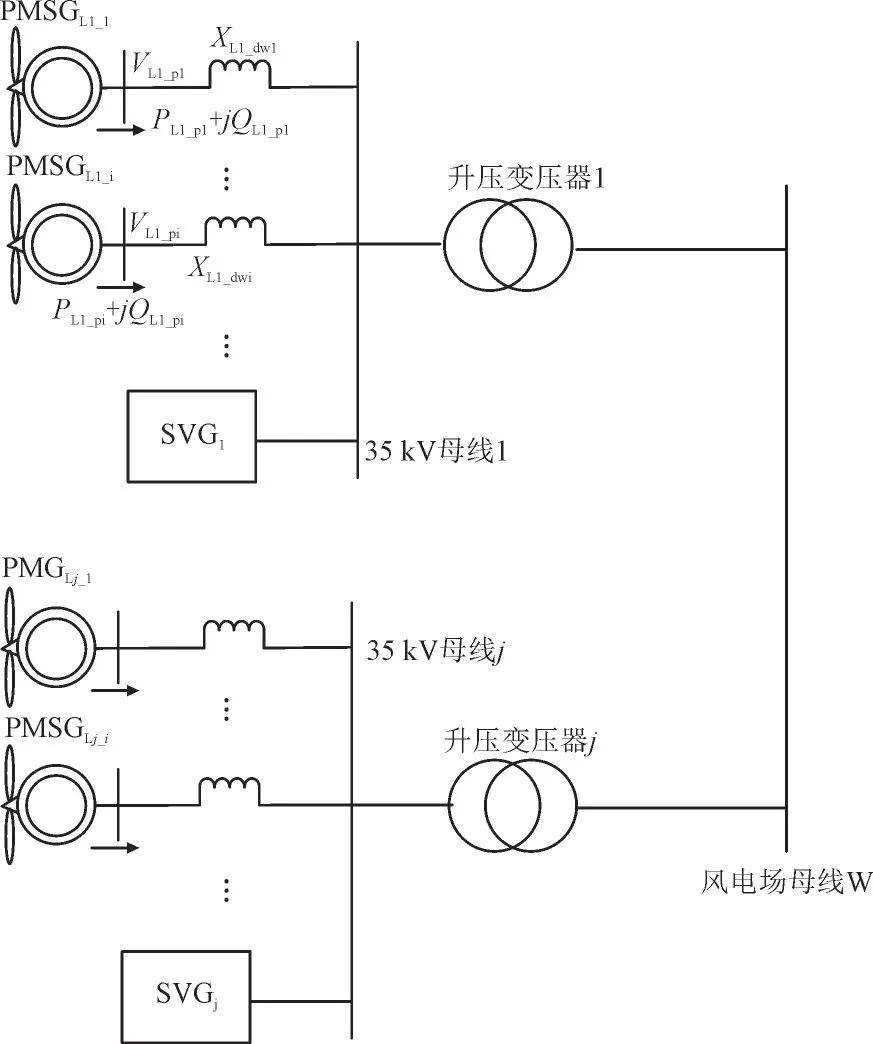
图1 含SVG直驱风电场结构示意图Fig.1 Structure of PMSG-based wind farm with SVG
1.1 PMSG模型
图2 为直驱风电机组的模型[13-16],其中,MSC 为机侧换流器;GSC 为网侧换流器;Pm和Qm分别为永磁同步发电机提供的机械有功和无功;Pw和Qw分别为直驱风机发出的电磁有功和无功;Vdc为直流电压;Xf1为滤波电抗;为直驱风机的端电压。

图2 直驱风电机组模型Fig.2 Model of PMSG wind turbines
PMSG 的状态空间方程[17]为:

式中:Δ 为变量在稳定运行点邻域内的微增量;XPMSG为PMSG 的状态变量;UPMSG为PMSG 的控制变量;YPMSG为PMSG 的输出变量;APMSG为PMSG的状态矩阵;BPMSG为PMSG 的控制矩阵;CPMSG为PMSG 的输出矩阵。
1.2 SVG模型
SVG 通过发生容性无功或感性无功调节风电场母线电压,主要结构如图3 所示[18]。其中,Cdc为直流电容;Vdc为直流电容电压;idc为直流电流;Lsvg为滤波器电感;isvgd,isvgq为SVG 输出电流的dq轴分量;Vsvgd,Vsvgq为SVG 端口电压的dq轴分量;Vsvgcd,Vsvgcq为SVG 换流器输出电压的dq轴分量。

图3 SVG模型Fig.3 Model of SVG
如图3 所示,SVG 换流器的外环控制回路主要为定无功功率控制和定直流电压控制,内环控制回路主要为定电流控制。
根据图3,SVG 直流电容的微分方程为:

SVG 滤波器的微分方程为:

式中:ωsvg为参考坐标系的旋转角速度。
SVG 的锁相环结构如图4 所示。其中,Vsvga,Vsvgb,Vsvgc分别为SVG 的abc 三相电压;Vsvgd,Vsvgq为SVG 的d轴电压和q轴电压;ω0,ωsvg分别为额定转速和SVG 转速;θsvg_pll为SVG 锁相角;s为拉普拉斯算子。
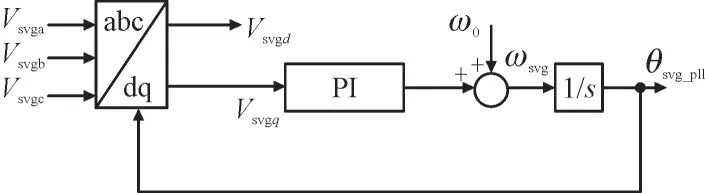
图4 SVG锁相环结构示意图Fig.4 Structure of phase-locked loop in SVG
根据图4,SVG 锁相环的微分方程为:
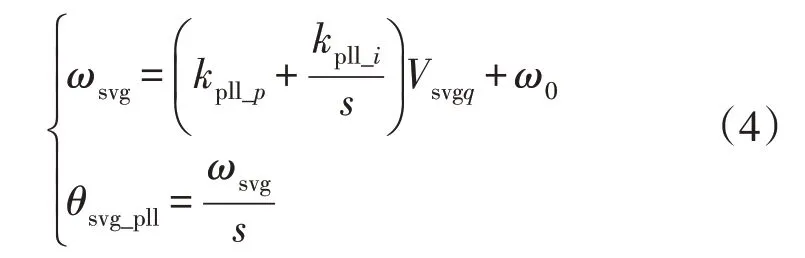
式中:kpll_p,kpll_i为锁相环控制器的PI 控制参数;θsvg_pll为锁相环输出的相角;ω0为电网同步旋转角速度。
根据图3 和式(2)—式(4),SVG 的状态空间方程为:
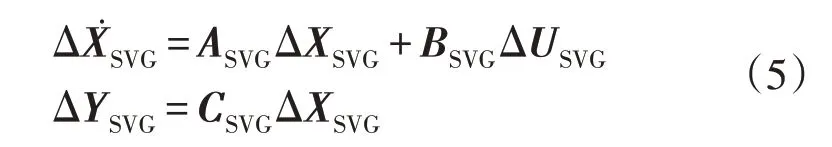
式中:XSVG为SVG 的状态变量;USVG为SVG 的控制变量;YSVG为SVG 的输出变量;ASVG为SVG 的状态矩阵;BSVG为SVG 的控制矩阵;CSVG为SVG 的输出矩阵。
1.3 含SVG直驱风电场并网系统模型
假设直驱风电场包含M段35 kV 母线,每段母线均配置1 台SVG,第1 段35 kV 母线到第M段母线分别包含N1,N2,…NM台PMSG。
含SVG 直驱风电场并网系统的状态空间模型可表示为:
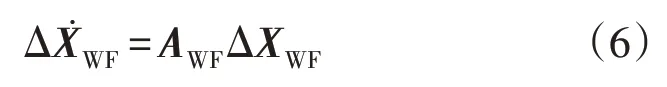
式中:XWF为含SVG 直驱风电场并网系统状态变量;AWF为含SVG 直驱风电场并网系统状态矩阵。
1.4 含SVG直驱风电场并网系统降阶模型
式(1)中PMSG 状态空间方程共16 阶,式(5)中SVG 状态空间方程共9 阶,假设交流系统包含K阶状态方程,则1.3 中含SVG 直驱风电场并网系统包含(N1+N2+…+NM)×16+M×9+K阶状态方程。当直驱风电场中35 kV 母线分段较多、PMSG 台数较多时,状态矩阵AWF呈高维度。计算AWF的特征值及特征向量,将要占用相当多的CPU 资源和时间。
为了节省计算资源,减小含SVG 直驱风电场并网系统特征值和特征向量计算难度,本文提出一种含SVG 直驱风电场并网系统降阶状态空间模型[19]。
假设含SVG 直驱风电场中连接到同一段35 kV母线下的PMSG 生产厂家、型号和参数完全相同,并且每段35 kV 母线下的SVG 生产厂家、型号和参数也完全相同,则式(6)中状态矩阵AWF可表示为:
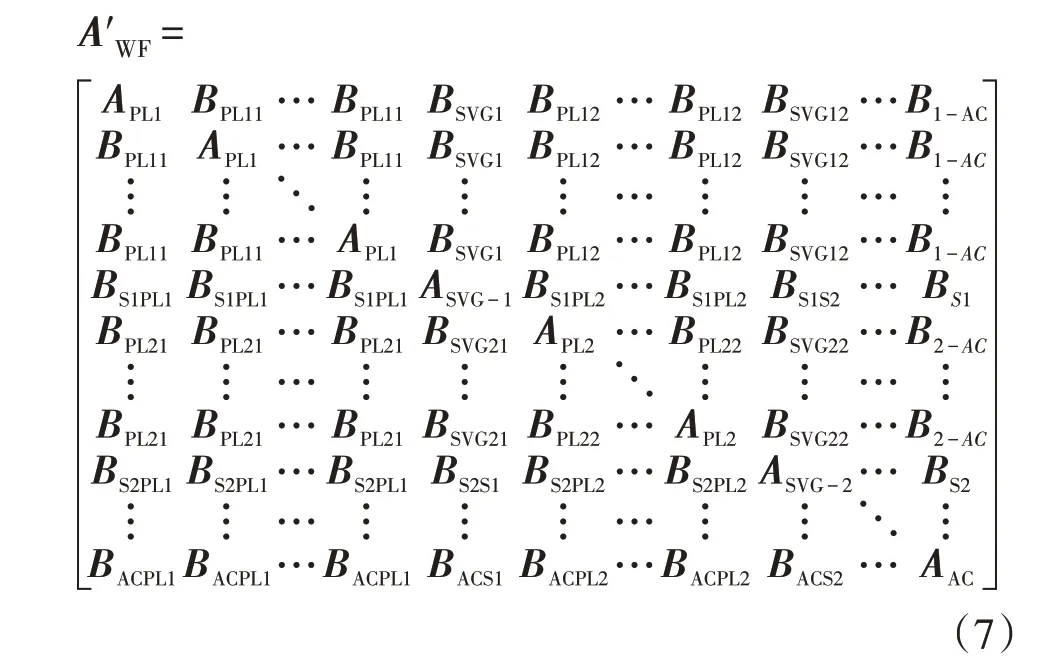
式中:APLi为第i段35 kV 母线下PMSG 的状态矩阵;BPLik为第k段35 kV 母线下PMSG 对第i段35 kV母线下PMSG 的控制矩阵;BSVGik为第k段35 kV 母线下SVG 对第i段35 kV 母线下SVG 的控制矩阵;Bi-AC为交流系统对第i段35 kV 母线下PMSG 的控制矩阵;BSiPLk为第k段35 kV 母线下PMSG 对第i段35 kV 母线下SVG 的控制矩阵;BACPLk为第k段35 kV 母线下PMSG 对交流系统的控制矩阵。
将式(7)带入式(6),并经过行列变换可以得到:
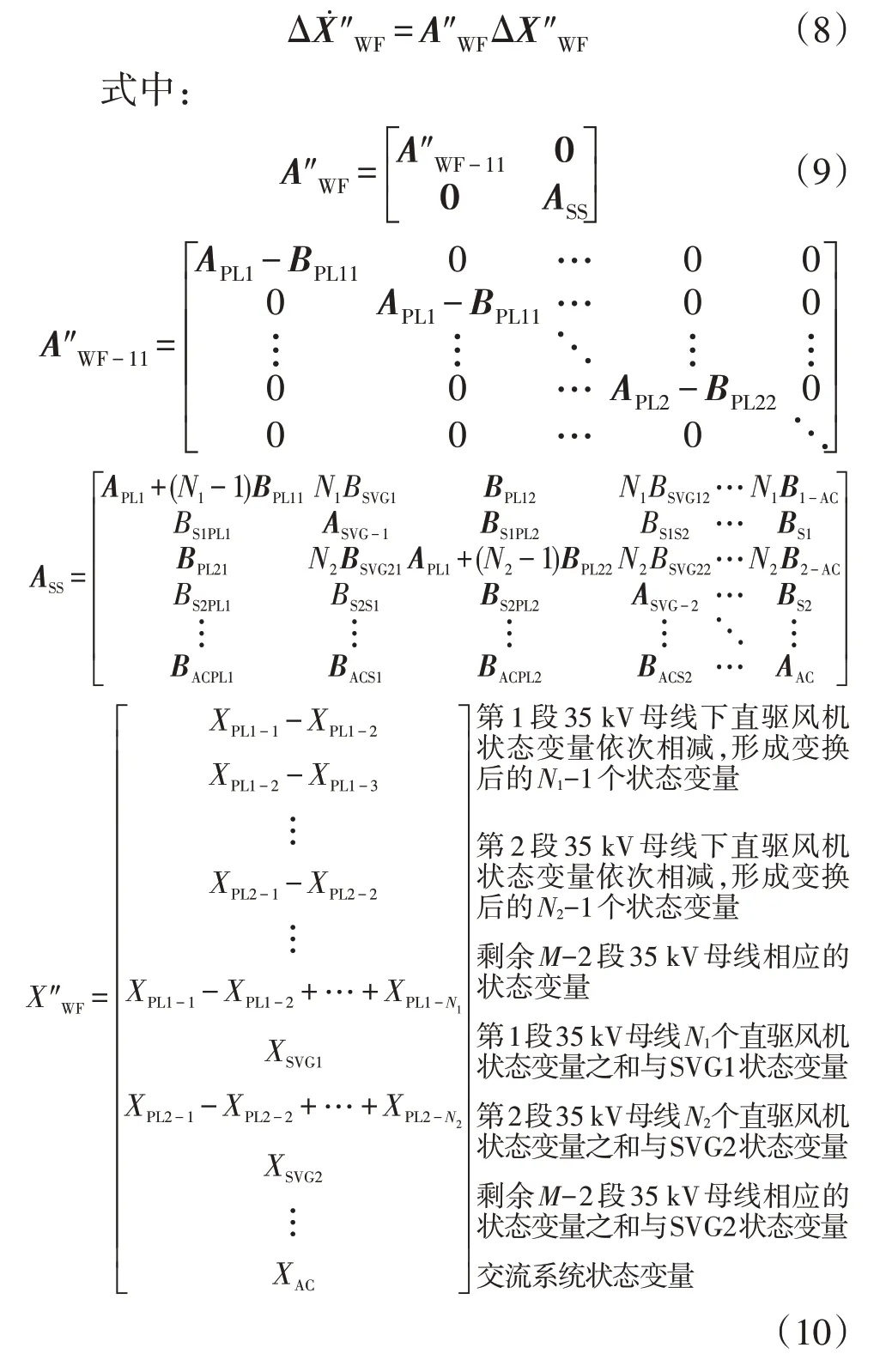
行列变换不会改变状态矩阵的特征值,因此A′WF和A″WF具有相同的特征值。根据式(9),A″WF由N1个APL1-BPL11,N2个APL2-BPL22,...,NM个APLM-BPLMM和剩余子矩阵ASS构成。因此,A′WF的特征值等于子矩阵APL1-BPL11,APL2-BPL22,...,APLM-BPLMM和ASS特征值的集合。通过计算子矩阵APL1-BPL11,APL2-BPL22,...,APLM-BPLMM和ASS来代替计算原始状态矩阵AWF的特征值。因此,采用降阶模型获得系统振荡模式,仅需要计算M个16 阶矩阵和1 个M×(16+9)+K阶矩阵的特征值,远远小于未采用降阶模型时的(N1+N2+…+NM)×16+M×9+K阶矩阵,可以大大减少计算量和时间。
2 含SVG直驱风电场中宽频振荡
本文所采用算例系统如图5 所示,其中含SVG直驱风电场共有2 段35 kV 母线,每段母线下各有5 台PMSG 和1 台SVG,且参数和运行工况均相同;含SVG 直驱风电场附近有1 座火电厂,二者经过交流输电线与无穷大系统相连。初始运行工况为:PMSG 有功功率0.1 p.u.,SVG 无功功率容性0.2 p.u.,风电场母线电压为1 p.u.。其中,PW,QW,Xwt分别为风电场的有功功率、无功功率和升压变压器的电抗;Psg、Qsg、Xgt1分别为同步发电机的有功功率和无功功率和升压变压器的电抗;PL、QL、ZL分别为传输线路上的有功功率、无功功率和线路阻抗;Vs为系统电压。

图5 含SVG直驱风电场并网系统结构图Fig.5 Structure of grid-connected PMSG-based wind farm with SVG
根据第1 节所述方法,建立图5 算例系统的降阶模型,并计算系统的振荡模式,如表1 所示。未采用降阶模型时,系统状态矩阵共有218 阶,占用内存352 kB,耗时0.223 182 s;采用降阶模型,需要分别计算2 个16 阶状态矩阵和1 个65 阶状态矩阵,占用内存38 kB,耗时0.001 395 s;与未降阶模型相比,所占内存减少近90%,计算速度快了100 倍以上。
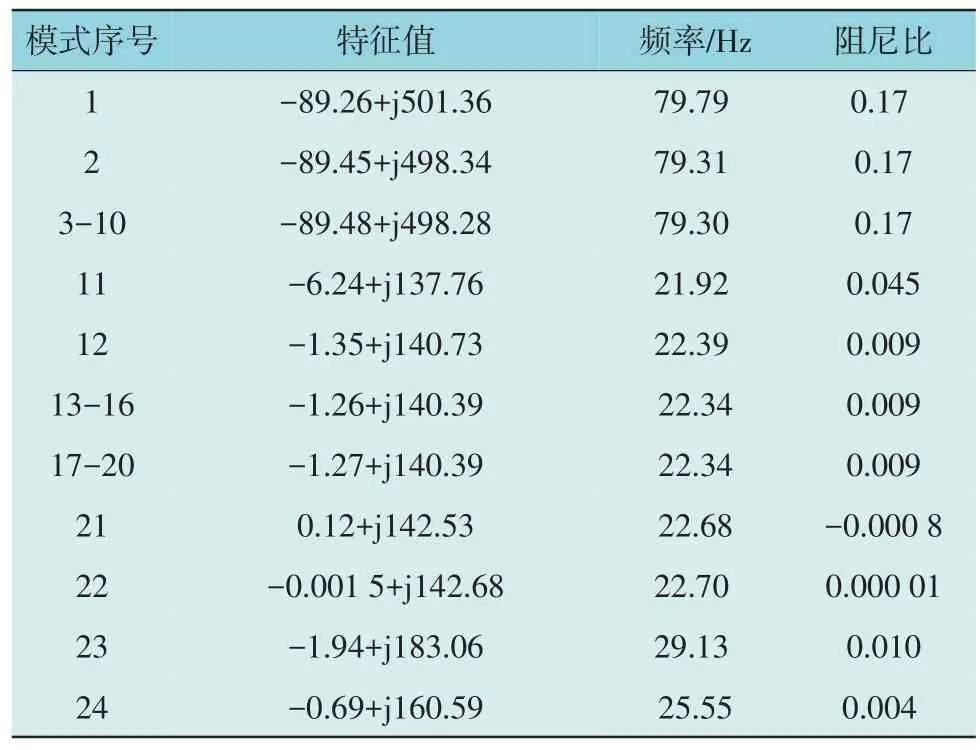
表1 算例系统主要特征值Table 1 Main eigenvalues of example system
由表1 可知,算例系统存在2 个负/弱阻尼振荡模式,模式21:0.12+j142.53,振荡频率为22.68 Hz,阻尼比为-0.000 8,主要与SVG1,SVG2 的q轴电流内环相关;模式22:-0.001 5+j142.68,振荡频率为22.70 Hz,阻尼比为0.000 01,主要与SVG1,SVG2的q轴电流内环相关。模式21 与模式22 的参与因子[20-21]如图6 所示。因此,可以认为含SVG 直驱风电场并网时可能引发宽频振荡问题。
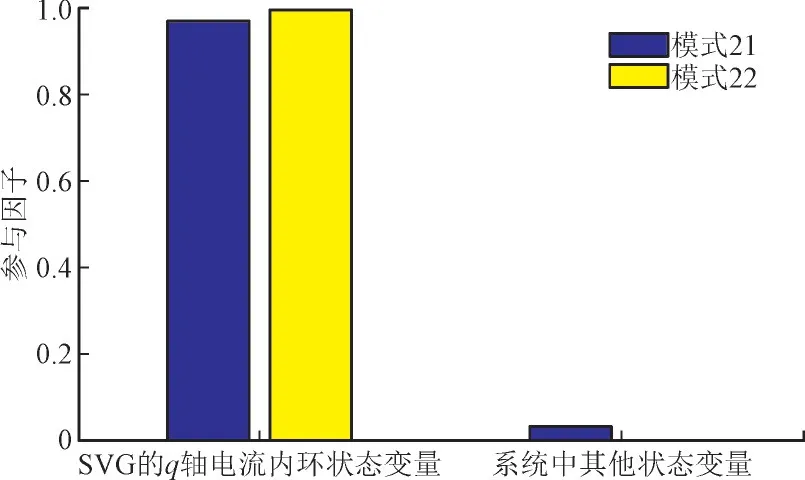
图6 算例系统参与因子Fig.6 Participation factors of example system
3 含SVG 直驱风电场宽频振荡抑制措施
3.1 含SVG直驱风电场宽频振荡阻尼控制器设计方法
在图1 的基础上,在每条35 kV 母线并联SVG的内环控制回路中安装阻尼控制器,以35 kV 母线的电压作为输入信号Uin,其传递函数[22-25]为:
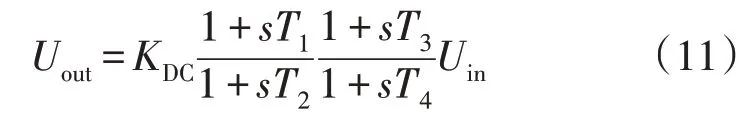
式中:Uin,Uout分别为宽频振荡阻尼控制器输入与输出;KDC为控制器增益;T1—T4为控制器时间常数。
附加宽频振荡阻尼控制器后,SVG 的微分方程变为:
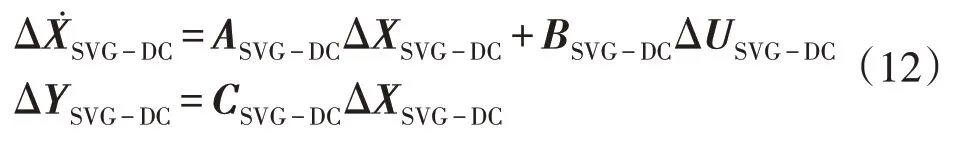
式中:ΔXSVG-DC为附加宽频阻尼控制器后的SVG 的状态变量;ΔUSVG-DC、ΔYSVG-DC、ASVG-DC、BSVG-DC、CSVG-DC分别为附加阻尼控制器后SVG 的控制变量、输出变量、状态矩阵、控制矩阵、输出矩阵。
以含SVG 直驱风电场并网系统目标振荡模式阻尼比为目标函数,以系统中其他振荡模式阻尼比大于0 为约束条件,采用全局优化算法对阻尼控制参数进行优化。令目标函数为:
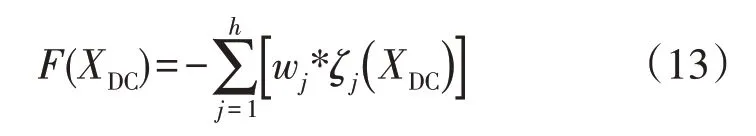
式中:XDC=[T1T2T3T4KDC];ζj为系统中目标振荡模式的阻尼比;wj为的权重系数(j=1,2,…,h)。
令不等式约束为:

式中:ζother为其他振荡模式的阻尼比。
3.2 抑制措施效果验证
针对图5 中算例系统,采用3.1 中提出的方法设计含SVG 直驱风电场宽频振荡阻尼控制器,得到附加宽频振荡阻尼控制器后系统的主要振荡模式,如表2 所示。
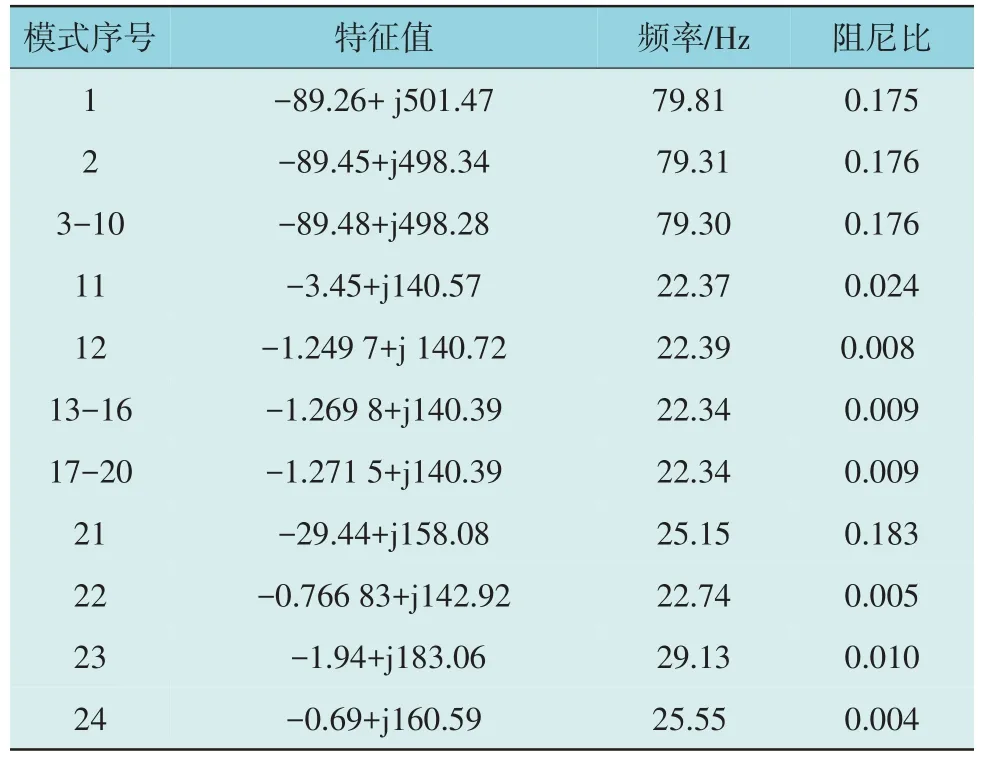
表2 附加宽频振荡阻尼控制器后的算例系统主要特征值Table 2 Main eigenvalues of example system with wideband oscillation damping controller
由表2 可知,附加宽频振荡阻尼控制器后,系统中振荡模式均为正阻尼,系统是稳定的。
图7 为附加宽频振荡阻尼控制器前后,含SVG直驱风电场并网系统的时域仿真曲线。

图7 附加宽频振荡阻尼控制器前后系统时域仿真Fig.7 Time domain simulation of system with and without wideband oscillation damping controller
如图7 所示,未附加宽频振荡阻尼控制器时,故障后直驱风机、SVG 功率中均存在23 Hz 左右的振荡;附加宽频振荡阻尼控制器后,故障后直驱风机、SVG 功率快速趋于稳定,振荡得到有效地抑制。因此,说明3.1 中提出的含SVG 直驱风电场宽频振荡阻尼控制器设计方法是有效的。
4 结论
本文建立了含SVG 直驱风电场并网系统的降阶状态空间模型,发现风电场内SVG 可能引发宽频振荡,在降阶模型的基础上分析了风机台数、风机有功功率、SVG 无功功率、风电场母线电压等因素对目标振荡模式的影响;为了抑制振荡,提出了含SVG 直驱风电场宽频振荡阻尼控制器设计方法。结论如下:
1)基于含SVG 直驱风电场并网系统降阶状态空间模型,不会因风机台数增加而大幅增加额外的计算量;根据降阶状态空间求解目标振荡模式极大地减少了计算资源与计算时间。
2)含SVG 直驱风电场并网时,系统中可能存在与SVG 相关的负阻尼宽频振荡模式。
3)模态分析结果和时域仿真结果均验证了含SVG 直驱风电场宽频振荡阻尼控制器设计方法可以有效抑制含SVG 直驱风电场中的振荡现象。

