基于LM法的换流站关键设备宽频建模方法研究
董靓靓,王顺亮,马俊鹏,刘天琪,彭光强,吴子豪,王若谷
(1.四川大学电气工程学院,四川 成都 610041;2.南方电网超高压输电公司检修试验中心,广东 广州 510700;3.国网陕西电力科学研究院,陕西 西安 710100)
0 引言
近年来,直流输电工程在解决我国西南地区水电消纳问题过程中起着举足轻重的作用[1-3]。直流输电系统换流站具有交直流谐波变换作用[4-6],呈现出宽频谐波特性,而直流系统换流站中的某些元件在不同频率下所表现出的阻抗特性有所差异,为了给直流输电系统相关研究提供更为准确的电磁暂态仿真模型,有必要提出准确的宽频建模方法,建立宽频等效电路。
对于建立高压直流换流站电磁骚扰的高频段(1 MHz—100 MHz)宽频模型已经有了较多研究[7-10],给1 MHz 以下频段建模提供了参考。文献[11]建立了LCC 换流阀、换流变等直流换流站一次回路宽频等效电路,但是并未表明建模方法;文献[12]采用传统方法针对换流系统电磁骚扰特性进行宽频建模研究,测取设备频率-阻抗特性后通过矢量匹配法(Vector Fitting,VF)提取零极点,进行网络综合得到了阀组件等的高频段黑箱模型。然而,这种建模过程较为复杂。文献[13]从元件物理结构出发,将高压换流阀内各元件的宽频模型串、并联后获得集成模型,通过谐振频率预估元件参数,通过阻抗曲线拟合优化参数,但当建模频段不存在谐振点时可能导致该方法失效;文献[14]通过遗传算法计算高频段等效模型元件参数,保证了计算结果的准确性。文献[15]通过阻抗分析仪测量不同端口条件下的阻抗特性提取了多绕组中频变压器的寄生参数并进行仿真验证,但并未提及如何通过端口阻抗特性获得寄生参数,且高频段阻抗特性误差较大。文献[16]研究了绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor,IGBT)阀杂散参数的分布,分析了杂散参数对IGBT 串联阀开通过程的影响;文献[17]根据电感的尺寸、结构和材料计算出电抗器绕组间、层间和匝间寄生电容参数,建立了中压滤波电感的物理模型。随着我国直流输电工程不断建设,对直流输电换流站关键设备进行宽频建模具有重要意义,现有研究的宽频建模方法精度不能满足要求,建模过程较为复杂。
本文通过建立直流换流站关键电气设备物理模型,基于LM[18]法提取模型参数,搭建了其宽频模型并进行简化。然后,通过设备阻抗特性实际测量与宽频模型仿真结果对比,验证了宽频等效模型及所提方法的正确性,并通过与传统建模方法对比,凸显了本文所提方法的优势。最后,将所建模型应用于混合直流输电系统,对比分析了宽频模型和理想模型谐波特性的异同。
1 宽频建模与参数提取方法
1.1 宽频建模方法
对于任意的RLC 等值网络,其复频域阻抗Z(s)可以表示为:

式中:a0,a1,a2…an,b0,b1,b2…bn为含有元件参数的未知系数。
通常期望表达式的拟合后的误差为0,则有:

将式(2)两边同时乘上D(s)后得到:

其中,e′(s)仍然为0,展开后可得:

由式(4)可以构造为:

一般b0已知为0 或1,矩阵A由k个频率阻抗测量值表示为:

向量B由阻抗测量值表示为:

未知系数的解向量x为:
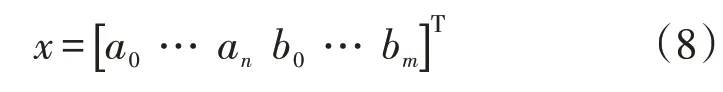
若b0未知,只需将b0加入解向量,并将向量B设为零向量即可求解。在实际工程中,为了得到准确的元件参数,通常测取的频率点个数都远大于未知量的个数,因此,式(5)为超定方程。
1.2 列文伯格-马夸尔特算法方法
列文伯格-马夸尔特算法(Levenberg Marquardt,LM)法是一种改进的牛顿法,也是一种非线性最小二乘算法,该方法通过迭代计算残差平方和来评价是否达到最优拟合,是求解式(5)的一种有效方法,目标函数可表示为:

式中:aij为矩阵A的元素;bi为向量B的元素;xj为解向量x的元素;M为解向量元素的个数;N为测量点的个数;a为迭代系数;v i为加权系数。
通过循环迭代令当前拟合系数acur趋近于最小值amin,即可获得最优解,即:
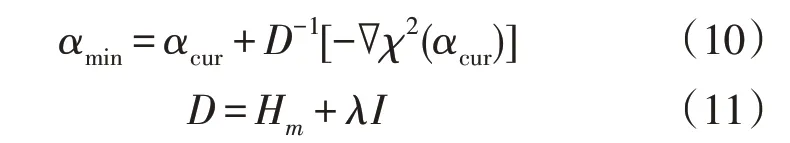
式中:Hm为海森矩阵;I为单位矩阵;l为阻尼系数,通常海森矩阵的影响可被忽略。
1.3 技术优势
传统宽频建模方法[12,19-20]将待测元件视作黑箱,测取阻抗特性后进行网络综合推测出元件宽频等效电路,然而基于黑箱建立的等效电路可能不符合元件实际物理结构导致所建模型物理意义不明确。
同时,由于传统方法采用的VF 法将式(1)化为式(12),即:

进行拟合时需要假设一系列初始极点an,而初始参数设置较困难,会极大的影响拟合结果,需要复杂的初始极点筛选程序,增加了算法复杂度。
当电路阶数较低时,VF 法失效,拟合误差很大,无法进行网络综合得到准确的宽频等效模型。因此,为解决以上问题本文提出了适用于物理模型已知的情况下的宽频建模方法。
2 换流站关键设备宽频建模
2.1 截止状态晶闸管宽频模型
换流阀由多级晶闸管串联构成[21],其中每个晶闸管由3 个PN 结构成[22],是一种典型的四层三端非线性元件。在正常工况下,换流阀晶闸管主要有导通和截止两种工作状态。由半导体器件的性质可知,导通状态的晶闸管电阻几乎为零,因此可以忽略不计。本文将导通状态的晶闸管视为短路,不考虑其阻抗特性,仅测量截止状态下的阻抗特性并将其视为线性元件,对其进行宽频建模研究。
因此,考虑杂散参数的晶闸管宽频等效电路如图1 所示,Cj为PN 结耗尽层电容,R为晶闸管关断电阻,Ll和Rl为晶闸管的杂散电感和杂散电阻。

图1 截止状态晶闸管宽频等效模型Fig.1 Broadband equivalent model of cut-off state thyristor
图1 所示的晶闸管宽频等效模型阻抗Z(s)可以表示为:

根据式(4)和式(5)可将式(15)表示为:

将实测数据代入式(14),采用LM 算法求得解向量x,然后求解非线性方程组得到宽频等效模型参数R,Cj,Ll和Rl。
2.2 平波电抗器宽频模型
图2 为平波电抗器的宽频等效模型[23-24],其中Ll,Rl为电抗器的电感和电阻,Ck为电抗器两端的漏电容,Cg为电抗器两端对地的漏电容。

图2 平波电抗器宽频等效模型Fig.2 Broadband equivalent model of flat-wave reactor
2.3 换流变压器
换流变压器宽频等效模型[25-26]如图3 所示。换流变寄生电容主要为网侧对地电容C1,阀侧对地电容C2,网侧相间寄生电容CAB,CBC,CAC,阀侧相间寄生电容Cab,Cbc,Cac,网侧绕组寄生电容CkA,CkB,CkC,阀侧绕组寄生电容Cka,Ckb,Ckc,网侧与阀侧绕组间寄生电容C12。漏感和铜耗电阻主要为网侧漏感LkA,LkB,LkC,阀侧漏感Lka,Lkb,Lkc,网侧铜耗RkA,RkB,RkC,阀侧铜耗Rka,Rkb,Rkc。在低频段,主要体现出绕组漏感和铜耗等宽频特性参数的影响,高频段则需要考虑其寄生电容参数的影响。

图3 换流变压器宽频等效模型Fig.3 Broadband equivalent model of converter transformer
2.4 滤波器
直流输电系统换流站滤波器主要有装配在LCC 换流站的直流滤波器[26]和交流滤波器[27],典型等效电路如图4 和图5 所示。

图4 交流滤波器宽频等效模型Fig.4 Broadband equivalent model of AC filter

图5 直流滤波器宽频等效模型Fig.5 Broadband equivalent model of DC filter
由于滤波器的漏感、铜耗和寄生电容参数远小于自身元件参数值,故在宽频建模过程中均可忽略。
3 宽频建模方法验证与应用
3.1 宽频模型参数提取及验证
本文首先根据换流站关键电气设备的物理模型建立宽频等效电路,将电路中未知的元件参数设为未知量,建立元件含有未知量的阻抗-频率表达式。在测取设备的阻抗-频率函数后,利用LM 法获取宽频模型参数。
3.1.1 晶闸管宽频模型参数提取及验证
在实验室中,通过数字电桥测量晶闸管的频率-阻抗特性,如图6 所示。由于晶闸管的单向导通特性,在测试时,外加30 V 反向直流偏置电压,选取10 Hz—300 kHz 的频带范围对晶闸管进行扫频测试,获得测量值100 个。

图6 晶闸管阻抗测量Fig.6 Impedance measurement of thyristor
晶闸管频率-阻抗特性测量结果与宽频模型拟合曲线如图7 所示。

图7 晶闸管测量结果和拟合曲线Fig.7 Measurement results and fitting curves of thyristor
通过LM 方法求解得到晶闸管宽频模型各元件参数如表1 所示。晶闸管相频特性在测量频段内呈现为纯容性,且提取的图1 中的杂散电感Ll值较小,因此,用于电磁暂态仿真时,可忽略杂散电感Ll的影响。同时,杂散电阻Rl≪R,其影响也可忽略不计,以此简化晶闸管宽频模型。

表1 晶闸管宽频模型各元件参数值Table 1 Parameter value for each component in broadband model of thyristor
3.1.2 平波电抗器宽频模型参数提取及验证
在测量时,平波电抗器无需外加直流偏置电压选取10 Hz—300 kHz 的频带范围对晶闸管进行扫频测试,获得测量值100 个。
采用LM 法获得的宽频模型各元件参数如表2所示。平波电抗器频率-阻抗特性测量结果与宽频模型拟合曲线如图8 所示拟合结果显示出计算结果与测取的数据之间误差较小。忽略Rl的影响对阻抗特性的影响极小,因此在宽频模型的等效电路中可以直接将平波电抗器的电阻Rl删除。

表2 平波电抗器宽频模型各元件参数值Table 2 Parameter value for each component in broadband model of flat-wave reactor

图8 平波电抗器测量结果和拟合曲线Fig.8 Measurement results and fitting curves of flatwave reactor
3.2 宽频建模结果对比
电路阶数较低时,传统建模方法[10,27]拟合误差很大,图9 对比了传统方法和本文建模法对晶闸管阻抗特性的拟合结果。本文提出的先建立物理模型,再通过LM 法提取元件参数的方法具有较高准确度,适用于高阶和低阶电路。

图9 不同方法下晶闸管阻抗特性拟合结果对比Fig.9 Comparison of fitting results of thyristor impedance characteristics between different methods
3.3 宽频模型与理想模型谐波特性对比
由于对直流输电系统谐波特性的研究一般关注100 kHz 以下频段,而在该频段不会体现出复杂的宽频特性。因此,将上节提取的宽频等效电路中使用简化等效电路。本节将宽频模型应用到直流输电系统PSCAD 模型中,并与理想模型仿真结果对比。在仿真模型中,LCC 换流站采用双极直流输电方式,每一极由两个十二脉动换流器串联而成,其中,十二脉动换流器的理想模型由两个六脉动换流器串联组成。
图10 和图11 为LCC 换流站理想模型和宽频模型换流变压器阀侧电压波形和谐波含量对比,显示了谐波变化情况,对比结果显示,将理想器件替换为宽频模型后,换流变阀侧电压谐波特性发生变化,其中,5 次谐波幅值变化最大,约为基波的1.7%。

图10 LCC换流变阀侧电压波形对比Fig.10 Comparison of waveform for LCC converter transformer valve side voltage

图11 LCC换流变阀侧电压谐波含量对比Fig.11 Comparison of harmonic content for LCC converter transformer valve side voltage
两种模型的换流变压器阀侧电流波形和谐波含量对比如图12 和图13 所示,结果表明LCC 换流站换流变阀侧电流5 次谐波减小约1.8%。在0—2 000 Hz 频段各元件宽频模型不存在谐振点,此时由于宽频模型中的无源LC 元件能够抑制冲击,让波形更加平滑,从而使得波形更加接近正弦波,谐波减小。

图12 LCC换流变阀侧电流波形对比Fig.12 Comparison of waveform for LCC converter transformer valve side current
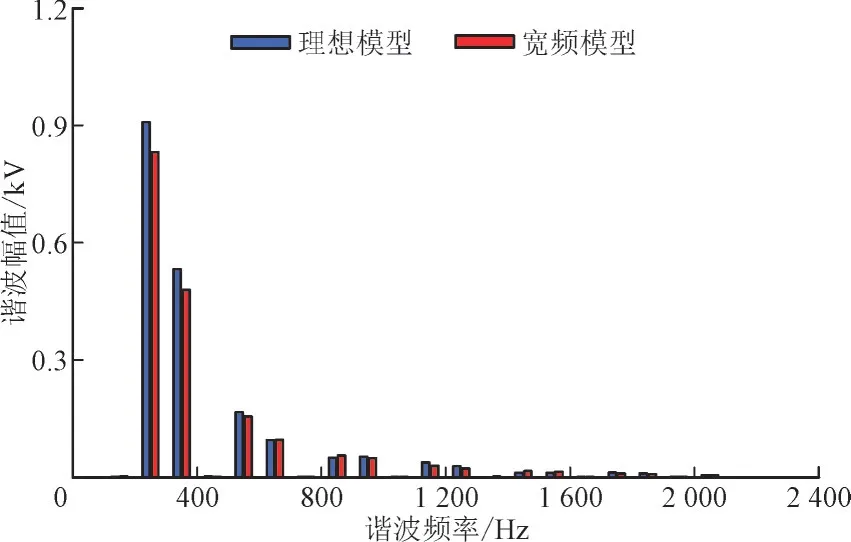
图13 LCC换流变阀侧电流谐波含量对比Fig.13 Comparison of harmonic content for LCC converter transformer valve side current
3.4 仿真速度对比
本文对未简化的宽频模型和简化后的宽频模型三种不同模型的仿真速度进行了对比,采用控制变量法,仿真时间分别设定为1、3、5 s,仿真步长均设定为100 ms,3 种模型完成仿真的用时如表3 所示,可见加入未简化的宽频参数后仿真时间会增长约30%,而简化后的宽频模型可以节省仿真时间约12%,因此,简化模型十分必要。

表3 各模型仿真速度Table 3 Simulation speed of each model
4 结论
本文研究了直流输电系统换流站关键设备宽频阻抗模型建立与简化方法,通过实际元件阻抗测量与计算结果对比验证了算法的有效性,并对比了换流系统理想模型与宽频模型的谐波特性,得到如下结论:
1)本文所提建模方法拟合精度高,可有效用于换流站关键设备的宽频建模。
2)换流站关键设备中部分较小的高频杂散参数对换流站低频段(<2 kHz)的影响较小,可以将其忽略以简化模型,简化模型后可以节省仿真时间。
3)本文建立了换流站关键设备宽频等效模型提出了模型参数获取与模型简化方法,降低了仿真模型的复杂度,并兼顾换流站关键设备的寄生参数。

