基于领域自适应的变压器状态识别
甘团杰,郑建涵,张 艳,张 昶,黄 敏,李 中
(1.广东电网有限责任公司江门供电局,广东 江门 529000;2.华南理工大学软件学院,广东 广州 510006;3.华北电力大学电子与通信工程系,河北 保定 071003)
0 引言
变压器是电网中连接各个区域输配电的枢纽,变压器一旦发生故障,严重影响电力系统的正常运行,造成负荷大面积失电等严重事故,并带来一定的经济损失[1]。识别和监测变压器的状态,提早发现变压器状态的恶化趋势,避免其发展到故障程度,规避事故的发生,有利于降低电力系统的脆弱性[2],因此开展变压器的状态识别研究具有重要的理论意义和工程应用价值。
传统的变压器状态识别方法主要包括贝叶斯网络[3]、支持向量机[4]、模糊评判[5]和特征气体浓度比值法[6]等,传统方法原理简单,对数据量的要求比较小,但存在特征提取和利用能力不足的问题,导致状态识别精度有限。随着机器学习技术的发展,出现了基于随机森林[7]、卷积神经网络[8]、深度信念网络[9]和自动编码器[10]等方法,在满足训练和测试数据同来源和同分布情况下,能够很好地学习特征取得很高的状态识别精度。然而,在实际应用中,模型训练和测试所用数据的来源和分布往往是不一致的,这导致了这些方法存在着泛化能力不足的问题。
迁移学习(Transfer Learning,TL)是近年来发展迅速的一种方法,它能够把在一个领域(源域)内学习到的知识进行提取,并迁移到新的领域中,以帮助新领域(目标域)中的学习任务,可以有效地解决算法模型泛化能力不足的问题[11]。领域自适应(Domain Adaptation,DA)是迁移学习的重要分支,已在机械轴承[12-13]、齿轮箱[14-15]、风力涡轮机[16]等设备的状态识别中应用较多,在电力设备状态识别中应用前景良好[17]。本文利用一种基于流形嵌入和动态分布对齐的领域自适应方法训练了一个泛化能力强的变压器状态识别分类模型。首先,建立了多尺度的时频分析方法,利用变分模态分解对变压器振动信号进行分解,并且分别提取原始信号和模态分量的时域、频域、熵特征,构建完备的变压器状态描述特征空间;然后,将特征空间嵌入格拉斯曼流形空间中进行流形特征变换,并对变换后的源域及目标域的流形特征进行动态分布对齐,量化考虑了流形特征边缘分布和条件分布对变压器状态识别的重要性;最后,基于结构风险最小化原则迭代训练得到变压器状态识别分类器。
1 领域自适应和多尺度特征提取
1.1 迁移学习和领域自适应
迁移学习是一种机器学习方法,能够提取源域内学习到的知识,并将其迁移到不同但相关的目标域中,以帮助学习目标任务。领域是迁移学习的主体,主要由数据和数据的概率分布构成,记为D={X,Y,P(x,y)},其中,x和y分别为数据特征和标签,X和Y分别为数据所处的特征空间和标签空间,P(x,y)为数据服从的分布。源域Ds是训练样本所在的、有丰富标注和知识的领域,目标域Dt是目标测试样本所在的、待学习的领域。本文记号约定,具有下标s 的量为源域相关,具有下标t 的量为目标域相关。知识从源域传递到目标域的过程即为迁移。当源域和目标域的特征空间及标签空间均相同,仅有数据分布不同(领域偏移)时,迁移学习被称为领域自适应。领域自适应的目标是利用源域数据去学习目标域上的1 个预测函数f:xt↦yt,使得f在目标域上拥有最小的预测误差O′,即:
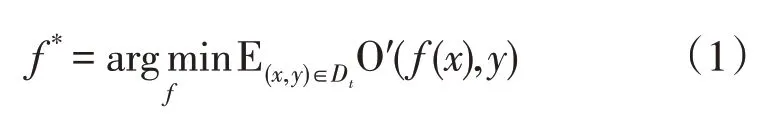
迁移学习的核心是找到并充分利用源域和目标域之间的相似性,如何度量这种相似性是首先需要解决的问题。在领域自适应中,相似性被刻画为领域之间的分布差异,则领域自适应的目标可以被描述为寻求某种方法,使得领域之间的分布差异最小。
1.2 基于流形嵌入和动态分布对齐的领域自适应
领域偏移会导致源域模型直接应用于目标域时精度不高,出现泛化能力弱的问题。基于流形嵌入和动态分布对齐的领域自适应方法因其具有一系列优良性质[18],能够减弱领域偏移的影响,提高模型精度和泛化能力。
基于流形嵌入的领域自适应旨在将源域和目标域映射到同一个流形空间中,借助流形空间良好的几何结构,将源域和目标域变换到同一子空间中,能够简化领域之间的分布差异的计算。
本文采用测地线流式核(Geodesic Flow Kernel,GFK)方法[19]。首先,利用主成分分析将源域和目标域的特征空间映射到格拉斯曼流形空间G中,分别记为Ss和St,每个嵌入G中的特征子空间被看做是G中的1 个点。GFK 在G中寻找1 条测地线Φ(·),使得源域Ss=Φ(0)可以通过这条测地线经由g(·)变换到目标域St=Φ(1)。其计算如式(2)所示:

GFK 提取出流形可迁移特征后,对源域和目标域特征进行分布自适应,即减小分布之间的差异。然而,边缘分布和条件分布并不是同等重要的,当源域和目标域数据本身存在较大差异时,边缘分布自适应更重要,当两域数据有较高相似性时,条件分布自适应更重要。因此,引入动态平衡因子μ对边缘分布和条件分布进行量化[18],μ能够根据实际数据分布的情况,动态地调整每个分布的重要性,动态分布对齐函数如式(3)所示。
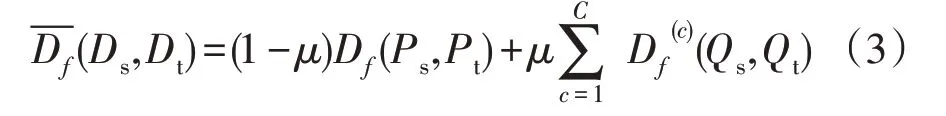
式中:c∈{1,2,...,C},为分类标签;P和Q分别为数据的边缘分布和条件分布;Df(Ps,Pt)和Df(c)(Qs,Qt)为对应的分布自适应函数。
结合最大均值差异(Maximum Mean Difference),在再生核希尔伯特空间(记为Hk)中,式(3)转化为式(4),即:
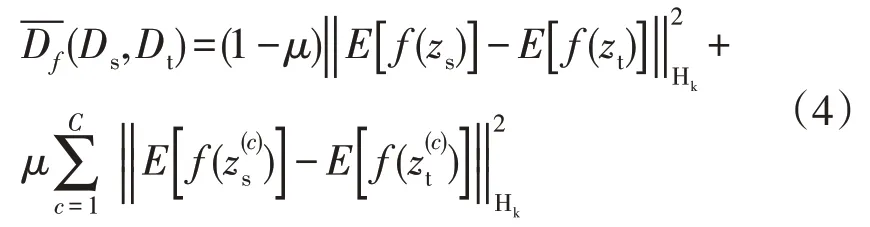
但是直接计算Df(c)(Qs,Qt)存在困难,利用ADistance[20]对其进行估算,计算得到的源域目标域之间的边缘分布差异记作AM,条件分布差异记作AC,则动态平衡因子μ可以用式(5)估算得到:
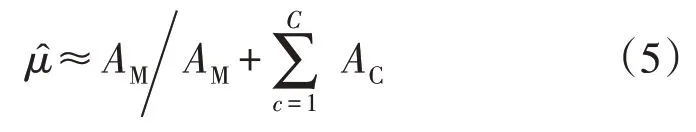
最后,基于结构风险最小化原则设计的领域自适应损失函数L如式(6)所示,其中,首项为交叉熵损失函数l,即经验风险;第2 项为避免源域训练过拟合的正则化项;第3,4 项为分布差异度量及相应的正则化项;Rf为拉普拉斯正则化项;η,λ,ρ为权衡因子。即:
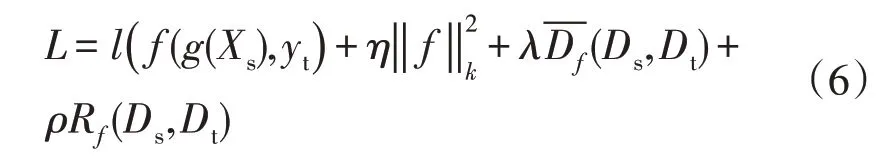
1.3 变分模态分解
变压器的振动复杂[21]通常由多种模态叠加而成,包含着大量信息。为了挖掘其中蕴含的变压器状态信息,需要对振动信号进行分解,抽取出有用的模态信息,削弱噪声模态信息和无关模态信息的干扰。
作为一种自适应、准正交、完全非递归的模态分解方法,变分模态分解(Variational Mode Decomposition,VMD)[22]旨在将信号分解为指定个数的本征模函数(Intrinsic Mode Function,IMF),并且能够在求解变分问题最优解的过程中自适应地匹配每个IMF 的最佳中心频率和有限带宽。同经典的经验模态分解[23]相比,VMD 克服了端点效应和模态混叠问题,能够分解得到包含多个不同频率尺度且相对平稳的IMF。VMD 的算法核心在于构建和求解变分问题。式(7)—式(12)为VMD 计算过程。
假设原始信号f(t)被分解为K个IMF,为了保证第k个(k=1,2,…,K)IMF 分量uk具有中心频率ωk和有限带宽,以及IMF 估计带宽之和最小,并且约束所有IMF 之和等于原始信号,则可以构造出如式(7)所示的变分问题,其中δ(t)为狄拉克函数,*为卷积运算符。即:
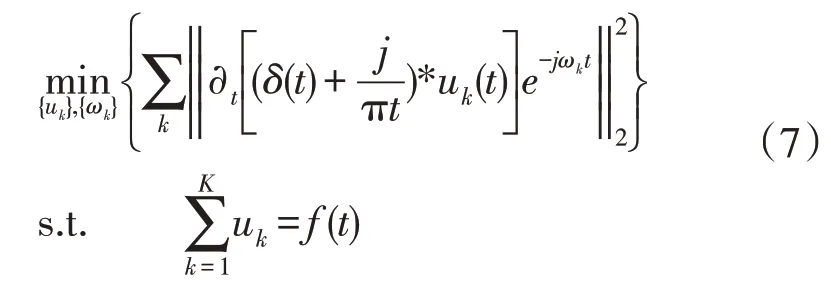
为了高效地求解式(7),并且降低高斯噪声的干扰,引入拉格朗日乘子λ和二次惩罚因子α,将约束变分问题转化为非约束变分问题,得到式(8):
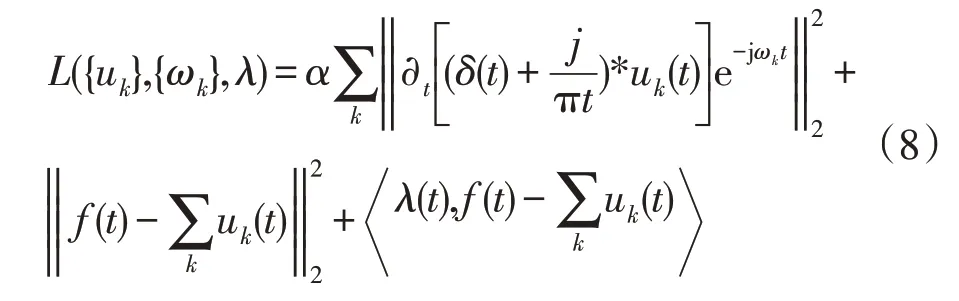
利用交替方向乘子迭代算法结合傅里叶等距变换,优化得到IMF,交替寻优迭代后更新的uk,ωk,λ的表达式如式(9)—式(11)所示,迭代的终止条件如式(12)所示。其中为对应·的傅里叶变换;τ为噪声容忍度;ε为收敛容差。即:
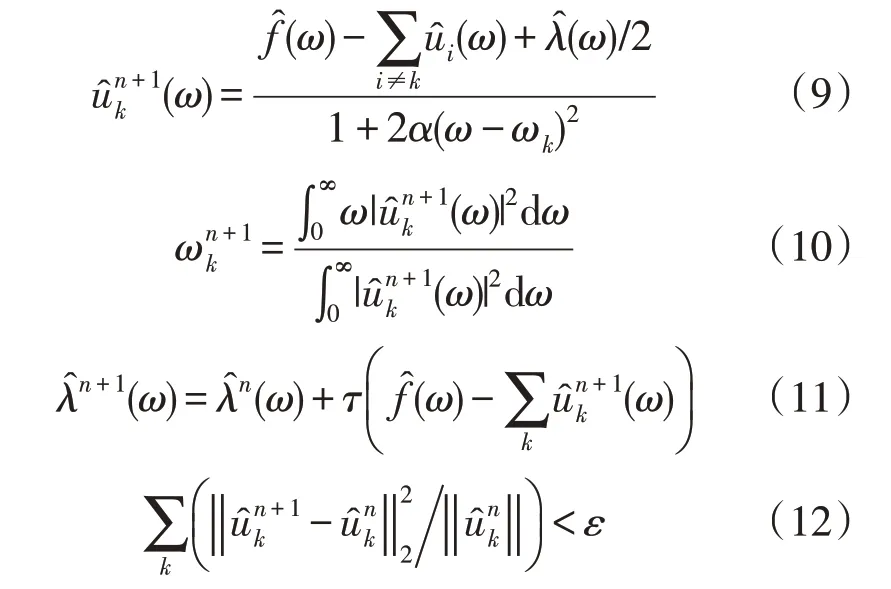
1.4 多尺度特征提取
变压器状态发生变化时,变压器的振动特征随之发生变化,主要包括时域的振动幅值和概率分布,频域的不同频率能量分布,以及熵值反映的结构分布和复杂度等。为了挖掘变压器振动信号的状态信息和固有属性,构建完备的变压器状态描述特征空间,对变压器振动的原始信号和经过VMD分解后的模态分量进行了多尺度的特征提取。
使用统计方法提取了15 种时域特征,表达式如表1 所示,其中xi为振动信号时序序列,i=1,2,...,N,x为振动信号时序序列,N为数据样本点数。特征F1-F8为有量纲的参数,分别为绝对峰值、峰峰值、均值、绝对均值、方根幅值、方差、标准差、均方根值;特征F9-F14为无量纲的参数,分别为峰度、偏度、波形因子、峰值因子、脉冲因子、裕度因子。

表1 时域特征参数表达式Table 1 Expression of time-domain feature parameters
使用统计方法提取了10 种频域特征,表达式如表2 所示,其中,s为信号x的频谱;j=1,2,...,J,J为谱线数;fj为第j条谱线的频率值。特征F15反映频域振动能量的大小,特征F16-F19,F23-F24反映频谱的集中程度,F20-F22反映主频带位置的变化。此外,还提取了能够反映变压器状态动态变化的近似熵[24]、样本熵[25]、模糊熵[26]、排列熵[27]。

表2 频域特征参数表达式Table 2 Expression of frequency-domain feature parameters
2 模型构建
针对现有的变压器状态识别模型泛化能力低的问题,提出了一个基于领域自适应的模型,流程如图1 所示。
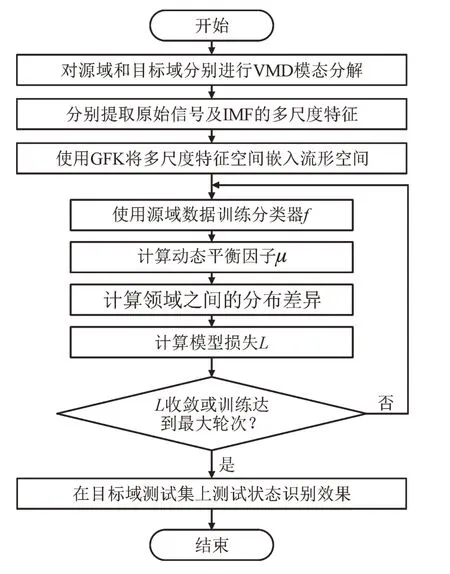
图1 基于领域自适应的变压器状态识别模型Fig.1 Transformer condition identification model based on domain adaptation
基于领域自适应的变压器识别模型主要步骤为:(1)数据采集与预处理阶段。使用加速度计采集不同来源(包括变压器型号、工况、采集部位的不同等)的变压器振动数据;(2)多尺度特征提取阶段。首先将原始振动信号进行变分模态分解,然后将模态分量和原始信号分别进行3 个域的特征提取,并且对各特征进行z分数标准化,构建一个完备的状态特征空间;(3)领域自适应阶段。首先将特征空间映射到格拉斯曼流形空间中,然后通过动态分布对齐,对边缘分布和条件分布的重要性进行量化评估,基于梯度回传最小化式(6)迭代训练分类器,最终输出变压器状态识别分类器f。其中,变分模态分解(VMD)以及基于流形嵌入和动态分布对齐(MEDA)的参数设置如表3 所示。
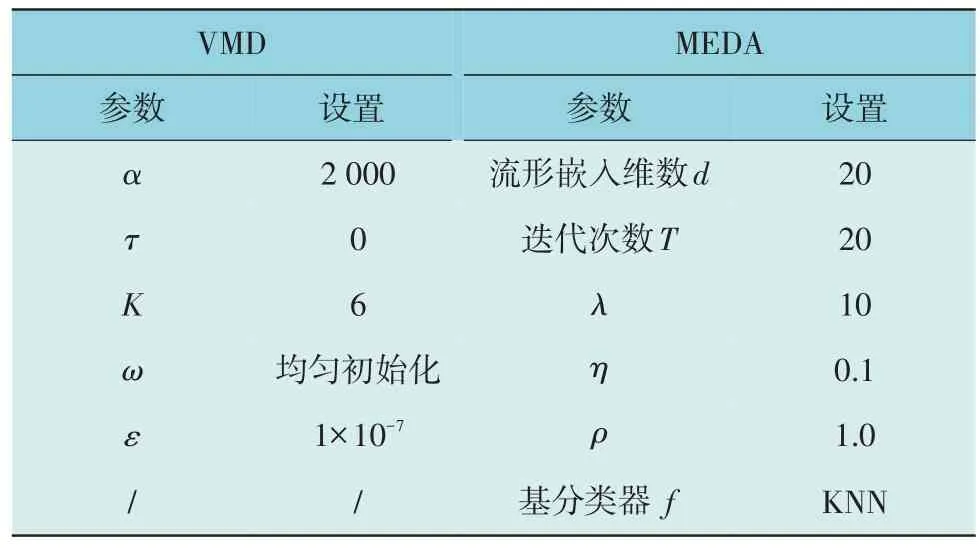
表3 模型参数设置Table 3 Setting of model parameters
3 实验验证与结果分析
3.1 数据介绍
使用振动传感器采集了某变压器的振动信号和工况数据,每5 min 进行1 次采样,每次采样时长为1 s,采样频率为10 kHz,共采集到238 组样本。所测变压器参数如表4 所示。
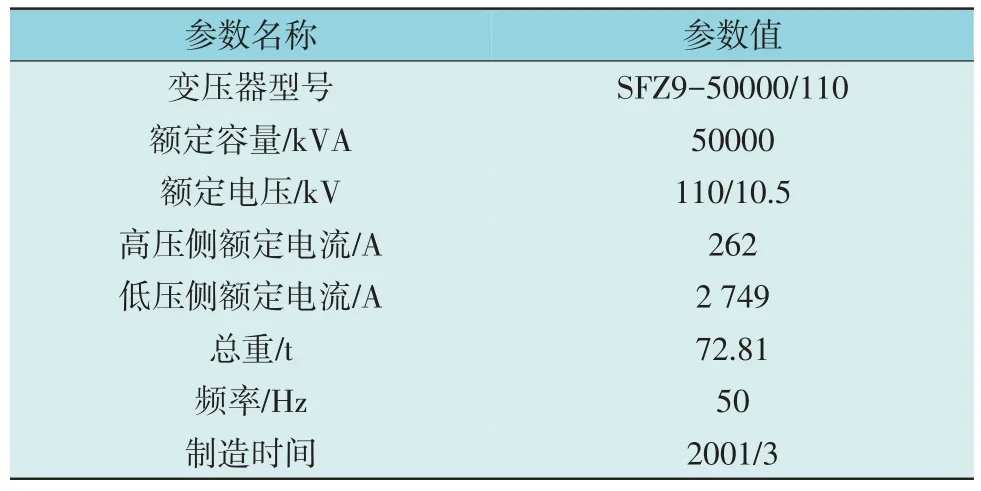
表4 所测变压器的参数Table 4 Parameters of experimental transformer
在高低压三相接线柱正下方均安装了振动传感器,安装位置为距离油箱底部1/3 高度处,分别记为测点A,a,B,b,C,c,如图2 所示。
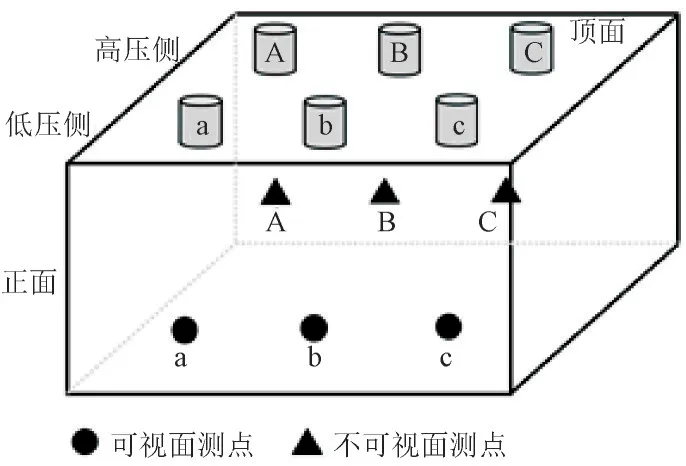
图2 振动传感器测点安装位置示意图Fig.2 Installation position of vibration sensor at measuring point
不同测点的数据分布如图3 所示,采集自不同部位的振动数据的分布特征有巨大差异,这会导致以单一来源数据训练的变压器状态识别模型泛化能力不足。
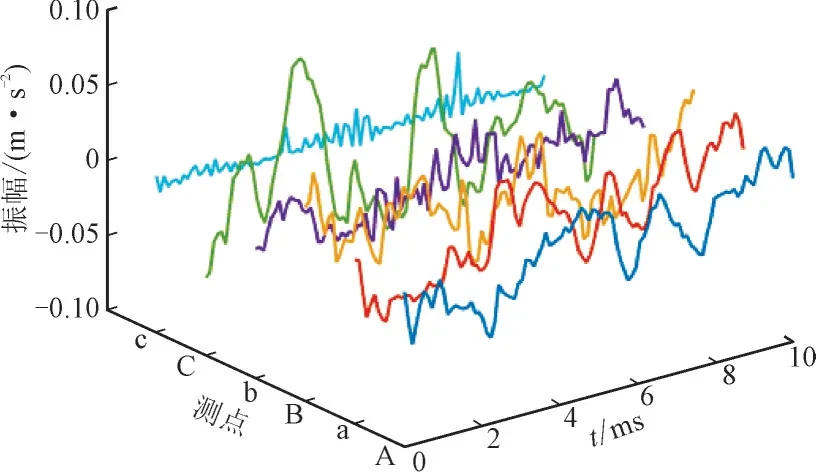
图3 不同测点的数据分布Fig.3 Data distribution of different measuring points
3.2 实验结果与分析
按照额定电压的1,+1.5%,+3%和高压侧额定电流的0,+20%,+40%,+60%对数据进行工况划分,得到6 类工况数据,如图4 所示。

图4 变压器工况划分Fig.4 Division of transformer conditions
原始数据(黑色线)和经过VMD 得到的6 个模态分量(彩色线)的振动波形图如图5 所示,经快速傅里叶变换得到的频谱图如图6 所示。VMD 有效地将多模态叠加的振动信号分解成了频率成分较为单一的多个分量,利于减少无关模态和噪声的干扰。
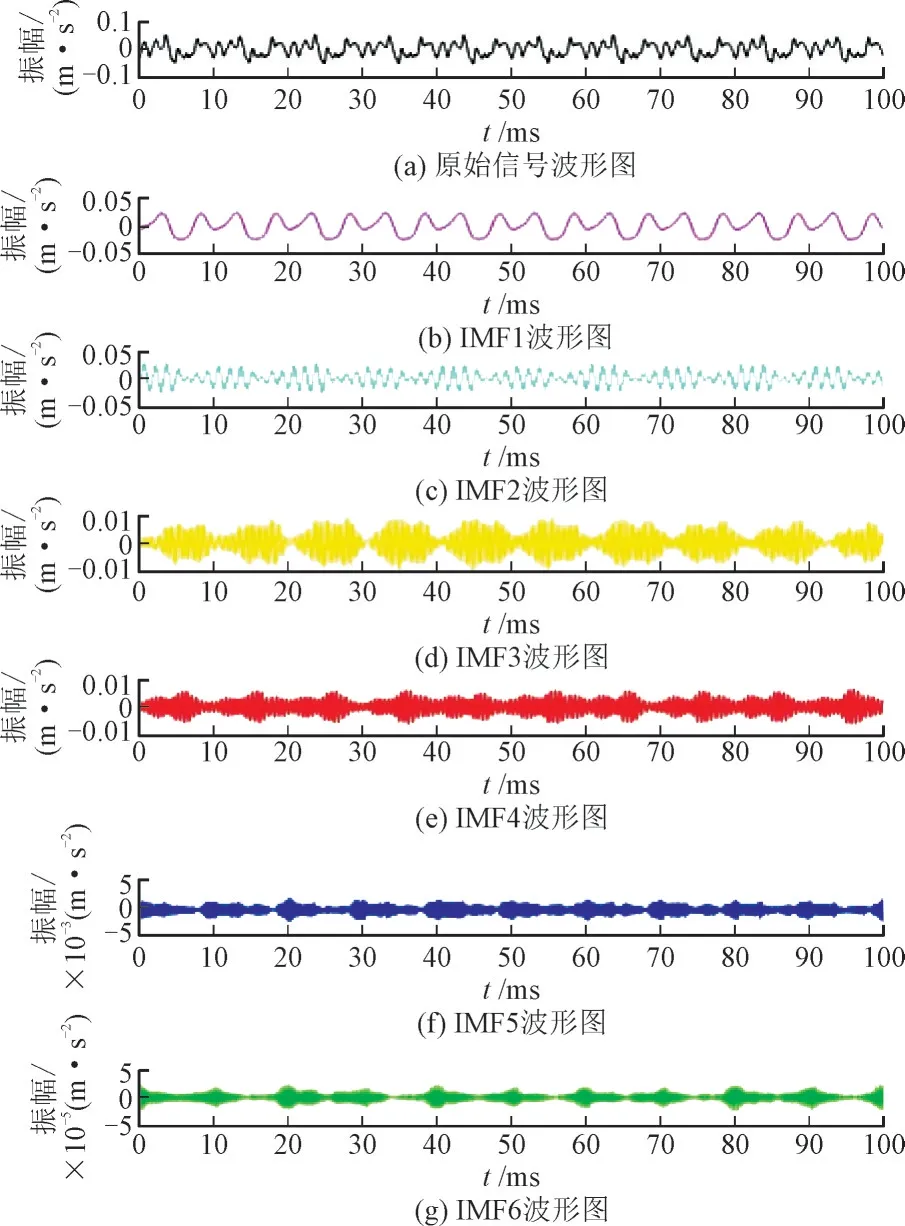
图5 原始信号及经VMD分解的模态分量的振动波形图Fig.5 Vibration waveforms of original signal and IMFs by VMD
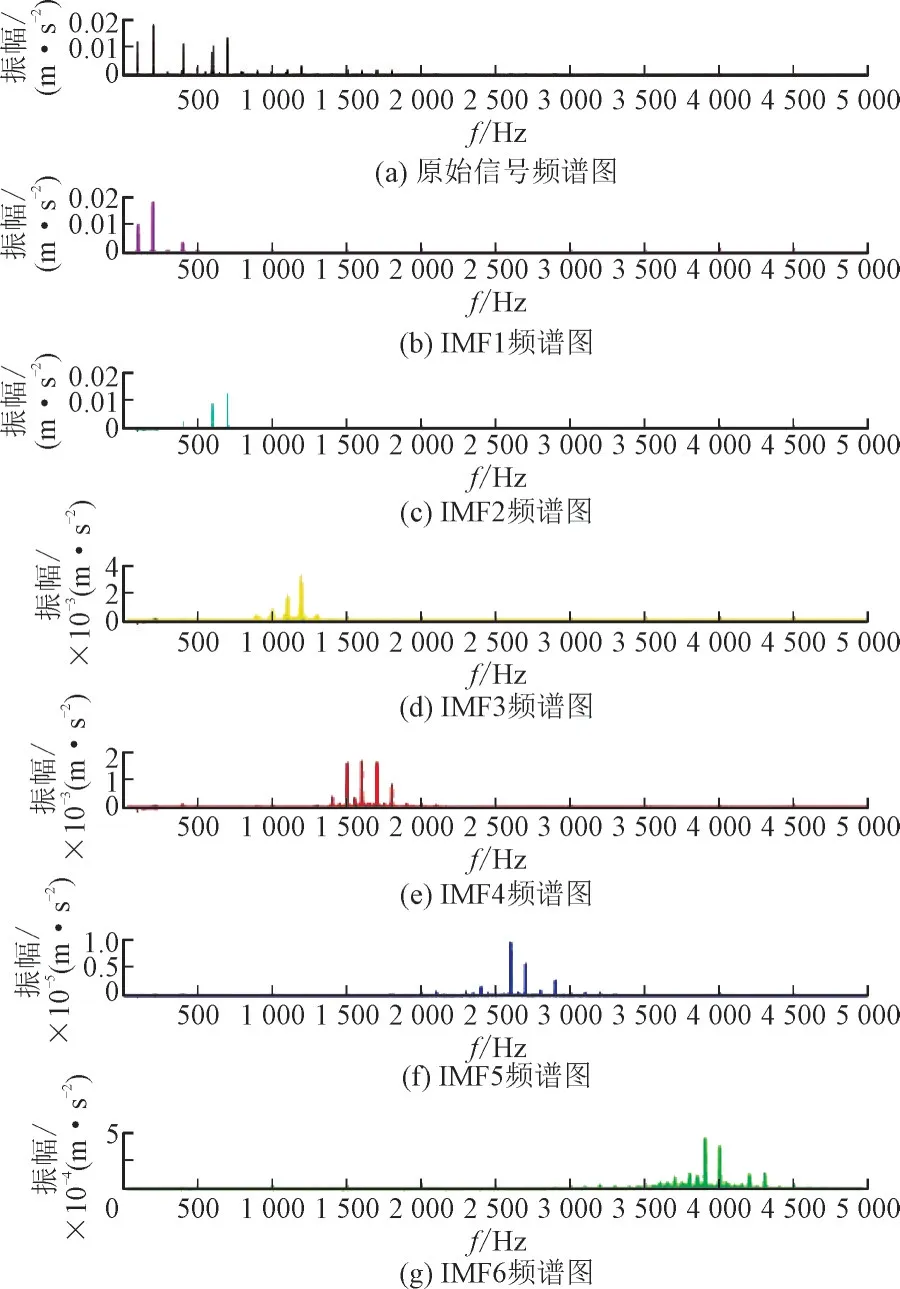
图6 原始信号及经VMD分解的模态分量的振动频谱图Fig.6 Vibration spectrum for original signal and IMFs by VMD
对原始信号和经VMD 分解的模态分量分别进行多尺度特征提取和特征归一化后,使用基于流形嵌入和动态分布对齐的领域自适应方法进行变压器状态识别实验,模型识别准确率如表5 所示。
由表5 可知,目标域测点和源域测点相距越近,状态识别准确率通常越高,其原因是受到变压器结构和电力磁力的影响,变压器的各部位振动特征各异,相距越近的测点可能测得分布越接近的振动数据,即振动的模态分量越相似,特征空间越相似。
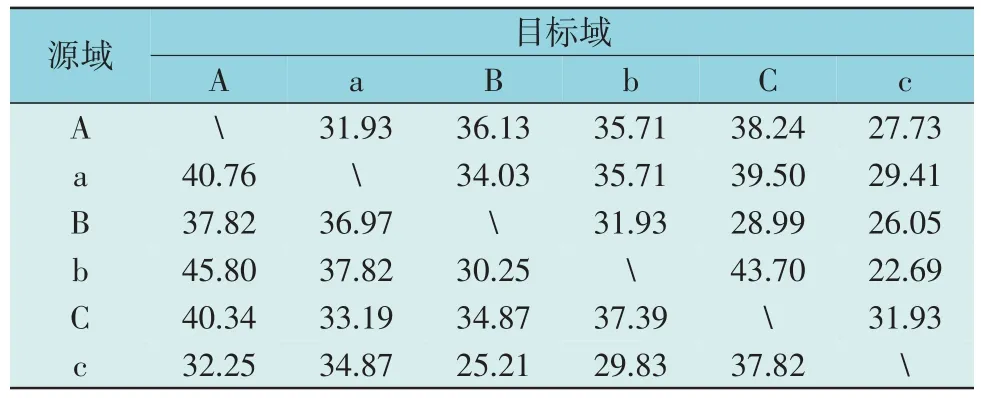
表5 所提模型状态识别准确率Table 5 Condition recognition accuracy of model %
每一迁移任务记作“源域→目标域”,表6 为对比实验的准确率结果。对比方法的参数设置为相关文献的默认值。
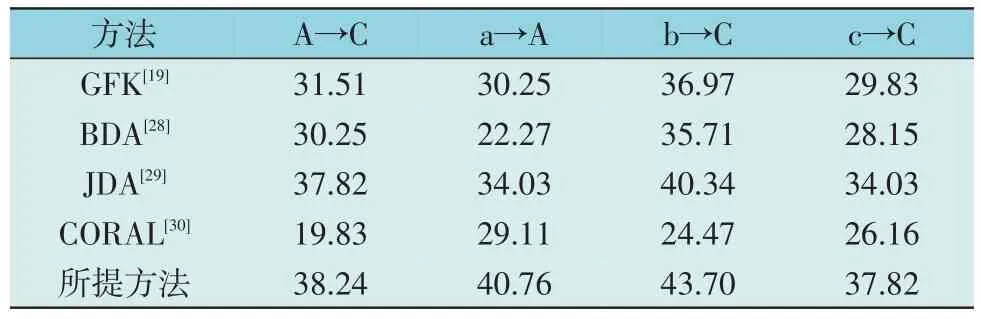
表6 对比实验准确率Table 6 Result of comparison experiments %
如表6 所示,在多个迁移任务中,所提方法对于变压器的状态识别准确率的负面影响高于其他算法,说明其在训练数据和测试数据来源不一、数据特征分布存在巨大差异的时候,能够在一定程度上缓解变压器状态识别模型泛化能力不足的问题。所提的方法能够减少领域偏移的负面影响,动态量化不同来源数据的边缘分布和条件分布在状态识别中的重要程度。此外,在源域和目标域数据测点相近时(如a→A),所提方法的性能优势更明显,这主要是因为利用VMD 分解得到了振动信号中的相似模态,并对其进行多尺度的特征提取,构建得到了描述更全面、分布更相似的特征空间。
4 结语
为了应对基于人工智能的变压器状态识别模型在应用中存在着模型泛化能力不足的问题,利用领域自适应方法在提高模型泛化能力上的优势,建立了一种基于领域自适应的变压器状态识别模型,并且根据变压器振动信号蕴含信息复杂的特点,提出了使用信号分解并进行多尺度特征提取的特征方法。通过在变压器不同位置进行信号采集,得到了具有不同分布的振动数据,经过实验验证,基于领域自适应的变压器状态识别方法能够在一定程度上改善当前变压器状态识别模型泛化能力不足的问题。但由于变压器振动机理复杂,不同测点之间的数据分布差异十分巨大,在提高变压器状态识别模型的泛化性能方面仍有很大的改进空间。

