基于改进CNN-LSTM的电力系统宽频振荡辨识
赵 妍,孙 硕,柳 旭,聂永辉
(1.东北电力大学输变电技术学院,吉林 吉林 132012;2.东北电力大学电气工程学院,吉林 吉林 132012)
0 引言
新一代能源电力系统具有高比例可再生能源和高比例电力电子设备的“双高”特点。新型可再生能源发电与同步发电机、柔性交直流输变电与传统交流输变电有本质的区别,导致电力系统的动态特性发生了深刻变化,带来了新的稳定性问题[1]。在电力电子设备之间及其与电网之间相互作用引起的电气量随时间作周期性波动,且频率振荡在较宽的范围内变化的动态过程称为电力系统宽频振荡,振荡的频率从几Hz 到数千Hz[1]。近年来我国出现了多起与新能源发电和电力电子设备相关的宽频振荡事件[2-3]。宽频振荡已经成为影响电力系统安全稳定运行的新问题。
宽频振荡中多模式并存,且随源网方式变化而此起彼伏,兼受扰动强弱影响而可能处在线性或非线性主导的不同阶段[4],呈现了强非线性特征。实际的振荡频率与特征值分析结果相比将产生偏移,而且振荡频率会随电网运行方式及电力电子设备运行点的变化而变化[5],即出现频率漂移现象,表现出明显的时变特征。宽频带振荡信号的强非线性和强时变特性导致给宽频振荡参数的准确辨识面临前所未有的挑战。
目前关于电力系统振荡参数辨识最主要的方法是信号处理类方法,而且集中在对低频、次同步/超同步振荡方面。典型的有快速傅里叶变换(Fast Fourier Transform,FFT)[6-8]、Prony 变换[9-11]、希尔伯特黄变换(Hilbert-Huang Transform,HHT)[12-14]、同步压缩小波变换(Synchrosqueezing Wavelet Transform,SST)[15]以及各种方法的改进算法[16-17]。但是,每种方法都有其适用的范围和局限性。FFT 和Prony 变换只能用于线性平稳信号的分析。HHT 可以分析非线性非平稳信号,但其中的经验模态分解(Empirical Mode Decomposition,EMD)有模态混叠问题。SST 通过对传统时频谱进行重排,解决时频谱能量发散的问题,通过改变支撑区间来消除模态混叠,解决了EMD 模态混叠的困扰[16-17]。但SST 方法对于具有时变特点的强调频信号处理结果不理想。
智能电网的建设促进了电力系统的信息深度化,使之成为融合量测、通信的电力物理信息系统。信息的种类、结构和时间尺度存在多样化,并呈现出爆炸式增长趋势,海量信息能够为宽频带振荡问题的研究提供数据支撑[18]。基于人工智能的宽频振荡辨识方法将振荡检测问题建模为分类问题,将参数辨识问题建模为回归问题[18]。
卷积神经网络[19-21](Convolution Ceural Network,CNN)是一类包含卷积计算且具有深度结构的前馈神经网络。CNN 方法强大的自适应特征提取能力,可以很好地提取复杂的强非线性数据的特征,与宽频振荡信号的强非线性特征相匹配。长短期记忆网络[22-24](Long Short-Term Memory,LSTM)是一种时间循环神经网络,可以学习长期依赖信息。由于LSTM 具有记忆结构,可以挖掘前后数据之间隐含的时序关系,与宽频振荡信号的强时变特征一致。因此,本文引入CNN-LSTM 循环神经网络并对其改进,对宽频带振荡参数进行辨识。
1 改进CNN-LSTM的模型设计
模型设计中需要考虑3 个问题:(1)CNN 一般采用的是有监督学习网络,模态参数定阶困难;(2)在模型训练过程中,超参数的选择对模型的性能影响很大;(3)CNN 输出的特征矩阵与LSTM 输入的对接处理。为解决上述问题,对CNN-LSTM 的模型设计进行改进。
1.1 无监督网络学习的构造
为解决CNN 模态参数的定阶问题,需对其进行了无监督优化,n组单模态信号时域波形叠加后输出值为:

式中:t为时刻;φi为第i个单模信号相位;Ai为第i个单模态信号幅值;fi为第i个单模态信号率;λi为第i个单模态信号衰减因子。
损失函数E为:

式中:n为样本总数;y(ti)为第i个期望值;g(ti)为第i个输出值。
以损失函数E作为模型输出层的损失函数,不断调整网络权重和偏置量,其表达式为:
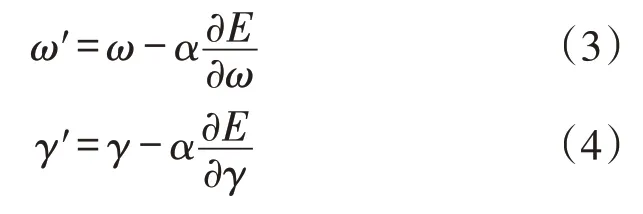
式中:ω,γ为当前网络权重和偏置量;ω′,γ′为调整后的权重和偏置量;α为当前网络学习率。
1.2 Nadam优化算法
在模型训练过程中,优化方法的选择对超参数的选择作用很大。随机梯度下降(Stochastic Gradient Descent,SGD)在模型优化的过程中没有引入动量的概念,导致其收敛速度慢,容易产生局部最优值。因此,在自适应动量估计(Adaptive Moment Estimation,Adam)中引入了一阶动量及二阶动量的概念。本文选择内斯特夫加速梯度(Nesterov Accelerated Gradient,NAG)作为一阶动量,其效果是使用累计梯度对当前梯度进行修正,即:

式中:gt为第t时间步的梯度;为梯度算子;J为目标函数;mt为t时刻的一阶动量;vt为t时刻的二阶动量。
NAG 利用了目标函数的二阶导数信息使得超参数随时间不断更新,保证了学习率的稳定更新。因此,本文选用NAG 与Adam 结合得到的Nadam 对学习率有更强的约束,实现更精确的辨识。
1.3 CNN模型与LSTM模型的连接
传统CNN-LSTM 模型对连接处理的方法是展开CNN 输出的特征矩阵,通过新生成矩阵维度的方式以符合LSTM 输入的格式。虽然这种展开的方法经实验仿真验证具有一定的有效性,但仍然不可避免地改变了对CNN 模型所输出的特征量[13]。
本文通过1×1 卷积运算代替LSTM 模型中W矩阵乘法,改进后结构见图1。其中cell 为当前模型状态,Conv 为卷积,Xt为输入向量,ht-1为输入时隐藏层状态,ht为输出时隐藏层状态,tanh为双曲正切函数。

图1 算法改进后LSTM结构图Fig.1 LSTM structure after algorithm improvement
根据图1,改进后的LSTM 模型将CNN 模型输出的特征向量Xt卷积为Xt*1×1,ht-1卷积为ht-1*1×1,其余过程不变。其中*1×1 代表1×1 卷积算子。
将输入Xt∈Rh卷积核和W∈Rr(其中r为卷积核个数,h为CNN 输出数据维数;W为CNN输出矩阵;Rh为元素为实数的h维空间集;Rr为元素为实数的r维空间集)的1×1 卷积运算,在文献[25]定义式为:

1×1 卷积运算代替LSTM 中的矩阵乘法。首先,在网络范围内的振荡数据和权重矩阵之间执行矩阵乘法将不可避免地会混淆不同时间片段的语义信息。而1×1 卷积实现了元素级的特征扩展,适合处理时变数据。其次,采用1×1 卷积算子减少矩阵乘法所需的参数数量,使得部署更加灵活。
2 改进CNN-LSTM模型搭建
参数辨识模型的总体流程如图2 所示。

图2 改进CNN-LSTM流程图Fig.2 Flow chart of improved CNN-LSTM
具体说明如下:
1)对CNN 进行无监督构造,省去标签量设定。输入训练数据,通过卷积层和池化层压缩数据的数量,提取振荡特征,并减小过拟合。全连接层可以汇总并输出特征数据集M。
2)数据集M通过Sigmoid 函数映射分类,对模态数量进行确定,实现对LSTM 的定阶。
3)输入数据集M,利用1×1 卷积运算替换LSTM 中矩阵乘法,通过LSTM 挖掘M的时间序列信息,获得其内部的变化规律,得到振荡参数辨识模型。最后输出LSTM 辨识结果ht,即输出每条振荡的频率及衰减因子。
通过Nadam 优化算法,得出LSTM 学习率为0.002 2。设置迭代步数为1 000。改进CNN-LSTM 网络结构见表1。其中模型损失函数为交叉熵损失函数,激活函数为RELU,优化器为Nadam,遗忘率为0.2。

表1 改进CNN-LSTM结构及参数Table 1 Structure and parameters of improved CNNLSTM
3 模型性能分析
3.1 振荡模态数量对辨识准确率的影响
训练数据采用仿真生成及部分实测数据。仿真信号由式(1)表示,将各模态参数进行自由组合,通过信号重构与叠加,可得到大量的宽频振荡信号。具体模态参数取值范围设为:频率为(0.1:0.1:1 000)Hz,衰减因子为-0.8:0.01:0.8。
采样频率为2 048 Hz,仿真时间为10 s。从生成的随机数据中选取4 000 条,构成仿真数据集T。通过交叉验证的方式寻找适合本文实际场景应用的训练集、验证集以及测试集。基于数据集T对模型进行训练,由于数据量较大,采用分批量训练方法进行。
在测试集中,取模态个数分别为1,2,…,12 的样本,进行频率和衰减因子准确率的比较。结果如图3 所示。

图3 不同模态数量的参数辨识准确率Fig.3 Accuracy of parameter identification with a different number of modes
由图3 可知,对不同模态层数,频率辨识误差在±1%以内、衰减因子误差在±2%以内。说明本文模型在一定范围内,精度几乎不受模态数量的影响,具有良好的鲁棒性。
3.2 优化算法对模型性能的影响
采用平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Squared Error,RMSE)、平均相对差(Mean Relative Error,MRE)及拟合优度R2作为评价标准。统计Adam,SGD 和Nadam 这3 种优化模型在测试集上的相关指标,见图4。3 种优化算法在训练过程中损失函数的变化趋势,见图5。

图4 3种优化算法对应的模型性能Fig.4 Model performance corresponding to three optimization algorithms

图5 3种优化算法在训练过程中的损失函数Fig.5 Loss function of three optimization algorithms in training process
由图4 可知,Nadam 速度最快,耗时仅用144.36 s,RMSE 与MAE 数值也最小,为1.809 与3.491。由图5 可知,SGD 算法训练速度慢且损失函数较大,在第401 步损失函数值为1.87。Adam 算法在比SGD 算法的速度提高,损失函数有所减小,在第310 步损失函数值稳定于1.46;Nadam 速度更快,损失函数更小,在第223 步损失函数值稳定于1.21。
3.3 模型连接方式对性能的影响
在相同优化算法下,分别构造模型1 与模型2并训练。模型1:CNN 与LSTM 模型连接方式采用1×1 卷积计算来代替深度学习网络中矩阵乘法。模型2:CNN 输出采用传统展开处理的方式再输入LSTM 模型。比较结果见图6。

图6 不同CNN与LSTM的连接方式的性能对比Fig.6 Performance comparison of different connection modes between CNN and LSTM
由图6 可知,改进后的CNN-LSTM 连接处理方式较传统CNN-LSTM 的连接处理方式,RMSE 和MRE 的数值均有小幅度下降,分别下降了0.127 与0.001,MAE 的数值下降明显,下降了0.471,R2有小幅度提升,上升0.002。
4 实例分析和验证
4.1 改进CNN-LSTM模型辨识结果
以西部某系统发生宽频振荡量测的35 kV,A相电压实测数据作为模型输入。录波结果见图7,采样频率为12.8 kHz,持续时间为60 s。

图7 录波结果Fig.7 Results of wave recording
对实测数据进行分批次输入,同时令改进CNN-LSTM 模型每隔5 s 输出,5 s 内批次分析结果,辨识结果见表2。
根据辨识结果,实测数据中含有6 种频率的模态分量。其中模态1 为次同步模态,模态3 为超同步模态。将模态1 和模态3 的频率和衰减因子绘制在图8 和图9 中。

图8 模态1和模态3的振荡频率Fig.8 Oscillation frequencies of mode 1 and mode 3

图9 模态1和模态3的衰减因子Fig.9 Attenuation factors of mode 1 and mode 3
次同步模态1,频率在19.8~20.7 Hz 范围漂移,超同步模态3 频率在79.4~80.4 Hz 范围漂移。这与事故后分析结果一致。
根据表2 和图9,两种振荡在15~50 s 为发散振荡,在50 s~60 s 这两个模态的衰减因子都变化到0附近。这与图7 实测信号先发散后持续接近等幅振荡的特点一致。

表2 改进CNN-LSTM的辨识结果Table 2 Identification results of improved CNN-LSTM
4.2 与SST方法的比较
选择Morlet 小波作为基函数。SST 的时频谱和分解结果如图10 和图11。图11 中仅列出两个固有模态分量(Intrinsic Mode Type,IMT)的标么值,即IMT1 和IMT3。图12 和图13 是IMT3 的频率和衰减因子辨识结果。

图10 SST时频谱Fig.10 SST time-frequency spectrum

图11 SST的分解结果Fig.11 Decomposition results of SST

图12 IMT3的频率辨识结果Fig.12 Frequency identification results of IMT3
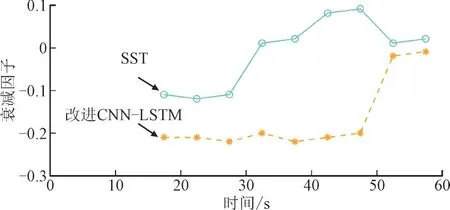
图13 IMT3的衰减因子辨识结果Fig.13 Identification results of attenuation factor of IMT3
由图10 可知,SST 的频率分析结果较理想,信号中含有6 种模态分量,在15 s 时出现了次/超同步振荡,与本文方法分析结果一致。图12 的分析结果也证明了这个结论。但是,图10 中无法观察到频率漂移现象。
图13 的衰减因子的辨识结果和本文方法相比出现了比较大的差异。SST 出现了模态混叠,导致辨识的衰减因子较大出现误差。
4.3 与CNN,CNN-LSTM和PNN-LSTM的比较
在Nadam 优化算法下对CNN 模型、CNNLSTM 模型、PNN-LSTM(Probabilistic Neural Network,PNN)模型及本文改进CNN-LSTM 4 种方法进行实验对比。
4 种方法的隐层设置如下:PNN-LSTM,PNN 模型为3 层,隐层神经元个数分别为600,200,100。LSTM 与改进CNN-LSTM 中LSTM 部分相同。CNN-LSTM 模型结构与改进后一致。CNN 模型与改进后CNN-LSTM 模型中CNN 部分相同。
对20~40 s 的实测数据分别单独采用CNN,CNN-LSTM 和PNN-LSTM 进行参数辨识,结果见表3。
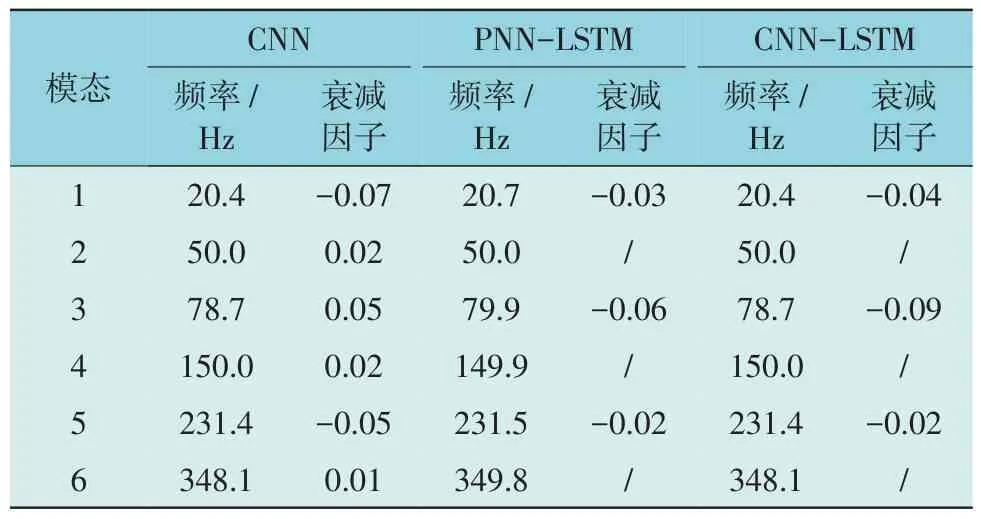
表3 3种方法的辨识结果Table 3 Identification results of three methods
CNN 模型可以有效辨识出各频率模态,但衰减因子结果与本文方法(表2)结果相差较大。这是由于CNN 在进行回归性问题处理时,丢失了大量数据间的联系,其结果是将特征相同但彼此间联系不同的特征错误回归,导致具有时变特征的衰减因子无法正确辨识,出现较大误差。CNN-LSTM 辨识结果优于单独CNN,说明了CNN 和LSTM 结合的必要性。
对PNN-LSTM,CNN-LSTM,改进CNN-LSTM 3种模型预测能力进行二次评判,损失函数衰减对比见图14。

图14 三种模型的损失函数衰减对比图Fig.14 Comparison of loss function attenuation between three models
由图14 可知,改进CNN-LSTM 与CNN-LSTM收敛速度较快,分别在在第211 个迭代步数及220个迭代步数达到稳定值,而PNN-LSTM 在第387 个迭代步数使损失函数达到稳定值,这证明改进CNN-LSTM 与CNN-LSTM 收敛速度明显优于PNN-LSTM 模型,模型泛化能力更好。
5 结论
1)改进的CNN-LSTM 充分利用CNN 处理强非线性数据的优势和LSTM 对时序数据敏感性的特点,成功辨识了宽频振荡的频率和衰减因子。在处理频率漂移现象和衰减因子突变等问题上有突出的优势。
2)无监督网络的构造使模型摆脱对数据标签的依赖,可以自动发现数据中潜在的结构,弥补前期标注数据不足的问题。Nadam 优化算法在传统自适应的改进使得模型超参数的选择具有最优效果。1×1 卷积运算实现了元素级特征扩展,避免改变CNN 层输出特征向量,非常适合处理时序性数据。
3)CNN 输出的特征数据集,输入LSTM 后,仍然需要部分标签数据,Softmax 分类器的准确分类确定了LSTM 模型所辨识参数的具体模态数,解决了模态参数定阶问题。

