例谈高考复习中的函数图象问题

陆容花

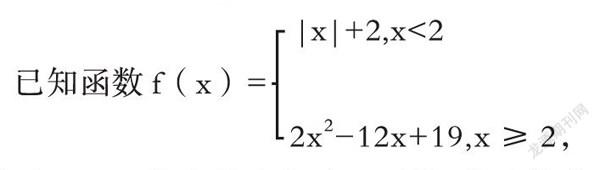
函数的图象是函数的一种表达形式，它形象地揭示了函数的性质，为研究函数的数量关系提供了“形”的直观性。而函数贯穿整个高中数学，是高考考查的重点内容，所以能够熟练解决关于函数图象问题显得尤为重要。下面通过对在高考复习中遇到的相关题目提出几点见解，希望能给广大高中学生解决函数图象问题提供帮助，培养学生的数形结合的思想，提高学生的数学解题能力，提升学生的数学核心素养。

一、夯实基础是关键

大部分学生对函数题望而却步，看到函数图象更加无所适从，其实最重要的一个原因是基础不牢固。所以要想解决这个问题，关键还是要夯实基础，对常用的几种初等函数的图象与性质熟练掌握。除了初中学习的一次函数与二次函数外，在新高考的数学必修第一册，还包含了幂函数、指数函数、对数函数和三角函数。所以学生在高一学习函数的时候一定要打好基础，对于上述提到的几种基本初等函数的图象会熟练准确地画出来，才能在高三复习的时候灵活运用。

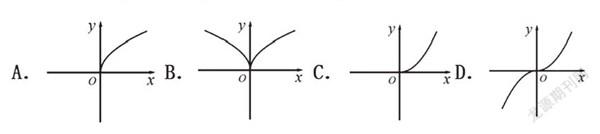
例1.已知函数f（x）=ax-4+1（a>0，且a≠1）的图象恒过定点P，若定点P在幂函数g（x）的图象上，则幂函数g（x）的图象是（    ）

【分析】本题主要考查了指数函数与幂函数的图象与性质，属基础题。先确定P点，再求幂函数解析式，最后确定选项A.

二、灵活应用是保障

1.图象的识别

函数中图象的识别是当前高考的热点，一般是给出函数的解析式，然后从选项中选出哪个图象符合给出的解析式。这种题方法比较灵活，对学生的解题能力要求比较高。但是如果掌握了方法，其实也不难。

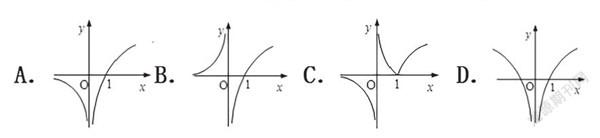
例2.函数f（x）=log2|2x-1|的图象大致是（     ）

【分析】将函数y=f（x）表示为分段函数，判断函数y=f（x）的单调性与该函数在（-∞，0）上的函数值符号，利用排除法可得出正确选项。

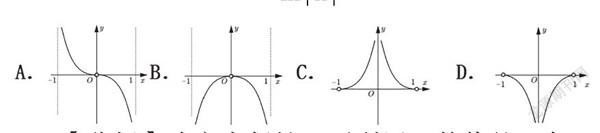
例3.函数f（x）=           的图象大致为（    ）

【分析】确定奇偶性，再利用函数值的正负，与变化趋势，排除三个选项，得出正确答案B。

方法总结：识别函数图象问题时首先关注定义域，然后从以下几个方面去研究函数图象：

（1）从图象的最高点、最低点，分析函数的最值、极值;（2）从图象的对称性，分析函数的奇偶性;（3）从图象的走向趋势，分析函数的单调性、周期性。（4）从函数的特殊点，代入验证数值。

一般利用以上几个方面，再根据排除法，则很容易选出正确选项。

2.画出具体函数的图象

在解决有些函数的题目中，需要作出根据题目给出的函数的图象，主要是利用基本初等函数图象或函数图象变换作出所需图象，然后根据图象研究函数的性质。学生除了对基本初等函数的图象要熟悉外，还要掌握函数图像变换的一般规律如左右平移，上下平移，对称变换，翻折变换等等。

|x|+2，x<2

例4.已知函数f（x）=

2x2-12x+19，x≥2，

若方程f（x）-a=0的实根之和为6，则a的取值范围为（    ）

A.（1，3]      B.[1，3] C.（1，4]     D.（3，4）

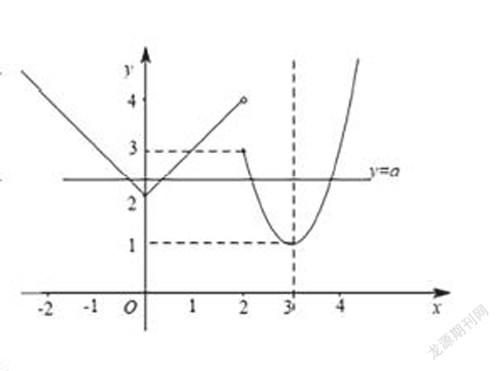
【分析】作出f（x）图象，求方程f（x）-a=0的实根之和为6，即求y=f（x）与y=a图象交点横坐标之和为6，分别讨论a=1、1<a<2、a=2、2<a≤3、3<a<4和a=4时y=a图象与y=f（x）图象交点个数及性质，数形结合，即可得答案.

【详解】作出f（x）图象，如图所示

求方程f（x）-a=0的实根之和为6，即求y=f（x）与y=a图象交点横坐标之和为6，当a=1时，y=a图象与y=f（x）图象只有一个交点（3，1），不满足题意;当1<a<2时，y=a图象与y=f（x）图象有2个交点，且从左至右设为x1，x2，由图象可得x1，x2关于x=3对称，所以

=3，即x1+x2=6，满足题意;当a=2时，y=a图象与y=f（x）图象有3个交点，且（0，2）为最左侧交点，设y=a与y=f（x）图象另外两个交点为x1，x2，由图象可得x1，x2关于x=3对称，所以       =3，即x1+x2=6，满足题意;当2<a≤3时，y=a图象与y=f（x）图象有4个交点，从左至右设为x1，x2，x3，x4，由图象可得x1，x2关于x=0对称，所以x1+x2=0，x3，x4关于x=3对称，所以         =3，即x3+x4=6，满足题意;当3<a<4时，y=a图象与y=f（x）有3个交点，由图象可得不满足题意;当a=4时，y=a图象与y=f（x）有2个交点，由图象可得不满足题意.综上：a的取值范围为1<a≤3.故选A。

方法总结：解题的关键是熟练掌握常见函数图象的作法，并灵活应用，处理函数零点问题时，常转化为图象交点横坐标问题，数形结合求解，即可得答案。

3.根据实际问题作函数图象

有些函数的题目会给出一个实际问题，然后让我们根据实际问题作出相应的图象。要解决这种题，学生需要有一定的函数基础，其次，一定要认真审题，根据题意作出或选出正确的图象。

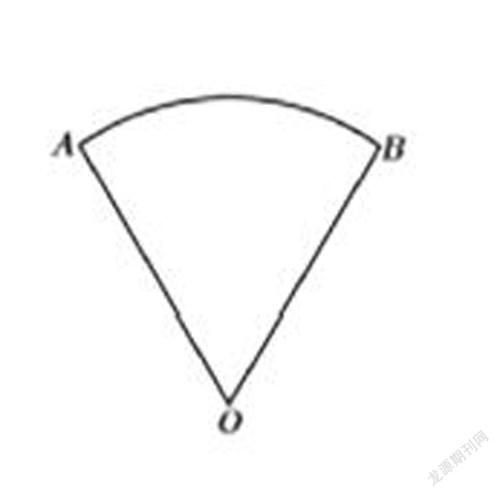
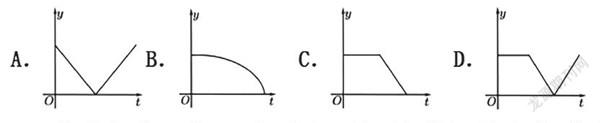
例5.如图，公园里有一处扇形花坛，小明同学从A点出发，沿花坛外侧的小路顺时针方向匀速走了一圈（路线为AB→BO→OA），则小明到点O的直线距离y与他从A点出发后运动的时间t之间的函数图象大致是（    ）

【分析】根据距离随与时间的增长的变化增减情况即可判定。

【详解】小明沿AB走时，与O点的直线距离保持不变，沿BO走时，随时间增加与点O的距离越来越小，沿OA走时，随时间增加与点O的距离越来越大.故选：D.

4.图象的应用

图象的应用主要是培养学生的数形结合的思想，通过对图形的分析和相关的运算，得出正确的结论。

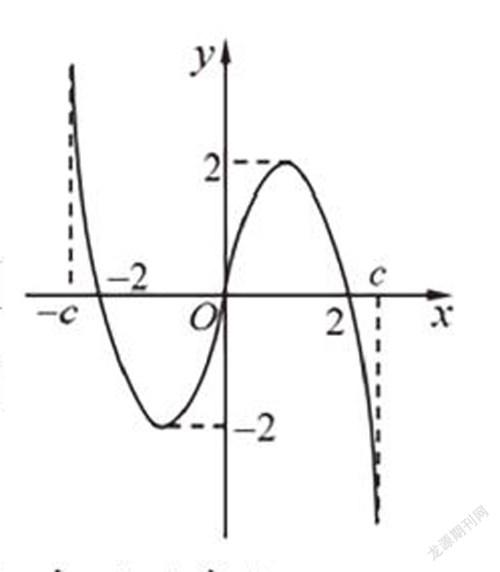
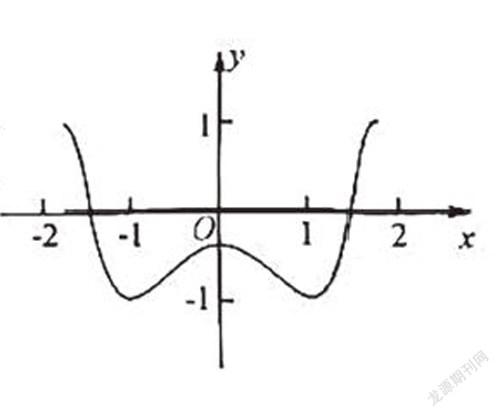
例6.（多选题）f（x）是定义在区间[-c，c]上的奇函数，其图像如图所示。令g（x）=af（x）+b，则下列关于函数g（x）的叙述正确的是（    ）

A.若a<0，则g（x）函数的图象关于原点对称

B.若a=-1，-2<b<0，则方程g（x）=0有大于2的实根

C.若a≠0，b=2，则方程g（x）=0有两个实根

D.若a≥1，-2<b<2，则方程g（x）=0有三个实根

【分析】根据函数图像及函数性質，数形结合，对选项一一分析即可得到答案BD.

5.根据函数图象选择解析式

根据函数图象选择解析式的方法也是从特殊值，从图象的对称性选择函数的奇偶性，图象的趋势等几方面去判断选择。

例7.已知某函数的部分图象大致如图所示，则下列函数中最合适的函数是（    ）

A.f（x）=sin（ex+e-x）

B.f（x）=sin（ex-e-x）

C.f（x）=cos（ex-e-x） D.f（x）=cos（ex+e-x）

【分析】根据特殊值排除A、C，再根据图象的对称性判断函数的奇偶性即可排除B;故选D.

总之，想要更好地解决函数的图象的问题，不仅要熟悉基本初等函数的图象和性质，还要懂得图象的变换，熟练运用数形结合的思想方法。面对函数的图象问题，我们要会画图，会识别图象，综合应用函数的图象和性质，就能比较容易准确地解决。

（责任编辑：张晓东）

3189501908219