新型双作用气浮气缸优化设计及其工况分析

钱鹏飞,罗辉,单位银,邹能祥,张兵

(1.江苏大学机械工程学院,212000,江苏镇江;2.宁波索诺工业自控设备有限公司,315000,浙江宁波)

气动技术是一种以压缩空气为工作介质来传递能量和信号的工程技术[1],而气缸是一种利用缸体前后气腔压差来驱动从动件完成直线、旋转、摆动运动的气动执行元件,具有结构简单、工作可靠、寿命长等优点,是气动系统中应用较为广泛的执行元件之一[2]。传统结构的气缸由于其摩擦力不可避免,在低速运动时容易产生时走时停的“爬行”现象,严重影响气缸性能[3]。除此之外,活塞与缸筒的摩擦还会对气缸本身造成一些影响,例如振动、发热等一系列问题。尽管研究气缸的摩擦特性建立精确的气缸摩檫力模型很有必要[4-6],但是从源头上掐断摩擦的产生会在精确的输出力控制方面有更直接的益处,因此开发新型的利用静压气体润滑原理的无摩擦气缸显得尤为重要。现在降低摩擦力这一层面,无摩擦气缸已经成为气缸发展的新趋势。

众多专家学者在无摩擦气缸方面做了大量的研究工作,例如,苏雅玲利用空气轴承的气浮原理设计了气体静压轴承式气缸[7];美国Airpot公司推出了Airpel-AB系列的无摩擦气缸;路波在其零重力悬挂系统中设计了一种气悬浮无摩擦气缸[8];孙建辉等针对无摩擦气缸抗侧向力不足的问题,提出了一种在活塞尾部增加环形卸压槽的新结构[9];朱晓在其高精度负载系统中通过Matlab数值仿真得到了无摩擦气缸的优化尺寸[10];刘昱利用粒子群优化算法对无摩擦气缸结构尺寸进行了优化[11],并且基于气浮无摩擦气缸构建气动重力补偿系统进行控制研究[12-14]。这些气缸都抛弃了传统的接触式密封,利用气体润滑原理实现了非接触式密封,但是这些气缸大多是单作用气缸,且其正常工作与否都受限于两腔的工作压力。

本文采用静压气体润滑技术构建出一种具有独立供气、独立排气的新型双作用气浮无摩擦气缸[15-16]。将气浮活塞相关尺寸参数以及供气压力设为变量进行Fluent仿真[17],观察其对气浮活塞的径向承载力及耗气量的影响。最后根据仿真结果得到较优的气浮活塞尺寸,并由此分析活塞-活塞杆组件在不同工况下的受力情况,得到了在相应工况下气浮活塞能正常运行的最小供气压力和最大外负载力与供气压力的关系式。

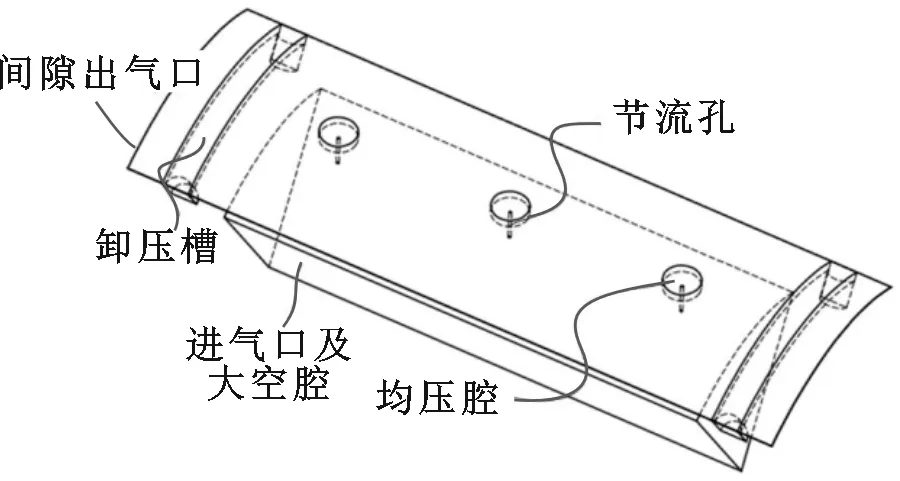
图1 气浮无摩擦气缸结构简图Fig.1 Structure diagram of air-floating frictionless pneumatic cylinder

1 新型气浮气缸的结构及其工作原理

基于静压气体润滑原理设计的新型双作用气浮无摩擦气缸的结构如图1所示。该气缸具有独立供气、独立排气、活塞自动调节对中等特点,其核心部件是特殊设计的气浮活塞。活塞表面设有多排周向均匀分布的节流孔,并在两端设有对称的环形卸压槽,整个活塞结构为一回转体;活塞与缸筒之间存在一定间隙,工作时在间隙内形成高压气膜实现无摩擦。

活塞与缸筒之间气膜的厚度,供气压力的大小,节流孔的个数、大小、排布及活塞长径比等参数都会影响无摩擦气缸的性能[18]。在安装过程中所产生的误差、活塞-活塞杆组件的重心在气缸中的位置随活塞的运动而改变等因素,都会引起缸筒与活塞中心线不平行,进而增大摩擦力造成磨损,因此新设计的气浮活塞工作时必须具备一定的径向承载力[19]。在满足所要求的承载条件下,该气浮气缸的设计目标是:①气浮活塞的径向承载力尽可能大;②耗气量尽可能小。由此,需要分析各个参数对径向承载力及耗气量的影响,为活塞结构参数优化设计以及合理选用提供参考。

2 基于Fluent仿真的优化设计

2.1 气浮活塞结构尺寸的设定

本文根据经验[7-8]选定的参数:活塞直径、长度分别为50、75 mm;均压腔直径为4 mm;均压腔深度与节流孔深度分别为1、4 mm;端面与卸压槽间距为5 mm;卸压槽深度与宽度分别为1、3 mm。本模型选取活塞结构为三排六孔,由研究经验可知,根据节流孔间距对活塞径向承载力的影响的变化规律是:随着节流孔间距逐渐增大,径向承载力先增大后减小。然而,由于气浮活塞的气浮特性受气膜厚度、节流孔径以及偏心量等参数的影响是相互耦合的,为了减少优化时间,本文根据经验[18]选取节流孔间距为20 mm,气膜厚度与节流孔径随仿真需要定义。

2.2 各参数对气浮活塞径向承载力及耗气量的影响

气浮活塞的径向承载力及耗气量受多个参数影响,主要有活塞与缸筒之间形成的气膜厚度h、活塞的偏心量e、节流孔径d与输入压强p等。本文通过仿真分析了这些参数对气浮活塞的径向承载力及耗气量的影响[17,20]。未经特殊说明,h=30 μm,e=5 μm,d=0.4 mm,p=0.4 MPa。

2.2.1 仿真前处理 气浮活塞的承载能力主要由压缩空气形成的高压气膜提供,因此仿真前需要建立气膜模型。对于无偏心的活塞,因其结构对称、周向形成的气膜厚度均匀,所以只需选取图2a所示的1/6模型进行网格划分与计算[21-22]。当活塞与缸筒之间产生偏心e时,因其气膜不再周向对称,所以采用如图2b所示的1/2模型进行网格划分与计算。

(a)1/6活塞流道模型

(b)1/2活塞流道模型图2 气浮活塞的流道简化模型Fig.2 Simplified model of the flow path of the air-floating piston

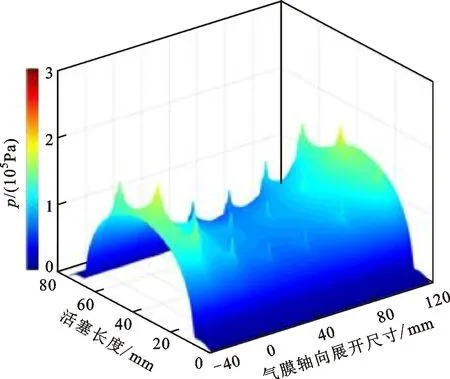
2.2.2 偏心量对径向承载力的影响 径向承载力是由于活塞轴线相对于缸筒轴线发生了偏离,有了偏心量e而产生的。为了更直观地看到偏心量对气浮特性的影响,通过控制其他参数不变,改变偏心量的大小进行仿真,得到图3所示的气膜周向展开压力分布图。

如图3a所示,在偏心量为0时,周向压力大致相等,仅在节流孔处稍有不同。随着偏心量e的增加,两侧压力的增加速度大于中间部分,形成压力梯度差,此为活塞径向承载力形成的原因。

图4给出了径向承载力随偏心量的变化。由图4可以看出,活塞径向承载力随偏心量的增加而增加,但活塞径向承载力的大小有一极限值。当活塞所受的合力大于活塞径向承载力的极限值时,活塞与缸筒会产生摩擦,影响活塞性能。

2.2.3 节流孔径与平均气膜厚度对径向承载力及耗气量的影响 因小孔节流结构简单便于加工,所以采用圆柱式小孔作为气浮活塞的节流孔。节流孔径d与平均气膜厚度h分别为小孔节流与薄层流动[23]对应的关键参数,这两个参数的变化直接影响气浮活塞的主要性能指标径向承载力。为了使径向承载力尽可能的大,即希望在较小的偏心量下具有较大的径向承载力,需要得到节流孔径d与平均气膜厚度h的内在联系。在保证其他参数不变的情况下,通过Fluent仿真研究节流孔对径向承载力的影响,给出了不同平均气膜厚度的径向承载力与耗气量随节流孔径的变化[24],如图5、图6所示。

由图5可清晰地看到,随着节流孔径d从0.1 mm增加到0.8 mm时,气浮活塞的径向承载力并不是单调递增的,而是出现一个峰值;且随着气膜厚度的增加,最优节流孔径这个峰值会前移。对图6来说,随着节流孔径的增加,其耗气量一直在增加;且随着气膜厚度的增加,其耗气量增长幅度也增加。

(a)e=0 μm

(b)e=5 μm

(c)e=10 μm

(d)e=15 μm

(e)e=20 μm

(f)e=25 μm图3 不同偏心量下的气膜周向展开压力分布图Fig.3 Air film pressure distribution under different eccentricity

图4 径向承载力随偏心量的变化Fig.4 Relationship between radial bearing capacity and eccentricity

图5 不同平均气膜厚度下径向承载力随节流孔径的变化Fig.5 Relationship between radial bearing capacity and orifice diameter for different average air film thickness

图6 不同平均气膜厚度下耗气量随节流孔径的变化Fig.6 Relationship between air consumption and orifice diameter for different average air film thickness

2.2.4 偏心量与供气压力对最优节流孔径的影响 为了研究偏心量的改变是否会影响最优节流孔径,将图5的条件中的偏心量e从5 μm改为10、13 μm,进一步仿真结果如图7、8所示。

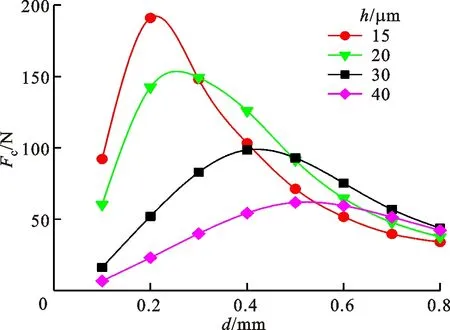
图7 偏心量为10 μm时不同平均气膜厚度下径向承载力随节流孔径的变化Fig.7 Radial bearing capacity versus orifice diameter for different average air film thickness at 10 μm eccentricity

图8 偏心量为13 μm时不同平均气膜厚度下径向承载力随节流孔径的变化Fig.8 Radial bearing capacity versus orifice diameter for different average air film thickness at 13 μm eccentricity

将图5、7、8进行对比可知,随着偏心量e的增加,最优节流孔径会减小。随后进一步研究偏心量的改变对耗气量的变化趋势有何影响,结果如图9、10所示,并将其与图6对比发现偏心量的改变对耗气量的变化趋势影响不大。

图9 偏心量为10 μm时不同平均气膜厚度下耗气量随节流孔径的变化Fig.9 Air consumption versus orifice diameter for different average air film thickness at 10 μm eccentricity

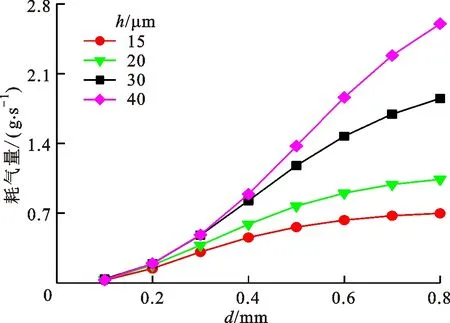
图10 偏心量为13 μm时不同平均气膜厚度下耗气量 随节流孔径的变化Fig.10 Air consumption versus orifice diameter for different average air film thickness at 13 μm eccentricity

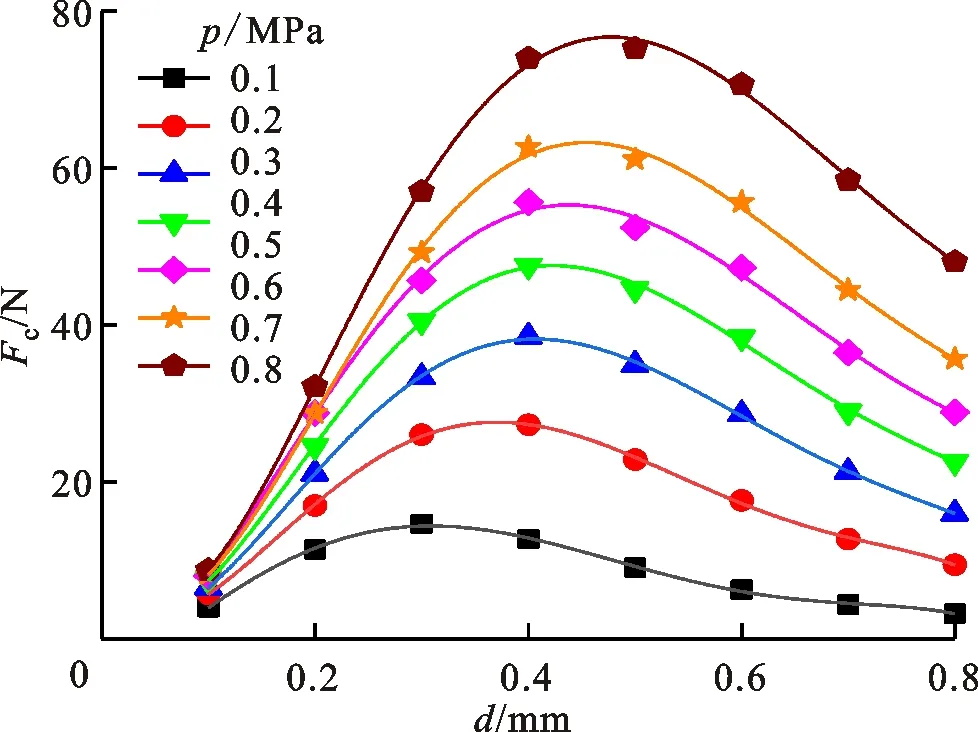
图11 不同供气压力下径向承载力随节流孔径的变化Fig.11 Relationship between radial bearing capacity and orifice diameter under different supply pressures

为研究供气压力的改变对最优节流孔径的影响,需要控制其他参数不变,改变供气压力进行仿真,得到如图11所示的不同供气压力下径向承载力随节流孔径的变化。由图11可知,随着供气压力的增加,除气浮活塞的径向承载力在增加外,其最优节流孔径也有所增加。因此还能通过实验室常用供气压力来进一步确定节流孔尺寸。

2.3 活塞尺寸的确定

由图5、6可以看出,根据不同平均气膜厚度的径向承载力与耗气量随节流孔径的变化可知,平均气膜厚度越小,其径向承载力越大,耗气量也越小。此外,结合经济性与现有加工水平进行综合考量,选用平均厚度为20 μm的气膜,其径向承载力足够且耗气量也可接受。最后通过对比偏心量与供气压力对最优节流孔径的影响,如图5、7、8、11所示,综合考虑选用直径为0.3 mm的节流孔。

3 活塞-活塞杆组件工况分析

本节主要针对于活塞-活塞杆组件进行工况分析,并通过仿真结果计算出所设计的活塞-活塞杆组件能够在缸筒中正常工作的最低供气压力及外加负载的最大值与供气压力的关系式。此工况分析可分为以下3种情况:①在不加活塞杆的条件下,仅考虑活塞自重,通过仿真结果确定使活塞始终悬浮的最小供气压力;②在①的条件下增加活塞杆,组成活塞-活塞杆组件,通过仿真结果计算出使活塞-活塞杆组件正常工作的最小供气压力;③在②的条件下,于活塞杆末端施加一个负载,通过仿真结果求得最大外负载与供气压力的关系式。

3.1 气浮活塞的力学分析

为得到承载力的最大值,需使偏心量尽可能地接近气膜厚度,因此选用偏心量为19 μm。考虑到实验室气泵的供气压力不能超过0.6 MPa,故选择气压为0～0.6 MPa进行仿真。根据仿真所得散点,采用多项式拟合绘制如图12所示的偏心量为19 μm时径向承载力随供气压力的变化曲线。同时得到供气压力p与径向承载力Fc的拟合关系式如下

Fc=55.7p2+418.31p-3.998

(1)

由于仿真得到的径向承载力为一标量,因此Fc需要大于0,由此可得适用于式(1)的供气压力范围为0.6 MPa≥p≥0.01 MPa。

图12 偏心量为19 μm时径向承载力随供气压力的变化Fig.12 Relationship between radial bearing capacity and air supply pressure at an eccentricity of 19 μm

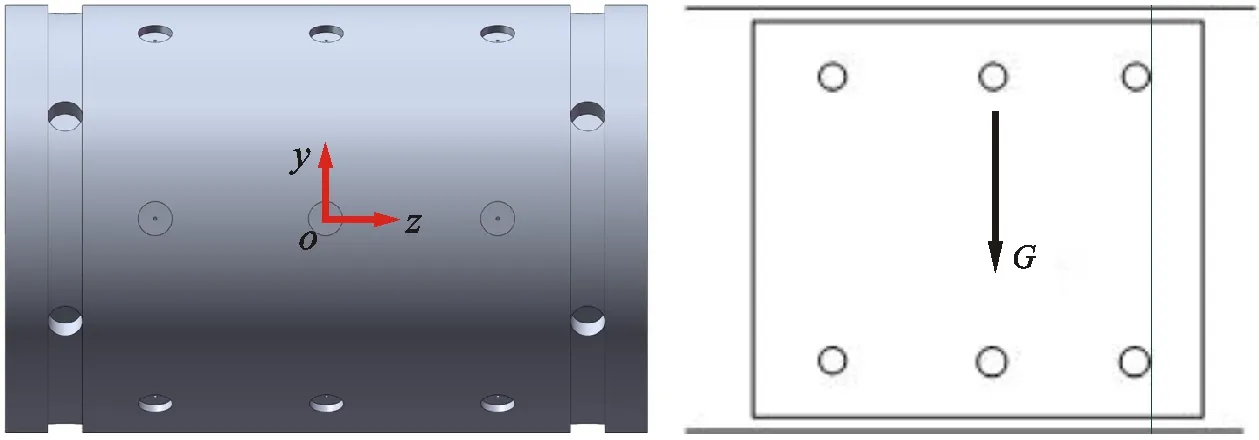
图13 活塞结构及其重心示意图Fig.13 Schematic diagram of the piston and its center of gravity

图13给出了活塞结构及其重心示意图,由于活塞整体结构对称,内部空腔、通道大致相同,因此其重心基本位于活塞中心。将活塞模型导入Solid works三维软件中,设定材料为铝合金7075,得出活塞重力为1.93 N。对于只考虑活塞自重这一条件,此时气浮活塞正常工作的径向承载力就应等于活塞重力。由式(1)可知,当径向承载力为1.93 N时,对应的供气压力约为14 kPa。因此,活塞始终悬浮于缸筒中,所需要的最小供气压力是14 kPa。

3.2 活塞-活塞杆组件无负载工况分析

根据活塞与缸筒尺寸所设计的活塞杆直径为8 mm,长度为565 mm;其中伸入活塞内部的杆长为65 mm,活塞外部的杆长为500 mm,将活塞杆的材料设定为45钢。图14为活塞-活塞杆组件结构重心示意图,经过测算,重心距活塞杆最左端约为415 mm,距活塞最右端约为160 mm。Solid works重心估算得出活塞-活塞杆组件总重力为4.03 N。为了分析活塞-活塞杆组件在无负载下正常工作所需的最小供气压力,将位于活塞杆端的空气轴承提供的均匀径向承载力简化为一个位于空气轴承中心且作用于活塞杆的力Fq,设定其始终能提供足够的径向承载力支撑活塞杆,且方向始终竖直向上。忽略气缸前端盖厚度,活塞-活塞杆组件的受力如图15所示。

图14 活塞-活塞杆组件及其重心示意图Fig.14 Schematic diagram of the piston-rod assembly and its center of gravity

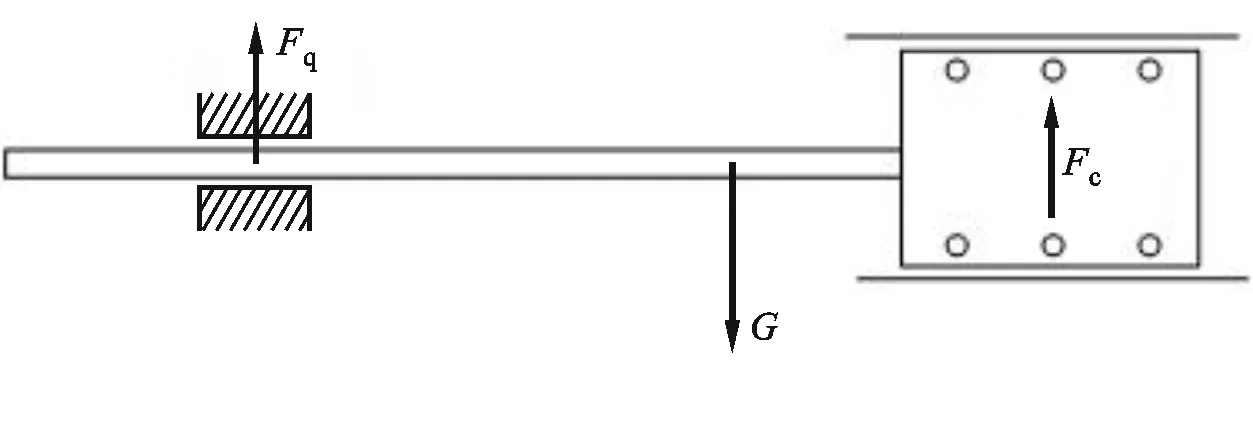
图15 活塞-活塞杆组件的受力示意图Fig.15 Schematic diagram of the forces on the piston-rod assembly

活塞-活塞杆组件在缸筒中的运动,重心的位置存在以下3种情况:重心介于空气轴承与活塞之间、位于空气轴承左边以及与空气轴承中心重合。为确保活塞-活塞杆组件能够正常工作,需对这3种情况进行分析,并通过对比计算后得到无摩擦气缸能够正常工作的最小供气压力。

图16给出了活塞-活塞杆组件重心介于空气轴承与活塞之间的情况。由力矩平衡可知[25],Fc的方向竖直向上。因为对于选定的活塞-活塞杆组件,其重心位置确定,所以将径向承载力Fc与重心G之间的固定距离L设为122.5 mm。将活塞-活塞杆组件重心与空气轴承中心之间的距离设定为变量x。以空气轴承为支点,可得如下力矩平衡方程

Gx-Fc(L+x)=0

(2)

变换式(2),并对x求导,可得

(3)

(4)

由式(4)可知,Fc随x的增加而增加,故当x最大时,Fc取得最大值,而当活塞运动到最右端时,此时x最大。由无摩擦气缸的设计尺寸可知,当活塞运动到最右端时,活塞杆左端距空气轴承中心为30 mm。所以此时x=385 mm,G=4.03 N。将G、L、x代入式(3),可求得Fc=3.06 N。根据式(1)可得此时供气压力约为17 kPa。

图16 活塞-活塞杆组件重心介于空气轴承与活塞之间时的受力Fig.16 Schematic diagram of the forces on the piston-rod assembly when the center of gravity is between the air bearing and the piston

图17 活塞-活塞杆组件重心位于空气轴承左侧时的受力Fig.17 Schematic diagram of the forces on the piston-rod assembly when the center of gravity is to the left of the air bearing

当活塞-活塞杆组件的重心位于空气轴承左侧时,根据力矩平衡得Fc的方向应竖直向下,其受力简图如图17所示。以空气轴承中心为支点进行受力分析,可得力矩平衡方程

Gx-Fc(L-x)=0

(5)

变换式(5),并对x求导,可得

(6)

(7)

由式(7)可知,Fc随x的增加而增加,故当x最大时,Fc能取得最大值。当活塞-活塞杆组件运动至最左端时x最大。由于忽略了活塞前端盖厚度,假设活塞左端与空气轴承右端重合,可得x=75 mm;将G、L、x代入式(6)得到Fc=6.3 N,再代入式(1)可得到此时供气压力约为25 kPa。

图18给出了活塞-活塞杆组件重心与空气轴承中心重合时的受力,空气轴承提供的径向承载力与重力平衡,此时Fc=0。

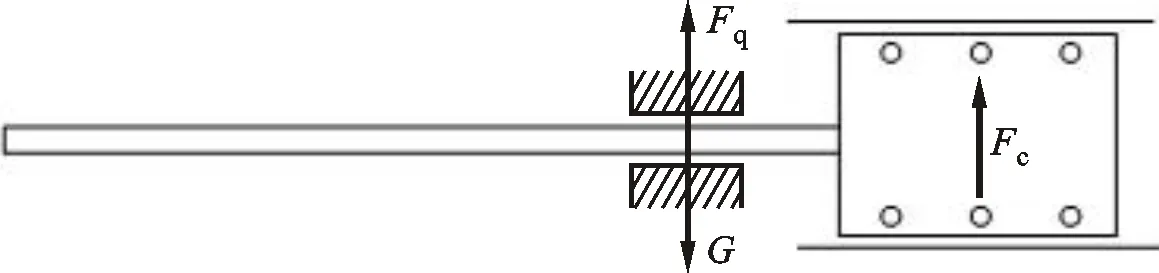
图18 活塞-活塞杆组件重心与空气轴承中心重合时的受力Fig.18 Schematic diagram of the forces on the piston-rod assembly when the center of gravity coincides with the center of air bearing

综上可知,活塞-活塞杆组件在缸筒中正常运动时的最低供气压力约为25 kPa。

3.3 活塞-活塞杆组件有负载工况分析

针对于在活塞杆末端增加负载这一工况,利用仿真结果计算无摩擦气缸能够正常运行的最大负载Fz;即研究活塞在最大供气压力下,活塞-活塞杆组件所能承受的最大负载,其中设供气压力最大值为pm。

图19给出了活塞-活塞杆组件重心介于空气轴承与活塞之间的受力,由力矩平衡可知,为使负载最大,需使径向承载力Fc竖直向下。

图19 加载情况下活塞-活塞杆组件重心位于空气轴承与活塞之间时的受力Fig.19 Schematic diagram of the forces on the piston-rod assembly when the center of gravity is between the air bearing and the piston under load

以空气轴承中心为支点进行受力分析,可得力矩平衡方程

Gx+Fc(L+x)-Fz(415-x)=0

(8)

变换式(8),并对x求导,可得

(9)

(10)

由式(10)可知,Fc随x的增加而增加。为保证气浮活塞在整个行程中都正常工作,需求在最大供气压力与最大偏心量的条件下,活塞运行过程中所能承受的最小负载Fz;故当x最小时,Fz能得到最小值。图20给出了重心与空气轴承中心重合时活塞-活塞杆组件的受力,此时x最小为0;最大供气压力为pm,与式(1)一同代入式(9)可得

(11)

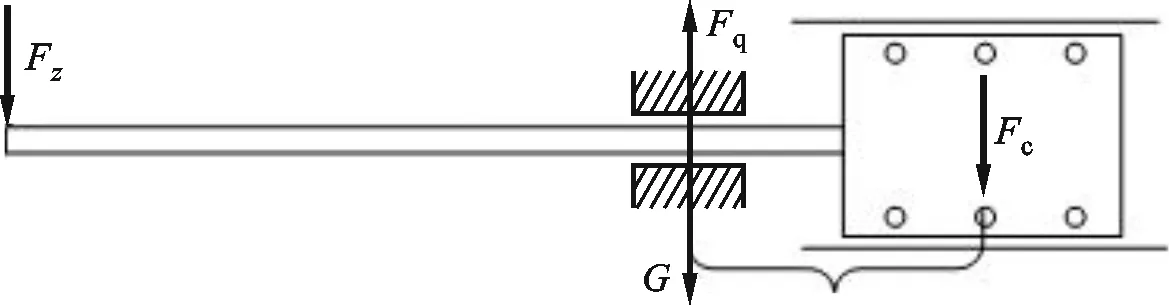
图20 加载情况下活塞-活塞杆组件重心与空气轴承中心重合时的受力Fig.20 Schematic diagram of the forces on the piston-rod assembly when the center of gravity coincides with the center of the air bearing under load

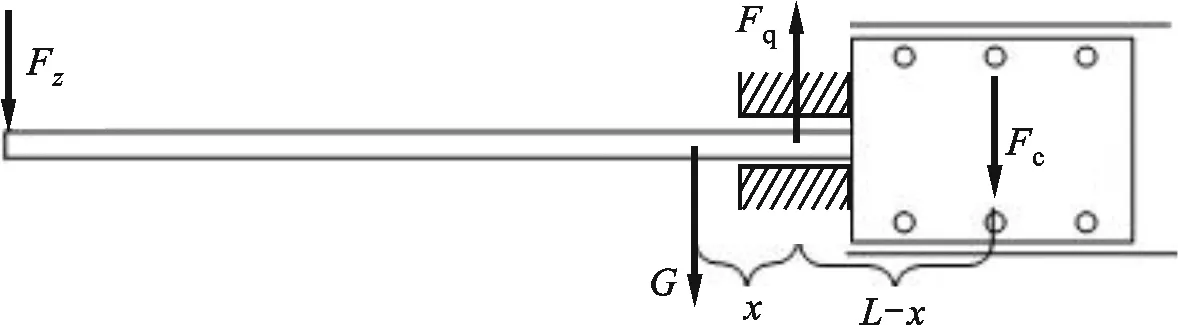
图21 加载情况下活塞-活塞杆组件的重心位于空气轴承左侧时的受力Fig.21 Schematic diagram of the forces on the piston-rod assembly when the center of gravity is to the left of the air bearing under load

图21给出了加载下重心位于空气轴承左侧时活塞-活塞杆组件的受力,根据力矩平衡可得Fc的方向竖直向下。对此以空气轴承中心为支点,可得力矩平衡方程

Gx+Fz(415+x)-Fc(L-x)=0

(12)

变换式(12),并对x求导,可得

(13)

(14)

由式(14)可知,Fz随x的增加而减小,故当x最大时,Fz能得到最小值。则当活塞-活塞杆组件运动至最左端时,x=75 mm;与式(1)一同代入式(13)中可得

Fz=5.399pm2+40.55pm-1.005

(15)

由于假定的供气压力范围为0.6 MPa≥p≥0.01 MPa,因此式(11)恒大于式(15),由此可得最大负载不能超过5.399pm2+40.55pm-1.005。

4 结 论

为使设计的新型双作用气浮无摩擦气缸拥有更好的静压气体润滑效果,利用仿真手段分析了偏心量、节流孔径与平均气膜厚度对活塞径向承载力及耗气量的影响,并从中得到了各气膜厚度下径向承载力最优的活塞节流孔径。此外,进一步研究了偏心量与供气压力对活塞最优节流孔径的影响,为活塞尺寸的选择提供理论依据。

利用仿真结果开展了不同工况下活塞-活塞杆组件在缸筒中非接触无摩擦运动时的受力情况分析,得出了气缸空载工况时最低供气压力、加载工况时最大外负载力与供气压力的关系式,为气浮活塞供气压力的确定提供参考。