采用改进回归型支持向量机的滚动轴承剩余寿命预测方法

徐洲常,王林军,刘洋,蔡康林,陈正坤,陈保家

(1.三峡大学水电机械设备设计与维护湖北省重点实验室,443002,湖北宜昌; 2.三峡大学机械与动力学院,443002,湖北宜昌)

轴承是应用于机械设备的常见零部件,其运行状态直接影响机械设备的工作进程,因此需要采用轴承故障分析与诊断方法对其进行健康监测。近年来,基于模型和数据驱动的故障诊断方法被广泛应用于机械零部件的运行状态评估及性能退化趋势预测[1-3]。基于模型的方法是针对诊断对象构建特定模型来实现故障诊断和寿命预测。例如,Kundu等构建了一种基于主成分分析(PCA)的威布尔加速失效时间回归模型[4],用于预测轴承的剩余使用寿命。Motahari等采用最近邻算法改进距离评价方法并用于特征降维,筛选出最优时域特征进行故障分类和剩余寿命预测[5]。Meng等采用基于微分的经验模态分解方法处理振动信号,获取能表征滚动轴承运行状态的分形维数和谱参数,通过灰色马尔可夫模型来预测轴承剩余寿命[6]。数据驱动方法则是通过分析监测数据,探究数据变化与设备运行状态变化之间的联系,实现故障诊断和寿命预测。Lei等采用长短时记忆网络和卷积神经网络构建新的诊断模型,并用于风力发电机故障诊断中[7]。赵洪山等通过玻尔兹曼机和逐层编码网络方法挖掘出风电机组主轴承监测数据所包含的信息,利用所得信息评估主轴承的运行状态[8]。Yan等获取若干能够表征轴承的运行状态指标,并优化支持向量机(SVM)得到混合退化跟踪模型,通过各项指标与优化后的模型实现轴承运行状态准确评估[9]。Xue等通过Hilbert变换和深度卷积神经网络处理振动信号得到若干频域特征和时域特征,将所得特征输入到SVM中实现对旋转机械的故障诊断[10]。于震梁等利用卡尔曼滤波改进SVM,构建出新的轴承寿命预测模型,通过该模型和现有实验数据可得到轴承各时刻剩余寿命估计值[11]。

为了实现轴承剩余寿命的预测,学者们提取了大量的轴承特征指标,但是大部分特征指标并不能清晰地表征轴承的运行状态,导致所得模型的预测精度较差。在模型相关参数确定过程中,普通算法进行参数寻优时容易陷入局部最优。为了获取最优的轴承健康指标并确定最优模型参数,搭建具有高精度预测性能的模型,提出基于主成分分析与改进的回归型支持向量机(SVR)的滚动轴承剩余寿命预测方法。该方法通过提取轴承信号时域和时频域的多个特征向量,利用PCA方法将所得特征融合成一个综合特征指标,将所得指标构建特征向量集,用差分进化灰狼群算法(DEGWO)对SVR模型进行参数寻优,将特征向量集输入到优化后的SVR模型中进行寿命状态识别。滚动轴承实测振动实验结果表明,所提方法可以准确预测滚动轴承剩余寿命;所得的综合特征指标能清晰地表征轴承的运行状态的变化;改进后的DEGWO算法对SVR参数寻优效果优于灰狼群算法(GWO)和网格搜索算法(GSA)。

1 特征提取

1.1 时域特征指标提取

设备振动信号的时域指标会随着其运行状态的改变而改变,即可通过时域指标的变化表征设备性能的变化。为全面地反映轴承全寿命过程中的健康状态和退化趋势,本文选用若干对故障敏感的时域指标表征轴承的状态信息。根据大量国内外文献总结,峰峰值、均方根值、峭度、波形因子和裕度因子等时域指标对轴承的运行状态变化比较敏感,时域指标计算公式可见文献[12]。

1.2 时频域特征指标提取

利用集合经验模态分解(EEMD)[13]方法对信号x(t)进行处理后,可提取时频域特征指标

(1)

(2)

(3)

1.3 综合特征指标提取

PCA是数据降维方法[14-15],通过PCA方法可将时域特征指标和时频域特征指标融合成一个综合特征指标,具体步骤如下。

步骤1若有m种z维的特征指标,构建特征矩阵并标准化处理得X=[X1,X2,…,Xm]T,计算X的相关系数矩阵的特征值λi(i=1,2,…,m)并按降序排列,特征相互融合得到的综合矩阵为

F=[F1,F2,…,Fm]T

(4)

F=AX

(5)

式中:Fi为第i个特征值λi对应主成分;A为主成分系数矩阵,由与λi对应的特征向量ai构成。

步骤2根据特征值λi计算各主成分的贡献率

(6)

为了清晰地表征轴承的运行状态信息,需要提取大量的时域和时频域特征,这会带来维数灾难问题,进而影响轴承寿命预测的精度和效率。本文通过PCA方法将时域特征指标和时频域特征指标融合成归一化综合指标T,剔除那些隐藏在高维特征集中的不敏感的冗余特征量。T能更好地表征轴承运行状态,作为轴承状态变化评估指标。

2 SVR模型的构建与性能评估

2.1 回归型支持向量机

支持向量机是一种处理数据分类问题的方法,Vapnik等在SVM分类的基础上引入了不敏感损失函数ε,得到回归型支持向量机,解决回归拟合方面的问题,即可找到一个最优分类面使得所有训练样本离该最优分类面的误差最小。

回归函数f(x)表达式为

(7)

式中:αl为拉格朗日乘子;K(x,xl)为引入的核函数;b为偏置向量。

拉格朗日乘子αl通过下式求解

(8)

式中:C为惩罚参数。

考虑数据样本和参数的选定,本文使用径向基函数(RBF)核,其表达式为

(9)

式中:σ为待定核参数。

2.2 相关参数的调节

惩罚参数c和RBF核参数g的选取会影响SVR模型的建立以及预测性能。针对SVR模型中最优参数难以确定,且利用GWO算法进行参数寻优时容易陷入局部最优的问题,本文采用差分进化算法(DE)和GWO算法相结合,构成新的差分灰狼群算法(DEGWO)对SVR模型的参数进行优化。

Vk(t+1)=Yα(t)+W(Yβ(t)-Yδ(t))

(10)

(11)

Yk(t+1)=

(12)

式中:t为当前迭代次数;Vk(t+1)为目标变异个体中的第k个体;W为缩放因子;Uk(t+1)为中间个体;G为交叉概率;fs(x)为适应度函数。

2.3 预测模型的建立与性能评估

采用DEGWO算法改进SVR的滚动轴承剩余寿命预测方法的流程如图1所示,主要步骤包括:信号的采集和处理、特征指标的获取、实验数据集的构造、最优参数的确定、SVR训练和预测等。

图1 轴承剩余寿命预测方法的流程Fig.1 Flow chart of the proposed prediction method for residual life of bearing

为评估模型的预测性能,本文选用均方误差mse、相关系数p和决定系数r2为判据,分析并评估预测结果,其计算公式分别如下

(13)

(14)

(15)

3 滚动轴承寿命预测分析实例

本文选取IEEE PHM 2012数据集[18]为实验数据,该数据集通过加速退化实验获取滚动轴承从正常到故障的整个生命周期的实验数据,即3种不同工况下的17组轴承全寿命数据。工况1的电机转速为1 800 r/min,负载为4 000 N;工况2的电机转速为1 650 r/min,负载为4 200 N;工况3的电机转速为1 500 r/min,负载为5 000 N。其中工况1和工况2各包含7个轴承,工况3包含3个轴承。

本节实验中,取工况3下的3个滚动轴承为研究对象,分别记为轴承3-1、3-2和3-3。其中轴承3-3数据为主要实验数据,轴承3-1和3-2数据为验证数据。所使用的轴承数据由加速度计测量得到,其中轴承3-3的全寿命振动数据如图2所示。

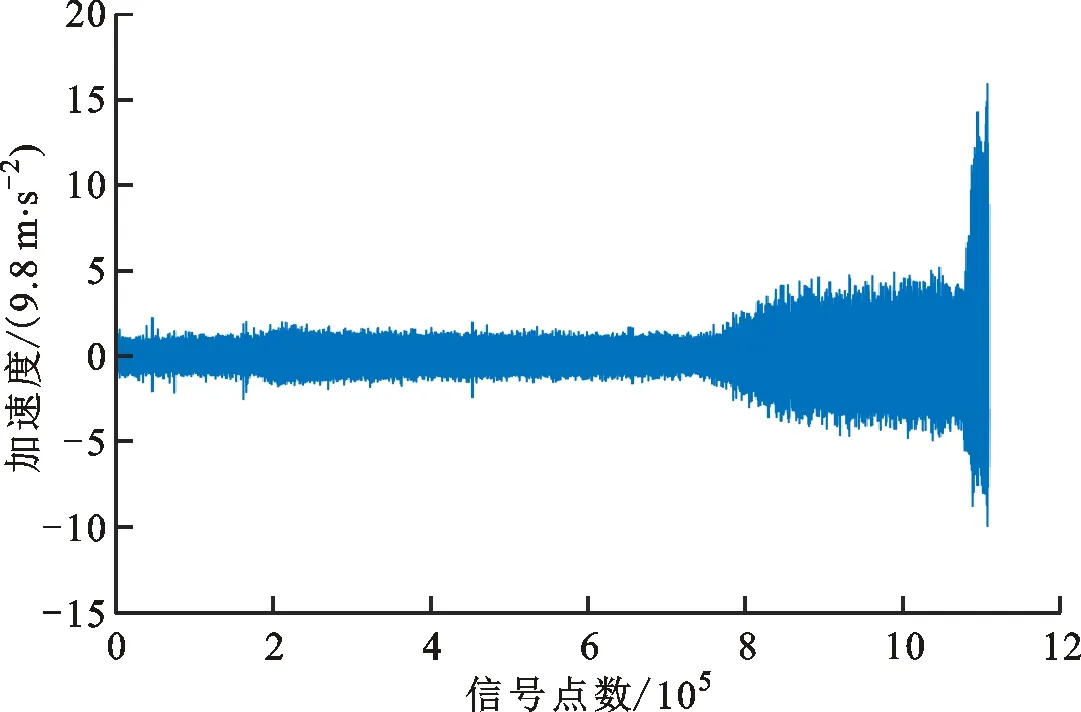
图2 轴承3-3的全寿命振动数据Fig.2 Full-life vibration data of bearing 3-3

为提高轴承状态描述能力,将轴承3-3的全寿命数据按点数均分,得到1 085个轴承信号序列数据,并对每段数据进行降噪处理。计算每段数据的若干时域指标,即峰峰值、均方根、峭度、波形因子和裕度因子5项指标,计算每段数据EEMD能量熵并归一化处理得到w3-3指标,轴承3-3的6项全寿命特征指标如图3所示。通过PCA方法将6项特征指标融合成一个如图4所示的归一化综合指标T3-3。由图4可知,T3-3能反映轴承性能变换,且大致可划分为4个阶段,如表1所示。分析表1和图4可知,在第1个阶段T3-3变化平稳,表征轴承正常运行,在该阶段T3-3出现一定的波动后趋于平稳,说明轴承度过磨合期之后性能又趋于平稳,从第2个阶段T3-3剧烈变化,到第3个阶段T3-3缓慢变化并恢复平稳,最后再到第4个阶段T3-3急剧跳动,它的变化对应轴承运行状态的变化,即轴承从出现故障到最终完全失效。分析图3、图4和表1可知,所得的6项全寿命特征指标和T3-3均能反映轴承3-3的性能变化,而w3-3和T3-3随着轴承运行状态的变化其值改变较大,故选用w和T作为可靠性指标评估轴承性能和运行状态;在全寿命阶段,T3-3的离散程度小于w3-3。

为验证本文方法的有效性,并确定最优可靠性评估指标,构建两类不同的预测模型并进行轴承寿命预测。

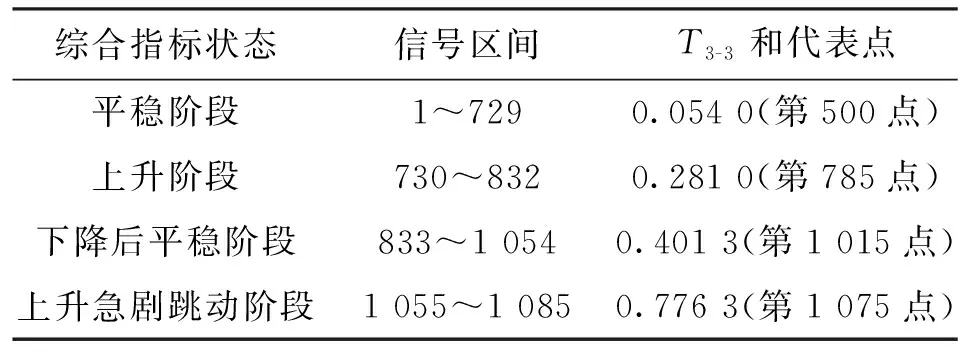
表1 T3-3的4个阶段

(a)峰峰值和均方根

(b)峭度和波形因子

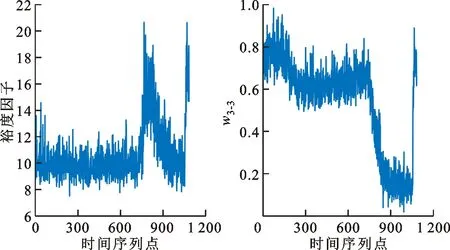
(c)裕度因子和EEMD能量熵图3 轴承3-3的6项全寿命特征指标Fig.3 Six characteristic indexes of full life of bearing 3-3

图4 轴承3-3全寿命归一化综合指标Fig.4 Normalized comprehensive index of full life of bearing 3-3

构建第1类模型,轴承运行状态评估指标为时频域指标w,训练样本为轴承3-3的前650组w3-3,预测样本为后435组w3-3。考虑迭代步长h,即前h个时段对当前时段机械运行状态的影响,令h=2,3,4,5,6,7。用DEGWO算法寻优确定参数c和g,搭建不同迭代步长下的SVR模型,模型输出为w3-3的预测值,不同模型的mse和r2见表2。由表2可知,随着h的增加,模型的mse先减小后又快速增大,而r2先增大后趋于稳定最终又快速减小。其中步长h=6模型的mse为0.003 8,r2为0.853 4,预测效果最优,将该模型记为模型1,预测结果如图5所示。由图5可知,输出预测值与实际值较为贴合,该模型能够评估轴承运行状态实现寿命预测。

表2 不同迭代步长下的模型预测性能的对比

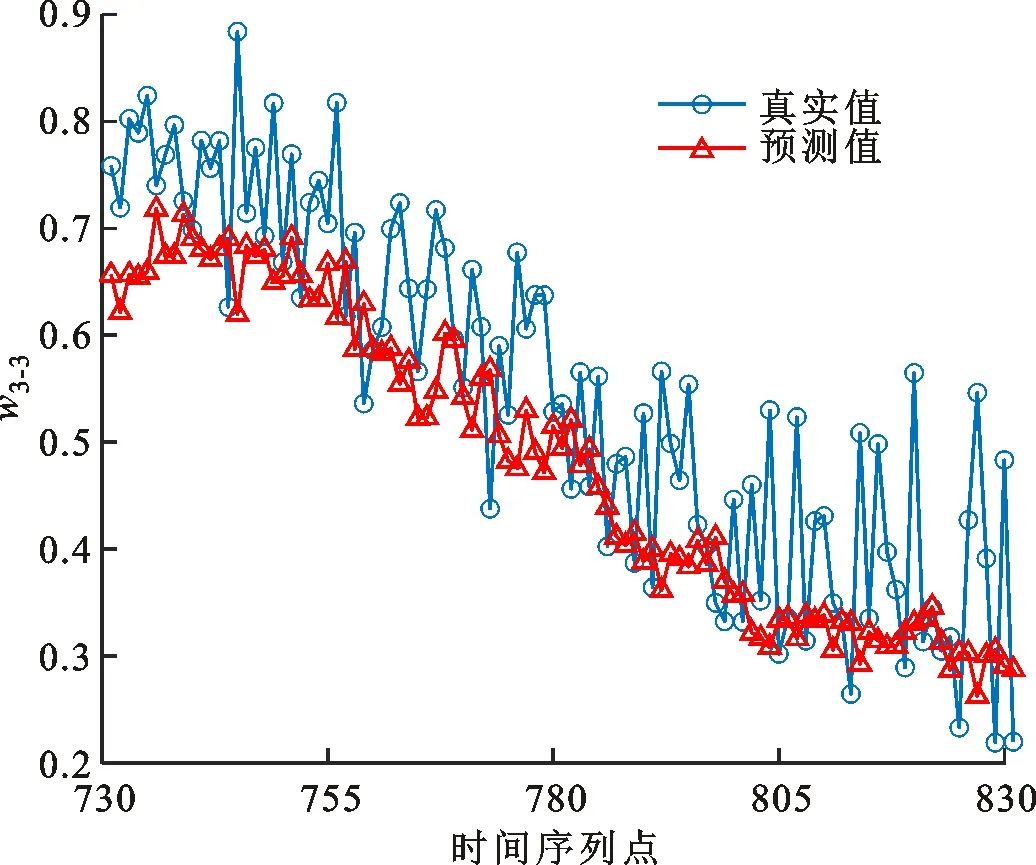
图5 第1类预测模型的预测结果Fig.5 Prediction results of the first type of prediction model

为展示第1类模型的预测结果,图5给出了轴承3-3第730段到第830段(出现故障的阶段)的运行状态评估指标的真实值和预测值。本文中其他几类模型的预测结果将按相同方式给出。

构建第2类模型,轴承运行状态评估指标为归一化综合指标T,模型的输入为轴承3-3信号的5维时域特征和1维时频域特征,输出为相应时间段的T3-3,前650组数据为训练样本,后435组数据为预测样本。用DEGWO算法确定最优参数c和g,搭建SVR模型进行轴承剩余寿命预测,第2类预测模型的预测结果如图6所示,记该模型为模型2。模型1和2的预测性能评估指标可见表3。对比图5和图6,并分析表2和表3可知,构建的两类SVR模型均能实现轴承剩余寿命预测;w3-3和T3-3均能表征轴承运行状态的变化,并用于轴承剩余寿命预测;与模型1相比,模型2的mse为0.003 0,下降了21.05%,p和r2分别为0.967 9和0.907 9,提高了2.39%和6.39%,故模型2的预测性能优于模型1;用综合指标作为状态评估指标所得预测模型,其预测性能优于用能量熵作评估指标的模型,即用第2类模型进行寿命预测效果更优。

图6 第2类预测模型的预测结果Fig.6 Prediction results of the second type of prediction model

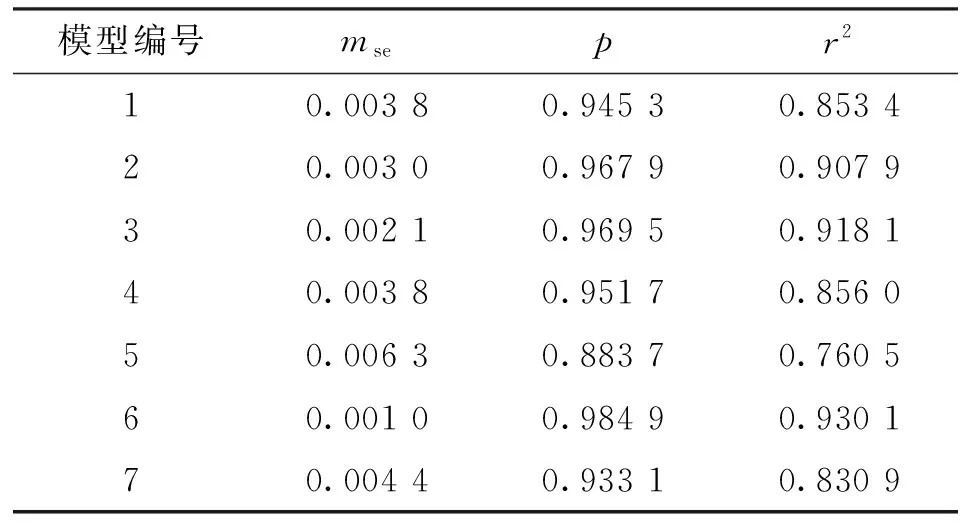
表3 不同预测模型的预测性能对比

轴承3-1全寿命数据如图7所示。将轴承3-1全寿命数据按点数均分为1 030段信号序列数据,计算每段数据的时域和时频域指标,PCA处理后得到如图8所示的轴承3-1全寿命归一化综合指标T3-1。由图8可知,T3-1能够表征轴承3-1性能变化。

图7 轴承3-1的全寿命数据Fig.7 Full life data of bearing 3-1

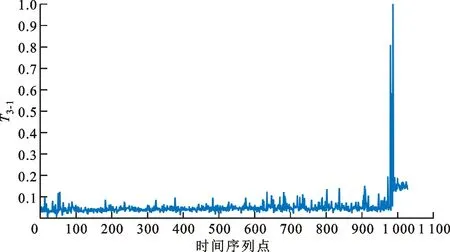
图8 轴承3-1全寿命归一化综合指标Fig.8 Normalized comprehensive index of full life of bearing 3-1

(a)DEGWO算法

(b)GWO算法

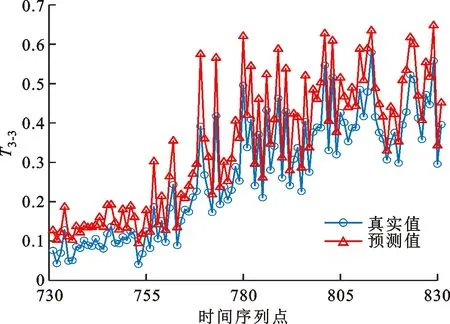
为进一步验证本文方法的有效性,并研究不同的优化算法对回归模型以及预测性能的影响,构建第3类预测模型。轴承运行状态评估指标为归一化综合指标T,模型的输入为轴承的5维时域特征和1维时频域特征,输出为相应时间段的综合指标,轴承3-1的全寿命数据为训练样本,轴承3-3的全寿命数据为预测样本,模型参数c和g分别通过DEGWO、GWO、GSA这3种不同算法寻优确定,搭建不同的SVR模型并进行寿命预测,模型预测结果如图9所示。3种不同优化算法所得的模型分别记为模型3、模型4和模型5,模型3～5预测性能的评估指标可见表3。分析图9和表3可知,第3类预测模型均能有效预测轴承剩余寿命,体现了所提方法和实验数据的有效性;在构建预测模型时,c和g可由不同优化算法确定,但是优化算法的选用会影响最终所得的SVR模型及其预测性能;与模型4和模型5相比,模型3的mse分别降低了44.74%和66.67%,而p分别提高了1.87%和9.71%,r2分别提高了7.25%和20.72%,充分说明DEGWO算法优化所得SVR模型的预测效果优于其他两种算法优化所得的SVR模型,即改进后的DEGWO算法对SVR参数寻优效果优于GWO算法和GSA算法。

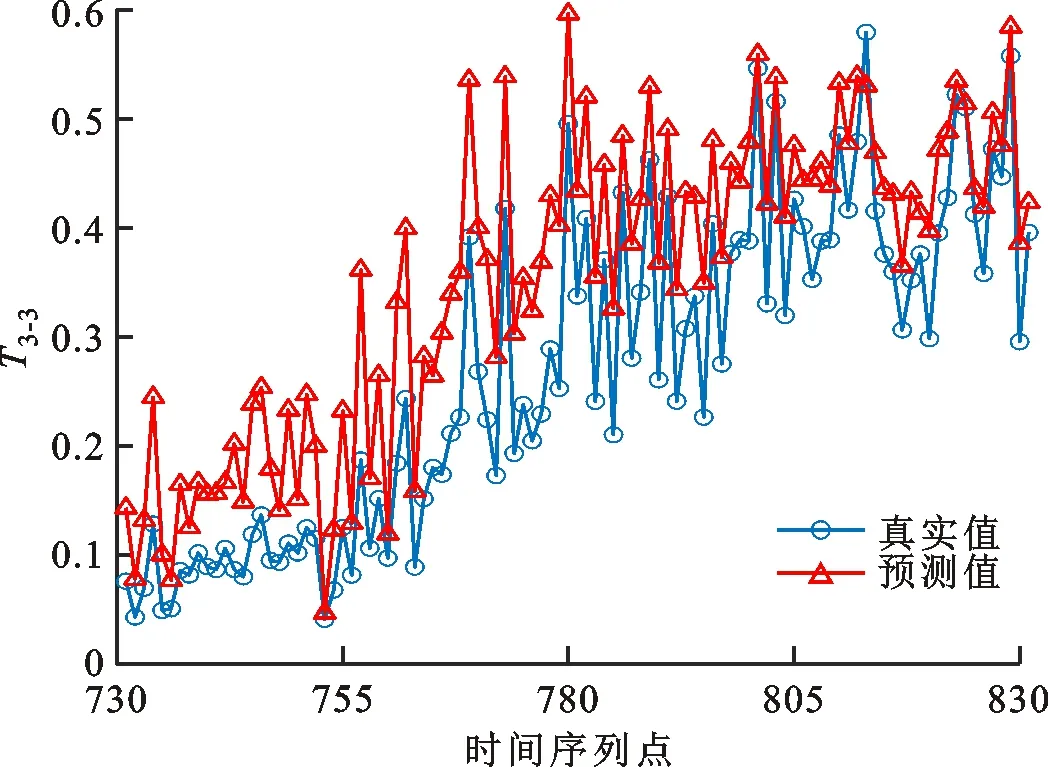
(c)GSA算法图9 不同算法的第3类预测模型的预测结果对比Fig.9 A comparison of prediction results for third type of prediction model

(a)DEGWO算法优化的SVR模型

(b)LSTM模型图10 第4类预测模型的预测结果对比Fig.10 A comparison of prediction results for fourth type of prediction model

为进一步验证本文方法的优越性,用处理轴承3-3的方法处理轴承3-2,得到表征轴承3-2性能变化的全寿命归一化综合指标T3-2(1 637个点)。构建第4类预测模型如下:轴承运行状态评估指标为归一化综合指标T,模型的输入为轴承的5维时域特征和1维时频域特征,输出为相应时间段的综合指标,轴承3-2的数据为训练样本,轴承3-3的数据为预测样本。用DEGWO算法确定最优参数c和g,搭建SVR模型进行轴承剩余寿命预测,记该模型为模型6,其预测结果如图10a所示;使用模型6的数据和指标,依据文献[19]构建长短期记忆神经网络(LSTM)预测模型进行轴承剩余寿命预测,记该模型为模型7,预测结果如图10b所示。模型6和7预测性能的评估指标可见表3。分析图10和表3可知,模型6和模型7均能实现轴承3-3剩余使用寿命的预测,但是与模型7相比,模型6的mse降低了77.27%,而p和r2提高了5.55%和11.94%,说明模型6的预测性能优于模型7。预测结果体现了所提方法和实验数据的有效性,验证了所提方法的优越性。

4 结 论

本文建立了若干个轴承剩余寿命预测模型,结合实测的轴承数据对标号3-3的滚动轴承进行运行状态评估与寿命预测,通过对比分析不同模型下的预测结果与性能,得出如下结论。

(1)对轴承全寿命数据分段处理并计算各段数据时域以及EEMD能量熵指标,利用PCA方法将所得特征指标融合成一个综合指标,所得的综合指标能够替代时域指标和EEMD能量熵指标,用于轴承的运行状态评估和剩余使用寿命预测,且效果更优。

(2)将时域和时频域特征指标作为输入,PCA方法处理所得综合指标为输出,搭建SVR预测模型并用DEGWO算法优化,优化后的SVR模型进行滚动轴承的运行状态评估及剩余使用寿命预测,其预测结果充分体现所提方法的有效性和实用性,并发现输入/输出指标的选择对模型预测性能影响较大。本文特征指标的构造和使用为轴承运行状态评估与剩余寿命预测的研究提供了参考。

(3)本文采用DEGWO、GWO和GSA算法优化SVR模型以及LSTM模型对轴承进行寿命预测,不同模型的预测结果通过预测评价指标进行对比,发现用DEGWO算法优化后的SVR模型较其他模型具有更高的预测精度,优化算法的选用对模型预测性能影响较大。进一步来说,故障诊断领域优化算法的改进和使用可作为重要研究方向和思路。