多重事件触发机制下四旋翼飞行器的姿态跟踪控制

常璧麟,龙离军,程杨,刘雪意,申子晗,王泽通

(东北大学信息科学与工程学院,110819,沈阳)

近年来,四旋翼飞行器由于其结构简单、质量小、噪声低、易于操作等优点而成为一种流行的小型飞行器,并在紧急搜救、航拍摄影、军事侦察等领域得到了广泛的应用[1-3]。

事件触发控制是一种可以高效利用资源的控制策略。在传统的周期采样控制中,系统以固定的时间间隔进行信息传输与控制更新,不可避免地会造成系统资源的浪费。在事件触发控制中,系统信息的传输则由系统内特定的事件触发,即只在系统需要时才进行信息采样与控制更新,能有效节省通信与计算资源。另外,事件触发控制还能提供更强大的反馈能力,特别是在抵御非线性、补偿不确定性方面具有较大的优势[4-5]。

由于四旋翼飞行器本身是一种很复杂的非线性系统,且在飞行过程中易受到气流扰动、陀螺效应等物理效应的影响,设计其控制系统也就变得异常复杂[6]。目前,国内外研究者在四旋翼飞行器控制系统的设计上开展了大量的研究工作。其中,常见的控制器设计方法主要有PID控制、鲁棒控制、反步控制等。文献[1]研究了基于反步法的四旋翼飞行器增稳混合控制方法,用反步法设计的控制器对飞行器姿态进行控制,用模糊自适应PID控制器对飞行器高度和位置进行控制;文献[2]研究了基于反步法的四旋翼飞行器控制系统设计问题;文献[5]采用反步法实现了四旋翼飞行器轨迹跟踪。然而,如何利用事件触发机制,在实现四旋翼飞行器的姿态跟踪控制的前提下节约系统的计算与通信资源却鲜有报道。

本文针对四旋翼飞行器系统构建了多重事件触发机制,使得飞行器的4个控制输入的欠驱动系统达到了预期的跟踪效果。与文献[5]相比,不仅达到了预期的控制效果与控制精度,又节约了系统的通信与计算资源。本文首先在滚转角数学模型的基础上运用反步法设计出控制律,然后在所设计的控制律的基础上引入事件触发控制机制,构成事件触发控制器,并由Lyapunov稳定性理论证明了所设计的控制器使系统保持稳定,且能避免Zeno现象。类似地,利用与滚转角系统相同的控制器设计方法对四旋翼的其他3个系统设计了事件触发控制器,并由这4个控制器的触发机制构成飞行器系统的多重事件触发机制。仿真结果表明,与周期采样控制器相比,所设计的多重事件触发机制构成的事件触发控制器不仅达到了与周期采样控制器相同的控制效果,又有效节省了系统的计算与通信资源。

1 四旋翼飞行器建模

1.1 动力学方程

四旋翼飞行器通过调节4个螺旋桨的转速来控制飞行过程中的姿态与位置。本文基于4个假设构建四旋翼飞行器的动力学模型:①四旋翼飞行器是刚体,在飞行过程中不发生形变;②四旋翼飞行器的结构严格对称;③四旋翼飞行器质量与转动惯量保持不变;④飞行过程中四旋翼飞行器处于相对稳定状态,滚转角φ与俯仰角θ均在20°内[7]。

ωi—第i个螺旋桨的转速。图1 机体坐标系与惯性坐标系Fig.1 Body coordinate system and inertial coordinate system

由牛顿定律可得飞行器在惯性坐标系下的线加速度方程为[8]

(1)

由于四旋翼飞行器结构严格对称,因此定义机体转动惯量I=diag(IxIyIz)。在假设条件下可得角运动方程[9]

(2)

其中,kd为转动系数,L为四旋翼飞行器的电机到飞行器重心的距离。

1.2 状态空间模型

为化简状态变量,定义函数

(3)

考虑到U1=Fs,得到状态空间表达式

(4)

式中b1、b2、b3均不为0。

2 反步控制器的设计

反步法是针对非线性系统的一种系统化的、递归的控制器设计方法[10-12]。反步法基本思想是将复杂的非线性系统根据其内部联系分解为若干个子系统,从第一阶子系统开始,设计该阶系统的Lyapunov函数,在保证第一阶子系统具有稳定性的基础上获得该子系统的虚拟控制律。完成第一阶系统的设计后,在第二阶系统中以第一阶系统的虚拟控制律作为第二阶系统的跟踪函数,以类似于第一阶系统的设计方法设计出第二阶子系统的虚拟控制律。依此类推,进而得到整个闭环系统的虚拟控制律[13]。

以滚转角系统为例,假设滚转角跟踪给定的参考信号为x10,用反步法设计该系统的控制律。令

x1=φ;x2=φ;u(t)=U2

(5)

则滚转角系统可表示为

(6)

定义滚转角误差为

z1=x1-x10

(7)

针对z1,构造正定函数

(8)

对V1进行求导,有

(9)

设计控制律α1

(10)

式中c1>0。

针对α1,定义误差

z2=x2-α1

(11)

引入Lyapunov函数

(12)

对V2进行求导,得

(13)

对z2求导,得

(14)

考虑到

x2=z2+α1

(15)

联立式(10)(13)(14)(15),得

(16)

(17)

式中c2>0。

综合式(5)(7)(10)(11)(17),滚转角φ系统的控制律为

(18)

同理,也可以得到U1、U3、U4的控制律。

z方向系统的控制律为

(19)

x方向系统的控制律为

(20)

式中p1=cφsθcψ+sφsψ。

y方向系统的控制律为

(21)

式中p2=cφsθsψ-sφcψ。

俯仰角θ系统的控制律为

(22)

偏航角ψ系统的控制律为

(23)

3 多重事件触发机制

随着网络控制系统的发展,事件触发控制以其有效节约网络系统的计算与通信资源的优势而得到国内外研究者的广泛关注[14-15]。在传统的周期采样控制中,系统以固定频率采样与执行操作[16-17]。这种控制策略缺乏一定的智能性,可能会造成一系列不必要的操作以及资源的浪费[18]。由事件触发机制所设计的控制器只有在系统的特定事件被触发时才会采样或执行操作,即只有在系统需要时才会进行信息传输和控制更新[19-20]。

本节提出了一种事件触发机制,在第2节构建的反步控制器的基础上,首先为滚转角系统设计了事件触发控制器。所设计的控制器由Lyapunov稳定性理论证明可以使系统保持稳定,且可以避免Zeno现象。然后,分别对四旋翼飞行器其余3个状态变量的系统设计了事件触发控制器,其中每个控制器都对应其自身的触发机制。所设计的4个控制器可以在四旋翼飞行器上同时工作,并由这4个控制器的触发机制构成的多重事件触发机制提供触发时刻。

3.1 事件触发机制

以滚转角系统式(6)为例,设计事件触发控制器

u(t)=w1(tφ,k),∀t∈[tφ,k,tφ,k+1)

(24)

(25)

式中:ε1为一正常数,k∈N+;{tφ,k}是滚转角的触发时刻序列,由事件触发机制生成

(26)

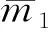
以Lyapunov稳定性理论来证明所设计的事件触发控制器使系统保持稳定。

(27)

式中σ和Δ是给定的正常数,即系统式(6)的所有状态变量都是有界的。

证明对V求导,得到

(28)

(29)

在事件触发机制式(26)中,由事件触发条件可以得到|w1(t)-u(t)|≤m1,∀t∈[tφ,k,tφ,k+1)。设λ(t)为一连续的时变参数,且满足λ(tφ,k)=0,λ(tφ,k+1)=±1,|λ(t)≤1|,∀t∈[tφ,k,tφ,k+1),则有

w1(t)=u(t)+λ(t)m1

(30)

由式(30),并结合式(17)(25)得到

z2b1m1λ(t)

(31)

注意到反正切函数arctan具有性质

(32)

式中:κ∈R;ε是一常数,且满足ε>0。

联立式(31)(32)并化简,得到

(33)

(34)

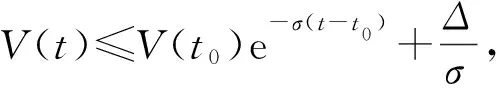
通过定理1证明所设计的事件触发控制器确保系统不会出现Zeno现象。

定理1考虑系统式(6),事件触发控制器式(24)可以确保系统不会出现Zeno现象,即存在t*>0,使得系统的执行时间间隔组成的集合{tφ,k+1-tφ,k},∀k∈N+的下界是t*。

证明设

e(t)=w1(t)-u(t),∀t∈[tφ,k,tφ,k+1)

(35)

对|e(t)|求导,有

(36)

由式(25)可得

(37)

根据引理1知,z2、α2、f1(X)及其导数是光滑有界的函数,令

(38)

≤ζ(tφ,k+1-tφ,k)

(39)

又因为

(40)

所以

(41)

3.2 四旋翼飞行器的多重事件触发机制

按照3.1节中滚转角系统事件触发控制器的设计方法,设计其余状态变量系统的事件触发控制器,结果如下。

垂直位移z方向系统为

(42)

俯仰角θ系统为

(43)

偏航角ψ系统为

(44)

设计的四个事件触发控制器在四旋翼飞行器上同时工作时,可构成多重事件触发机制,以此提供触发时刻。

4 仿 真

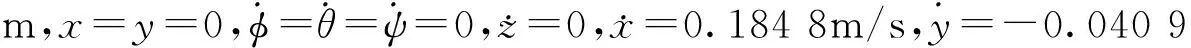
图2与图3分别为多重事件触发机制下与周期采样控制下φ、θ、ψ、z的跟踪效果。对比两图可以看出,多重事件触发机制下4个状态变量的跟踪效果达到了与周期采样控制下相接近的效果,二者都能很好地跟踪给定的参考信号。

图2 多重事件触发机制下φ、θ、ψ、z的跟踪效果Fig.2 Trajectories of states φ, θ, ψ and z under multi-event triggered mechanism

图3 周期采样控制下φ、θ、ψ、z的跟踪效果Fig.3 Trajectories of states φ, θ, ψ and z under periodic sampling control

图4为在多重事件触发机制下系统输出的信号与给定参考信号的误差。可以看出,在事件触发控制的整个过程中,系统误差都保持较低值,跟踪效果良好。

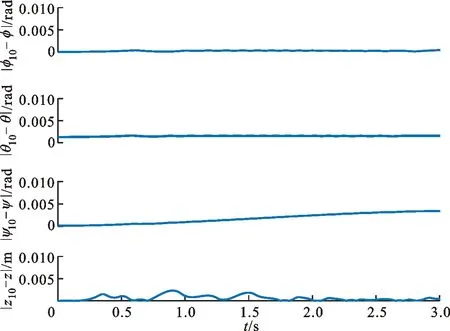
图4 多重事件触发机制下的跟踪误差Fig.4 Tracking errors under multi-event triggered mechanism

图5为多重事件触发机制下触发时刻及触发间隔的仿真结果。可以看出,在此次仿真中,系统一共触发150次,任意两次触发时刻之间间隔最小为0.021 s>0,表明系统不会发生Zeno现象。

图5 多重事件触发机制下的触发间隔Fig.5 Inter-event time under multi-event triggered mechanism

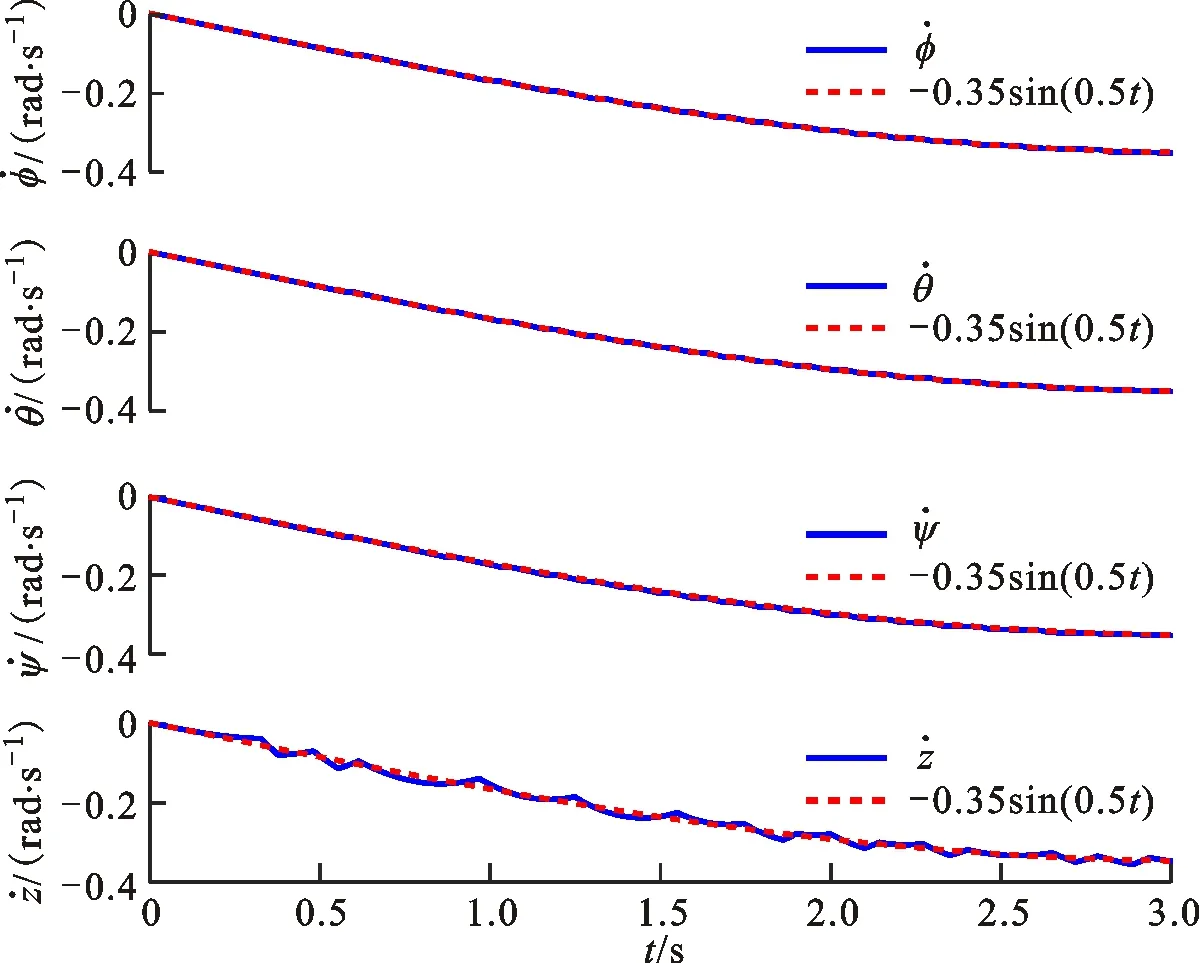
图6 多重事件触发机制下的变化Fig.6 State trajectories of under multi-event triggered mechanism

图7 多重事件触发机制下的变化Fig.7 Trajectories of states x, under the multi-event triggered mechanism

在四旋翼4个状态的系统中分别添加干扰信号d1、d2、d3、d4

(45)

四旋翼系统的状态空间表达式变为

(46)

在有干扰条件下进行仿真实验,结果如图8与图9所示。分析可知,若给四旋翼4个状态的系统增加一定的干扰项,所设计的事件触发控制器依然可以使四旋翼的4个状态变量跟踪给定的参考信号。

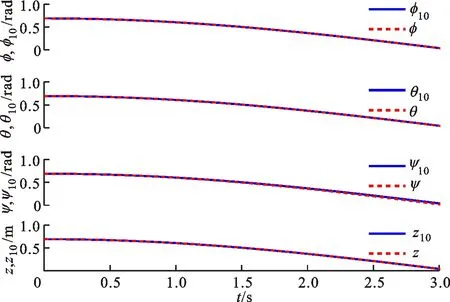
图8 干扰情况下φ、θ、ψ、z的跟踪参考信号Fig.8 Trajectories of states φ, θ, ψ and z in the case of interference

图9 干扰情况下φ、θ、ψ、z的跟踪误差Fig.9 Tracking errors of states φ, θ, ψ and z in the case of interference

根据本小节仿真结果可知,本文设计的多重事件触发机制仅需150次触发就可以让φ、θ、ψ、z这4个状态变量跟踪所给定的参考信号,而在周期采样控制中,飞行器需要连续通信3 000次才能达到同样的控制效果。并且,本文设计的事件触发控制器也能较好地抑制扰动。综合可知,本文设计的多重事件触发机制可以有效降低系统的通信与计算资源的损耗,比传统的周期采样控制更具优势。

5 结 论

本文针对四旋翼飞行器的姿态跟踪控制问题提出了一种多重事件触发机制,为四旋翼飞行器4个状态变量的系统构建了事件触发控制器,并利用Lyapunov稳定性理论证明了所设计的控制器可以使系统保持稳定。与以往的周期控制器相比,在保证跟踪效果的同时又节省了系统的计算与通信资源。本文结论如下。

(1)在多重事件触发机制下,所设计的事件触发控制器仅需触发150次就可以达到周期采样控制器连续采样3 000次的跟踪效果,可以有效地降低系统的计算与通信资源。

(2)在一定的扰动下,本文设计的事件触发控制器能使所控制的4个状态变量稳定地跟踪给定的参考信号,且保持较低的跟踪误差，说明本文设计的事件触发控制器具有一定的抗干扰能力。

(3)本文设计的控制器在使用时需满足飞行器的滚转角与俯仰角均在20°以内的条件。

后续的工作可综合考虑飞行器在自然环境中受到的干扰,设计具有抵抗复杂干扰能力的事件触发控制器。