计及风电消纳下基于纳什议价理论的多综合能源系统协同运行

帅轩越,王秀丽,王志成,郭慧,马志程

(1.西安交通大学电气工程学院,710049,西安;2.国网甘肃省电力公司电力科学研究院,730070,兰州)

能源是人类赖以生存的物质基础,同时人类社会的发展也离不开能源的供给[1]。随着煤炭、石油、天然气等不可再生能源的大规模开发,人类社会面临着能源日益枯竭与环境恶化的危机[2-3]。

为提高对能源的利用率,第三次工业革命中提出了能源互联网,并引发了全球的高度关注[4]。综合能源系统作为能源互联网的物理载体,能够对能源的产生、输送、转换、分配等环节进行协调与优化[5-7]。相比于传统相互独立运行的电、气、热系统,综合能源系统能实现各类能源之间的灵活转换,旨在提高系统能源利用率[8]。

目前,已有诸多学者针对综合能源系统的运行优化展开研究。文献[9]从系统运行经济性出发,综合考虑了电、热、冷、气共4种能源类型的转换,建立园区综合能源系统经济优化调度模型,突出多能互补、阶梯利用能够显著降低系统运行经济成本,为综合能源系统的优化调度奠定了基础框架。随着低碳理念的不断深入,碳排放引起广泛学者的关注。文献[10]在传统综合能源系统的研究上引入光热电站,并结合低碳背景在系统运行成本中考虑碳排放成本,建立考虑多能转换与光热电站参与的综合能源系统低碳经济运行模型。然而,文献[9-10]均从源侧的角度展开研究,负荷侧的需求响应也能参与系统的优化调度,从而实现源-荷协同优化。文献[11]计及了电、热、气综合需求响应,所建立的模型在削峰填谷、减少弃风弃光以及降低系统运行成本上更具优势。

然而,这些研究均属于单目标优化的范畴。事实上,综合能源系统的优化指标不唯一,如系统运行成本最低、可再生能源消纳率最大、碳排放最少等,调度人员需要对不同指标权衡考虑。目前,针对多目标优化问题主要有两大思路:一是将多目标问题转换为单目标问题[12-14],通过设置不同指标的权重系数将目标统一化,所得最优方案具有唯一性;二是求解Pareto最优解集[15-16],即给出优化问题的多个非劣解供参考。对于前者:文献[12]以系统运行成本最小与系统污染气体排放量最小为目标,建立了综合能源系统经济环境调度模型,利用线性加权的方法将多目标问题转换为单目标问题,保证了不同目标能够无量纲求和。但是,这种评价方法较为简单,不能很好地统一不同指标的灵敏度。文献[13]结合了模糊规划理论的优点,通过建立隶属度函数将不同目标归一化、模糊化,使得不同指标的量纲保持一致,同时统一了不同指标的灵敏度。然而,文献[12-13]在权重系数上选择具有一定主观性。文献[14]所使用的改进熵权法能够从数据本身出发,通过熵的含义计算每个目标的熵权,从而得到客观的权重系数。对于后者,文献[15-16]直接对多目标优化问题进行求解,分别使用改进型多目标粒子群优化算法与带精英策略的非支配排序遗传算法求解得到Pareto最优解集。

但是,这些研究均针对单个综合能源系统展开研究,随着物理互联与信息交互技术的发展,多个综合能源系统也能进行能量交互。此类问题的关键在于如何对多个参与者的利益进行分配,而博弈论为交互决策问题提供了参考。博弈论主要分为非合作博弈[17]与合作博弈[18]。文献[17]针对多个园区购电过程中的竞争问题,基于非合作博弈论建立了多园区综合能源系统的博弈优化模型,所提模型能较好地权衡多园区间的利益。文献[18]建立了多个综合能源微网间的合作博弈模型,并利用Shapley值法与功率交互贡献度法对各微网的收益进行分配,维持了多微网协同运行的积极性。非合作博弈侧重分析多个参与者间的竞争现象,重点关注纳什均衡点。与非合作博弈不同的是,合作博弈注重整体利益最大与利益分配问题,本文重点关注合作博弈问题。

需要指出的是,大多研究仅针对单个综合能源系统的多目标优化问题展开研究,鲜有研究关注于多目标背景下多个综合能源系统的优化问题。如何建立一套合理的运行机制权衡不同综合能源系统的利益,同时兼顾系统调度人员对不同目标的偏好需求,是值得思考的问题。

因此,本文以电-热综合能源系统(HE-IES)的运行成本与风电消纳率作为研究指标,建立多个HE-IES的多目标合作博弈模型。利用多目标加权规划法将多目标问题转换为单目标优化问题,进一步采用纳什议价的方法对所有HE-IES的合作效益进行分配,通过算例分析验证了所提模型的有效性与合理性。

1 多电-热综合能源系统运行框架

假定所研究的场景由多个HE-IES与配网构成,且多个HE-IES由调度中心统一调度。HE-IES内主要包括热电联产(CHP)单元、热泵(HP)、储能电池(ES)、储热罐(HS)、风机(WT)等设备,多个HE-IES框架与HE-IES内部能流关系如图1所示。

由图1可知:一方面,HE-IES主要通过燃气轮机与热泵进行产能,储能电池与储热罐负责协调配合;另一方面,HE-IES也能通过气网与电网相连进行能源交易,实现内部供需平衡。由于配电网侧的售电价高于购电价,HE-IES独立运行时与配电网进行电能交易将产生交易亏损。但是,当多个HE-IES通过联络线互联时,HE-IES也能与其他HE-IES进行电能交互,从而减少与主网进行电能交易过程中的价格套利现象。

2 电-热综合能源系统数学模型

设所研究的场景包含HE-IES的总数为n,研究周期为T。

2.1 热电联产单元

CHP主要由燃气轮机组成。HE-IES通过外购天然气供燃气轮机[19]燃烧,燃气轮机同时产生电能与热能。CHP单元燃气成本表示为

(1)

约束条件表示为

(2)

(3)

(4)

2.2 热泵

热泵[20]能将电能转换为热能,约束条件为

(5)

(6)

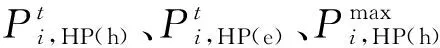
2.3 储能电池

储能电池能实现电能的时空转移。本文以蓄电池作为储能电池。储能电池调度成本为

(7)

约束条件为

(8)

(9)

(10)

(11)

(12)

2.4 储热罐

与储能电池类似,储热罐同样能实现热能的时空转移。储热罐调度成本为

(13)

约束条件为

(14)

(15)

(16)

(17)

(18)

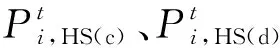
2.5 与配电网电力交易

假定配电网侧电价采用分时电价,HE-IES能在电能不足时从配电网购电,在电能盈余时向配电网售电,则相应交易成本与约束条件可表示为

(19)

(20)

2.6 切负荷

当HE-IES内部能源供给小于需求时,为了维护系统的安全性,HE-IES将采取切负荷的手段以保证有功出力与负荷间的平衡。本文简化处理,认为负荷切除仅为电负荷,HE-IESi的切负荷成本为

(21)

约束条件为

(22)

3 多电-热综合能源系统多目标优化 运行模型

3.1 多电热综合能源系统运行分析

当多个HE-IES间签订合作协议,通过联络线互联进行功率交互,HE-IESi的相关约束为

(23)

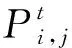
在多HE-IES互联的基础上,每个HE-IES内电、热有功出力与负荷需满足平衡约束,则第i个HE-IES的电、热有功平衡约束表示为

(24)

(25)

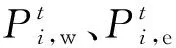
当HE-IESi处于独立运行模式时,式(23)变为

(26)

3.2 多目标问题的转换

本文所考虑的目标函数有系统运行经济成本与系统风电消纳率两个指标,具体表示为

(27)

(28)

为权衡两个指标的评价标准,设单位弃风成本为λw,将目标函数归一为成本,进一步采用多目标加权规划的方法构建目标函数。所转换的单目标优化问题可表示为

(29)

式中:λ1与λ2分别表示两个指标的权重系数,指标的系数越大,说明该指标的重要程度越高;Fi为HE-IESi经加权处理后的综合运行成本。

4 基于纳什议价理论的分配方法

为维持参与合作中HE-IES的积极性,需要合理地对各HE-IES的收益进行结算。考虑到纳什议价模型能满足所有参与合作个体的帕累托最优,本文采用纳什议价模型进行求解。该模型的表达式为

(30)

值得注意的是,当参与者数量多于2时,式(30)为非凸问题,求解难度较大。采用文献[21-22]中的方法进行数学转换,具体推导过程见本文首页OSID码中的开放科学数据与内容附录A。经转换后,两个凸的子问题分别为

(31)

(32)

由式(32)可求得所有HE-IES经过纳什议价后的综合运行成本,再利用式(29)中的权重系数进一步分配,得到每个HE-IES的运行成本与弃风成本,分别表示为

(33)

(34)

5 算例分析

5.1 算例描述

为了进一步验证所提方法的有效性,选取3个HE-IES作为算例进行分析,利用MATLAB Yalmip工具进行建模,结合Ipopt求解器求解。设一天研究时段T=24 h,与配电网间的功率交互上限均为50 kW,切负荷上限与单位切负荷成本分别为200 kW与0.8 元/kW,单位弃风成本为0.5 元/kW,HE-IES1与HE-IES2、HE-IES1与HE-IES3、HE-IES2与HE-IES3的功率交互允许上限分别为50、40、30 kW,各HE-IES内储能电池、储热罐的初始容量均为额定容量的一半。各HE-IES内的风电出力、电热负荷以及净电负荷如图2所示,电网分时电价见表1,HE-IES内CHP、GB、ES以及HS等设备参数参考文献[23],详细见本文首页OSID码中的开放科学数据与内容附录B。

(a)风电出力

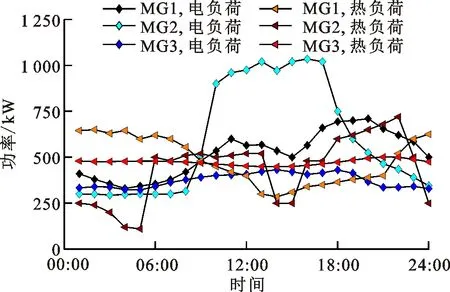
(b)电热负荷

(c)净电负荷图2 各HE-IES内风电出力、电热负荷以及净电负荷Fig.2 Wind power output,electric heating load and net electric load in each HE-IES

表1 电网分时电价

5.2 算例流程

算例的求解具体流程如下。

(1)初始化所有HE-IES的基础数据,包含一天内风电预测出力、电热负荷、设备参数以及各联络线交互极限等。

(2)设定系统运行经济成本与系统风电消纳率两个指标的权重系数,将多目标优化问题转换为单目标问题。

(3)利用CPLEX求解器分别计算各HE-IES独立运行(仅与配电网互联,各HE-IES不互联)与协同运行(各HE-IES互联)下的运行成本。

(4)利用IPOPT求解器求解各HE-IES的议价模型,即式(32),得到各HE-IES的议价转移,进而得到合作博弈后各HE-IES需承担的综合运行成本。

(5)根据步骤(2)中所设定的权重系数,将各HE-IES的综合运行成本按式(33)(34)进行分配计算,得到各HE-IES需承担的运行成本与弃风成本。

5.3 结果分析

记3个HE-IES独立运行为模式1,3个HE-IES协同运行为模式2。

为探究关于两个指标的单目标优化下3个HE-IES间功率交互的合理性,依次取总运行成本最低(λ1=1,λ2=0)和总弃风成本最低(λ1=0,λ2=1),模式2下3个HE-IES间的功率交互见图3。

(a)总运行成本最低

(b)总弃风成本最低图3 单目标优化下3个HE-IES间的功率交互曲线Fig.3 Power interaction curve between three HE-IESs under single objective optimization

结合图2与图3a可知:当所有HE-IES处于协同运行时,一天中00:00～05:00时段HE-IES1与HE-IES3均向HE-IES2输送电功率,这是因为HE-IES2处于缺电状态,同时HE-IES1与HE-IES3处于余电状态,HE-IES群内通过功率交互减少与主网的电力交易以达到减少系统总运行成本最低。同样地,对于图3b,一天中00:00～05:00的功率传输趋势总体表现为HE-IES2内的电功率向HE-IES1与HE-IES3传输。这是因为HE-IES2内净电负荷在00:00～05:00时段较高,会产生大量弃风现象,为有效减少弃风成本,HE-IES2需将自身电功率传输至其余HE-IES。需要指出的是,虽然HE-IES1与HE-IES3中的风电出力在00:00～05:00时段较高,但二者的电负荷水平在00:00～05:00时段也很高,因此大量风电资源被就地消纳,弃风程度低于HE-IES2。其余时段的分析与00:00～05:00时段类似,不再赘述。

为对比多目标问题下HE-IES协同运行下的优越性,以λ1=0.6、λ2=0.4为例进行比较。两种模式下3个HE-IES的运行成本与储能设备容量总和分别见表2与表3。

表2 两种模式下各HE-IES的运行成本

表3 两种模式下各HE-IES的弃风成本

由表2与表3可知:相比于模式1,所有HE-IES运行于模式2时的总运行成本与总弃风成本均得到减少,分别减少了660.14、222.03元。每个HE-IES经过纳什议价后各自的运行成本与弃风成本均有所减少,且每个HE-IES的运行成本均减少了220.05元,弃风成本均减少了74.07元,实现了所有HE-IES的帕累托最优。

两种模式下3个HE-IES内的设备优化出力分别见图4与图5(图中CHP(e)表示CHP的电出力),协同运行模式下3个HE-IES的功率交互曲线见图6。

(a)HE-IES1

(b)HE-IES2

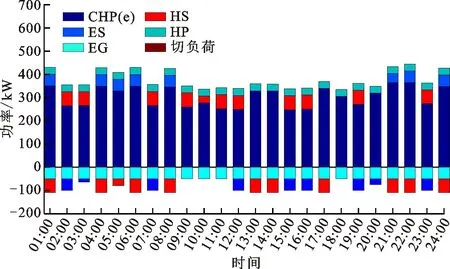
(c)HE-IES3图4 模式1下一天中各HE-IES内的设备出力以及与 配电网的电力交易Fig.4 Output of each HE-IES equipment and electricity transaction with the distribution network in a day under mode1

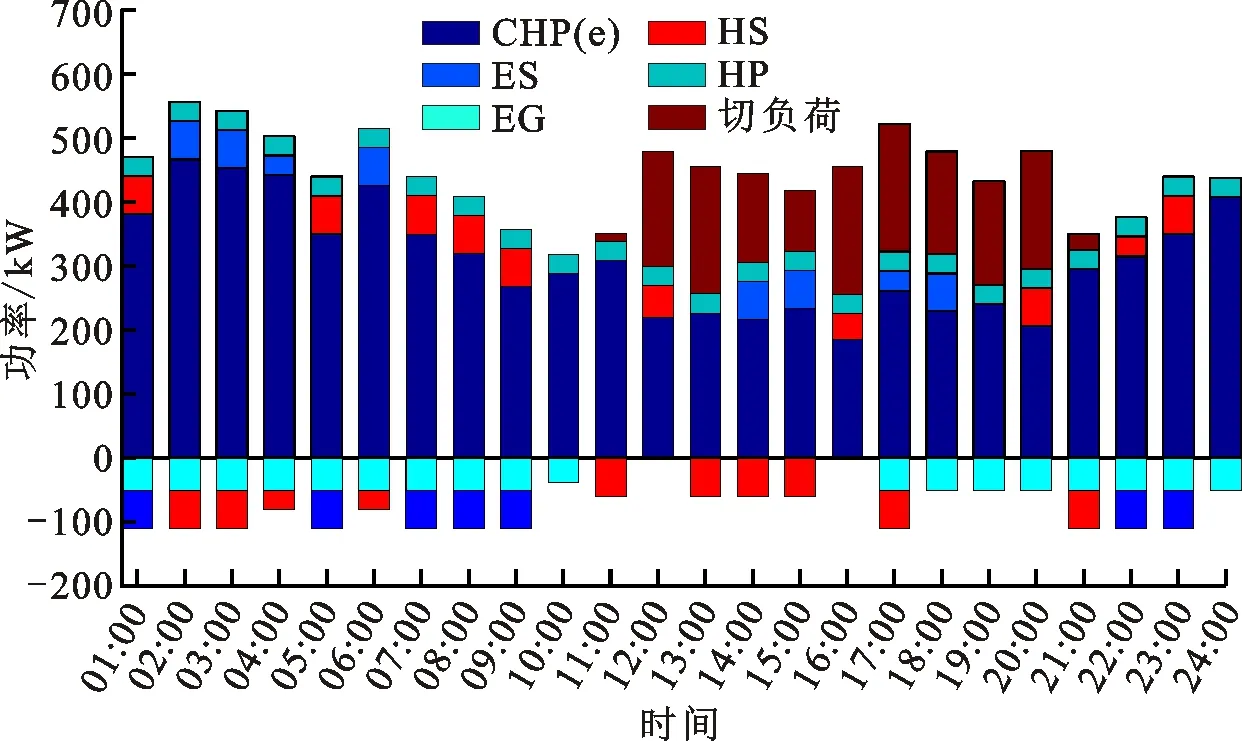
(a)HE-IES1

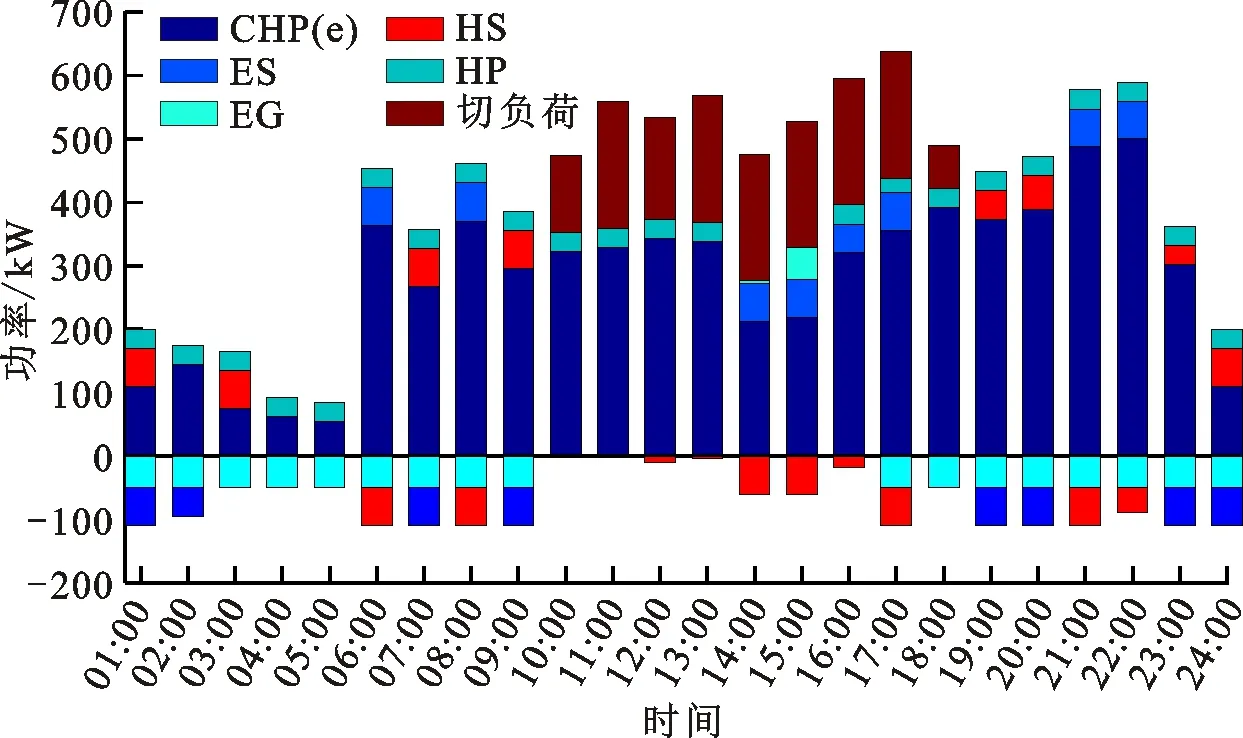
(b)HE-IES2

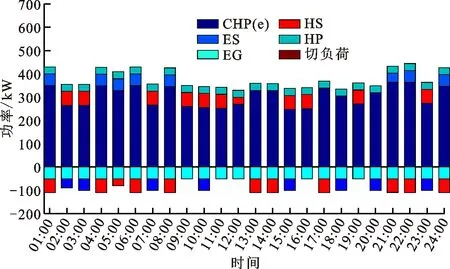
(c)HE-IES3图5 模式2下一天中各HE-IES内的设备出力以及与 配电网的电力交易Fig.5 Output of each HE-IES equipment and electricity transaction with the distribution network in a day under mode2

图6 协同运行模式下3个HE-IES的功率交互曲线Fig.6 Power interaction curve of three HE-IESs in cooperative operation mode

由于设定的权重系数λ1与λ2分别为0.6、0.4,即调度人员认为系统运行成本与弃风成本的重要性分别为60%与40%,因此在优化过程中需综合考虑两个指标的重要程度。结合图4与图6进行分析可知:对于提高可再生能源消纳率这一指标,仅需减少系统弃风成本,因此3个HE-IES间的功率交互有40%的贡献用于减少一天内系统弃风成本总和;对于减少系统运行成本这一指标,需综合考虑3个HE-IES内的CHP发电成本、电储能调度成本、切负荷成本以及与配电网电能交易成本,因此3个HE-IES间的功率交互有60%的贡献用于减少一天内系统运行成本总和。以HE-IES1为例,模式1与模式2下切负荷主要发生于11:00～21:00时段,相比于模式1,模式2下18:00～21:00时段的切负荷得到减少,结合图6可知,这是因为18:00～21:00时段HE-IES2向HE-IES1传送电功率,以减少HE-IES1在该时段的负荷切除,同时兼顾改善系统的风电消纳。同时,HE-IES1的电储能与热储能的出力在一天内17:00～24:00时段变化较为明显,这是因为模式2下引入了HE-IES间的功率交互,使得每个HE-IES内的设备出力能够在一定程度上灵活调整,进一步减少系统运行成本。

依次取λ1为0、0.1、…、1,所提模型在模式2下3个HE-IES的总运行成本与总弃风成本如图7所示,3个HE-IES的功率交互曲线见本文首页OSID码中的开放科学数据与内容附录C。

图7 不同加权系数下3个HE-IES的总运行成本与 总弃风成本Fig.7 Total operating costs and total wind curtailment costs of three HE-IESs under different weighting factors

由图7可知:随着λ1逐渐增加,HE-IES的总运行成本逐渐减少,同时HE-IES的总弃风成本逐渐增加。这是因为λ1的增加使系统运行成本的权重增加,即系统运行成本最小的重要程度增加,同时λ2逐渐减少,使得风电消纳的重要程度降低。另外,当λ1分别在0～0.1与0.9～1区间内,HE-IES的总运行成本减少的程度较为剧烈。这是因为在该区间内λ1与λ2差距较大,导致系统的总运行成本与总弃风成本的灵敏度较高。

6 结 论

本文考虑了HE-IES经济运行成本与风电消纳率两个指标,在多HE-IES联合运行的背景下提出了基于纳什议价理论的多HE-IES协同运行多目标优化模型,主要结论如下。

(1)相比所有HE-IES独立运行,所提模型能有效减少所有HE-IES的总运行成本,同时提高HE-IES群总体风电消纳水平,其中总运行成本减少了660.14元,总弃风成本减少了222.03元。

(2)利用纳什议价的方法对所有HE-IES的运行成本与弃风成本进行分配,每个HE-IES的运行成本均减少了220.05元,弃风成本均减少了74.07元,满足所有HE-IES的帕累托最优,所有HE-IES的运行成本与风电消纳均得到改善。

(3)所提模型能通过调整两个指标的权重系数灵活适用各类场景,较好地权衡了两个指标的重要程度,应可为系统调度人员提供参考方案。