自适应Harris角点提取的点云粗配准算法

近年来,随着激光雷达技术的日趋成熟和成本降低,三维点云配准技术在三维重建、场景语义分割、无人驾驶等领域发挥着无可替代的作用

。目前,采用的点云配准技术一般分成粗配准和精细配准两部分。粗配准的核心目的是为了提取点云的特征信息,然后计算特征的相似度,以相似度信息配准点云。特征提取在处理大型三维点云数据时可以起到降采样的作用,减小点云平移和旋转等误差,从而提升配准效率。点云特征提取主要分为局部特征提取、全局特征提取和基于深度学习的点云特征提取共3类。

点云的局部特征使用点云空间分布特征或者几何结构特性来量化计算。在几何特征提取算法中,快速点特征直方图算法

以点云数据关键点的快速特征直方图相似性对点云进行初始匹配,然后使用采样一致性初始配准算法求得初始转换矩阵,最后使用迭代最近点(ICP)算法

精确匹配得到点云变换矩阵。Li等保留了点特征直方图(SPFH)中对点描述的主要几何特性,并分别计算查询点的邻域中每一个点的简化点特征直方图,再将SPFH加权形成最后的快速点特征直方图,从而降低了算法复杂度

。Mellado等提出Super-4PCS,通过角度约束减少四点法(4PCS)

在寻找匹配对时产生的无效对,从而减少点云中产生的候选对数目

。同时,栅格化点云数据,降低计算距离的二次复杂度。当点云几何结构没有明显特征或者局部相似度较高时,局部特征提取算法不能很好地识别并加以区分。面对包含大量噪声的实际数据,点云局部特征可信度较低。

点云全局特征提取主要是针对点云整体进行旋转、平移等空间变换,通过统计概率密度、抽取特征值和特征向量等操作来获得鲁棒的特征信息。受图像处理的启发,最初的全局特征信息提取往往基于二维视角的方法将三维点云数据视为若干二维图像的集合。视点特征直方图摆脱二维图像算法,通过对所有点的坐标求均值找出质心,计算视点和此质心之间的向量,并将其归一化处理

。对所有点计算此向量与其法线之间的角度,并将结果归并为直方图。

随着卷积神经网络在各个领域的卓越表现,针对三维点云数据的研究也逐渐从低层次几何特征提取向高层次语义理解过渡。深度神经网络可以通过学习能力来解决点云数据的无序性问题。PointNet和DeepSet网络首次提出这类问题的研究方法,采用对称函数处理初始点云,从而优化了点云的无序性

。动态图卷积神经网络提出了一个基于图卷积神经网络的EdgeConv层来获取局部特征,在保证置换不变性的同时捕获局部几何信息,解决了PointNet没有处理局部特征的问题

,但该网络计算量较大。多视角卷积神经网络(MVCNN)将点云中采样到的80个视图投影到二维空间,然后由二维的卷积神经网络处理

。SO-Net网络结构使用自组织映射进行分层特征提取

。3DFeat-Net使用弱监督学习来学习点云的描述子

。处理点云数据大多采用多层感知机来提取每个点的语义特征,但是这类方法没有很好地学习点的局部特征,并且鲁棒性不好。在点云分类分割中,引入多尺度特征提取的方法能够同时考虑输入点云的全局特征和局部特征。MSP-Net使用多尺度特征对点云进行分类,该方法证明了多尺度具有更好的特征提取能力,且相较于单尺度分类精度更高

。

本文提出了一种完整高效的自适应角点特征描述、提取和匹配的点云粗配准算法。图1给出了本文提出的粗配准算法流程。将传统降采样替换为改进后的3D-Harris

角点检测,引入正交梯度算子改进Harris算子;利用点云曲率约束实现角点的自适应筛选与提取,提高角点提取效率;通过改进内部形态描述子(ISS)

特征点检测算法,构建了角点几何结构的特征描述子,完成特征提取。结合阈值检测和描述子匹配,将角点匹配对进行扩展,从而完成源点云和目标点云之间粗配准。该算法是一种完善的初始点云配准算法,同时还解决了传统3D-Harris算法计算复杂度高、需要人工手动设定角点响应阈值、对噪声不鲁棒的问题,提高了配准精度,减少了配准时间。

1 相关工作

1.1 Harris角点检测算法研究现状

角点是点云中稳定的稀疏几何特征,包含了重要的结构信息。Harris算法利用卷积窗口滑动的思想来判断图像角点。图2是Harris角点检测示意,当滑动窗口在所有方向移动时,窗口内灰度值出现较大变化的像素就可能是角点。

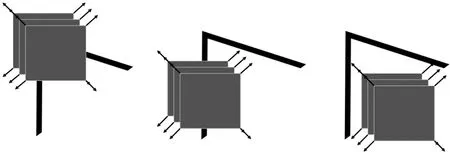
针对传统Harris算法的改进主要分为以下3方面。一是基于角点响应阈值的自适应改进方法。针对角点响应阈值需要人为多次调整的弊端,Jasani等提出用于处理阈值设定的非最大抑制方法

。胡晓彤等在此基础上结合点到弦距离累加算法(CPDA)提出自适应阈值的角点筛选方法

。但是,该方法检测出的重复角点数量较多,存在一部分误检点。在筛选圆角点时步长单一固定,不能检测多尺度下的伪角点。无重叠子区域分割法将独立阈值与每个单独点云子区域匹配,根据区域对比度自适应阈值

。该方法能够一定程度上减少手动设定阈值的时间,但是区域分割尺度需要根据点云分辨率手动设计。

二是基于Harris算子的改进方法。Sobel-Harris检测算法利用Sobel边缘检测进行角点预筛选,能够在一定程度上提高检测效率,减少漏检点与伪角点的数量,但检测结果包含角点簇

。基于曲率尺度空间的自适应角点检测子在检测过程中使用单一固定描述尺度σ,但对于复杂的图像或三维点云数据,

非常难以确定

。

三是基于角点提取、筛选的改进方法。文献[22]提出了基于灰度差分与模板的Harris角点检测算法,该算法加入灰度差分统计对对角点进行预筛选,从而提高了角点检测速率。

1.2 2D-Harris角点检测

2D-Harris算法

主要应用于数字图像处理中的角点提取。算法主要步骤描述如下。

假设图像上一点(

,

)处的灰度值为

(

,

),当该点平移(

,

)个单位后,该点处的灰度值变为

(

+

,

+

)。平移窗口的灰度变化

(

,

)为

(

,

)=

(1)

式中:

为高斯加权函数;点(

,

)为滑动窗口的中心。

利用二维泰勒展开公式可得

①确定系统的参考数列和比较数列。反映系统行为特征的数据序列，称为参考数列。由影响系统因素组成的数据序列，称为比较数列。

(2)

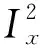
(4)利用土工织物防止分散性黏土的冲蚀破坏。工程实践证明，土工织物用于分散上坡的反滤护坡是行之有效的。通过对黑龙江省西部地区边坡治理工程运行效果进行调查发现，渠道分散性土段经土工织物反滤护砌，均收到较好的运行效果，没发生渠道塌滑破坏现象。

进一步地,将式(2)整理为

(3)

(4)

角点响应为

=det

-

(tr

)

(5)

(6)

0

04≤

≤0

06

(7)

对于边缘点,

<0;对于平坦点,

=0;对于角点,

>0。

1.3 3D-Harris角点检测

3D-Harris角点检测算法是对二维图像角点检测的拓展。具体地,以

点为原点建立一个局部坐标系:

方向是该点的法线方向,

、

方向和

垂直,在

上建立一个边长为

的小正方体检测窗口。若小正方体在点云平坦面上移动时,小正方体里的点云数量不变;若小正方体位于点云边缘上,则沿边缘滑动时,点云数量几乎不变,沿垂直边缘方向滑动时,点云数量发生改变;若小正方体位于角点上,则沿各方向滑动时,点云数量都会大幅改变。

左达一手拿着一万，一手拿着钱包，对着徐艺直摇头，“你还是太紧张了，跟我第一次下赌场一样。你得放松一点，别老想着钱包的事。”

根据Sipiran等

的思想,对小正方体内的点云进行主成分分析(PCA),并利用最小二乘法拟合出一个二次曲面。本文选择只有6项的二次曲面来表示抛物面,可以通过增加更多的项来适应更复杂的曲面。抛物面表达式为

=

(

,

)=

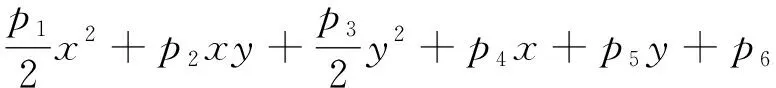
(8)

根据自相关矩阵

的计算公式,通过计算

关于

和

的偏导数来近似生成图像灰度值

。偏导数计算公式为

(9)

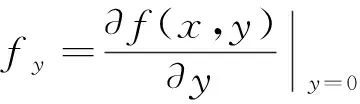
(10)

为了解决Harris最初提出的算法中导数是离散函数的问题,本文使用连续高斯函数对导数进行积分。利用曲面积分来计算自相关矩阵

中的各元素

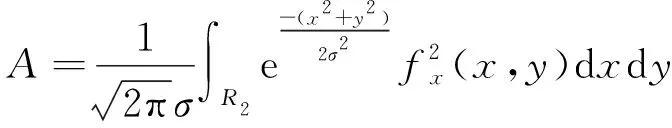
(11)

(12)

(13)

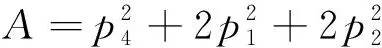
(14)

(15)

=

+2

+2

在试图解释大陆海岸线的拼图构造方面，首个学术性解释援引了“上帝之手”的说法。1668年，一位名叫弗朗索瓦·普拉特（Fran ois Placet）的法国修道士提出，《圣经》上提到的洪水摧毁了消失的亚特兰蒂斯岛，使其沉入水底，形成了大西洋。在17世纪和18世纪时，许多欧洲人认为地球是由《圣经》上提到的一系列灾难塑造成的。当时，上帝的愤怒一直是对大陆所处位置的一种流行性解释。

(16)

得到3D-Harris的自相关函数

(17)

计算3D-Harris响应值

=det

-

(tr

)

(18)

原始3D-Harris角点检测算法对三维点云数据进行了降维,导致缺失部分几何信息。而且,需要人工设置角点响应的阈值,不利于实时点云数据处理且易产生伪角点。

综上所述，网络语言的出现对汉语言文学的发展产生了一定的冲击。面对网络语言的冲击，人们应该加强对汉语言文学的学习，在日常生活和工作中重点对普通话和拼音进行推广和运用，并能够对网络语言进行合理控制，让汉语言文学经受住网络语言的冲击，并得到传承和发展。

2 自适应角点提取算法

点云模型的角点分布于模型边缘上,对于边缘点中的角点,其曲率相较于该点邻域处的平均曲率会发生突变。因此,本文在2

1小节首先对原始点云进行边缘检测,选出可能出现角点的边缘点构建待定集合

,并提出基于正交梯度的3D-Harris角点检测算法。然后,在2

2小节提出角点自适应筛选算法,在边缘点的基础上结合曲率筛选出真实角点。

2.1 基于正交梯度的3D-Harris角点检测算法

对源点云

和目标点云

进行角点特征提取后,得到源点云的角点点云

={

,…,

}和目标点云的角点点云

={

,…,

}。对于任意角点,本文用特征值和特征向量两种信息来描述该点的局部几何结构。

(19)

式中:

是激光雷达扫描模型表面生成点云数据时的平均点间距;

和

表示栅格中

方向上的最大和最小坐标。

16: break;

(20)

5:If

<

(

,

,

)

点云数据具有一定的离散性。在实际计算中为了提取出边缘点,将每个栅格单元中的点与尺寸为3×3×3的卷积模板进行卷积,用卷积操作结果作为梯度的近似值。

2:使用PCA方法估计最优包围盒;

定义

、

、

这3个方向上的卷积模板为

(

,

,

)=

(21)

(

,

,

)=

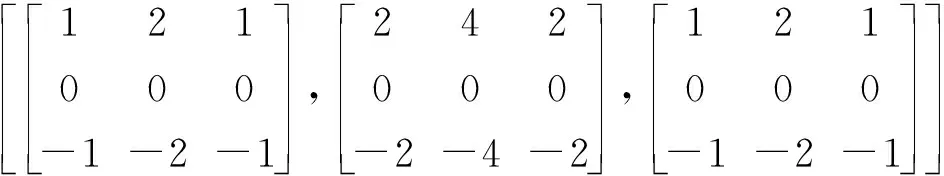
(22)

(

,

,

)=

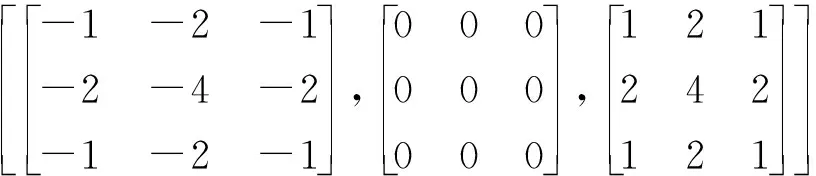
(23)

边缘梯度

(

,

,

)为

(24)

=

(

,

,

)*

(

,

,

),

=

,

,

(25)

式中*为卷积符号。

将边缘梯度幅度与预设的边缘阈值

进行比较,若

<

(

,

,

),则认为该点是边缘点

,并将该点放入边缘点集合中,

∪

。

本文将正交梯度算子引入Harris自相关矩阵,不需要通过拟合二次曲面对

轴数据进行降维,能够完整地使用三维信息,同时将自相关矩阵

拓展至三维空间中,表达式为

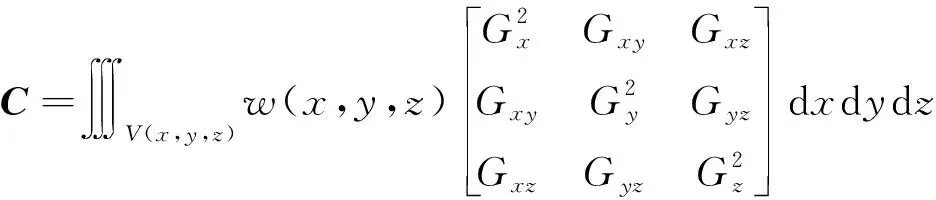
(26)

式中:

=

×

,

=

×

,

=

×

;

(

,

,

)表示该点处三重积分被积函数的积分体积;

(

,

,

)为非负加权窗函数,需满足

∭

(,,)

(

,

,

)d

d

d

=1

(27)

本文的粗配准算法包括第2节的自适应角点提取算法和本节的角点匹配与扩展。

角点响应函数

(

,

,

)为

6月下旬至7月上旬核桃当年生新梢半木质化时进行芽接，由于嫁接时间有限，对拜城县核桃实生树改接带来了制约。在核桃夏季当年生新梢5月嫩枝嫁接、6月在2年生以上枝条上采用方块芽接等嫁接技术的试验成功，不仅拉长了核桃夏季嫁接时间，而且可以有效的在2年生枝条上进行芽接，打破了传统的在当年生新梢半木质化期芽接核桃新品种的限制，为拜城县乃至南疆地区加快核桃优良品种的发展提供质量保证。

(

,

,

)=det

-

(tr

)

(28)

式中

为常系数,一般取0

04。

2.2 角点自适应筛选

传统的Harris算法需要人工设置角点响应阈值,十分耗时。阈值过大,会提取到角点簇或对非角点进行误判;阈值过小或存在噪声时,会提取到伪角点或遗漏真实角点。针对这一不足,本文提出利用曲率约束进行角点自适应筛选。点云的曲率是点云的固有几何特征,曲率作为一个描述曲面的凹凸性质的量,是采样点局部性状的体现。当曲率较大时,表明曲面的光滑程度低,会出现几何特征结构变化激烈的角点。根据微分几何性质可知,高斯曲率

是主曲率

、

的乘积,平均曲率

是主曲率之和的平均值

。

四方竹作为笋用林，由于常年挖取，对于土壤养分消耗大，导致竹林土壤肥力退化，施肥是改善这一现象的有效措施。试验结果显示，施肥能大大促进竹林的发笋，提高单位面积的竹笋产量。在施肥方案中，可以考虑以见效快的复合肥作为先导肥料保证当年生产，而以见效慢但持续性长、能改善土壤温度条件的有机肥作为长效肥保证持续生产，二者结合，作为最佳施肥方案。

定义角点候选集合

,栅格单元中的任意一个边缘点

∈

都能够用一个曲面

=

(

,

)逼近该点的邻域点云。任意一点处的曲率可用该点及其邻域点拟合的局部曲面曲率来表示。通过最小二乘法拟合一个二次曲面来表征点

的局部区域,计算点

处的主曲率

、

,平均曲率

及高斯曲率

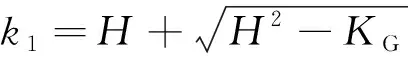
(29)

(30)

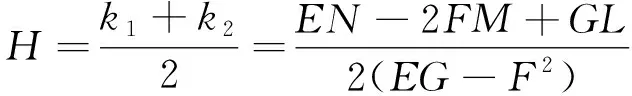
(31)

(32)

式中:

、

、

为曲面的第一基本不变量;

、

、

为曲面的第二基本不变量

。

当

≤

时,说明点

对于曲面区域

(

,

)较为平坦,不是角点;当

>

时,说明

相对于曲面的离散程度较大,可能是真实角点,将该点更新到角点候选集合中,

∪

。

利用式(28)计算

中待定角点的响应值

,并与这些点邻域曲面的曲率方差

比较。邻域曲面的曲率方差计算公式为

(33)

式中

为该曲面拟合区域内的点云数量。若

>

,则该点是角点,更新真实角点集合,

∪

;若

≤

,则该点不是角点。

自适应角点提取算法能够充分利用点云的几何信息,剔除非角点、噪声和离群点,且不用从一开始就对所有点进行角点响应计算,只需要对角点候选集合

中的待定角点计算

,大大简化了传统Harris角点提取时的计算量。同时,免去了人工设置角点响应阈值,实现了自适应角点初步筛选,简化了计算复杂度,提高了算法效率。自适应角点提取算法的伪代码如下。

输入:源点云

静态吸附动力学曲线测定：准确称取已预处理树脂5.0 g于锥形瓶中，称取0.1 g冻干粉末，用蒸馏水稀释至100 mL，520 nm下测其浓度C0。将锥形瓶置于恒温振荡器上30 ℃、100 r/min振荡，每30 min测定溶液的浓度Cj，绘制静态吸附动力学曲线。

初始化:边缘阈值

,边缘点集合

,角点候选集合

,真实角点集合

1:根据式(19)划分栅格单元;

根据建筑物沉降变形监测数据，制作累计沉降量和监测时间的曲线图，对各监测点的累计沉降量进行分析，如图2所示。

4:根据式(21)～(25)计算边缘梯度幅值

式中:

、

、

分别为

、

、

轴方向的单位矢量;

、

、

分别为点

在

、

、

轴方向上的梯度。

6:

∪

③指导交流功能：学生在自主学习过程中，不可避免会碰到一些迷惑和困难，一方面可通过课堂的讨论和答疑来解决问题，另一方面也可通过网络平台的指导交流功能来答疑解惑，这部分功能为教师和学生搭建了一个平等交流和学习的平台，学生在规定时间内通过观看微视频，参与在线答疑、讨论等环节,进行各种主题学习以及学习经验的交流，这种交流不受时间和空间的限制，不仅方便了教师与学生间的互动，而且也增加了教师与学生之间的融洽度，为进一步教学提供了方便。

7: break;

8:end if

空气质量和VOCs的任何指导可能随着时间的推移而不断变化。此外，某些化学组成与特定健康结果之间的联系可能会得到更好的理解。短期和长期的影响、寿命、暴露、累积反应和与其他化学品的相互作用，将变得明朗。这是一个复杂的领域，需要更多的工作和关注。

9:根据式(29)～(32)计算

中各点曲率

㉛Elizabeth McGrath,“Personifying Ideals”,Art History,vol.6,no.3,1983,pp.363-68.

10:For

>

11:

∪

12: 根据式(26)～(28)计算

中待定角点的响应值

;

13: 根据式(33)计算曲率方差

;

14: If

>

接触交代型铁矿床是山西第二主要类型。该类型矿石品位w(Tfe)平均41.4%，最高可达54%(如壶关县照阳沟铁矿区)，属规模相对小，但品位较高的铁矿床。因此，要想寻找“小而富”的铁矿床，应重点放在狐堰山、塔儿山及虹梯关南部一带，即主要在省内寻找既有灰岩出露又有岩体出露地区。由于碳酸盐受热液热液影响会产生围岩蚀变，即矽卡岩化，因此寻找围岩蚀变带是良好的找矿标志。在野外注意观察有无断裂构造及岩体出露情况。狐堰山地区出露岩体多为二长斑岩，塔儿山一带为二长岩及正长闪长岩类，平顺一带为闪长岩类，因岩体本身铁质含量较高，通常岩体大，所发现矿体越大。

15:

∪

2

1

2 基于正交梯度的3D-Harris角点检测算法 由于角点分布在点云模型的边缘上,要提取角点需要先对模型进行边缘检测。

17: end if

18:end for

输出:真实角点集合

3 基于自适应角点提取的粗配准算法

通常使用高斯卷积核函数做非负加权窗函数。

本节首先在第2节提取出角点的基础上,构建角点描述子,通过改进传统ISS特征检测算法中计算特征值、特征向量的步骤,完成角点描述子定义,表征角点几何结构的特征信息。然后,给出3个基于阈值的度量指标,并结合角点的特征描述子完成角点匹配与扩展,从而实现点云粗配准。

3.1 角点描述子构建

2

1

1 原始点云预处理 对于不同局部密度的非结构化点云,直接提取角点非常困难。因此,本文首先对原始点云进行预处理,生成可容纳三维点云数据的栅格单元。根据原始数据中点云的分布密度,将点云划分为多个

×

×

的栅格单元。然后,使用PCA方法估计出每个栅格单元的最优包围盒。栅格单元的空间分辨率定义为

对角点

∈{

,…,

}定义搜索半径

。角点

在半径为

的范围内存在

个支持点

∈{

,…,

}。每个支持点到

的欧式距离为

,且有‖

-

‖≤

,

<

<…<

,‖·‖表示两点间的欧氏距离。支持点构成的范围称为支持区域,计算其权值得到

(34)

计算每个支持点

对于角点

的协方差矩阵

(35)

用奇异值分解每个支持点

对于角点

的协方差矩阵cov(

),得到3个特征向量

1

、

2

、

3

和对应的3个特征值

1

、

2

、

3

,并按从大到小的顺序排列,即

1

>

2

>

3

。

通常情况下,支持区域位于平坦的区域内,

1

、

2

对内部点的分布以及噪声敏感,而

1

、

2

、

3

、

3

对内部点的分布以及噪声不敏感,且

3

接近该区域的法线。因此,使用

1

、

2

、

3

、

3

来描述每个点的局部几何结构。

(1)角点的归一化特征值向量。由于3个特征值和

3

对噪声和区域点云分布不敏感,鲁棒性更强,因此把特征点周围点云计算获得的3个特征值和第3个特征向量作为该特征点的描述算子。

设

是特征值的归一化特征值向量,则有

(36)

考虑到角点之间的搜索半径相同,而局部结构差异较大,且与3个特征向量

1

、

2

、

3

相比,3个特征值具有较好的旋转不变性。所以,使用特征值向量的两两之差来强化特征值对几何结构的描述。定义特征值之差向量为

=(Δ

… Δ

-1

)

(37)

式中Δ

=

+1

-

。

(2)角点的特征向量。本文在没有先验信息的情况下,将坐标原点作为视点。若

3

为指向视点方向,则设置法向量为

=

3

,否则

=-

3

。然后,将多尺度的法向量组合成矩阵

=[

…

]

(38)

由此,特征点的几何结构描述子定义为(

,

)。

3.2 基于阈值和描述子的角点配对与扩展

在进行角点配对与扩展时,本文定义了3个度量指标,分别是源点云与目标点云之间角点的描述子差异度、距离相似度和角度相异度。同时满足3个度量指标的一对角点才视为一组成功匹配对。

3

2

1 描述子差异度 当

和

特征值的描述子

之间的差值小于阈值

时,认为

和

之间存在对应关系,即

‖

-

‖<

(39)

执行完此步骤,即完成了角点的初始匹配,接下来进行角点匹配对扩展。

3

2

2 距离相似度 基于

={

,…,

}和

={

,…,

}中角点的几何结构描述(

,

),定义一个配对集合

={(

,

)}。对于任意的

∈

,角点与其支持点之间的距离为

=‖

-

‖。

在目标点云

中以距离相似度来搜寻

和

的对应关系,即

∈

∩{

||

′-

|<

}

(40)

式中:

′=‖

-

‖;阈值

反映了

的搜索范围。

3

2

3 角度相异度 角度相异度示意如图3所示。

对任意角点

∈

={

,…,

},定义角度

为

与

关于半径为

的法向量组成的夹角,即

(41)

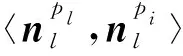
一个角点的支持区域内所有支持点构成的夹角向量为

=(

,…,

)

。

同理,目标点云

中也有与之对应的夹角

(42)

目标点云

中的夹角向量为

(43)

由此,

和

之间的角度相异度定义为

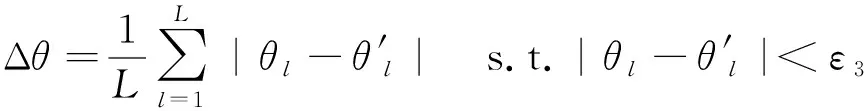
(44)

同时满足3个度量指标的点对

与

被认为是一对可靠的特征匹配对,更新配对集合

=

∪(

,

),否则配对集合

保持不变。

当完成源点云与目标点云的角点匹配及扩展后,利用成功匹配的点对计算两帧待配准点云之间刚体变换的初始值。为了进一步优化配准结果,本文将粗配准结果作为经典ICP算法的初始值(

,

)进行精配准,完成由粗到精的点云配准过程,得到最终配准结果。

4 实验及结果分析

4.1 实验设置及评价指标

为了验证本文算法的鲁棒性及有效性,在Stanford数据集

中的5个点云上进行了实验,并与5种经典算法进行了对比。所有算法均是基于PCL库实现编程

。实验环境为一台内存16 GB的4核2.6 GHz计算机。每种算法在每个数据集上均运行50次,取50次结果的平均值作为最终实验结果。

采用旋转误差

、平移误差

、算法运行时间

这3种点云配准领域常用的评价指标作为本文评价指标。这3种评价指标分别从点云配准算法的精度和效率两个方面对算法进行评价,且都是数值越小越好。旋转误差

和平移误差

的计算公式为

(45)

(46)

式中:

g,

、

g,

分别是旋转矩阵

、平移向量

的真值;

m,

、

m,

分别是旋转矩阵

、平移向量

的真值第

次刚性变换的估计值。

4.2 结果分析

4.2.1 特征提取算法结果对比 本小节实验是为了验证第2节自适应角点提取算法的有效性,在斯坦福Dragon点云上进行实验,该点云数据量为43 467。使用最远距离采样法进行下采样,预设所需点的数量为200,反馈200个采样点在原始点云中的索引。图4是基于最远距离采样的三维特征点分布,采样结束后将这些参照特征点的索引固定。

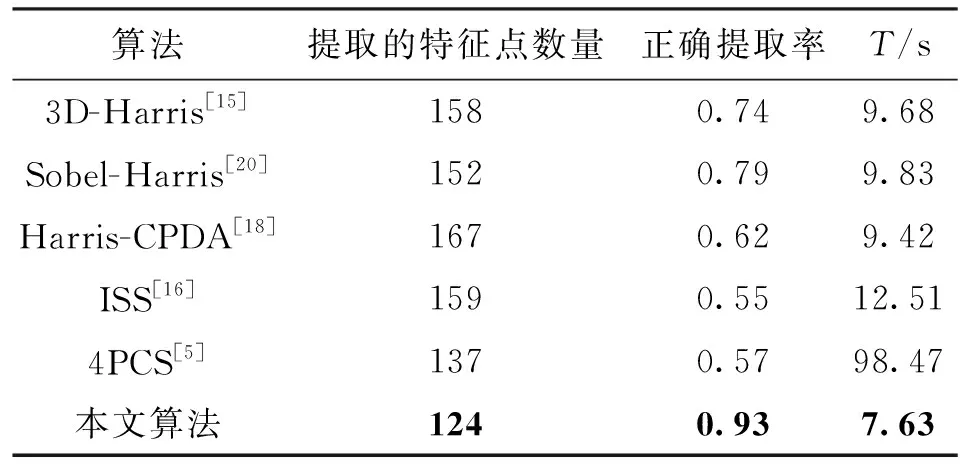
利用自适应角点提取算法和其他5种对比算法进行特征提取,返回特征点在原始点云中的索引。将每种算法提取到的特征点索引和参照特征点索引进行比对,索引一致则视为该特征点提取正确。计算出每种算法正确提取的索引数占200个索引的比例,作为特征的正确提取率。实验结果如表1和图图5所示。

从表1可以看出,相较于其他特征点提取算法,本文算法提取到的特征点数更少,特征点的正确提取率更高,说明本文算法提取到的角点具有更强的特征表征性,包含点云的几何信息更丰富。

实际上,在特征点提取时,3D-Harris

、Sobel-Harris

、Harris-CPDA

这3种算法需要手动设置角点响应阈值。通常需要多次实验才能找到合适的阈值。当更换点云后,阈值需要重新设定,算法实时性差。Harris-CPDA算法针对边界特征检测效果较差,如图5c所示。该算法受限于检测步长的阈值,导致多尺度下的圆角点区分相对模糊。

ISS算法

需要建立局部坐标系,并对所有点设置搜索半径,因此算法执行时间也较长。4PCS算法

需要在整个点云范围内寻找共面四点基,构建共面四点集合,所以计算复杂度高,耗时最长。

本文提出的基于正交梯度的3D-Harris算法能够在不降维的前提下对点云特征快速识别,最大化利用三维空间信息。同时,曲率约束能够自适应角点响应阈值,保证了算法的实时性和普适性。

4.2.2 粗配准算法结果对比 本小节实验是为了验证第2节自适应角点提取算法和第3节角点匹配与扩展算法的有效性,实验结果如表2～4所示。可以看出,本文算法能够兼顾精度和效率,得到最优的粗配准结果。

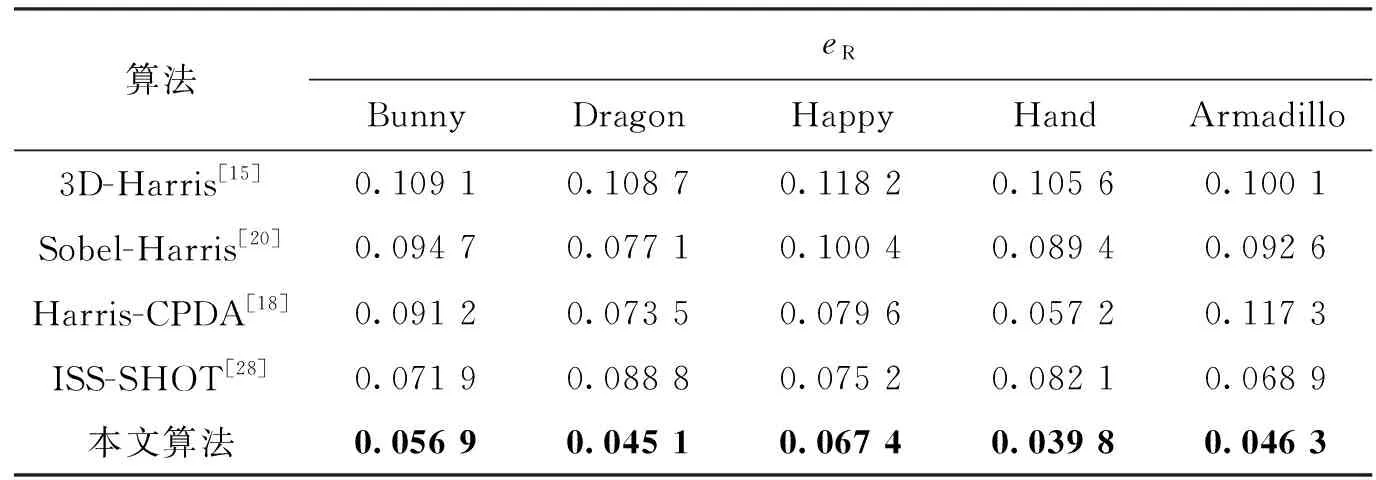
在对比算法中,3D-Harris和Sobel-Harris算法无法避免手动设置角点响应阈值,且阈值过小会丢失部分角点,阈值过大会识别出大量伪角点,不同点云中也没有一个普适的阈值。因此,算法精度和效率均较低。

Harris-CPDA算法运用累加点到弦距离之和原理。定义的弦长太小,会使步长受限产生角点误检;弦长过长,存在将多个局部峰谷描述成一个角点的情况。多尺度弦长会增加距离计算量,造成不必要的时间开销。

ISS-SHOT算法

利用余弦相似度在两帧点云之间搜索匹配点对,计算并统计32个子空间中各邻域点与查询点法向量之间的夹角余弦,并保存到直方图中。但是,该算法缺少剔除错误匹配点对的步骤,导致直方图易受错误匹配对影响,且统计夹角余弦耗时较长,配准效果不够理想。

本文的粗配准算法避免了人为设定角点响应值,会根据当前点所处的局部邻域的曲率计算出最适合的角点响应值。这一改进能够直接减少人工设定阈值的时间,提升算法效率。曲率约束算法能够普适各种点云模型,根据局部拓扑结构判断出该点是否为真实角点,避免角点漏检和误检。利用匹配点对的描述子、距离、夹角这3种特征,在待配准点云之间度量匹配点对的可靠性,可找出真实匹配关系,完成初始配准。

4.2.3 “粗配准+精配准”算法结果对比 本小节实验将4.2.2小节中的粗配准结果作为经典ICP算法的初始值(

,

)进行精配准,实验结果如表5～7所示。可以看出,本文算法配准结果最优。由于ICP算法对初值敏感,因此本文在获得最优粗配准结果的前提下,能够加速后续精配准的收敛。图6为本文粗配准算法结合ICP算法的配准结果。

5 结 论

(1)本文提出了一种完整、高效的自适应Harris角点特征描述、提取和匹配的点云粗配准算法。将正交梯度算子和高斯核函数的卷积计算融合到计算角点自相关矩阵中,能够完整使用三维信息实现角点检测。

(2)本文使用点云局部邻域的平均曲率

和高斯曲率

作为角点初步筛选条件,将曲率方差

作为阈值约束角点响应值,实现角点自适应筛选,避免了手动设置角点响应值和固定阈值造成的角点误判和漏判,提高了角点筛选效率。

(3)本文构建了角点几何结构的特征描述子(

,

)。结合阈值检测和描述子匹配,将角点匹配对进行扩展,从而完成源点云和目标点云之间粗配准。将粗配准结果作为ICP精配准步骤的初始输入,与对比算法相比,本文算法在5个点云上配准时间均为最短,配准误差最小。

:

[1]徐思雨, 祝继华, 姜祖涛, 等. 无序多视角点云的自主配准方法 [J]. 西安交通大学学报, 2018, 52(11): 134-141.

XU Siyu, ZHU Jihua, JIANG Zutao, et al. An automatic approach for multi-view registration of unordered range scans [J]. Journal of Xi’an Jiaotong University, 2018, 52(11): 134-141.

[2]RUSU R B, BLODOW N, BEETZ M. Fast point feature histograms (FPFH) for 3D registration [C]∥Proceedings of the 2009 IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2009: 3212-3217.

[3]BESL P J, MCKAY N D. A method for registration of 3-D shapes [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256.

[4]LI Yuqian, SU Guangda. Simplified histograms of oriented gradient features extraction algorithm for the hardware implementation [C]∥Proceedings of the 2015 International Conference on Computers, Communications, and Systems (ICCCS). Piscataway, NJ, USA: IEEE, 2015: 192-195.

[5]AIGER D, MITRA N J, COHEN-OR D. 4-points congruent sets for robust pairwise surface registration [J]. ACM Transactions on Graphics, 2008, 27(3): 1-10.

[6]MELLADO N, AIGER D, MITRA N J. Super 4PCS fast global point cloud registration via smart indexing [J]. Computer Graphics Forum, 2014, 33(5): 205-215.

[7]RUSU R B, BRADSKI G, THIBAUX R, et al. Fast 3D recognition and pose using the viewpoint feature histogram [C]∥Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ, USA: IEEE, 2010: 2155-2162.

[8]CHARLES R Q, SU Hao, KAICHUN M, et al. PointNet: deep learning on point sets for 3D classification and segmentation [C]∥Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway, NJ, USA: IEEE, 2017: 77-85.

[9]REZATOFIGHI S H, BG V K, MILAN A, et al. DeepSetNet: predicting sets with deep neural networks [C]∥Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV). Piscataway, NJ, USA: IEEE, 2017: 5257-5266.

[10]WANG Yue, SUN Yongbin, LIU Ziwei, et al. Dynamic graph CNN for learning on point clouds [J]. ACM Transactions on Graphics, 2019, 38(5): 1-12.

[11]SU Hang, MAJI S, KALOGERAKIS E, et al. Multi-view convolutional neural networks for 3D shape recognition [C]∥Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV). Piscataway, NJ, USA: IEEE, 2015: 945-953.

[12]LI Jiaxin, CHEN B M, LEE G H. SO-net: self-organizing network for point cloud analysis [C]∥Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway, NJ, USA: IEEE, 2018: 9397-9406.

[13]YEW Z J, LEE G H. 3DFeat-net: weakly supervised local 3D features for point cloud registration [C]∥Proceedings of the 2018 ECCV. Cham, Germany: Springer, 2018: 630-646.

[14]WEI Bo, YUAN Yuan, WANG Qi. MSPNET: multi-supervised parallel network for crowd counting [C]∥Proceedings of the 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Piscataway, NJ, USA: IEEE, 2020: 2418-2422.

[15]SIPIRAN I, BUSTOS B. Harris 3D: a robust extension of the Harris operator for interest point detection on 3D meshes [J]. The Visual Computer: International Journal of Computer Graphics, 2011, 27(11): 963-976.

[16]ZHONG Yu. Intrinsic shape signatures: a shape descriptor for 3D object recognition [C]∥Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops. Piscataway, NJ, USA: IEEE, 2009: 689-696.

[17]JASANI B A, LAM S K, MEHER P K, et al. Threshold-guided design and optimization for Harris corner detector architecture [J]. IEEE Transactions on Circuits and Systems for Video Technology, 2018, 28(12): 3516-3526.

[18]胡晓彤, 朱博文, 程晨. 基于Harris-CPDA的角点检测算法 [J]. 计算机工程与设计, 2021, 42(2): 504-511.

HU Xiaotong, ZHU Bowen, CHENG Chen. Corner detection algorithm based on Harris-CPDA [J]. Computer Engineering and Design, 2021, 42(2): 504-511.

[19]张见双, 张红民, 罗永涛, 等. 一种改进的Harris角点检测的图像配准方法 [J]. 激光与红外, 2017, 47(2): 230-233.

ZHANG Jianshuang, ZHANG Hongmin, LUO Yongtao, et al. Image registration method based on improved Harris corner detection algorithm [J]. Laser & Infrared, 2017, 47(2): 230-233.

[20]HAFIZ D A, YOUSSEF B A B, SHETA W M, et al. Interest point detection in 3D point cloud data using 3D Sobel-Harris operator [J]. International Journal of Pattern Recognition and Artificial Intelligence, 2015, 29(7): 1555014.

[21]HE X C, YUNG N H C. Curvature scale space corner detector with adaptive threshold and dynamic region of support [C]∥Proceedings of the 17th International Conference on Pattern Recognition: Vol.2. Piscataway, NJ, USA: IEEE, 2004: 791-794.

[22]张立亭, 黄晓浪, 鹿琳琳, 等. 基于灰度差分与模板的Harris角点检测快速算法 [J]. 仪器仪表学报, 2018, 39(2): 218-224.

ZHANG Liting, HUANG Xiaolang, LU Linlin, et al. Fast Harris corner detection based on gray difference and template [J]. Chinese Journal of Scientific Instrument, 2018, 39(2): 218-224.

[23]HARRIS C, STEPHENS M. A combined corner and edge detector [C]∥Proceedings of the Alvey Vision Conference. Manchester, UK: Alvety Vision Club, 1988: 23.1-23.6.

[24]苏步青. 微分几何学 [M]. 北京: 高等教育出版社, 1988: 1-279.

[25]梁增凯, 孙殿柱, 薄志成, 等. 样点邻域同构曲面约束的散乱点云曲率估计 [J]. 西安交通大学学报, 2018, 52(12): 50-56.

LIANG Zengkai, SUN Dianzhu, BO Zhicheng, et al. An estimation method for curvature of unorganized points cloud based on local isomorphic surface [J]. Journal of Xi’an Jiaotong University, 2018, 52(12): 50-56.

[26]Stanford University. The Stanford 3D scanning repository [DS/OL]. (2014-08-19)[2021-07-01]. http: ∥graphics. stanford.edu/data/3Dscanrep/.

[27]朱德海, 郭浩, 苏伟. 点云库PCL学习教程 [M]. 北京: 北京航空航天大学出版社, 2012: 1-402.

[28]李宇翔, 郭际明, 潘尚毅, 等. 一种基于ISS-SHOT特征的点云配准算法 [J]. 测绘通报, 2020(4): 21-26.

LI Yuxiang, GUO Jiming, PAN Shangyi, et al. A point cloud registration algorithm based on ISS-SHOT features [J]. Bulletin of Surveying and Mapping, 2020(4): 21-26.