基于点云聚类的垛型角点检测方法
张长勇,冯 冰,陈治华
(中国民航大学 电子信息与自动化学院,天津 300300)
0 引 言
目前,国内民航运输市场正处于快速发展阶段,不断增长的货物运输量,对机场的自动化水平提出了更高的要求,然而在多数机场的实际运行中,货物运输的装卸部分仍由人工操作完成。
为改善这一情况,在线码垛机械臂的研究和应用对实现货物运输的自动化装卸至关重要。为减少码垛过程中货物滑落、材质变形等对垛型的影响,本文针对垛型点云的角点检测展开研究,为码垛规划算法提供了真实的垛型空间模型,增强了码垛规划算法[1]的工程实践性。
近年来,国内外许多学者对点云的角点检测展开了研究。文献[2]对获取的三维点云进行边界提取、直线分割和直线拟合等过程,提取角点坐标;文献[3⁃4]认为角点在两条或三条直线的交点处;文献[5]将点云转化成对应的深度图,采用直线求交点的方法获取角点;文献[6]在室内门窗的三维点云模型中,采用点云转2D图像再与三维点云相结合的方法提取角点;文献[7]采用3D Harris角点检测的方法提取航天器的角点;文献[8]利用法向聚类和平面拟合筛选特征点,认为三个面的交点为角点;文献[9]提出一种基于局部重建的方法提取特征点,该方法利用共享近邻算法对局部三角形内的法向进行聚类,确定平面拟合的个数,认为同时属于2个面以上点为角点;文献[10]等采用高斯法向聚类的方法提取特征点,依据局部区域内法向聚类的个数判定特征点;文献[11]采用平面相交聚类分析的方法提取特征点。
综上所述,文献[2⁃4]采用直线求交点的方法,该方法对直线的拟合精度要求较高;文献[5⁃6]采用点云与深度图相结合的方法,该方法删除了高度信息,无法区分不同水平面的货物角点;文献[7⁃11]依据点云法向的变化信息检测角点,该方法适合于三个相交平面的点云均已获取的情况。
为了解决上述方法在垛型角点检测中的不足,本文在已获取垛型边界三维点云信息的基础上,分析了垛型角点在平面点云中呈现的角度特性,提出了一种基于点云聚类的垛型角点检测方法。
1 垛型角点检测方法
1.1 候选角点获取
在提取候选角点时,本文采用轮廓尖锐度角点检测算法[12]中角度阈值检测的思想,并对其依据支撑臂长计算角度的方法进行改进。首先从垛型的三维点云边界上任选三维点A(如图1所示),然后通过三维kd⁃tree的半径搜索,得到以A为圆心,r为半径的圆内三维点云。

图1 垛型边界点云数据局部放大图
将图1中圆内部A点两侧的点降维成二维点,并采用随机采样一致性算法在A的两侧分别拟合出一条左直线与一条右直线。然后,依据如下公式计算两直线夹角α的余弦值。
设两直线的拟合方程为:
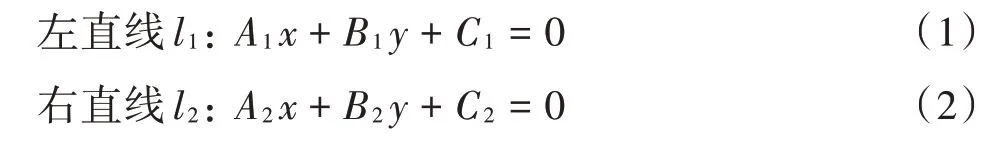
则:
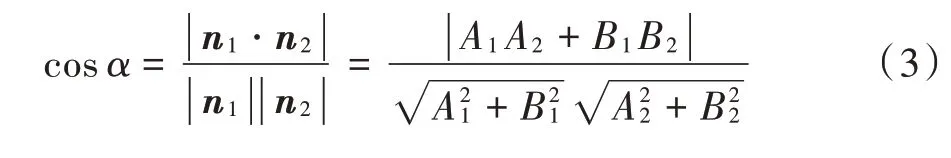
式中:n1为直线l1的法向量;n2为直线l2的法向量。根据理想角点处的角度特征,垛型角点处cosα的值接近于零。定义一个变量S=1-cosα,S值越大,说明该点越有可能成为候选角点。计算垛型边界数据集B={X i}上每一个点的S值,设定阈值T,当S(X i)>T时,将X i标记为候选角点。
改进的尖锐度角点检测算法会抑制部分普通边界点被误判为角点的情况。如图2所示的普通边界点B,采用尖锐度角点检测算法得到的角度近似为直角(如两虚线构成的夹角所示),判定B为角点;采用改进算法拟合的两直线接近平行(如直线l1与l2所示),判定B为边界点。由此可知,改进角点检测算法会在一定程度上减少普通边界点被误判为角点的数量。

图2 角点误判示意图
1.2 候选角点聚类
采用改进的尖锐度角点检测算法时,会在同一角点区域获得多个符合判定条件的点,从而得到存在冗余点的候选角点。为了对属于同一角点区域的候选角点进行合并计算,通过改进的快速密度峰值搜索算法(Clustering by Fast Search and Find of Density Peaks,CFSFDP)结合K⁃means算法对候选角点进行聚类,以区分不同角点区域的候选角点。
1)改进的CFSFDP算法自动确定簇中心点
CFSFDP算法[13]假设簇中心是局部密度最大值,并且簇中心远离其他更高密度的点,为了寻找符合假设的簇中心点,计算局部密度ρi与相对距离δi,然后依据ρi,δi画出决策图,最后人为依据决策图将局部密度和相对距离同时较大的数据点作为簇中心点。文献[14⁃15]计算一个将ρ值和δ值综合考虑的变量γ,γi=ρiδi,然后,通过人工观测或利用γ值存在非线性变化这一特征来区分簇中心点与非簇中心点。
本文对排除离群点的γ值降序排列后,发现在簇中心点之间,非簇中心点之间,γiγi+1值变化平缓,但从簇中心点过渡到非中心点时,会出现较大的跳跃。因此,定义如下中心判别式以实现中心点的自动提取:
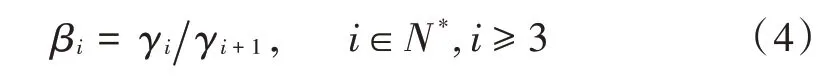
根据上述判别式可以得出,maxβ对应的点即为簇中心与非簇中心的区分点,排在最大值之前的点即为簇中心点。
2)CFDP结合K⁃means聚类候选角点
K⁃means聚类算法需要随机选取k个点作为初始聚类中心进行迭代操作,但由于垛型的角点个数未知,无法初始化k值。因此,通过改进的CFDP算法对候选角点进行预处理,将获得的簇中心点作为K⁃means的初始聚类中心,以保证K⁃means的聚类效果。融合算法具体的步骤如下:
Step1:改进的CFDP初始化K⁃means的k值与初始聚类中心C={C1,C2,…,C k}。Step2:计算候选角点中点与聚类中心的距离,将其划分到距离其最近的聚类中心所属的集合,分配依据为:

式中:s i为第k类候选角点;j=1,2,…,N;i=1,2,…,k;p≠i;t为时刻。
Step3:根据Step2的分配结果,更新聚类中心:
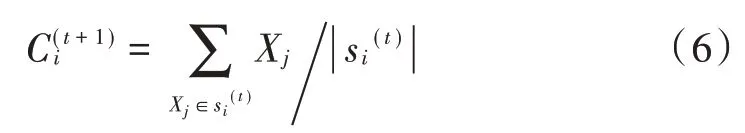
Step4:若前后两次聚类中心的差值小于设定的阈值ε,即,则算法结束;否则,转向Step2。
1.3 候选角点合并
通过CFDP⁃K⁃means算法对垛型候选角点进行聚类,得到同一角点区域的候选角点。假设同一角点区域候选角点的集合为H:
h1(x1,y1,z1),h2(x2,y2,z2),…,h n(x n,y n,z n)∈H,n≥2 (7)式中n表示同一角点区域候选角点的个数。通过密度值法[12]计算同一角点区域内每个候选角点的密度值,采用点h(xmaxρx,ymaxρy,zmaxρz)作为垛型最终角点坐标。其中,xmaxρx表示在x方向上取密度值最大的x作为最终角点坐标的x值,同理可得ymaxρy,zmaxρz。
综上所述,本文方法流程图如图3所示。
2 实验结果分析
为验证本文方法的可行性,采用Kinect一代相机,分辨率为640×480的深度像机获取垛型的三维点云数据。采用C++编程语言,VS2015编译环境,在硬件参数Intel CoreTMi5⁃7200U CPU@2.50 GHz 4.00 GB,WIN10 x64操作系统进行实验。
实验搭建如图4所示的纸箱垛型,在其上方高约1.4 m的位置安装一台相机,通过直通滤波得到对应的三维点云如图5所示。
2.1 候选角点分析
1)候选角点提取分析
采用改进的尖锐度角点检测算法提取垛型的候选角点,以90°-6×n≤α≤90°+6×n(n=0,1,2,3)为α变化范围;r=10+10×n(n=0,1,2),为r的取值进行实验。不同参数下的提取状况如表1所示,其中部分参数下的提取效果图如图6所示。

图3 本文方法流程图

图4 实验垛型图

图5 垛型三维点云图
由表1可知,角点的个数随着r值的增加与α范围的增大而增多;由图6的效果图可以看出,图6a)比图6b)的候选角点数量少,且图6a)比图6b)漏检了4个角点区域;图6c)与图6b)相比,图6c)中出现大量边界点。因此,选取r=20,α=84°~96°为角点检测的参数范围。
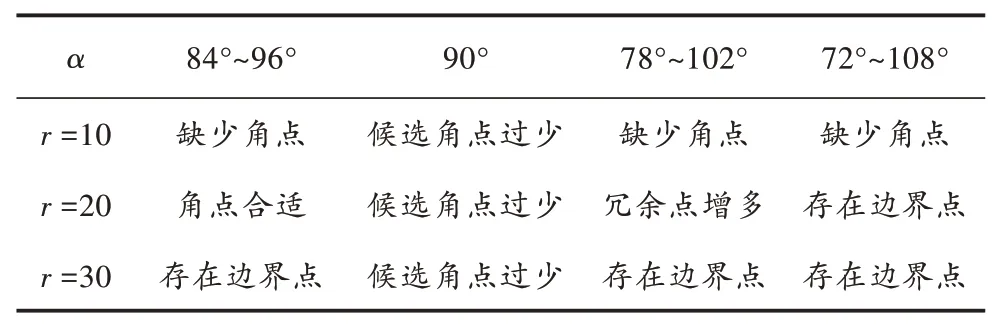
表1 不同参数下候选角点提取效果对比

图6 部分参数下的候选角点效果图
2)候选角点聚类分析
由CFDP算法获得候选角点的簇中心点,如图7中的“+”所示,从图7中可以看出,14个候选角点区域获得了14个初始簇中心,验证了CFDP算法在候选角点数据集上的有效性。

图7 初始簇中心
候选角点集的聚类结果如图8所示,从图8中可以看出,14个候选角点区域中每一个区域内的点都具有相同形状的符号,验证了CFDP⁃K⁃means算法的良好聚类结果。

图8 候选角点聚类结果
2.2 误差分析
将本文算法计算的角点坐标与人工测量的角点坐标进行对比,并计算估计误差,以验证本文所提算法的准确性。估计误差计算公式为:

式中:e表示估计结果误差值;(x,y,z)为角点的真实坐标值;(x̂,ŷ,ẑ)是计算的角点坐标,误差结果如表2所示。
从表2可以看出,通过本文所提方法计算的垛型角点坐标误差在8 mm以内。这是由于前期采用的数据预处理以及边界提取的方法还有待改善,导致进行垛型角点检测时出现一定的误差。
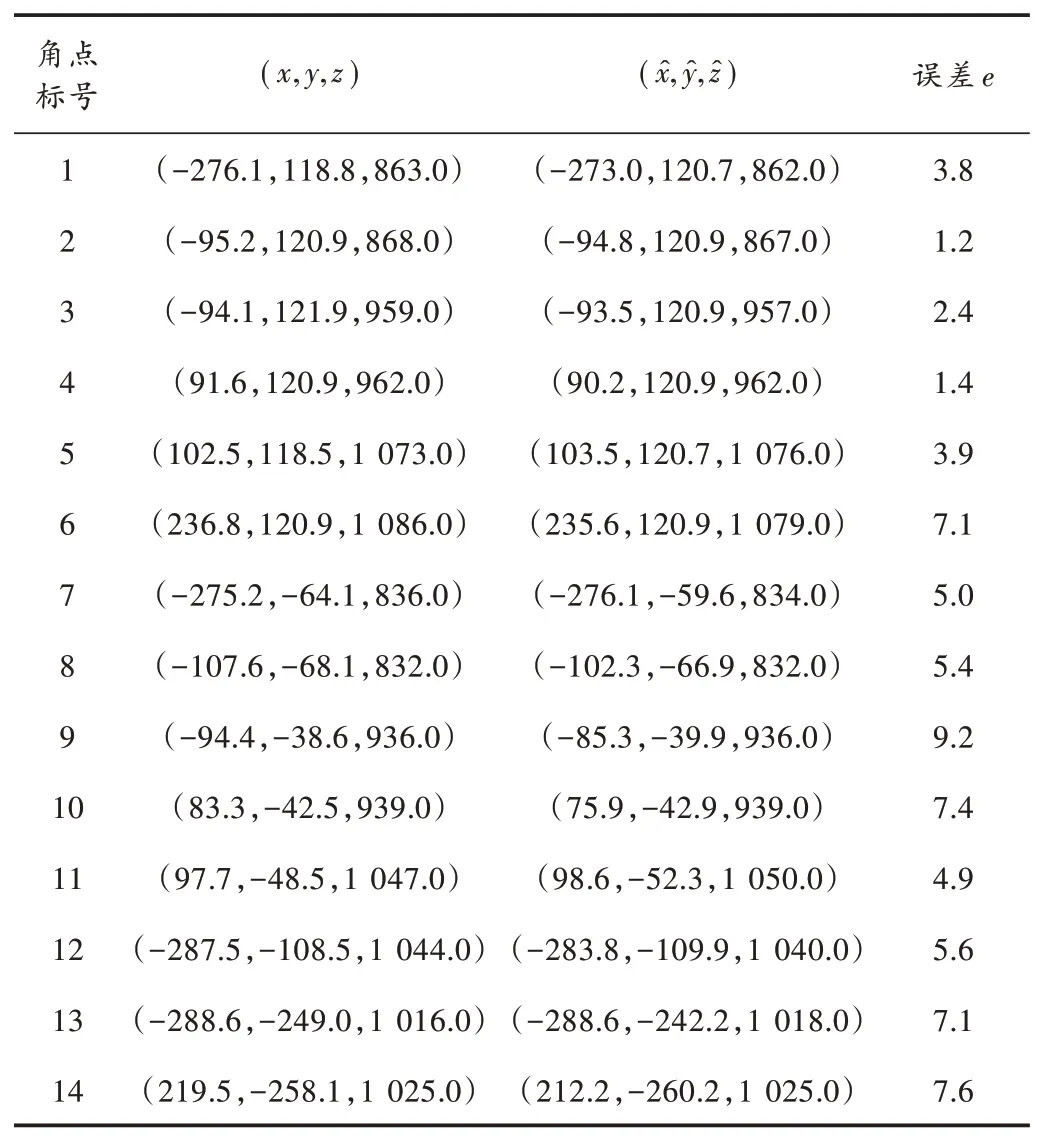
表2 货物垛型对应的角点坐标数据 mm
3 结 论
本文主要研究垛型的角点检测,提出一种基于点云聚类的垛型角点检测方法。该方法在已获取垛型边界三维点云信息的基础上,依据局部区域内两直线的角度值获取候选角点,减少边界点被误判为角点的可能性;然后对候选角点采用先聚类再合并的计算方式,确保角点计算的准确性。最后,通过搭建真实的纸箱垛型进行实验,结果表明,本文所提方法能有效地检测出垛型的特征角点。

