“互联网+”背景下高等数学一流课程建设的探索研究

摘要:为了提升高校高等数学教学水平,实现对高等数学精品课程的建设,以“互联网+”作为研究背景,开展高等数学一流课程建设的探索研究。该文通过分析高等数学课程建设现存问题,及“互联网+”对高等数学一流课程建设的促进作用,提出基于多维角度设计高等数学一流课程建设标准的方式,将具有协同性的课程内容融合为一个章节,在此基础上,删除课程中的重复性内容。建设高等数学一流资源库,对课程教学内容进行重构,并构建融合过程性的高等数学一流课程教学体系,整理学生的学习成果,以此作为依据,评估建设的课程是否符合一流标准。
关键词:“互联网+”背景;高等数学;课程标准
中图分类号:G642.307 文献标识码:A
文章编号:1009-3044(2022)03-0116-02
开放科学(资源服务)标识码(OSID):
高等数学课程是一门相比初等数学课程与中等数学课程而言,难度较高、内容较复杂的课程,其教学内容中不仅涉及中等数学内容中的几何内容与代数内容,同时也包括难度较高的数列内容、微分方程内容、空间几何解析等内容。高等数学课程是各大高校,针对理工科学生开设的一门基础性课程,高等数学课程教育的质量也是评估高校素质教育能力的关键指标。为了提高教育院校在市场的地位,应当加强对高等数学一流课程建设的关注[1]。在信息化技术广泛应用于教育市场的背景下,“互联网+”成为各大高校与多个教育组织机构的关注热点,为了满足时代发展对教育素质改革提出的要求,多个教育单位纷纷将其自身的教育课程与互联网技术进行融合,希望通过此种方式提高自身在教育市场的竞争力。但综合现如今我国教育市场的发展现状可知,大部分高校引进“互联网+”技术,均是为了打造线上教学平台,拓宽课堂教育的覆盖范围,但仍须进一步探究。
1 高等数学课程建设现存问题
为了满足新时期教育市场发展对高校数学教学改革提出的要求,有关教育部门深入到了对高等数学一流课程建设的研究中,综合现如今高校开设的课程内容可知,传统的高等数学教学课程已无法满足或响应时代发展对其提出的需求。高校为了保障教育过程的连续性,通常会在教育中严格按照课本内容对学生进行教育指导。尽管此种方式可实现对学生的基础性教育,但却忽视了在此过程中对学生思维能力与创造能力的培养[2]。此种课程使学生在学习中,仅能按照规范化的理论解题方式,套用公式完成算数过程,但却不懂在学习过程中对某些内容的“举一反三”,因此,此种教育方式也无法达到对学生创新性能力与发散性思维的培养,导致高校预计的课程教育成果与实际输出的教育成果存在显著差异。
除上述提出的问题,在对学生进行课程教学普查时发现,调查的学校内超过半数的学生表示,现有的高等数学课程根本无法满足其自身对于学习的要求,大部分课程教學内容呈现一种碎片化现象,十分不利于学生在学习中对某些知识点的集成管理。并且,教师在教学中,也没有对碎片化的教学内容进行整合,导致学生在完成学习后,根本无法将学会的知识点串联在一起,影响学生在学习中对某个知识点的理解。
2 “互联网+”对高等数学一流课程建设的促进作用
将“互联网+”与高等数学课程建设工作进行融合,其目的在于设计精品或一流课程。考虑到网络上现有的高等数学成功教学案例过多,倘若教师一味地引进其他高校的教学案例或课程内容,没有考虑到其内容是否与学习需求适配,不仅无法达到预计的教学效果,甚至会在一定程度上对教学工作起到适得其反的作用。而在“互联网+”技术的应用下,高校可通过学生在线上反馈的信息,或通过学生的综合考评成绩,实时掌握学生的学习进度,并以此为依据,及时调整课程建设方向与课程内容,使建设的高等数学教学内容与学生学习需求更加匹配[3]。在“互联网+”背景下,高校高等数学课程建设势必要发生改革,也必然会走向一个新的建设方向。
3 “互联网+”背景下高等数学一流课程建设策略
3.1 基于多维角度设计高等数学一流课程建设标准
高等数学一流课程建设工作是一项系统性与综合性的工作,要落实此项工作,提升高等数学课程的建设质量,需要在建设前,及时掌握学生对于课程的学习需求,并以学生需求为根本,从多维角度,设计高等数学一流课程建设标准[4]。
在完成对高等数学课程教学章节或教学框架的设计后,需要将与此相关的内容整理成电子版文件,上交到地方教育部门进行课程基础设计的审核[5]。并在文件中附上设计课程时,高校所有参与此项工作的核心人员名单、课程设计思想、课程教学目标、课程教学目标等。只有满足上述提出的多项内容,才能确保设计的高等数学课程符合教育部门提出或制定的一流标准。一流的高等数学课程,是集成一流教师团队、一流教学方法、一流指导内容、一流中心思想的特色化师范课程,因此,课程框架应具有现代化、导向性等特点。
3.2 “互联网+”背景建设高等数学一流资源库
在我国高等职业教育不断扩招的背景下,各大高校均将教育的重点与核心置于对学生管理层面,此种行为却在一定程度上忽视了对课程内容的建设。为了实现对高等数学一流课程的建设,本章将以“互联网+”作为研究背景,采用建设高等数学一流资源库的方式,对课程教学内容进行重构[6-8]。在此过程中,应明确高等数学课程是一门系统性与逻辑性较强的课程,因此,应将课程建设的核心定位在对学生逻辑思维与算数思维的培养层面。要满足上述提出的要求,需要整合教育市场内多个试点教育院校的课程教学内容,在此基础上,增强不同课程内容的实践性。例如,可在设计教学内容的过程中,尝试将一些专业学科内容与高等数学教学内容进行融合,使一些抽象性的教学内容生活化,以此种方式,使理论性较强的课程更加贴近于实际,从而辅助学生更好地理解知识点。
在建设资源库过程中,除了要注意对成功教学案例的导入,还应当在此基础上,建设一个可实现在互联网平台上运行的电子资源库。电子资源库内应包含的内容可参照表1。
按照上述表1中内容,对高校高等数学一流资源库内容进行设计,在此基础上,对接资源库与互联网,学生不仅可以在指定空间内进行资源的检索,同时也可以通过资源库进行拓展性知识的学习。总之,在“互联网+”背景下,一流课程建设过程是一个相对自由的过程,不仅教师可以及时根据教学进度调整课程内容,同时,学生也可以根据其自身对知识点的理解与记忆情况,对教师进行教学反馈,以此种方式,进一步实现对课程内容的规范化设计。
3.3 构建融合过程性的高等数学一流课程教学体系
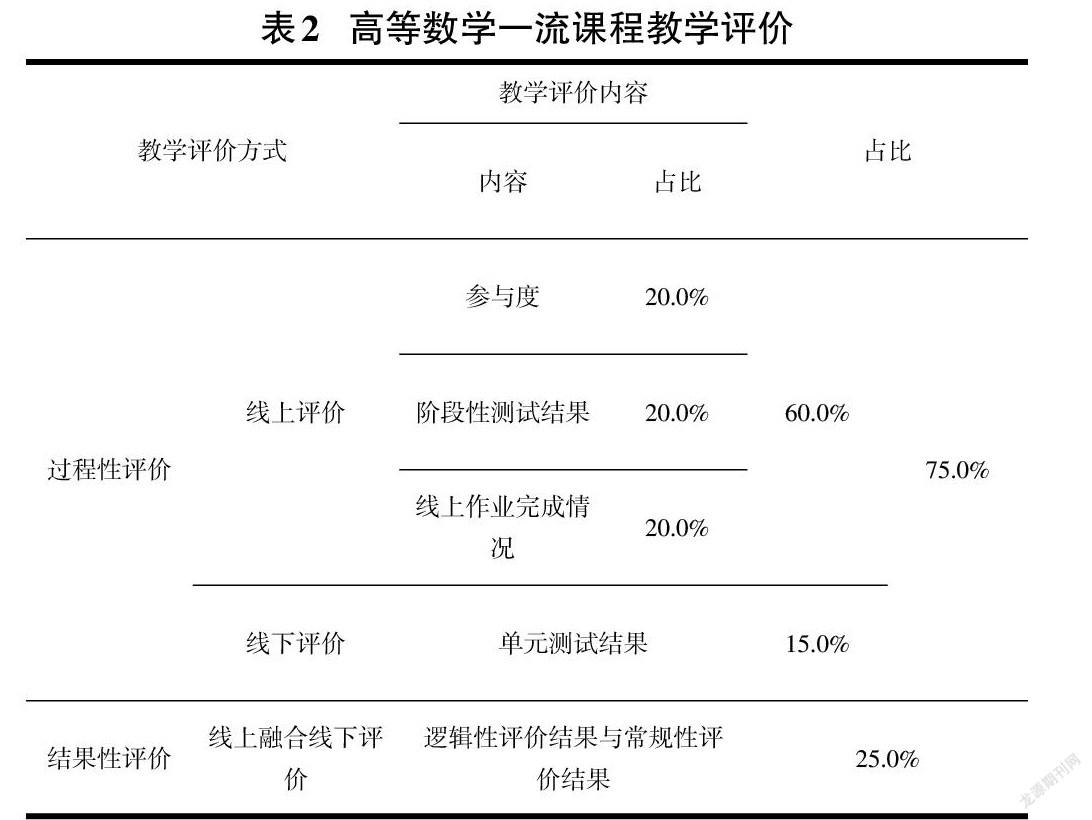
构建一体化的高等数学课程教学体系,是高等数学一流课程建设的核心任务,为了满足“互联网+”背景下,教育市场对高校教学工作实施提出的要求,高校可结合互联网教学平台的应用,打造一种融合线上与线下的过程性教学体系。利用高校现有的线上教学平台,对学生进行高等数学基础性课程内容的讲解,在学生具备了一定学习基础后,利用有限的课堂教学时间内化知识点,以此种方式,实现对原有课程教学的拓展。也可通过在课程建设中发现的学生学习盲区,对高等数学课程中涉及的知识点进行专项讲解,并利用资源库提供教学的多种资源,反复引导学生进行知识点盲区的训练,以此种方式实现对集成型教学体系的构建。为了确保高校建设的一流课程在实际应用中,具有一定的价值,可在完成上述相关工作的基础上,增设一个针对课程教学成果的评价体系,即根据学生在学习中的反馈信息与测评结果,对课程内容进行反复整改。考核方式如下表2所示。
按照上述表2中内容,整理学生的学习成果,在此基础上,综合反馈的结果,评估高校建设的高等数学课程是否属于一流或后期是否需要调整与变更。以此种方式,完成对课程的建设工作。
4 结束语
对于高等素质教育院校而言,“互联网+”技术的引进,实现了对传统教育教学的有效突破,摆脱了教学环境单调、教育模式单一等问题,实现了教育成果的输出,提高了产业发展的均衡化与教育指导行为的个性化。为了进一步提高素质教育的水平,本文以“互联网+”作为研究背景,从课程建设标准、课程内容、课程教学体系三个方面,对高等数学一流课程建设展开研究,并希望通过此次的研究,提升各大高校高等数学的教学水平,实现建设的精品课程更符合学生学习需求,从而使教学水平达到一种阶梯式上升的趋势。
参考文献:
[1] 周素静,刘冬华,乔铁,等.“互联网+教育”背景下大学生学习有效性调查研究——以高等数学课程为例[J].郑州铁路职业技术学院学报,2021,33(2):73-76.
[2] 赵玲弟.职业院校“高等数学”课程“一条主线,分散补差”教学模式研究与实践——以“高等数学”课程为例[J].工业和信息化教育,2021(4):65-69.
[3] 范慧玲,曹鸣宇,袁玉萍,等.《高等数学》课堂教学中融入课程思政案例——以《定积分的概念》为例[J].科技资讯,2021,19(8):158-160.
[4] 周勇,周燕,吕书龙,等.少数民族学生数学公共基础课精准帮扶模式的优化与实践——以福州大学高等数学课程为例[J].高等理科教育,2020(6):75-81.
[5] 宋艺.课程思政背景下《高等数学》课程教学设计与实施——以“增长率的计算与比较”为例[J].長沙民政职业技术学院学报,2020,27(4):105-106.
[6] 王俊彦.独立学院数学课程教学改革方案探讨[J].吉林省教育学院学报(上旬),2013,29(5):46-47.
[7] 王俊彦.浅谈独立学院高等数学学困生的转化策略[J].中国科教创新导刊,2011(34):67.
[8] 张玥,邹健,张伟,等.人工智能专业“高等数学AI”课程教学探讨——以安徽工程大学为例[J].湖北第二师范学院学报,2021,38(2):89-93.
【通联编辑:张薇】
——依托《课程标准》的二轮复习策略

