核心素养视域下小学生数学思想方法的渗透

晏小艳

【摘要】对于学生而言，在数学学习中能够熟练掌握基础知识固然重要，但如果能在数学学习中掌握数学思想方法则更有价值。数学学科思想方法的种类有很多，在众多的数学思想方法中，转化思想尤为重要。如果学生能够了解转化思想，并能灵活地运用它，学生的数学学习一定会变得轻松、有效。

【关键词】渗透 转化 思想 路径

在生活中，我们经常会遇到一些棘手的问题，但这些问题最终可以用一些小技巧来处理。广为流传的经典故事“曹冲称象”，告诉我们在遇到难题时可以试着转换思路解决问题，而不是遇见难题就轻易放弃。

转化思想是最基础、最实用的解决问题的策略之一，学生在平时的学习过程中已经对转化思想有了一定的认识，但是这些认识是非常零散、粗浅的，需要我们教师有意识地渗透、提炼，进而内化为学生的一种思想方法，让学生能够灵活地运用转化思想解决问题。

小学生因年龄小，在学习时往往缺乏耐心，这就对教师提出了更高的教学要求。在教学过程中，教师需要把握合适的时机，对学生进行转化思想意识的引导，使学生形成良好的思维习惯，自觉地将转化思想运用到学习中去。

一、在学习新知识时构建转化思想

任何一种新知识，总是在旧知识的基础上进行发展和转化的。在实际教学中，教师要巧妙地联系学生已经学过的旧知识，引导学生自主地产生转化的需要，让学生利用“旧知识”解决“新问题”，让转化思想无声地扎根于学生的心中。

1.在“几何”教学中的渗透

在小学阶段，计算平面图形的面积教学中，把学生不熟悉的平面图形转化成学生熟悉的平面图形，就运用了转化思想。

在平面图形面积公式的教学中，公式的推导过程应该是教学的重点。教师应该及时引导，给学生一定的时间，让学生通过合作探究，从已经学过的旧知识迁移到新知识。在教学“平行四边形的面积”相关知识时，教师可以先让学生回忆长方形面积计算公式的推导过程。在这个过程中，教师在适当的时候进行启发，指导学生根据之前的学习经验，通过这一系列的操作、观察、比较、分析、推理的过程，得出结论：平行四边形的面积等于底乘高。

有了推导的经验，学生在计算其他平面图形的面积时，就会想到把新知识转化成旧知识进行研究。学生充分体验了转化思想策略在学习新知识过程中的作用，积累了学习经验，促进了思维发展。

2.在“数与运算”教学中渗透

数与运算贯穿于小学数学学习的全过程，一到六年级的数学教材中都有相关的内容，这些知识点的学习大多用到了转化思想。

有这样一道题目：一个羽毛球2.4元，如果有86.4元，可以买多少个羽毛球？学生列出算式：86.4÷2.4。教师引导学生观察这个算式跟以前学过的算式有什么不同，学生通过回忆、对比发现，之前计算除法算式时，除数是整数，这道算式中的除数2.4是小数。教师引导学生，问：“我们该怎样处理这道算式？可以把除数2.4转化为24，被除数86.4转化为864。这样就把‘86.4÷2.4’转化为了‘864÷24’。”

这道算式转化成了整数除以整数，学生在计算过程中感受到知识之间是有联系的。在学习探究的过程中，为什么要转化，根据什么进行转化，如何转化，转化时要注意什么，这些都是本节课的教學重点。学生亲身经历了观察、发现、思考并运用转化思想方法解决问题的过程，激发了探究新知的欲望。

3.在运算定律中渗透

苏教版小学《数学》四年级（下册）中有运算定律的相关内容，学生首次接触运算定律，体会到运算定律在计算中的价值。苏教版小学《数学》五年级和六年级的教材中均有小数和分数的四则混合运算相关内容。在学习关于小数的运算定律时，学生可以运用整数运算定律的经验，把小数转化成整数来解决问题。六年级学生学习分数运算定律的相关知识时，虽然学习的难度加大了，但是学生已经有了一定思维基础，对这部分知识点的学习，转化思想方法得到了充分的体现。

4.在性质和规律中渗透

学生在学习“分数的基本性质”相关知识时，运用“商不变的规律”进行转化;学生在学习“比的基本性质”相关知识时，运用“分数的基本性质”进行转化。这些都体现了转化策略的运用。“转化”策略其实就是将较复杂的问题转化成较简单的问题，把新的问题转化成已经得到解决的问题。学生在探究新知的过程中，数学能力得到培养，数学素养得到提升。

二、在解决问题中实践转化思想

1.化抽象问题为直观问题

学生在解决实际问题时，若题目比较抽象，学生往往难以理解题意，不能迅速找到数量之间的关系，没有解题的思路。

例如：植树节到了，某小学六年级组织学生植树，买了银杏、红李和桂花三种小树苗，红李比银杏便宜20元，桂花比银杏便宜48元，一共用去205元，三种小树苗的单价各是多少？

学生刚看到题目，发现条件只有“总价”和“红李比银杏便宜20元”“桂花比银杏便宜48元”，无法迅速找到解题思路。这时，我们可以将抽象问题转化为直观的线段图来分析、解答。

2.化复杂问题为简单问题

在计算“992+993+994+995+996”时，学生发现这道题如果按计算顺序逐一相加，不仅耽误时间，还容易算错。如果仔细观察，会发现一共有5个数，后面的每个数比前一个数多1，以中间数为标准，用“割补”的方法将它们转化成“994+994+994+994+994”，这样算既节省时间，又不容易出错。

3.化特殊问题为一般问题

有这样一道题目：某小学开展手抄报展示活动，六年级共收到手抄报78份，贴在9块展板上。小展板每块贴6份手抄报，大展板每块贴10份手抄报。大展板和小展板各有多少块？

我们可以把两种展板转化为一种展板来解决。如果9块展板都是大展板，10×9=90份，比78份多了12份;如果9块展板都是小展板，6×9=54份，比78份少了24份。教师让学生思考多了12份和少了24份的原因是什么，让学生从中找出解题思路。

三、在总结时渗透，体会转化思想

在每个课时、每个章节教学结束后，教师要指导学生对本课时、本章节的学习内容进行总结，回顾学习过程中运用了什么思想方法，运用转化思想解决这个问题时有什么优势，使学生充分地感受转化思想在数学学习中的价值。

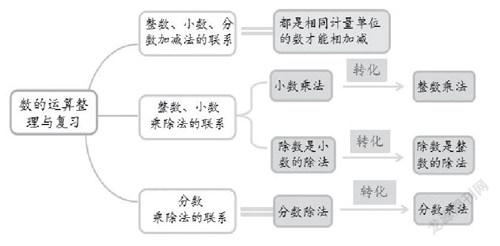
在学习“分数乘除法”的相关知识后，教师可以指导学生从整数、小数和分数三类数的运算进行梳理，利用画思维导图的方式，将相关知识点的联系展现出来，使学生明白新知识和旧知识之间是怎样转化的。

总而言之，转化思想对于小学生来说非常实用。加强转化思想在教学各环节中的渗透，让学生体会到转化思想的价值，可以让学生从被动学习变为主动学习，最终灵活运用转化思想，提高学习效率。

（作者单位：江苏省盱眙县桂五镇中心小学）

3199500338232