基于分数阶忆阻器的混沌电路分析与设计
吴朝俊 ,祁永伟 ,刘 璋 ,杨宁宁
(1.西安工程大学 电子信息学院,陕西 西安 710048;2.西安理工大学 电气工程学院,陕西 西安 710048)
20 世纪70 年代,由科学家蔡少棠[1]提出了一种描述电荷量与磁通量关系的非线性电路元件(忆阻器),该元件成为了除电阻、电容和电感之外的第四种基本电路元件。自2008 年Hewlett-Packard(HP)实验室的研究员Strukov 等[2]成功研制出忆阻器实物以后,忆阻器的研究与应用受到了来自不同研究领域专家和学者们的极大关注。目前,忆阻器被广泛应用到人工智能[3-4]、神经网络[5-8]、电子芯片[9-10]、混沌电路[11-14]等不同领域中。一般来说,若一个电路端口的伏安特性符合文献[15]中所描述的三个基本特性,则该器件可以定义为忆阻器。文献[16]提出了一种由二极管桥级联一个RC 滤波器的广义忆阻器,通过利用不同周期激励下的收缩磁滞回线,对忆阻器的特性进行分析研究。文献[17]提出了基于二极管桥和串联RL 滤波器的忆阻电路模型,通过建立相应的数学模型以及实验验证,表明该电路模型符合忆阻器的基本特性,为实际的电路设计与应用提供了基础。
忆阻器具有记忆特性以及非线性特性,因此很适合用于构造具有复杂结构的混沌电路,并且基于忆阻器的混沌电路通常可以表现出相对复杂的动力学特性。例如,文献[18]提出了一个基于有源忆阻器的最简单的混沌电路。文献[19]通过平滑磁通控制型忆阻器代替蔡氏电路中的二极管,构成了新型的忆阻混沌电路。文献[20]报道了具有无限多个稳定平衡点的四维忆阻混沌电路,并分析了电路中表现出的复杂动力学特性。
过去对于忆阻混沌电路的研究大多都是基于整数阶的电路模型,对于分数阶忆阻混沌电路的报道较少。而分数阶微积分是一种研究任意阶次微分与积分算子的数学理论,有关研究表明,分数阶微分方程能够更加准确地描述自然现象,因此将忆阻混沌电路推广到分数阶可以得到更精确的电路模型。
为了研究分数阶忆阻器的电路特性,本文建立了一种由二极管桥级联RLC 滤波器的分数阶广义忆阻器,并对分数阶忆阻器的动态特性进行了分析。进一步,在蔡氏振荡器的电路模型基础上,将分数阶广义忆阻器模型引入到振荡器中,并将电路模型中的所有动态器件推广到分数阶次,建立了分数阶忆阻混沌电路模型。通过研究电路参数对系统动力学的影响,表明了分数阶系统具有复杂的动力学行为。最后,在PSpice 中搭建了分数阶忆阻混沌电路的等效电路模型,并进行仿真实验,实现了基于分数阶广义忆阻器的混沌电路。
1 基于分数阶广义忆阻器的混沌电路
1.1 分数阶微积分理论
分数阶微分算子的三种常用的定义是Grunwald-Letnikov(GL),Riemann-Liouville(RL)和Caputo 定义。在零初始条件下,Caputo 定义的分数阶导数和整数阶微分具有相同的形式,并且具有明确的物理意义,适合工程问题的求解,本文的分数阶模型都采用Caputo 定义的微分算子。Caputo 定义的分数阶导数为:
式中:n表示正整数;t表示时间变量;τ表示积分自变量;q表示分数阶阶次;表示函数f(t)的q阶Caputo 微分算子;f(n)(t)表示f(t)的n阶导数;Γ 表示Gamma 函数,它的表示形式为:
Caputo 分数阶导数的Laplace 变换可以表示为:

式中:S表示复频率;k表示正整数变量。
通过式(3)可以看出分数阶导数只涉及函数f(t)及其整数阶导数的初值。当函数f(t)的初始值为0 时,公式(3)可以简化为:
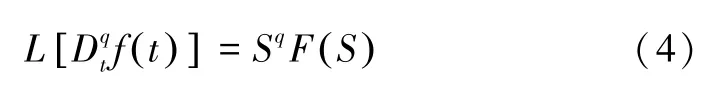
1.2 分数阶广义忆阻器模型
文献[21]提出了一种由电容、电感和二极管桥构成的广义忆阻器,其电路结构如图1 所示。从图1 可以看出,该忆阻器电路由四个二极管、一个电感和一个电容构成。其电路结构简单,可以用一个电路实现。其中图1(a)表示忆阻器的电路模型,图1(b)表示忆阻器的等效符号。
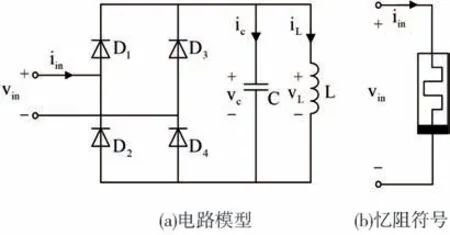
图1 广义忆阻器模型Fig.1 Generalized memristive model
实际中的电容和电感都表现为分数阶特性,本文在图1 的广义忆阻器电路模型基础上,将电容和电感扩展到分数阶次,并且并联一个电阻与二极管桥电路构成一种分数阶广义忆阻器,其电路等效模型如图2所示。
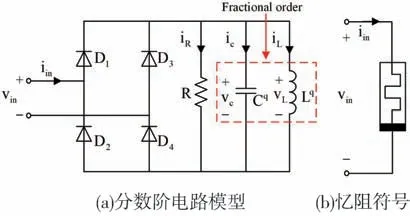
图2 分数阶广义忆阻器模型Fig.2 Fractional-order generalized memristive model
对于图2 所示的分数阶广义忆阻器电路模型,根据电路原理以及基尔霍夫定律,其数学模型可以表示为:
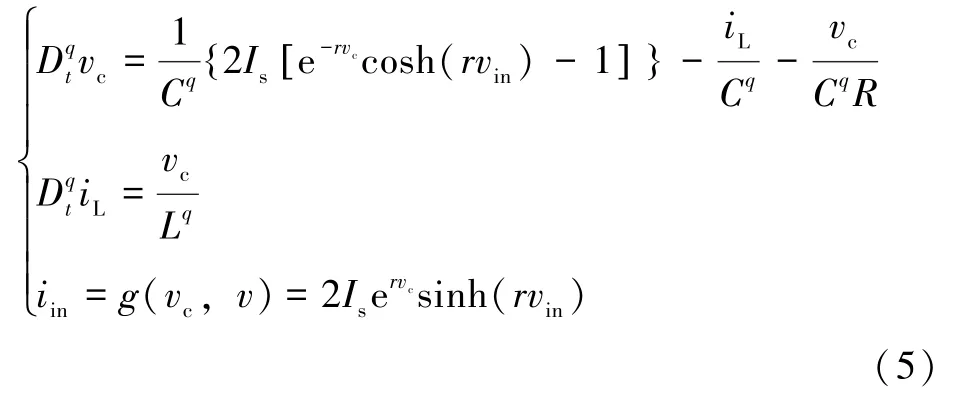
式中:r=1/(2nVT),其中n和VT分别表示二级管的发射系数和热电压;Is表示二极管的反向饱和电流;vin和iin分别表示二极管的输入电压和输入电流。本文将二极管参数设置为Is=2.682 nA,n=1.836,VT=25 mV。
根据上面建立的数学模型,通过Matlab 软件进行数值仿真,验证分数阶广义忆阻器的本质特征以及动态特性。这里给定一个正弦激励信号vin=Vmsin(2 πft),并将分数阶电容和电感设置为Lq=170 mH,Cq=4.7 nF,电阻值为R=1000 Ω。当输入信号的幅值为Vm=1.5 V,频率分别为500,1000 和2000 Hz 时,可以得到q=0.97 阶下忆阻器的紧磁滞回线,如图3(a)所示。从图3(a)可以看出,分数阶忆阻器上的电压电流关系轨迹图是通过原点收缩的回线,并且随着频率的增大,紧磁滞回线包围的面积将变小,当频率无穷大时,形成一条非线性的单值函数。同样地,为了验证分数阶次对忆阻器的影响,频率定为1000 Hz (其他参数不变),绘制出忆阻器在不同分数阶次下的紧磁滞回线,如图3(b)所示。不难发现,分数阶阶次对忆阻器的动态特性有一定的影响,并且在相同参数下,随着分数阶阶次的减小,紧磁滞回线包围的旁瓣面积会逐渐变大。
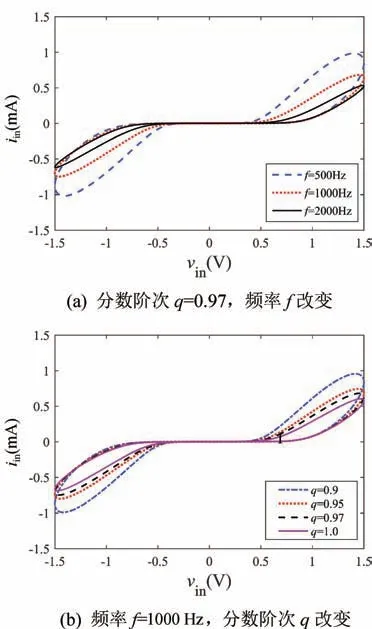
图3 分数阶广义忆阻器的紧磁滞回线Fig.3 Tight hysteresis loop of the fractional-order generalized memristor
1.3 分数阶忆阻混沌电路建模
本文采用分数阶广义忆阻器替换掉蔡氏振荡器中的蔡氏二极管,并且将蔡氏振荡器中的非线性元件用分数阶的电容和电感表示,组合成一种新型的分数阶忆阻混沌电路。分数阶电路等效模型如图4 所示。可以发现,该系统中包括七个电路元件,其中分数阶元件就有四个,它们分别是两个分数阶电容与、一个分数阶电感Lq和一个分数阶忆阻器Mq,其他元件为两个线性电阻和一个负电导。根据图4,可以写出分数阶忆阻混沌电路的数学模型如下:
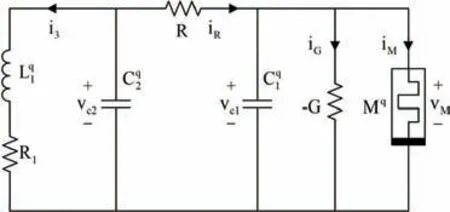
图4 分数阶广义忆阻混沌电路Fig.4 Fractional-order generalized memristor-based chaotic circuit
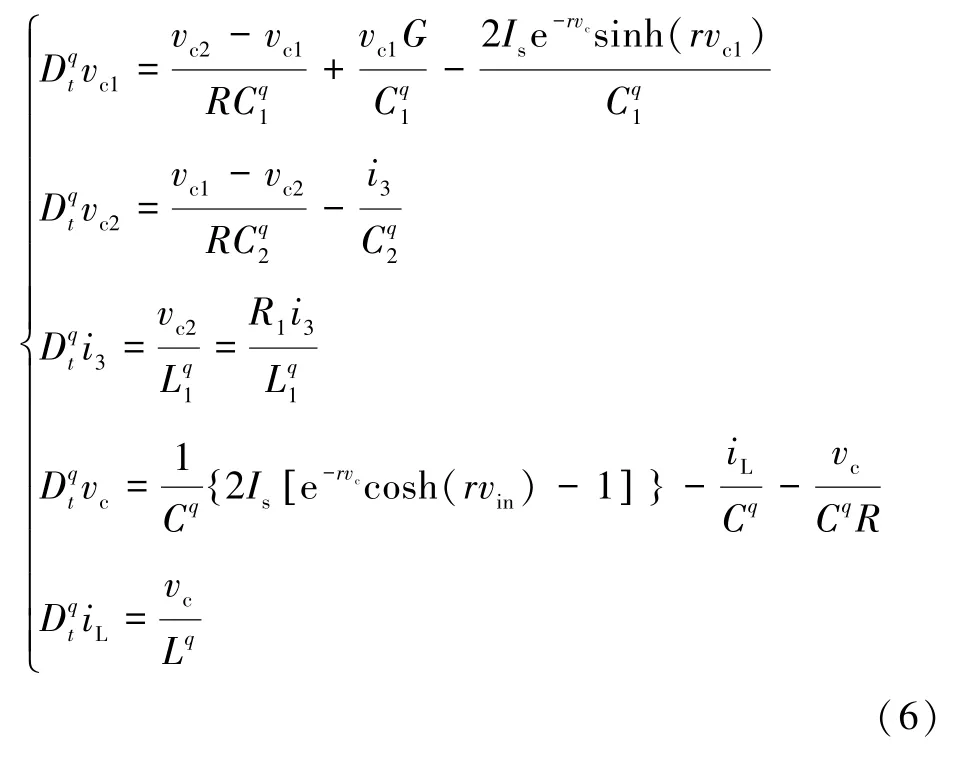
式中:vc1和vc2分别表示两个分数阶电容和上的电压;i3表示分数阶电感上的电流;vc表示忆阻器负载中的分数阶电容Cq上的电压;iL表示忆阻器负载中的分数阶电感Lq上的电流;R表示忆阻器的内阻。
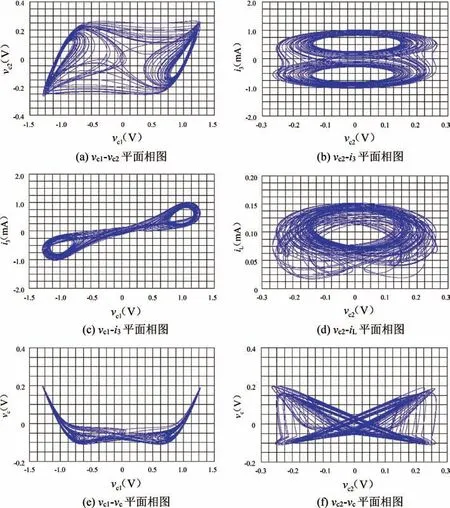
根据上面建立的数学模型,在MATLAB 软件中对模型进行数值仿真。将系统的参数值设置为电容=0.01 nF,电容=0.1 nF,电感=30 mH,电阻R1=2 Ω,电阻R=1800 Ω,电导G=0.6667 mS,分数阶广义忆阻器的参数保持不变。在系统初始值为(0.1,0.1,0,0,0)的情况下,通过求解系统在阶次q=0.97时的数值解,可以绘制出系统的相位图,如图5 所示。由相位图可以看出,分数阶系统的运动轨迹具有不确定性,表明系统处于混沌状态。
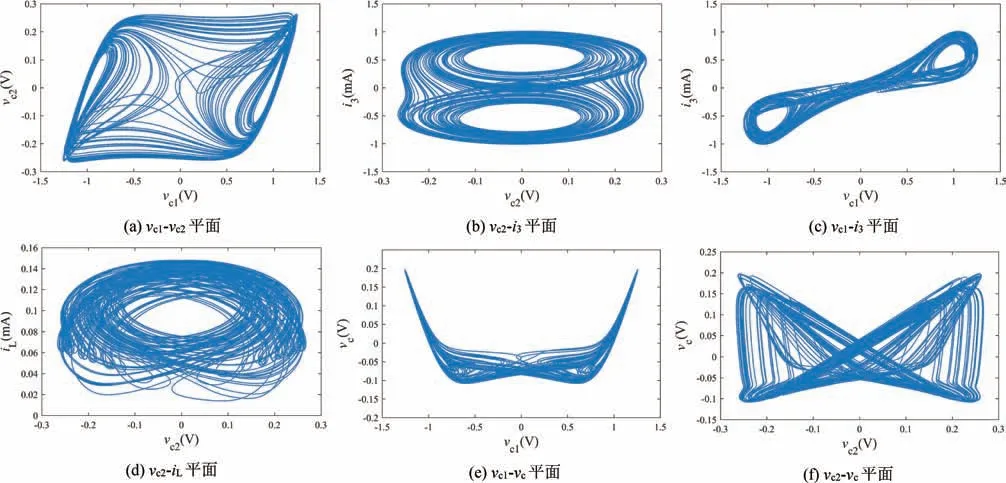
图5 分数阶忆阻混沌电路在不同平面上的相位图Fig.5 Phase diagrams of fractional-order memristor chaotic circuits on different planes
1.4 分数阶忆阻混沌电路建模
1.4.1 分数阶系统的稳定性
为了研究分数阶忆阻混沌电路的动力学行为,这里对系统的稳定性进行分析。首先求解系统的平衡点,将上面系统的方程公式(6)设置为0,通过整理简化后,则方程组变为如下的形式:
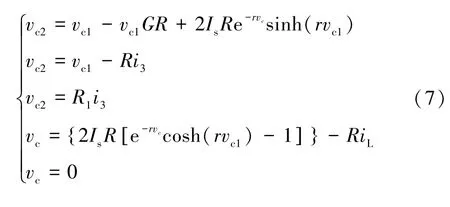
显然,分数阶忆阻混沌电路只有一个平衡点,即Q1=(0,0,0,0,0)。在Q1处的雅可比矩阵为:
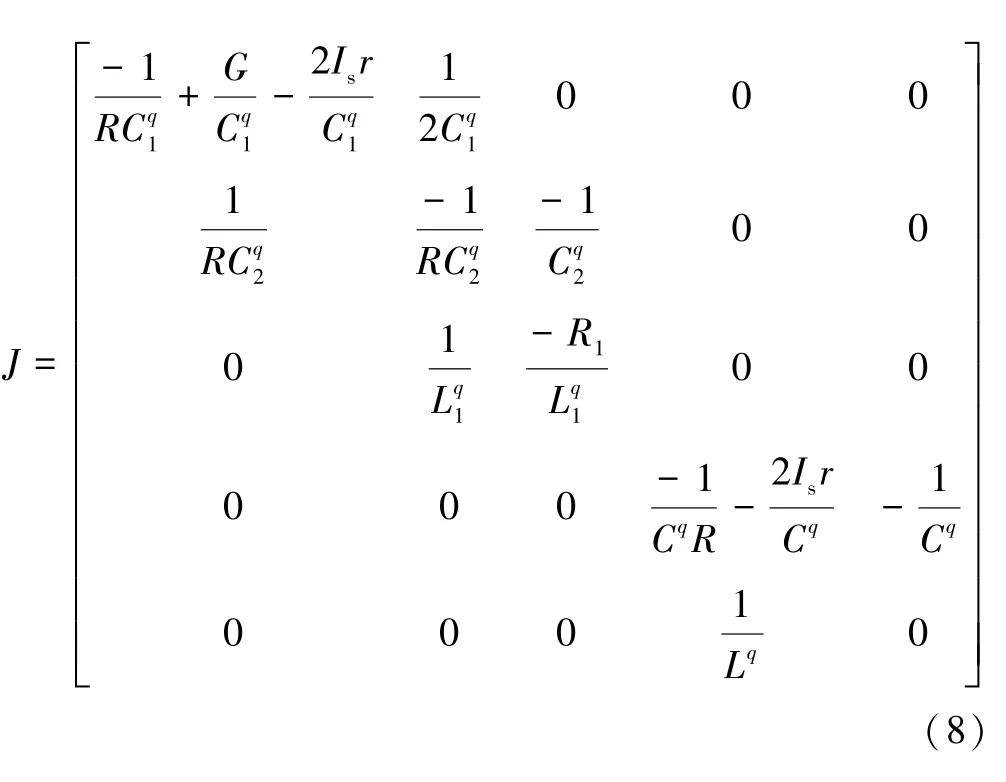
这里,通过对Jacobian 矩阵进一步处理,可以得到在平衡点Q1处的特征值为:

可以看出计算得到的特征值有一个正的实根,由分数阶系统的稳定性理论[22],可以判断该平衡点为指数为1 的不稳定的鞍点。
1.4.2 分数阶系统的动力学行为
为了研究忆阻器参数对分数阶忆阻混沌系统的动力学行为的影响,这里选择将忆阻器中的分数阶电感Lq的值作为变量,当系统的其他参数都不变,分数阶电感Lq的参数值从140 mH 增加到200 mH 时,可以得到系统的分岔图如图6 所示。
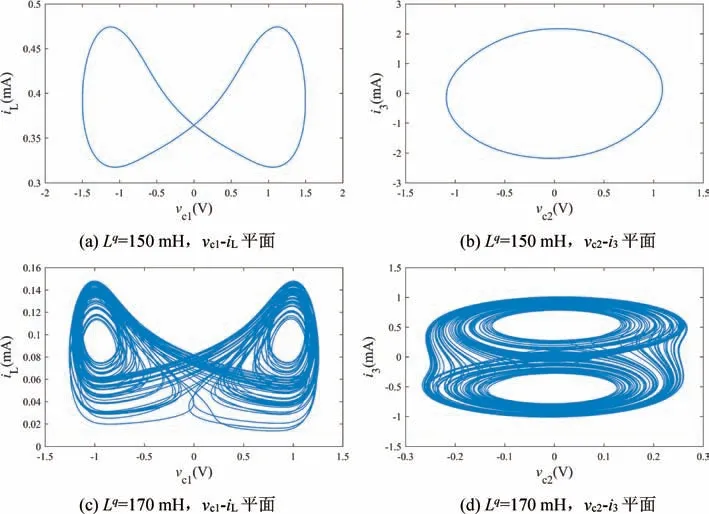
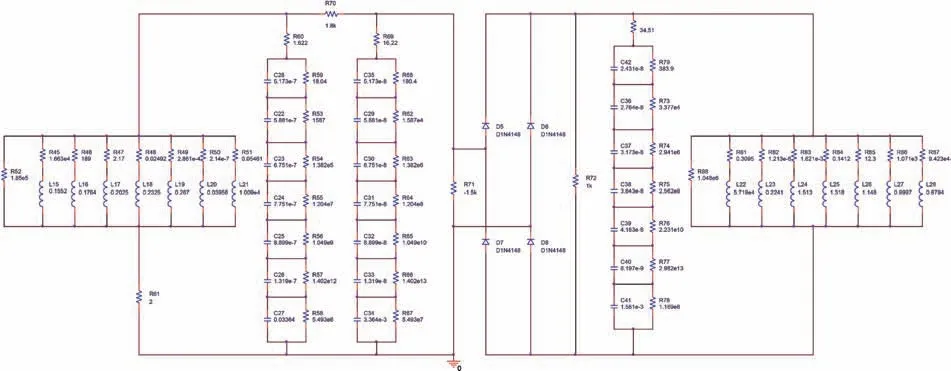
从图6 可以看出,随着参数值Lq的改变,系统可以表现出周期和混沌两种不同的状态。当分数阶电感的值的变化范围是140 mH 图6 分数阶电感Lq变化的分岔图Fig.6 Bifurcation diagram changed with fractional-order inductance Lq 图7 分数阶系统在不同电感Lq 时的相位图Fig.7 Phase diagrams of fractional-order systems changed with inductance Lq 为了实现分数阶广义忆阻混沌电路,需要建立分数阶电容和分数阶电感的等效电路模型。这里采用树型结构的分数阶模型来等效实现电容和电感,其实现原理主要是通过Oustaloup[23]滤波算法获得分数阶模块的传递函数,然后把传递函数化简为零极点的形式,并且通过电阻和电容或者电感进行串并联从而等效实现。分数阶电容和分数阶电感的实际等效电路如图8所示。 图8 分数阶电容和分数阶电感等效实现Fig.8 Equivalent realization of fractional-order capacitor and fractional-order inductor 通过图8 所示的分数阶等效电路模型,分别可以得到分数阶电容和分数阶电感的等效电路表达式: 在分数阶忆阻混沌电路中,根据式(10)和式(11)可以计算出分数阶电容和分数阶电感的具体参数值。当分数阶阶次q=0.97 时,通过计算可以得到分数阶电感Lq=170 mH,=30 mH 以及分数阶电容Cq=4.7 nF,=0.01 nF,=0.1 nF 的等效电路参数值,如表1~4 所示。 表1 q=0.97 时分数阶电容的等效电阻参数Tab.1 The equivalent resistance parameter of fractional capacitance at q=0.97 通过上一节对分数阶电容和分数阶电感建模,以及对分数阶忆阻混沌电路中的电容和电感的求解(具体的数值已列出),本节将通过PSpice 软件实现对分数阶广义忆阻混沌电路的仿真。在PSpice 软件中将分数阶电容和分数阶电感按图8 中的等效电路模型进行搭建。此外,电路中的二极管选择型号为IN4148 的二极管,并且将图4 中的负电导G用一个1500 Ω 的负电阻进行代替。在PSpice 软件中建立的分数阶等效电路模型如图9 所示,通过电路仿真,可以得到分数阶忆阻混沌电路的相位图如图10 所示。从仿真结果可以发现,分数阶电路仿真的结果与数值仿真的结果基本一致,从而验证了理论分析的正确性以及分数阶忆阻混沌电路的实用性。 图9 PSpice 中分数阶忆阻混沌电路模型Fig.9 Model of fractional-order memristor-based chaotic circuit in PSpice 图10 PSpice 电路仿真结果Fig.10 Circuit simulation results in PSpice 表2 q=0.97 时分数阶电容的等效电容参数Tab.2 The equivalent capacitance parameter of fractional capacitance at q=0.97 表3 q=0.97 时分数阶电感的等效电阻参数Tab.3 The equivalent resistance parameter of fractional inductor at q=0.97 表4 q=0.97 时分数阶电感的等效电感参数Tab.4 The equivalent inductor parameter of fractional inductor at q=0.97 忆阻器作为一种非线性器件,在混沌电路中的应用具有重要的意义。由于分数阶微积分对实际电路的描述更加准确,本文提出了一种新型的分数阶广义忆阻器。通过建立分数阶忆阻器的数学模型,并在Matlab 中进行数值仿真,对分数阶忆阻器的特性进行了验证分析。然后,结合蔡氏振荡器,构建了一种基于分数阶忆阻器的混沌电路,并将电路中的所有电容与电感推广到了分数阶次。通过改变分数阶混沌电路中的系统参数,并结合分岔图与相图等,对分数阶系统的动力学特性进行了分析。最后,建立了分数阶电容与电感的等效电路模型,并在PSpice 中建立了分数阶忆阻混沌电路的分数阶电路模型。通过电路仿真,得到相应的相图。电路仿真实验结果与数值仿真分析基本一致,表明了分数阶忆阻混沌电路的可实现性,对实际工程中的设计与应用具有重要的参考意义。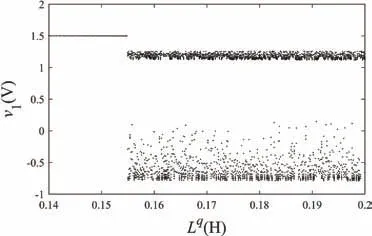
2 分数阶忆阻混沌电路的等效实现
2.1 分数阶电感电容的建模
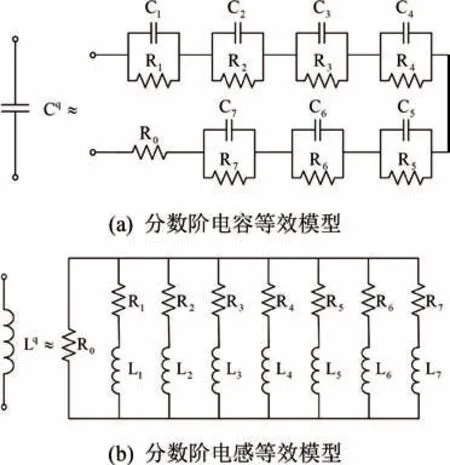
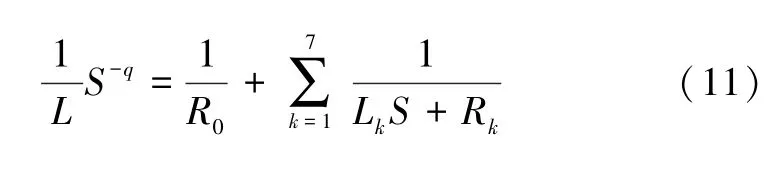

2.2 分数阶电路仿真



3 结论

