基于忆阻器的多路复用器设计与实现

姚 廉,刘 鹏,武继刚

(广东工业大学计算机学院,广州 510006)

传统的冯诺依曼体系结构中,存储器与处理器的分离导致大量时间和资源都浪费在数据传输过程．忆阻器[1]作为一种新型无源器件,由于其功耗低、集成度高和非易失性等特点而备受关注．忆阻器的阻值具有“开关效应”,故能用于数据存储,如作为突触权因子以实现神经网络的权值,并且不会因为断电而丢失数据[2]．目前,阈值电流模型(threshold adaptive memristor,TEAM)[3]、阈值电压模型(voltage threshold adaptive memristor,VTEAM)[4]及价离子变化模型(valence change memory,VCM)[5]等多种忆阻器模型被相继提出,其中VTEAM的应用最为广泛．在VTEAM模型中,当施加在忆阻器两端的电压超过正向阈值电压Voff时,忆阻器被置为高阻态Roff;当施加在忆阻器两端的电压超过负向阈值电压Von时,忆阻器被置为低阻态Ron;其他情况下,忆阻器的阻态不会发生变化．2010年,惠普实验室首次证明了忆阻器可以进行逻辑运算[6]．随后多种忆阻器逻辑被提出并用于设计复杂逻辑电路,其中最具有代表性的有忆阻器蕴含逻辑(material implication logic,IMPLY)[6]、忆阻器非蕴含逻辑(not-material implication logic,N-IMPLY)[7]和忆阻器辅助逻辑(memristor aided logic,MAGIC)[8]．尽管这些逻辑能够用于逻辑电路的设计,但是仅利用一种逻辑构建复杂逻辑电路的效率却较低,如为了实现4-1多路复用器,Karimi等[9]利用IMPLY逻辑时需要7个忆阻器和27个操作步骤;Wang等[10]利用N-IMPLY逻辑时需要12个忆阻器和15个操作步骤．本文拟结合IMPLY逻辑和N-IMPLY逻辑的功能特点,将2种逻辑同时应用到多路复用器的实现中,通过2种逻辑的迭代运算优化多路复用器的设计．

1 基于忆阻器的蕴含逻辑和非蕴含逻辑

1.1 忆阻器数学模型

忆阻器的等效模型如图1所示．该模型由2个铂(Pt)电极和电极中间夹杂的二氧化钛(TiO2)薄膜组成．二氧化钛薄膜分为纯TiO2绝缘层(未掺杂区)和氧空缺的TiO2-x层(掺杂区)2个部分,前者具有高电阻率,后者具有高电导率．忆阻器的电路符号如图2所示,掺杂区一端代表忆阻器的正极,非掺杂区一端代表忆阻器的负极．当负向电压施加在未掺杂区时,离子迁移使得氧空缺的TiO2-x层变宽,忆阻器的阻值会逐渐减小到低阻状态Ron．当正向电压施加在未掺杂区时,纯TiO2层变宽,忆阻器的阻值逐渐上升到高阻状态Roff．忆阻器的数学模型为

图1 忆阻器等效模型Fig.1 Equivalent model of memristor

图2 忆阻器符号Fig.2 Symbol of memristor

(1)

(2)

式中D为忆阻器的总长度,w为掺杂区的宽度,μ为离子平均迁移速率,V为施加在忆阻器两端的电压,I为通过忆阻器的电流,t为通电时间．

1.2 忆阻器蕴含逻辑(IMPLY)

IMPLY逻辑[6]的电路实现如图3所示,其中忆阻器P和忆阻器Q由一条水平纳米线相连,同时和一个接地的负载电阻RG串联．当在忆阻器的两端分别施加负值电压VC和负值电压VS,电路执行蕴含逻辑操作．执行完操作后,忆阻器P的阻值保持不变,忆阻器Q的阻值会根据2个忆阻器的前一阻值状态发生相应改变．IMPLY逻辑表达式描述如下:

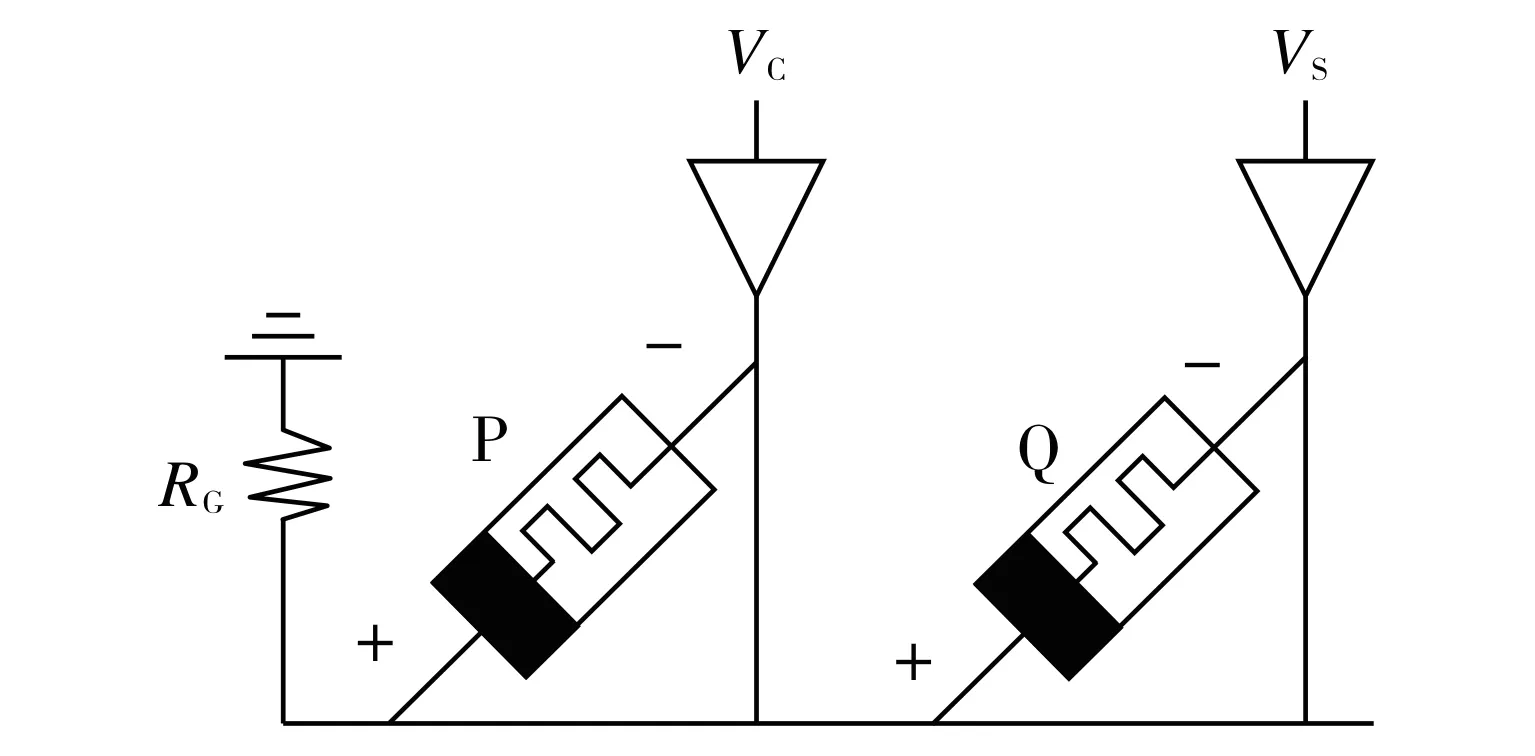
图3 IMPLY逻辑电路结构Fig.3 Circuit structure of IMPLY logic

(3)

式中p,q分别为忆阻器P和忆阻器Q的初始逻辑状态;q′为执行完逻辑操作后忆阻器Q的阻态,运算结果以阻值形式存储在忆阻器Q中;“→”表示IMPLY逻辑操作,真值如表1所示,其中逻辑“1”代表忆阻器处于低阻态,逻辑“0”代表忆阻器处于高阻态．

表1 IMPLY逻辑真值表Tab.1 Truth table of IMPLY logic

1.3 忆阻器非蕴含逻辑(N-IMPLY)

N-IMPLY逻辑与IMPLY逻辑的电路结构相似,如图4所示．施加在忆阻器两端的电压分别为一个负值电压VN和一个正值电压VP．N-IMPLY逻辑表达式描述如下:

图4 N-IMPLY逻辑电路结构Fig.4 Circuit structure of N-IMPLY logic

(4)

式中“⟹”表示N-IMPLY逻辑操作,其真值如表2所示．由逻辑表达式可见IMPLY逻辑自带“或”运算,N-IMPLY逻辑自带“与”运算．组合逻辑电路(如多路复用器)会包含多个“与”运算和“或”运算,仅利用IMPLY逻辑会导致实现“与”运算的步骤增加,而仅利用N-IMPLY逻辑会导致实现“或”运算的步骤增加;因此,本文考虑将IMPLY逻辑和N-IMPLY逻辑同时应用到多路复用器的设计中,通过降低计算深度达到减少操作步骤和忆阻器开销的目的．

表2 N-IMPLY逻辑真值表Tab.2 Truth table of N-IMPLY logic

2 多路复用器的实现

2.1 2-1多路复用器

2-1多路复用器的逻辑表达式如下:

(5)

式中O为输出结果,S0为选择信号,A0和A1分别代表2个待选择数据．当S0=0时,电路输出A0;当S0=1时,电路输出A1．为了减少实现该电路的操作步骤,尽可能地将式(5)中每一个子项转化为带有非的“或”运算或“与”运算．根据摩根定律,将式(5)转化为

(6)

图5 2-1多路复用器电路结构Fig.5 Circuit structure of 2-1 multiplexer

表3 2-1多路复用器实现步骤Tab.3 Operation steps for the implementation of 2-1 multiplexer

2.2 4-1多路复用器

随电路复杂性的增加,本文方法对电路时延和面积开销性能的优化更为明显．现利用所提出的电路设计方法,设计更为复杂的4-1多路复用器电路,其逻辑表达式如下:

(7)

式中S1,S2分别为选择位;A2,A3,A4,A5分别为4个待选择数据．当S1S2=00时,电路输出A2;当S1S2=01时,电路输出A3;当S1S2=10时,电路输出A4;当S1S2=11时,电路输出A5．对式(7)进行如下变换:

(8)

(9)

(10)

图6 4-1多路复用器的电路结构Fig.6 Circuit structure of 4-1 multiplexer

表4 4-1多路复用器实现步骤Tab.4 Operation steps for the implementation of 4-1 multiplexer

IMPLY逻辑和N-IMPLY逻辑均以第二忆阻器为输出忆阻器,而不影响第一忆阻器中的初始值,该特性将导致存储在第二忆阻器中的初始值不能在后续操作中被利用．现根据式(9)(10)调整逻辑操作的执行顺序,以尽可能多地复用忆阻器单元的初始值,进而在后续操作中减少额外的数据写入操作．例如,4-1多路复用器的实现中虽然步骤1和步骤3都利用了忆阻器M6的初始值,但是步骤3的IMPLY逻辑操作是将M6作为输出忆阻器,导致M6中的初始值S2不能用于后续逻辑操作,而步骤1则将M6作为第一输入忆阻器,其N-IMPLY逻辑操作不会破坏M6中的数据,故本文先执行M6⟹M1,后执行M3→M6．类似的情况还有步骤2和步骤6．本文所提方法由于最大程度地复用忆阻器单元初始值,在计算过程中无需额外的数据写入操作,故实现4-1多路复用器仅需7个忆阻器和9个操作步骤．

3 仿真结果与性能分析

通过仿真软件HSPICE对所设计的2-1和4-1多路复用器电路进行仿真实验,忆阻器模型采用VTEAM模型[1],忆阻器的仿真参数与文献[11]中真实器件铂-二氧化铪-氮化钛(Pt-HfO2-TiN)的实验数据相拟合．此处取Ron=5 kΩ,Roff=1 000 kΩ,Von=-1.3 V,Voff=1 V．执行2种逻辑所施加的电压取VS=-1.38 V,VC=-1.36 V,VN=-1.03 V,VP=1.06 V,kon=-8 000 m·s-1,koff=10-2m·s-1．负载电阻RG为500 Ω．

图7为2-1多路复用器中选择位S0=0时的仿真结果,待选择数据A0和A1分别为逻辑0和逻辑1,即M2和M3的初始状态分别为高阻态和低阻态．最后的输出结果以阻值形式保存在M2中．由图7可知,当S0=0时,忆阻器M2最后的阻值为高阻,即输出结果为逻辑0,与理论相符．

图7 2-1多路复用器的仿真结果Fig.7 Simulation results of 2-1 multiplexer

图8为4-1多路复用器的仿真结果,其中待选择数据A2、A4、A5为逻辑0,A3为逻辑1．由于选择组合的情况过多,现仅展示选择位“S1S2”为“01”的实验结果．由图8可知,输出忆阻器M2最后的阻值为低阻,即输出结果为逻辑1,与理论相符．

图8 4-1多路复用器的仿真结果Fig.8 Simulation results of 4-1 multiplexer

表5～6分别给出了本文所设计的2-1和4-1多路复用器与其他方法的对比结果．结果表明,本文方法所实现的2-1多路复用器及4-1多路复用器在忆阻器开销和操作步骤数目方面都优于其他方法．

表5 2-1多路复用器比较结果Tab.5 Comparisons with other approaches for 2-1 multiplexer

表6 4-1多路复用器比较结果Tab.6 Comparisons with other approaches for 4-1 multiplexer

4 结论

本文提出了同时使用忆阻器蕴含逻辑和忆阻器非蕴含逻辑实现2-1和4-1多路复用器的方法,通过分析2种忆阻逻辑的逻辑特性并设计相应的电路映射方案,对忆阻器开销和操作步骤同时进行了优化．利用本文方法所设计的2-1和4-1多路复用器仅需一个额外的辅助忆阻器即可实现相应的逻辑功能,电路面积开销大幅降低．仿真结果验证了该方法的可行性,且所提方法在时间延迟和面积开销性能方面均优于其他方法．