近群融合代数的不可约表示

俞立超,李立斌

(扬州大学数学科学学院,江苏 扬州 225002)

张量范畴是现今数学领域的一个重要研究方向,而融合范畴正是现今张量范畴研究的一个重要方向．Wasserman[1]确定了对称融合范畴的Drinfeld中心;董井成等[2]研究了秩为4的非平凡分次自对偶融合范畴,并对这个范畴上的Grothendieck环进行了分类;王志华等[3]讨论了融合环上的广义Cartan矩阵．自2003年Siehler[4]提出近群融合范畴的概念以来,国内外关于近群融合范畴已有许多研究成果．Evans等[5]讨论了近群融合范畴上的对偶;董井成等[6]刻画了近群融合范畴的结构,并对其进行了分类;苑呈涛等[7]给出了可范畴化的近群融合环K(Z3,3)上的所有不可分解Z+-模;Tucker[8]提出近群融合环上Frobenius-Schur指数的概念．若一个环具有Z+-基S,且对于任意g,h∈G,S中一个固定的元X满足以下融合规则:g·h=gh;g·X=X·g=X;X2=∑g∈Gg+nX,其中G为S中所有可逆元构成的有限群,n为给定的非负整数,则称该环为近群融合环,记为K(G,n)．本文主要计算近群融合环K(G,n)的Casimir数,并给出复数域C上近群融合代数A=K(G,n)⊗ZC上所有互不同构的不可约表示．

1 预备知识

引理1设G是一个群,(V,ρ)是群G的不可约非平凡表示,则有∑g∈Gρ(g)=0．

证明 若dimV=1．由于(V,ρ)是非平凡表示,则存在g0∈G,λ≠1使得ρ(g0)=λ．注意到(ρ(g0)-1)∑g∈Gρ(g)=∑g∈Gρ(g)-∑g∈Gρ(g)=0,且ρ(g0)-1=λ-1在复数域上存在逆元,故∑g∈Gρ(g)=0．

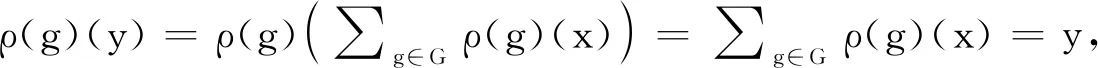
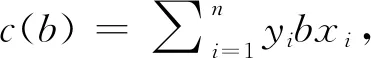
2 主要结果

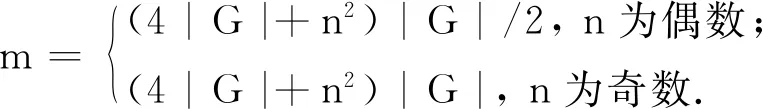
(1)

(2)

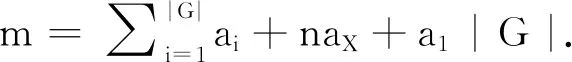
推论4K(G,n)⊗ZC是半单代数．

证明 根据定理3可得,K(G,n)⊗ZC的Casimir数不为0,因此由Higman定理[11]知,K(G,n)⊗ZC是半单代数．

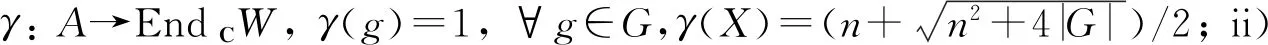
定理5上述构造出的(W,γ)是A的表示．

证明 根据上述构造方式,易验证(W,γ)一定是CG表示,所以为了判断(W,γ)是否是A的表示只须验证γ(Xg)=γ(X)γ(g)=γ(g)γ(X)=γ(X),∀g∈G;γ(X2)=γ(∑g∈Gg+nX)．

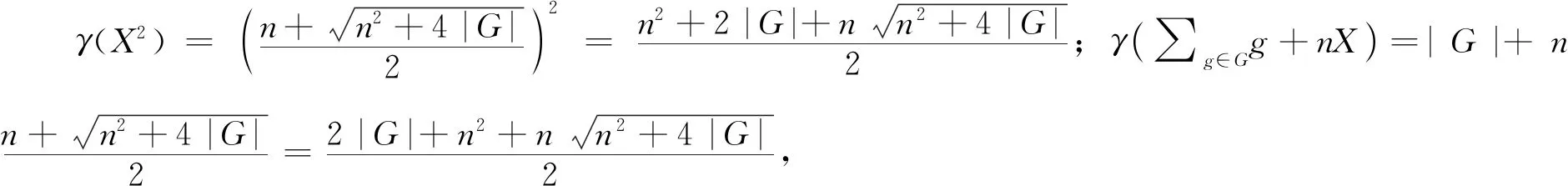
定理6设(V,ρ)是G的一个不可约表示,A=K(G,n)⊗ZC且(W,γ)是上述构造出的一个A的表示,则(W,γ)是A的不可约表示．

证明 若(W,γ)存在非平凡子表示(N,γ|N),则(N,γ|N)满足A作用封闭,即G作用封闭．由于(W,γ)可自然看作G的表示,从而作为G的表示,有(W,γ)=(V,ρ),即(N,γ|N)是(V,ρ)的子表示,这与(V,ρ)是G的不可约表示矛盾．

设{(V1,ρ1),(V2,ρ2),…,(Vs,ρs)}是CG上的互不同构的不可约表示,其中(V1,ρ1)是平凡表示．由(V1,ρ1)构造的2个A的不可约表示记作(W0,γ0)和(W1,γ1),由(Vi,ρi)(i≥2)构造的A的不可约表示记作(Wi,γi)．

定理7设A=K(G,n)⊗ZC且群G的互不同构表示为{(V1,ρ1),(V2,ρ2),…,(Vs,ρs)},则A的所有互不同构的不可约表示就是{(W0,γ0),(W1,γ1),(W2,γ2),…,(Ws,γs)}．