全驱动AUV动力定位系统滑模控制研究

谢争明,曾庆军,朱志宇,周启润,马洪潮

(江苏科技大学电子信息学院,江苏 镇江 212100)

自主水下机器人(autonomous underwater vehicle,AUV)动力定位控制是利用推进系统克服浪流等扰动,使AUV以指定姿态和位置保持在基准点或基准线附近[1]．随着海洋探索工具的发展和资源探索的深入,AUV工作愈复杂多样[2-3],包括水下悬停、定速巡航、航迹保持等,其控制要求也随之提高．全驱动AUV使用多个推进器提供推力,能够有效提升AUV的可操作性及抗干扰能力,确保更高的准确性及稳定性[4]．Liu等[5]设计了一种利用虚拟闭环系统提供虚拟参考轨迹的控制策略,解决了AUV跟踪控制的初始误差问题,但未进行湖上试验,对实际扰动考虑不足;Guerrero等[6]基于一组轨迹跟踪的饱和函数设计非线性PID控制器,在控制系统参数变化和洋流扰动影响下完成了深度和航向角控制试验,结果表明在目标航向角改变时,AUV控制曲线会产生较大超调量．AUV因设备条件限制,推进系统的输出常常受到约束．Rashidi等[7]将拉盖尔函数与预测控制结合,完成约束条件下的仿真试验,能大幅提高计算效率,但对于深度和航向角的跟踪存在一定的滞后性;Campos等[8]基于具有可变参数的饱和函数,设计了一种用于AUV定点校准及轨迹跟踪控制的非线性控制器,能够提高参数不确定系统的鲁棒性,但该控制器仅利用PD控制,未能实现积分环节,系统稳态性不佳．本文以“探海I型”AUV为研究对象,拟建立六自由度空间运动模型,分析AUV推进系统与随机浪流扰动模型,设计基于扩张状态观测器(extended state observer,ESO)的AUV动力定位滑模控制器(sliding mode control,SMC),结合AUV结构特点及推进器分配位置,将动力定位控制分为垂直面与水平面两部分,分别通过滑模控制器计算控制要求的推力与转矩,同时利用ESO对AUV系统模型偏差和浪流等干扰进行补偿,以期AUV能够根据指定作业需求动态保持在某一位置或轨迹．

1 全驱动AUV运动模型

图1为“探海I型”AUV实体样机,其外形采用鱼雷设计,AUV的横向与纵向各有2个辅助推进器,负责控制AUV姿态;机器人艉部装载1个主推,用来提供AUV前进的推力,可通过调节艉部X型舵的角度以平衡附加转矩[9]．AUV须多次调试以提高控制系统在实际运行中的稳定性,考虑到试验成本较高,可通过仿真测试控制器及算法的可行性,从而提高试验效率并降低成本[10],本文通过Fluent软件辨识仿真试验中的水动力参数．

图1 “探海I型”AUVFig.1 “T-SEA I”AUV

图2为设计AUV仿真及运动模型时建立的两个坐标系,O0x0y0z0为大地坐标系,Oxyz为AUV运动坐标系．其中φ,θ,ψ分别为横倾角、纵倾角、航向角;X,Y,Z分别为AUV在x,y,z轴的合力[11];K,M,N分别为AUV围绕x,y,z轴的合力矩;u,v,w分别为前进速度、横向速度、垂向速度;p,q,r分别为横倾角速度、纵倾角速度、航向角速度[12]．

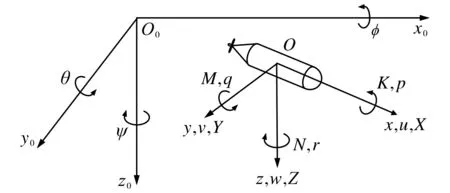
图2 坐标系Fig.2 Coordinate system

“探海I型”AUV简化运动模型为

(1)

式中m为AUV质量;Ix,Iy,Iz为转动惯量;xg,yg,zg分别为x,y,z轴重心坐标．AUV受到的合力和合力矩的矩阵为

F=[X,Y,Z,K,M,N]T=FHS+FH+Fprop,

(2)

其中FHS为AUV受到回复力和力矩的矩阵;Fprop为AUV受到推力和力矩的矩阵;FH为AUV受到水动力和力矩的矩阵．水动力影响大小通常与运动的速度和加速度有关[13],可表示为FH=[XH,YH,ZH,KH,MH,NH]T,式中XH,YH,ZH分别为x,y,z轴方向的水动力;KH,MH,NH分别为水动力围绕x,y,z轴作用的力矩．回复力为重力及浮力对AUV的作用,依照实际参数化简为

(3)

式中W为重力;B为浮力;xb,yb,zb为浮心坐标．

在对AUV进行运动分析时,应计算AUV与流体的相对速度,计算公式为

(4)

式中uA,vA,wA为相对速度;uc,vc,wc为运动坐标系下的水流速度．设定水流干扰为零均值水流干扰,若水流包含初始速度V0和水流方向ψ0,则

(5)

式中Vc为水流速度,ψc为水流方向,ω为高斯白噪声,μ1,μ2为非负常数．利用坐标变换矩阵Rn计算运动坐标系下水流

(6)

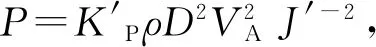
(7)

式中Xprop,Yprop,Zprop分别为x,y,z轴方向的推力;Kprop,Mprop,Nprop分别为推力围绕x,y,z轴作用的力矩;P1为主推进器推力,P2和P5为侧向推进器推力,P3和P4为垂向推进器推力;L2,L3,L4,L5为推力的力臂;Q1,Q2,Q3,Q4,Q5为转矩．

2 基于ESO的AUV动力定位滑模控制

本文将AUV运动分解为垂直面与水平面的运动,并将式(1)化简为垂直面和水平面方程

(8)

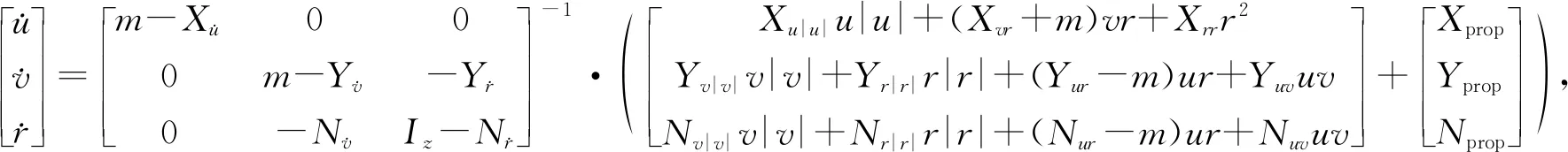
(9)

2.1 扩张状态观测器设计

将式(8)和式(9)化简为

(10)

式中f1(w,q,u),f2(w,q,θ,u),f3(u,v,r)为非线性函数;Bi为控制增益;Ut,i为控制量．将状态量w,q,u,v,r,θ,ζ扩张成二阶形式

(11)

式中Z1为状态估计量;Z2为扩张状态;h1,h2为增益矢量;e1为状态误差;α为常数矩阵;δ为滤波因子矩阵;fal(e1,α,δ)为函数滤波器[14],能够较好处理AUV等非线性系统的噪声干扰问题．

2.2 滑模控制器设计

将式(10)改写为

(12)

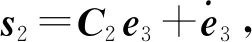
(13)

(14)

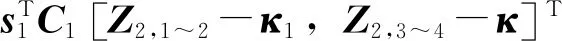
3 AUV动力定位仿真

为验证本文设计的控制器对动力定位的控制效果,在仿真中引入浪流等随机干扰,利用式(5)和式(6)计算干扰大小及方向．初始深度为0 m,设定目标深度8 m,目标航向角100°,目标横倾角及纵倾角为0°,在相同工况下设计动力定位试验,对比不同控制器的性能差异,仿真结果如图3和图4所示．由图3可知,引入随机浪流等扰动后,PID动力定位控制超调较大且易波动,在受到较大干扰时需要较长时间调整至期望状态;ESO滑模控制超调较小,能够在较短时间内调整至期望值并保持稳定．由图4可知,利用PID进行动力定位姿态角控制时收敛较慢,其中航向角在稳态时依然存在一定的误差;而ESO滑模控制在姿态角控制时,响应速度较快且能够较好地抑制扰动,快速平稳回到期望状态．

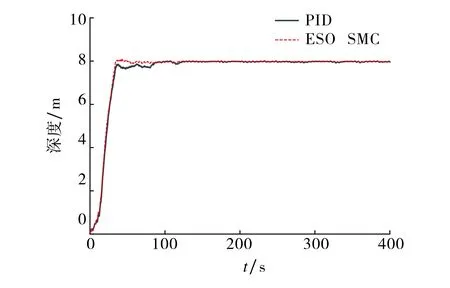
图3 深度控制对比图Fig.3 Comparison diagram of depth control

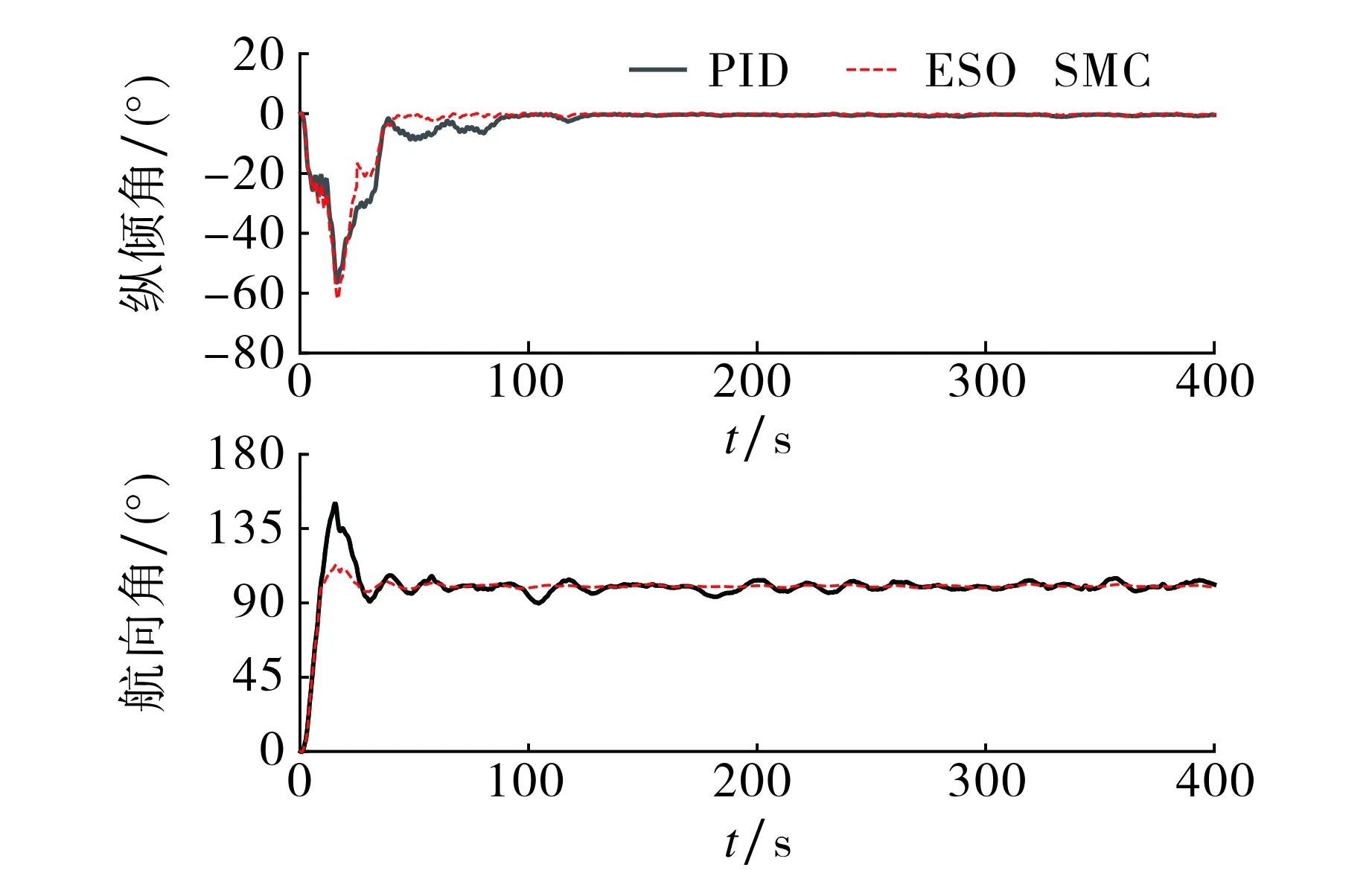
图4 动力定位姿态角控制对比图Fig.4 Comparison diagram of attitude angle control

4 湖上试验

AUV湖上试验于2020年2月在某湖完成,如图5所示．湖深5 m以上,水流速度小于2 m·s-1,水下环境较好,设计定深、定航动力定位控制任务:目标深度2 m,目标航向角200°,控制时长5 min．图6～8分别为AUV湖上试验的三维轨迹、深度及姿态角变化情况．由图6～8可知,设定任务后,AUV能够快速到达指定动力定位控制目标深度及航向,在100 s左右AUV航向角因扰动出现波动,但能够迅速回到稳定状态,并控制深度误差在±0.1 m以内,航向角误差在±2°以内,达到指定控制目标,能够应用在工程项目中．

图5 AUV湖上试验Fig.5 AUV experiments on the lake

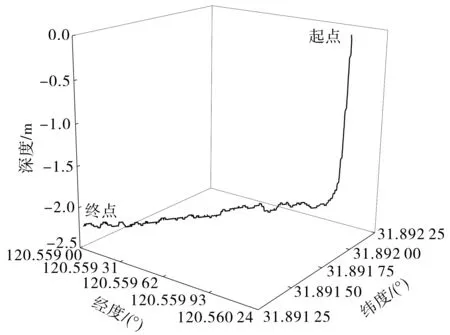
图6 动力定位三维轨迹Fig.6 3D trajectories for dynamic positioning

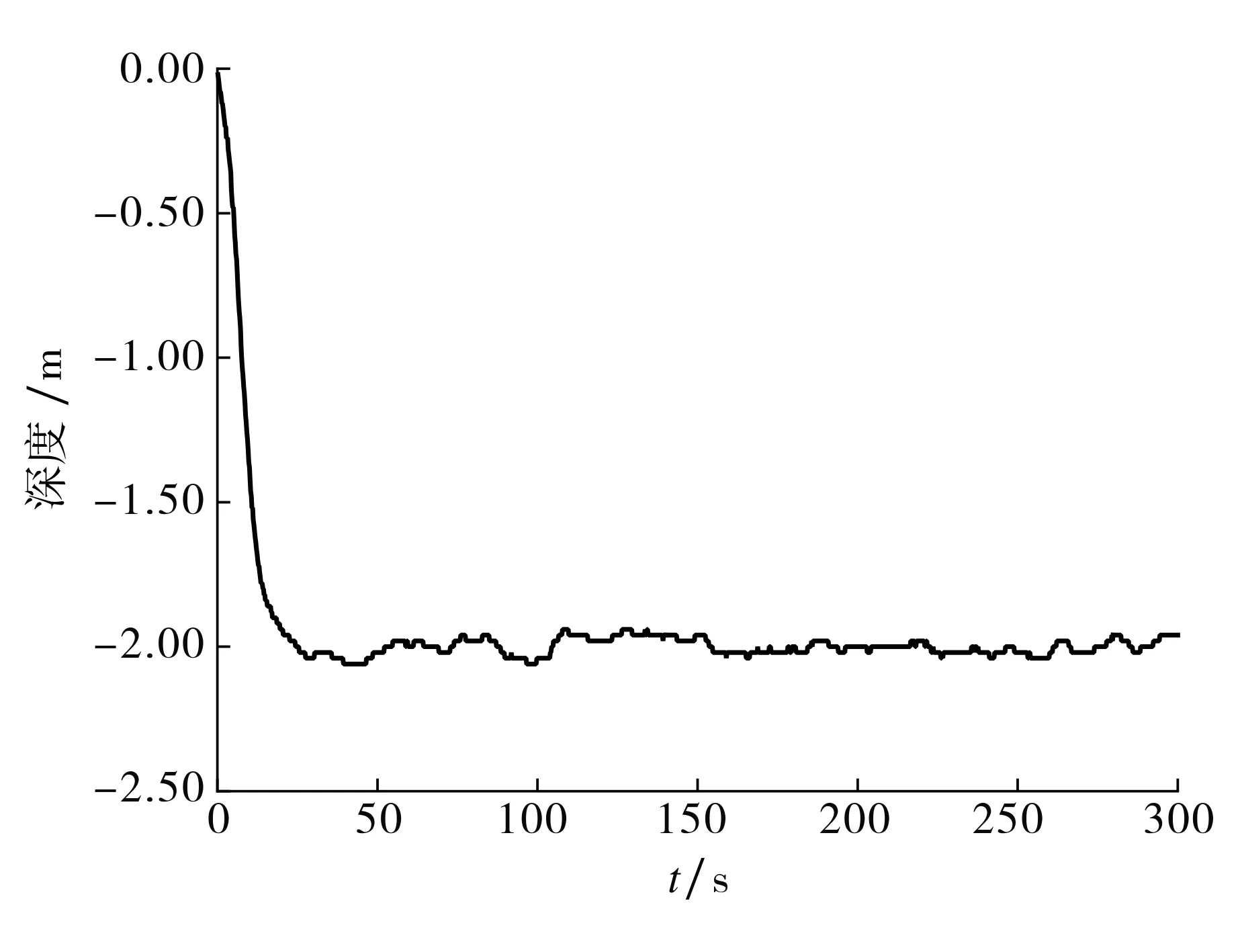
图7 深度控制Fig.7 Depth control

图8 姿态角控制Fig.8 Attitude Angle control