随动系统的新型非奇异快速终端滑模控制

史蒂芬 侯润民 顾晓辉 侯远龙

南京理工大学机械工程学院，南京，210094

0 引言

永磁交流伺服电机(permanent magnet synchronous motor，PMSM)具有响应快、效率高等优良性能，广泛应用于航天、船舶等工程应用领域[1-2]。某舰载武器位置控制伺服系统采用PMSM作为驱动电机，该控制系统中包含两个交流伺服电机，分别控制俯仰角和方位角。位置伺服系统在工作中存在齿轮间隙、摩擦力矩、海况扰动等干扰因素。这些扰动因素对该武器目标的跟踪精度及响应速度产生了较大影响，需要对扰动项进行估计并及时补偿[3]，以达到较为理想的控制效果。

在目标跟踪中存在脱靶量滞后等问题，为此吕明明等[4]设计了一种基于非线性跟踪微分器和统计模型的滞后补偿方法。针对跟踪微分过程中相位延迟问题，FENG等[5]应用泰勒公式进行补偿，抑制微分过程中的噪声。滑模控制具有较优良的鲁棒性，得到广泛研究及应用[6-7]。为了提升系统响应速度，XU等[8]提出了一种非奇异快速终端滑模(non-singular fast terminal sliding mode，NFTSM)控制方法，能在有限时间内快速收敛。SHAO 等[9]提出了一种自适应回归终端滑模控制方法，在递归结构中设计了非奇异快速终端滑模面和递归积分终端函数，能快速到达滑模面，使跟踪误差在有限时间内收敛到零，有效提高控制精度。非奇异快速终端滑模控制具有较强鲁棒性的前提是提高切换增益，然而较大的切换增益会引起系统抖振和稳态变化，因此，需要对扰动进行实时估计并补偿，避免切换增益过高。常用的方法有卡尔曼滤波补偿[10]、模型参考自适应法[11]、超螺旋扩张观测器法[12]等。

前馈人工神经网络(artificial neural network，ANN)能够有效逼近控制器，极大程度地简化计算过程，通过加载非线性负载验证动静态性能[13]。CHAOUI等[14]提出了一种自适应神经网络速度控制策略，该控制器的核心是径向基函数(RBF)网络，具有简单的模糊型结构以及较高的学习速率。滑模控制中的抖振现象会给机械元件带来磨损，降低控制精度，将滑模控制与自适应模糊、自适应神经网络相结合[15-16]，能够有效减小抖振。

本文基于泰勒公式，结合非线性函数fhan构造跟踪微分器，并对收敛时间进行分析计算，仿真结果证明基于泰勒公式的跟踪微分器(Taylor’s formula based tracking differentiator，TTD)能够有效抑制噪声，提升跟踪精度。将ARBF+TTD与RBF分别对扰动项估计，仿真结果证明ARBF与TTD结合的方法能够有效抑制微分峰值，精确度更高。运用MATLAB及半实物仿真平台进行正弦跟踪实验，验证了与NFTSM相比，NFTSM+ARBF控制算法动态跟踪性能得以提升，适用于该随动系统。

1 交流伺服电机数学模型

随动系统的总体结构如图1所示。首先应用旋转变压器测量电机轴的角位置，再应用轴角/数字转换模块得到相应的数字信号。通过计算机和数据采集卡完成系统的数据采集工作。控制计算机通过C++编程并传送控制律信号。得到的控制仿真量运用伺服放大器进行伺服放大及变换，将处理好的数据输入变频器，应用变频器控制交流伺服电机。

图1 舰载随动系统结构Fig.1 Structure of ship-borne servo system

该舰载随动系统的控制系统性能要求如下：①方向角范围为±101°；②俯仰角范围为-20°～55°；③动态跟踪误差为0.216°(均方根误差(RMSE)不得超过0.12°)。

系统负载较电机本身所引起的非线性更大，故可忽略电机本身产生的非线性。本文采用表贴式PMSM，在两相静止坐标系d-q轴上可求得数学模型：

(1)

其中，ud、uq分别为定子d-q轴的电压分量；id、iq为定子d-q轴的电流分量；Ld、Lq分别为定子d-q轴的电感分量；ψf为转子永磁体产生的磁链；R为定子电阻；p为电机极对数；J为转动惯量；B为摩擦因数；ω为转子角速度；Te为电磁转矩；Ke为转矩常数；TL为负载转矩。采用id=0控制方法，PMSM控制系统结构如图2所示。

图2 PMSM控制系统结构Fig.2 Structure of PMSM servo system

电机运行过程中存在参数摄动等扰动因素，式(1)中第3式可以表示成

(2)

定义

(3)

将式(3)代入(2)，可以得到

(4)

其中，d表示扰动项，包括电机摩擦扰动、海况扰动等外部扰动。

2 基于泰勒公式的微分跟踪器

韩京清等[17]提出的微分跟踪器的本质是通过构造跟踪速度的时间最优控制的动态系统来实现的，存在跟踪速度或快或慢。也就是说，相位延迟是不可避免的。在微分过程中存在噪声，由此有必要抑制噪声，并对相位延迟进行补偿，以提高跟踪精度。采用离散最速控制综合函数fhan构成的跟踪微分器为[18]

(5)

d=hr2a0=hω(k)y=θ(k)+a0

a2=a0+sgn(a1-d)/2

sy=(sgn(y+d)-sgn(y-d))/2

a=(a0+y-a2)sy+a2

sa=(sgn(a+d)-sgn(a-d))/2

(6)

式中，h为采样周期；r为待调整参数。

泰勒公式能够有效补偿相位延迟，提升微分跟踪器性能，泰勒公式为

(7)

假设跟踪信号为θ*，时间间隔为Δt，二阶跟踪微分器为

(8)

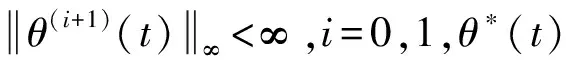
(9)

t∈[a，+∞)

证明：对式(9)求i阶导，可以得到

(10)

应用泰勒公式展开θ(i)(t)，可以得到

(11)

ξ∈(t，t+Δt)

式(12)减去式(11)的绝对值为

(12)

对式(13)进行拉普拉斯变换，可以得到

(13)

式(13)可简化为

(14)

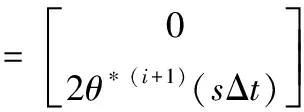
式(14)的解为

(15)

(16)

(17)

(18)

3 非奇异快速终端滑模控制

合并为整体扰动项f后，交流伺服电机的数学模型可以表示为

(19)

(20)

终端滑模(terminal sliding mode，TSM)与非奇异终端滑模(nonsingular terminal sliding mode，NTSM)表达式分别为

(21)

根据文献[20]，可计算出TSM和NTSM的收敛时间分别为

s=x1+α|x1|γ1sgn(x1)+β|x2|γ2sgn(x2)

(22)

α>0β>0 1<γ2<2γ1>γ2

收敛时间为

(23)

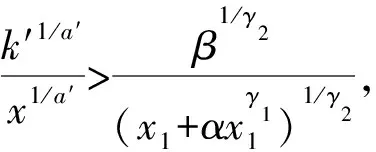
(24)

由上文证明，与FTSM相比，NFTSM具有更快的收敛速度。

4 基于ARBF的非奇异快速滑模控制

(25)

α>0β>0 1<γ2<2γ1>γ2

为了使式(20)能够快速到达滑模面，设计控制律如下：

(26)

ieq=1+αγ1|e|γ1-1sgn(e)

(27)

ib=K1sgn(s)+K2s

(28)

对式(25)求导，得

(29)

(30)

由上可得

(31)

则有

(32)

(33)

对式(33)求导，可以得到

(34)

图3 PMSM控制系统结构Fig.3 Structure of PMSM servo system

5 仿真验证

5.1 MATLAB仿真

根据所设计的控制器搭建PMSM仿真模型，运用MATLAB/Simulink中的S_function模块对自适应RBF非奇异滑模控制进行仿真。首先，应用式(6)所设计的微分跟踪器进行微分跟踪，参考信号为y=6sin(0.8t)，如图4、图5所示。

图4 跟踪微分器跟踪曲线Fig.4 Tracking curve of tracking differentiator

图5 基于泰勒公式的微分跟踪器跟踪曲线Fig.5 Tracking curve of TTD

由图4可知，跟踪微分器能够有效抑制微分过程中的噪声，但是存在相位延迟问题。由图5可知，TTD能够有效提高跟踪精度。

应用NFTSM控制器跟踪正弦曲线，设定该正弦曲线周期为3.768 s，幅值为±30°。分别应用NFTSM和NFTSM+ARBF+TTD两种控制方法进行目标跟踪实验。跟踪曲线以及跟踪误差如图6所示。

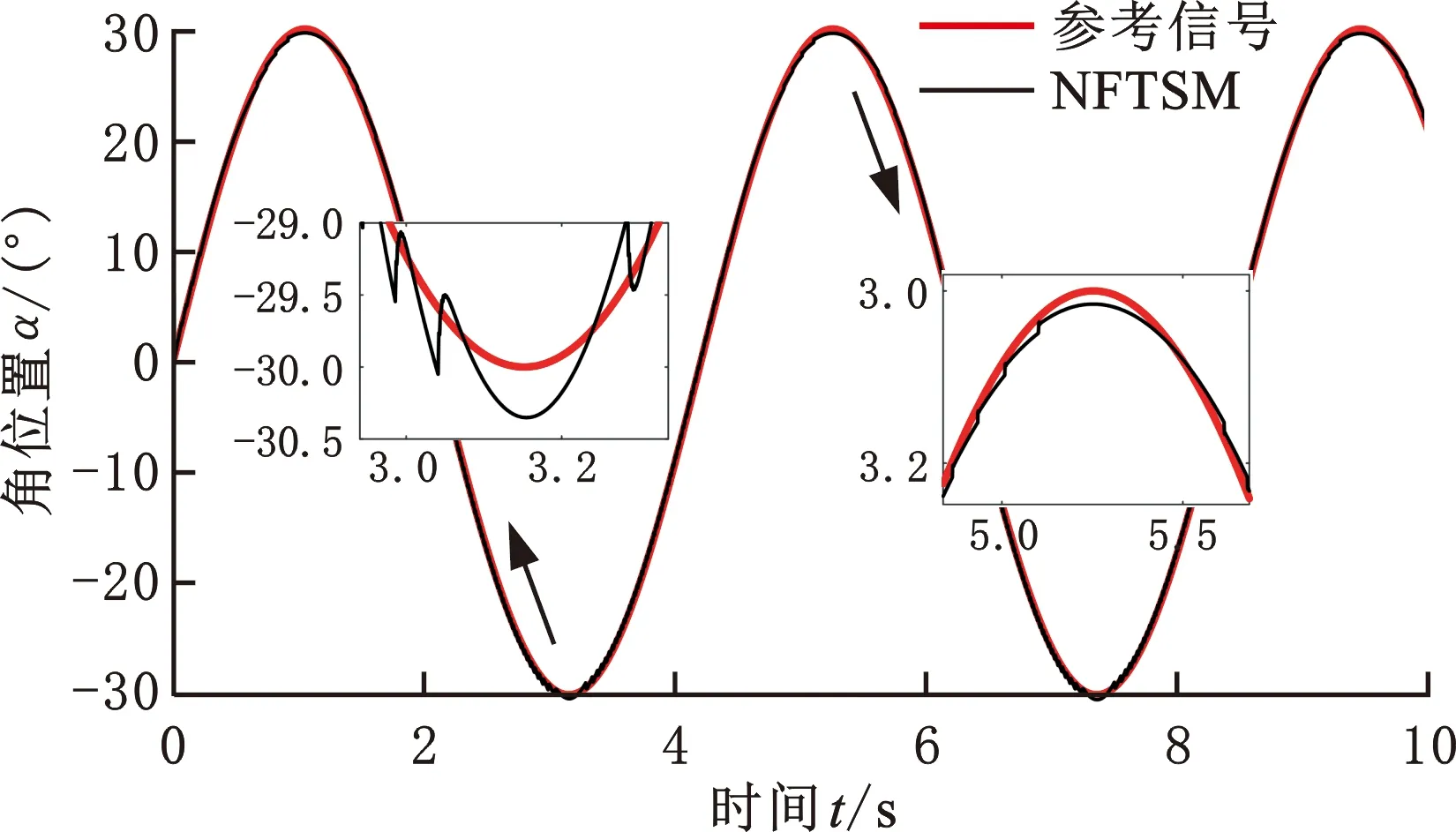
(a)跟踪曲线

(b)误差曲线图6 NFTSM正弦跟踪曲线Fig.6 Sinusoidal tracking by NFTSM

从图6可以看出，NFTSM在曲线顶端存在明显抖振。将ARBF和基于泰勒公式的TTD与NFTSM相结合，跟踪曲线如图7a所示，抖振得到极大改善。根据误差曲线，NFTSM最大误差为0.4885°，而NFTSM+ARBF+TTD跟踪曲线的最大误差为0.1219°，跟踪精度提升了3.98倍，鲁棒性更强。根据图7b，NFTSM+ARBF+TTD误差曲线较为光滑，抖振问题得到有效解决。

分别应用神经网络、ARBF对电机工作中的扰动f逼近，扰动估计如图8所示。红色曲线表示RBF对扰动项进行估计，可以看到在前0.2 s存在微分峰值现象。这说明应用ARBF+TTD能够有效抑制微分峰值问题，从而提高观测精度。

5.2 半实物仿真

(a)跟踪曲线

(b)误差曲线图7 NFTSM+ARBF+TTD正弦跟踪曲线Fig.7 Sinusoidal tracking by NFTSM+ARBF+TTD

图8 ARBF+TTD扰动估计Fig.8 Disturbance estimation by ARBF+TTD

应用实验室半实物仿真平台进行仿真验证。半实物仿真平台结构图及照片见图9。首先由控制计算机将控制目标传输给伺服控制系统，由控制系统驱动电机运转，应用可变转速比减速箱实现在负载前提下的调转。传感器采集角度数据，并传输给控制计算机，从而形成闭环结构。包括摩擦力矩、转动惯量等外部扰动，应用磁粉制动器模拟加载。将传感器得到的参数传递给控制计算机，从而实现较高精度的位置环控制。

图9 半实物仿真平台结构Fig.9 The semi-physical simulation platform structure

半实物仿真平台中的转动惯量盘和磁粉制动器为加载模块，模拟转动惯量和摩擦力矩。实际工程实践中的阻力力矩应用磁粉制动器进行模拟。交流伺服电机参数见表1。

减速箱采用模数为0.75的齿轮构成，需要确保减速器在工作时传动间隙不超过0.03°。最大负载力矩约为11 N·m。 转动惯量盘为可变模拟转动惯量装置，最大值为30 kg·m·s2。磁粉制动器模拟摩擦力矩为20 N·m。

图9中的可变转速比减速箱的结构如图10所示。它通过在各级齿轮的转动来达到降速的传动目的。电机传动作为输入轴，带动齿数少的齿轮转动，依次带动齿数多的齿轮运动，通过啮合传动达到减速的效果。同一个轴上安装有不同大小的齿轮，调整相邻不同齿轮啮合，即可得到不同减速比的传动。本文采用810∶1的传动比。动力减速箱依靠一对齿轮啮合运动，完成减速任务，其传动比为3∶1。

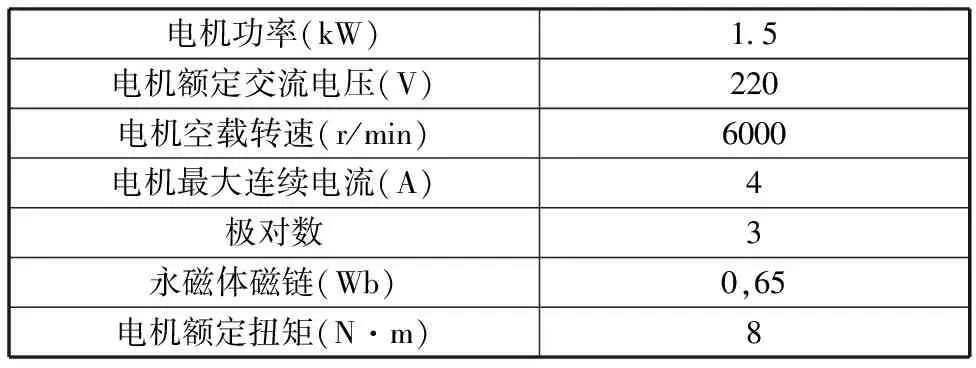
表1 交流伺服电机参数Tab.1 Parameters of the PMSM

图10 可变转速比减速箱Fig.10 Variable speed ratio gearbox

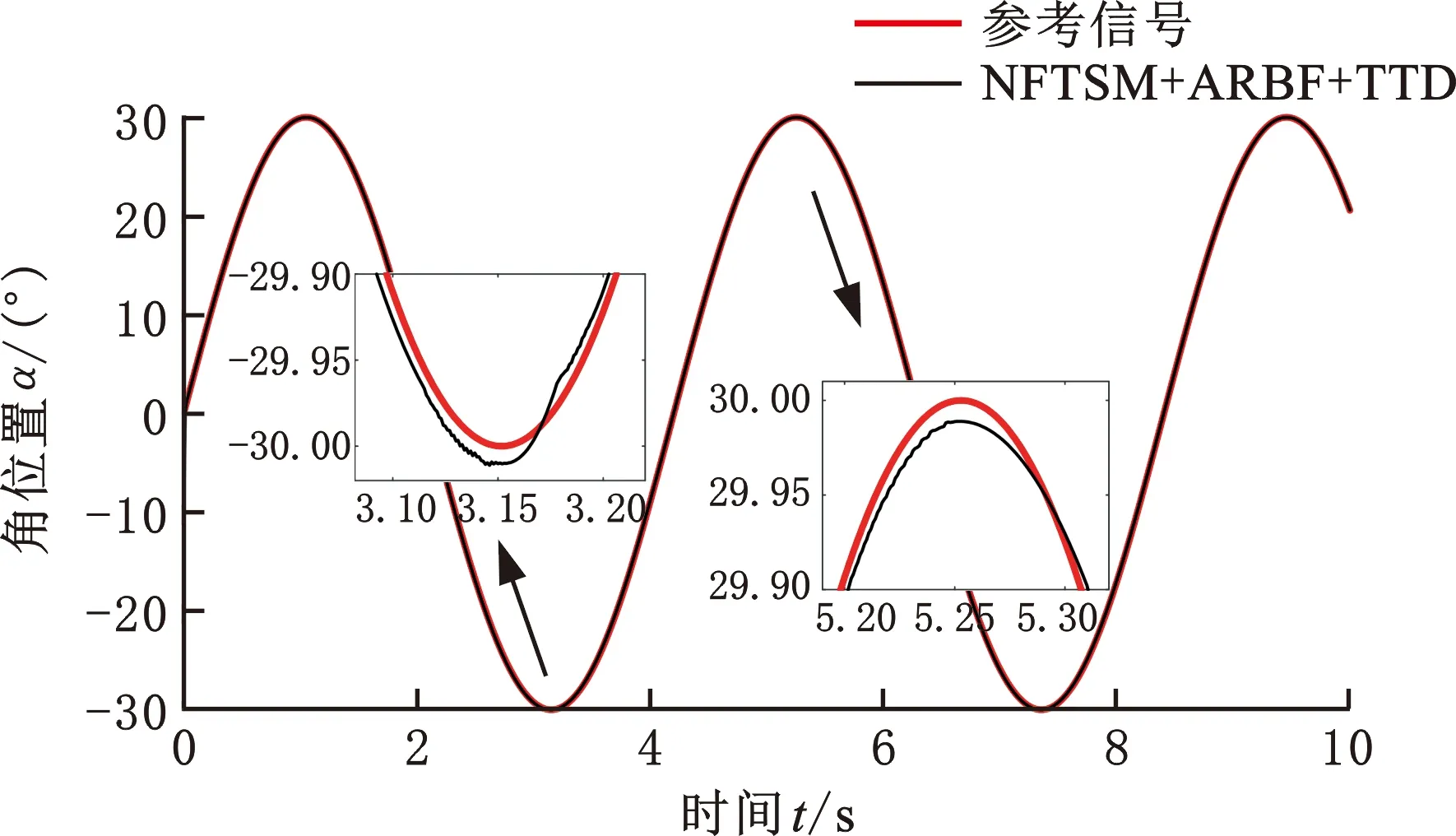
分别应用NFTSM和NFTSM+ARBF+TTD两种控制器跟踪幅值为±30°、周期为4.2 s的正弦信号。跟踪曲线如图11所示，在前3.5 s内跟踪误差较大，蓝色曲线更接近参考信号。跟踪误差如图12所示，前 3.5 s之后趋于稳定，NFTSM跟踪误差最大值约为0.2373°，RMSE值为0.0975，平均误差为0.0623°。NFTSM+ARBF+TTD控制策略的跟踪误差最大值为0.1404°，RMSE值为0.0735，平均误差为0.0318°。与NFTSM相比，误差相对较小，满足动态跟踪精度要求。因此，应进一步对半实物仿真平台及控制策略进行优化。

图11 半实物仿真正弦跟踪曲线Fig.11 Sinusoidal tracking curve by semi-physical simulation

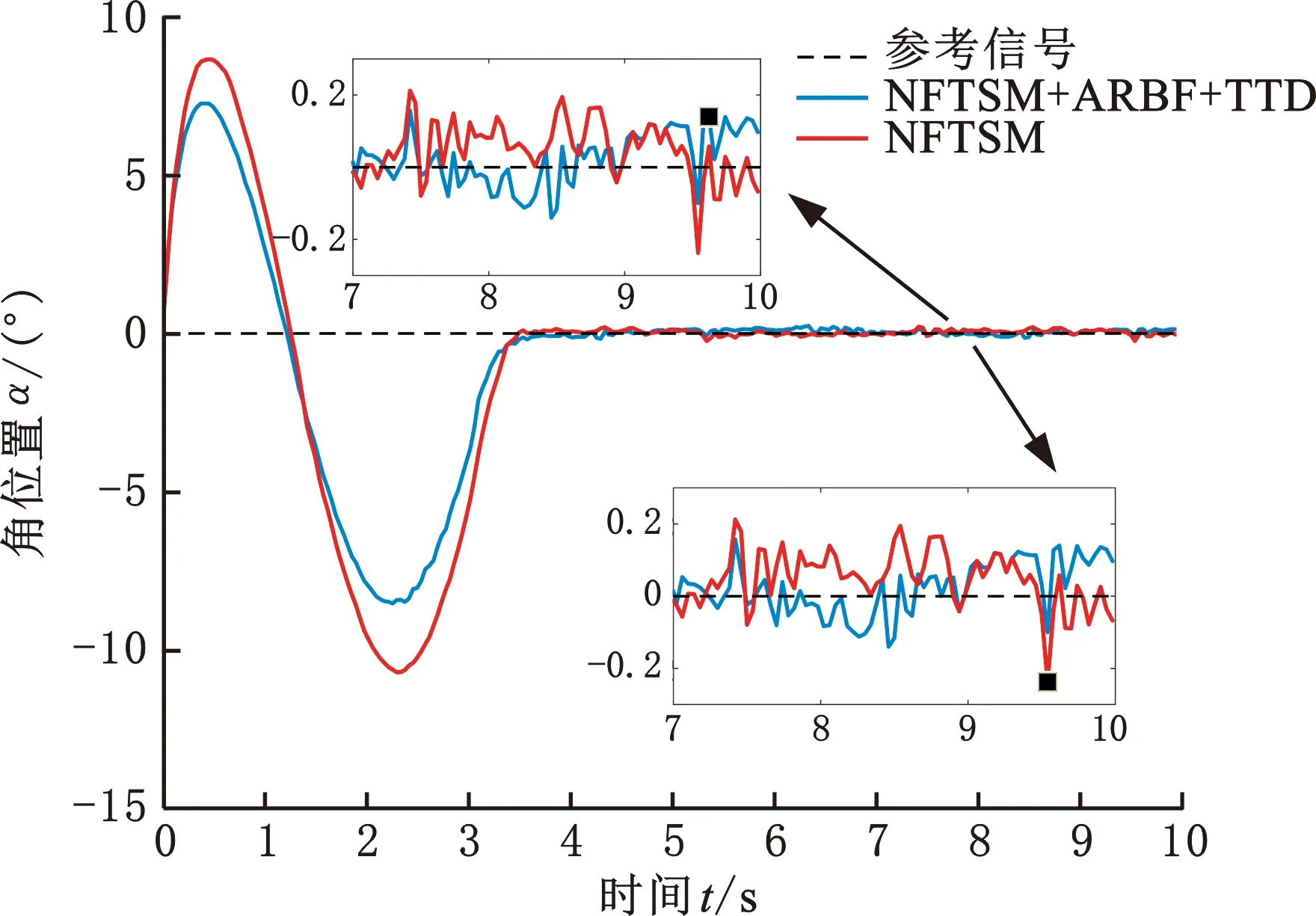
图12 半实物仿真正弦跟踪误差Fig.12 Sinusoidal tracking error by semi-physical simulation

6 结语

(1)本文设计了基于泰勒公式的跟踪微分器，仿真结果证明跟踪微分器能够有效抑制微分过程中产生的噪声。基于泰勒公式的跟踪微分器与传统跟踪微分器相比，相位延迟问题得到有效解决。

(2)应用MATLAB实现正弦跟踪仿真实验。实验结果表明，对于扰动估计后的NFTSM，应用ARBF+TTD能够有效抑制NFTSM控制中的抖振现象，跟踪精度得到提升。同时，与RBF相比，应用ARBF+TTD使扰动项估计和微分峰值问题得以有效抑制。

(3)应用半实物仿真平台进行正弦跟踪实验，实验结果表明，NFTSM+ARBF+TTD的跟踪性能优于NFTSM控制，这证明基于ARBF+TTD的非奇异滑模控制策略可有效提升系统动态跟踪性能，适用于舰载位置控制伺服系统。