中考微专题复习课的设计与思考
——以“隐圆问题”为例
江苏省苏州工业园区星海实验中学 (215000) 张 哲
“圆”是初中数学内容中较难的一个章节,和圆有关的问题中难度较大的要属“隐圆”问题了.近年各地中考试题中,“隐圆”问题出现的频率较高,其中常常涉及动点求线段最值问题.笔者认为在中考的复习中,可以采取微专题的模式,让学生对该类题型的思想方法、解题思路有更深层次的认识.
1. 微专题复习教学过程
1.1 根据圆的定义构造圆
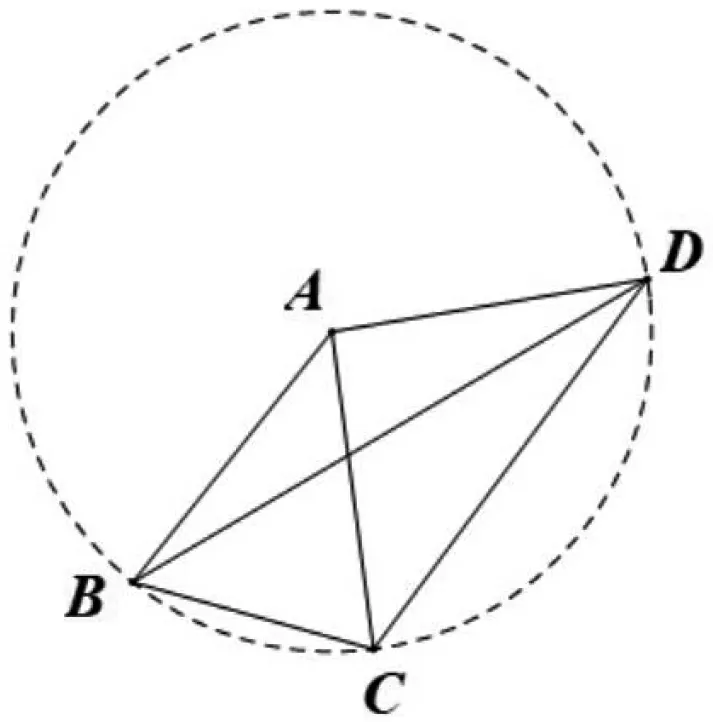
图1
例1 如图1,AB=AC=AD,∠CBD=2∠BDC,∠BAC=46°,则∠CAD
=________.

点评:在解决几何问题时,应结合已知条件,观察图形,联想条件相关的知识点.本题的条件AB=AC=AD,它们有一个公共顶点A,我们称之为“伞型”,由它联想到“到定点的距离等于定长”的圆的定义,从而画出对应的隐圆,将角度问题转化到圆内成为圆周角、圆心角问题去解决.
设计意图:由简单的题目切入,让学生从自己会做的题目入手,增强学生的自信心,提高学生学习的积极性和主动性.

图2
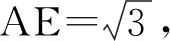

点评:本题以矩形的翻折为背景,研究最值问题.题中并未直接给出“伞型”条件,但是翻折问题里有很多隐含条件,包括对应线段相等、对应角度相等.本题由翻折得到BE=BG,继而想到“到定点的距离等于定长”,画出隐圆.本题有两个难点:一是将四边形面积的最值问题转化为三角形面积的最值问题,再进一步将三角形面积的最值问题转化为动点到定线段的距离问题;二是寻找动点轨迹.
图3
设计意图:与例1的隐圆构造方法一样,难度比例1大.在完成例1的基础上思考例2,提升学生的思维深度,对“利用定义构造圆”的方法进行巩固
1.2 根据定边对直角构造圆
例3 如图3,在RtΔABC中,AB⊥BC,AB=6,BC=4,P是ΔABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为________.
点评:本题由已知条件可得P点处是直角,而直角所对的边AD为定边,想到圆内的“直径对直角,直角对直径”,进而画出隐圆,得出P点的轨迹,将问题转化为求圆外一点到圆周上一点的最短距离.
设计意图:本题是“直角对直径”构造圆中较为典型的题型,难度不大,大部分学生应该可以独立解决.由典型题型切入,引导学生自己总结方法.

图4
例4 如图4,在等腰直角三角形ABC中,AB=AC=2,D是边AC上一个动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长的最小值
为________.
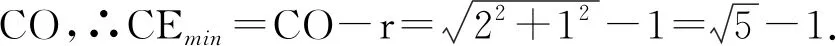
点评:本题动点E处是直角,不难想到“直角对直径”,存在隐圆.但是因本题中本身有一个圆,学生容易被这个已知圆干扰,错认为E的轨迹是以AD为直径的圆,从而错解.实际上因为D是动点,所以AD是动线段,因此这个已知圆也是不确定的.而∠AED的邻补角∠AEB也等于90°,且∠AEB的所对边AB是一条定边,因此E点的轨迹应该是以AB为直径的圆,画出隐圆后,问题迎刃而解.
设计意图:与例3是同类型的题型,在例3的基础上再进一步突破难点,加深学生对模型的理解.
1.3 根据定边对定角构造圆
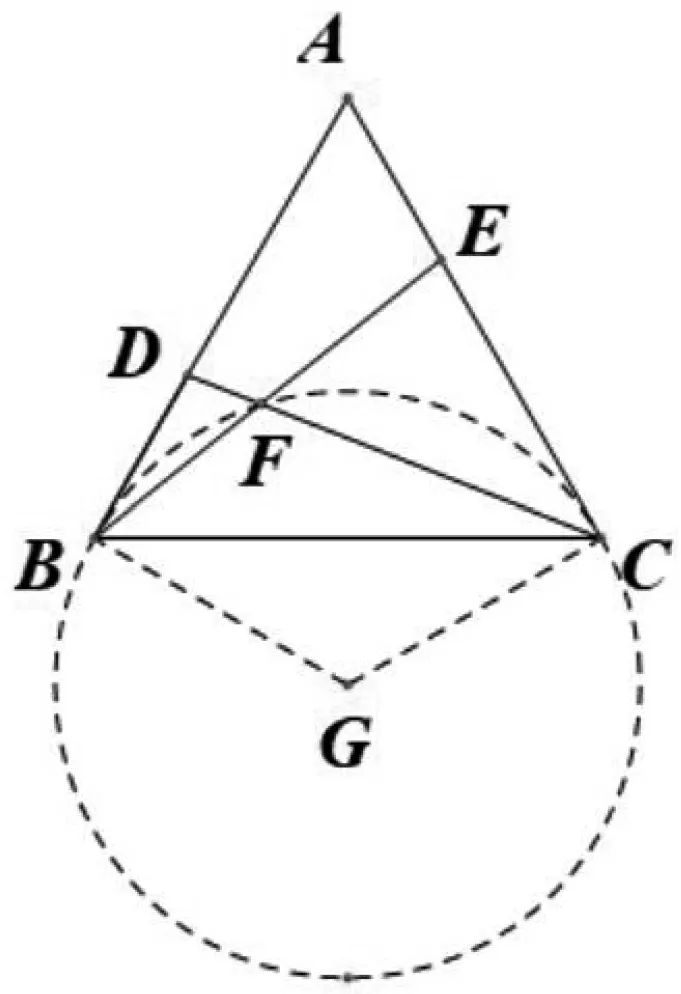
图5
例5 如图5,已知等边ΔABC边长为6,D、E分别为边AB,AC上的动点,且BD=AE,连结CD,BE相交于点F,求点F运动的路径长为________.
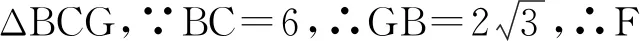
点评:此题中动点F处的∠BFC的度数是定值120°,不再是90°,因此加大了寻找圆心的难度.设隐圆圆心为G,∠BGC=(180°-120°)×2=120°,以BC为等腰ΔBCG的底边,在BC下方构造顶角为120°、底角为30°的等腰ΔBCG,从而找到圆心G,画出隐圆.
设计意图:由“直角对直径”的类型转变为一般的“定角对定边”的类型,让学生体会由特殊到一般的数学思想.
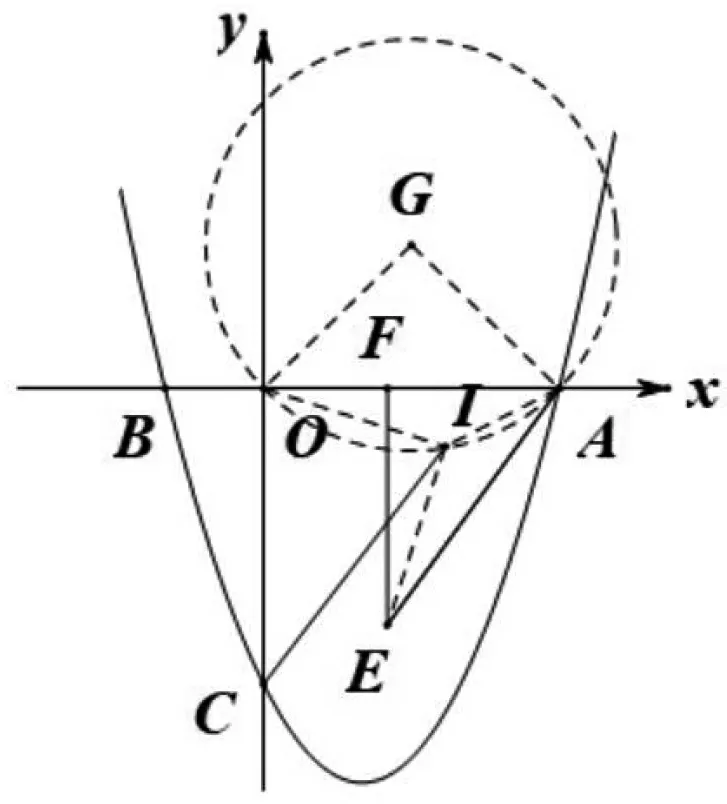
图6
例6 如图6,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,第四象限有一个动点E,满足AE=OA,过E作EF⊥x轴于点F,设F坐标为(t,0),0 点评:此题要求顶点G与动点I的距离最小值,必定要先找到动点I的运动轨迹.由I是内心,可知∠AIE为定角,不难推测是隐圆问题.但是∠AIE的对边AE虽然长度不变,但是位置在变化,以此判断要找的定角并非∠AIE,定弦也不是AE,由AE=OA,AI平分∠OAE,可知ΔAIO≌ΔAIE,∠AIO=∠AIE=135°,而∠AIO的对边AO长度位置均固定不变,此时定角与定弦找到,就可以画出隐圆了. 设计意图:在例5的基础上提升难度,由浅入深,逐渐递进,实现学生解决综合题能力的螺旋式上升. 教师在进行微专题复习设计中,需要有效的落实“以学生为主体”的教学理念,并且在教学中要充分的体现出学生的主体作用,这样才能有效的培养学生的数学核心素养,并充分的发挥出学生的创新精神,并提高学生的自主学习能力.教学实施中应强调:一是因学施教.在进行教学中每一个班级和学生都存在着一定的不同,在复习中的存在问题也不同,进行微专题复习方法的选择应具备一定的针对性,在学生遇到难以解决的问题时,要帮助学生由浅入深的方式来进行问题的解决;二是注重学生思维活动的参与.复习中,应当让学生充分的融入到解题当中,并对题型进行有效的分析和研究,从而真实的投入到复习当中,并真正的了解数学.这样可以有效的促进学生思维的提高,并帮助学生从多方面的角度来进行问题的思考,促进学生数学素养的全面养成.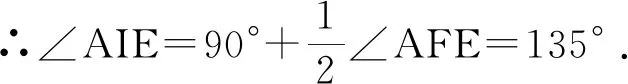
2.微专题复习的教学思考

