立体几何最值问题的四个常见几何视角
广东省广州市广州开发区外国语学校 (510700) 蔡军喜
最值问题作为动态立体几何问题最典型的类型,将空间立体几何中的核心知识和方法融入其中,能有效甄别综合立体几何的数学素养,历来都受到命题者的青睐.对于定量化的动态立体几何问题,构建函数、三角、不等式模型是解决问题常用的途径,利用向量或者几何边角关系构造函数、三角、不等式是解答此类问题的基本策略.但在实际操作中,很多问题需要预先构建几何变换,挖掘几何本质,才能顺利实现代数化处理.本文归纳常见的四种几何变换视角,供参考.
1 展开
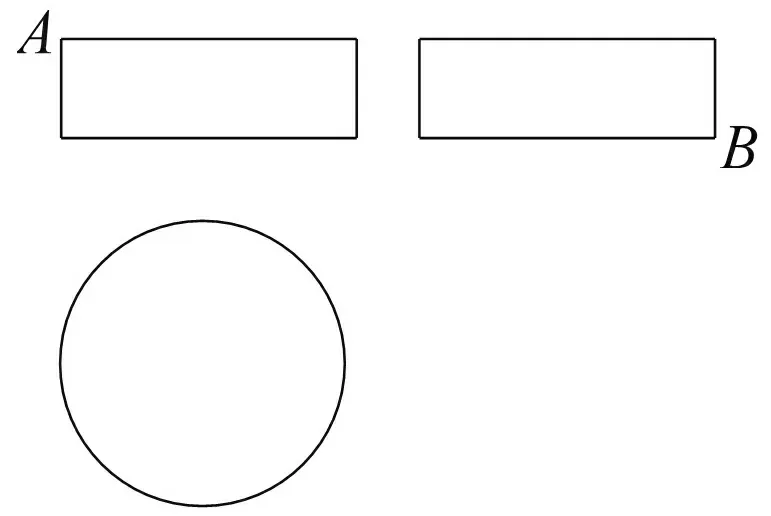
图1
例1 (2018全国卷Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图1.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( ).

图2
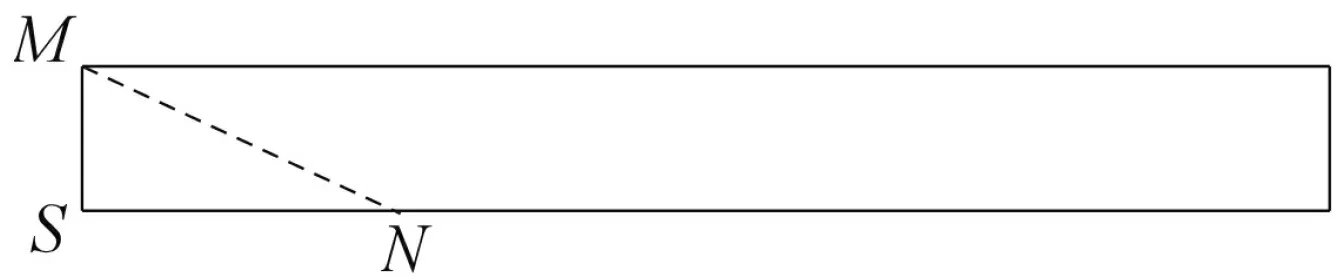
图3
解析:由三视图可知,该几何体为如图2所示的圆柱,该圆柱的高为2,底面周长16.画出该圆柱的侧面展开图,如图3所示,连接MN,则MS=2,SN=4,则从M到N的路径中,最短路径的长度为
点评:两点间直线距离最短,运用这一原理,将立体图形沿某条棱展开成平面图形,化曲为直,化空间为平面是求解此类线段和最值问题的通性通法。需要注意的是同一个几何体沿不同方向展开的情况最值可能会有所不同。

图4
例2 (2006江西卷)如图4,已知正三棱柱的底面边长为1,高为8,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为.

图5
解析:将三棱柱侧面沿棱AA1展开得矩形AA1A2A,因沿侧面绕行两周.故将这个矩形向右平移3个单位与原矩形拼接在一起,如图5所示,因为平面内两点之间距离最短.故所求的最短距路线的长就是大矩形对角线的长.由勾股定理可得对角线长为10.
点评:对棱柱进行侧面展开,化空间为平面,化折为直,再将展开图平移、拼接,使分散的两条折线连在一起.从而使问题得到非常直观的解决.
2 旋转
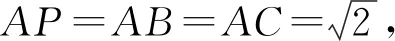

图6

点评:本题本质仍是空间问题平面化,化折为直,不同的是需将两个平面分别绕轴旋转到与第三面共面,从而实现平面内多点共线后的两点间直线距离最短.将多面体的两个面中的一个面沿着它们的公共边翻折或旋转,使这两个面共面,从而使位于这两个平面内的几条线段位于同一平面内,这样就将空间问题转化为平面几何问题,多个面的情形也可类似处理,这既是降维的思想,也是翻折与旋转,变与不变的核心.
3 对称
例4 (2020厦门市一模)已知正三棱柱ABC-A1B1C1的所有棱长均为2,点M,N分别在侧面ABB1A1和ACC1A1内,BC1和B1C交于点P,则ΔMNP周长的最小值为.

图7
解析:如图7,设点P关于侧面ABB1A1和ACC1A1的对称点分别为Q,R,连接QR,则当点M,N,Q,R共线时,ΔMNP周长最小,由于在正三棱柱ABC-A1B1C1中,点P是BC1和B1C的交点,所以点P是侧面BCC1B1的中心,故ΔMNP周长最小时,M,N分别是侧面ABB1A1和ACC1A1的中心,所以ΔMNP周长的最小值为3.
点评:两个动点,三条线段,单纯从代数角度构建函数关系,数式和运算异常复杂,而通过挖掘几何特质,在变化中寻找不变量,点P确定,侧面ABB1A1和ACC1A1固定,对称与平移,动中觅定,变与不变相随.
4 割补
例5 (2010全国卷)已知在半径为2的球面上有A,B,C,D四点,若AB=CD=2,则四面体ABCD的体积的最大值为( ).

图8
解析:


图9
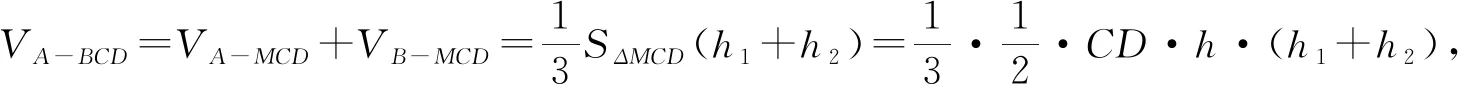
点评:借助常见的几何“母体”,通过还原与补形,使不规则的几何体有体可依,化“无形”为“有型”.同时,平面几何中常见的基本结论: (1)连结两点的线中线段最短; (2) 直线外一点与直线上各点的连线中,垂线段最短.实现联系迁移,有据可依.

图10
例6 (2012上海卷)如图10所示,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a,c为常数,则四面体ABCD的体积的最大值是.

图11

动态立体几何的问题千变万化,有在变化过程中分析空间元素的位置,有在变化中求解某个量的最值或范围,有在变换中分析某个点的轨迹等等.只要我们用心去理解问题,探寻解决问题的方法,反思和总结问题解决的一般性策略,数形相依,动静结合,几何代数互译,那么,我们自然就提高了解决问题的效率,数学思维与视角也会长足进步,更能在问题解决过程中享受数学探究的乐趣.

