基于视觉分区的结构振动模态测试方法

吕钧澔，校金友，文立华，杨永超，刘海晴

(西北工业大学航天学院，陕西，西安 710072)

实验模态分析是获取工程结构动态特性的主要手段，在验证结构动态设计、振动控制及健康监测等领域中发挥着重要作用[1-2]。目前，常见的振动模态测试方法主要有接触式测量和非接触式测量两种。接触式测量方法一般采用加速度传感器和压电陶瓷传感器，需要粘贴在结构表面，会增加结构的附加质量，影响实验测量结果[3]。非接触的测量方法一般采用激光和高速相机等作为测试传感器，均能有效避免附加质量的影响。其中，激光测量一般采用逐点扫描的方式，测试效率较低[4]；采用高速相机可以同时测量多点甚至全场信息，这种高速相机的测量方式也被称为视觉测量方法[5]，已逐渐成为新的研究热点和趋势[6]。

然而，现有的视觉测量方法通常是用相机拍摄被测结构的全局视场，这就导致在测量大型结构或细长结构时，需要用有限的图像分辨率获取更多的视场信息，从而降低了分析区域的有效像素，难以精确测量小位移振动[7]。对此，Wadhwa等[8]提出了一种视频运动放大技术，通过对图像序列之间的局部相位进行滤波和放大，提高了小位移振动响应的信噪比。Poozesh 等[9]将上述方法应用于机翼结构的模态测试，提高了模态振型的辨识精度。该研究工作虽然在一定条件下提升了小位移振动响应的信噪比，但是视频运动放大技术带来的不确定因素较多，例如，需要预先确定放大的频率带宽，且放大系数及中心带宽的选取对位移跟踪精度影响较大[10]。

针对大型结构或细长结构的振动测量，Poozesh等[11]提出了另一种解决思路，即分区测量方法。采用多台相机同时测量结构的不同子区域，通过分区视场之间的重叠区域拼接出全局视场。分区测量增强了子区域图像的空间分辨率，从而有效地提高了测量信噪比。考虑到多台高速相机的成本及协同控制等问题，Patil 等[12]和Srivastava 等[13]提出仅利用一组高速相机进行移动式的测量，并对分区测量数据在频域进行拼接。以上分区测量的研究虽然解决了分区之间的拼接问题，但并未针对高精度测量需求给出具体的分区策略，即如何确定分区视场的大小及分区个数。分区少、视场大时，图像的空间分辨率提升有限；而分区过多、视场小时，相同的振动幅值在图像成像中会倍增。研究表明：相机曝光时间内的高振动幅值会使图像出现运动模糊，导致时域振动位移的失真，从而增大了视觉测量的误差[14]。

为实现高精度的结构振动模态测试，本文提出了一种可估计分区视场大小及分区数的视觉分区方法。通过建立测量视场参数与测量误差的关系，计算出最优的测量视场参数，从而为分区测量方法估计出分区视场大小及分区个数。此方法可以避免分区图像的运动模糊，提高振动响应的信噪比和模态参数的辨识精度。对于视觉测量方法的研究和推广具有重要的理论意义和应用价值。

1 基于分区测量的振动模态测试

分区测量是通过将全局测量视场划分为多个分区，每个分区单独作为测量视场，从而提高分区视场的图像测量精度。首先，对各个分区依次进行振动测试，并估计各个分区的频响函数；然后，对各分区频响函数矩阵进行合并，得到全局结构的频响函数矩阵；最后，通过模态辨识算法获取整体结构的模态参数。

假设将整体结构化分为两个分区视场，如图1所示。其中：分区S1的测量点为 {1,2,3}；分区S2的测量点为 {4,5,6}；第5 点为激励点。

以分区视场S1的振动测量为例，将相机的有效观测区域调整至S1区域采集图像序列。以静止时采集的图像f作为参考图像，振动时采集的图像序列的每一帧作为形变图像g。在图像f中指定一个位置点P(x0,y0) 和以P为中心的图像子区。利用数字图像相关(Digital Image Correlation, DIC)方法，通过最小化匹配准则(式(1))获取g中相对应的位置点P′(x′0,y′0) 和位置点P′子区的形变参数p。匹配准则采用零均值归一化平方和方法[15]建立：

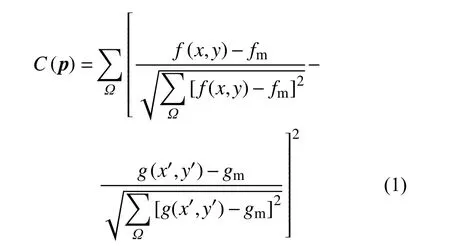
式中： Ω为选择的图像子区；f(x,y)和g(x′,y′)分别为参考图像和形变图像在 Ω区域的图像灰度值；fm和gm分别为f(x,y)和g(x′,y′) 在 Ω区域内的平均灰度值。

采用一阶形变函数描述图像f和g之间的形变关系：

式中：u、v分别为子区中心点在x和y方向的位移分量；ux、uy、vx、vy为图像子区的一阶位移梯度。

因此，形变参数p进一步表示为：

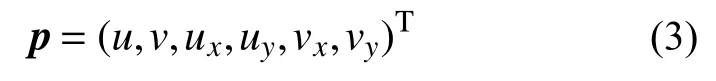
本文采用Newton-Rapshon 迭代方法[15]求解式(1)的最小值问题，可得到沿水平方向的像素位移u，则图像序列的位移为u(t)。

进一步通过图像位移乘以到物理空间的转换系数，即测量视场参数M，来获得每个测试点的振动位移。

然而，上述的分区测量方法，分区视场的大小和分区个数的选取通常是依靠人为经验。若分区视场过小，根据小孔成像原理[18]，相同的振动幅值在分区图像中会放大，易出现图像的运动模糊；若分区视场过大，图像的空间分辨率提升有限，导致测试信噪比低。因此，需要一种可估计分区视场大小及分区个数的视觉分区方法。

2 分区的估计

分区视场大小的估计可转化为对测量视场参数的估计，而分区数可由分区视场大小和已知的全局视场的比值关系得到。本文利用图像的振动测量精度最优，来建立测试视场参数的估计方法。

2.1 图像的振动测量精度与测量视场参数的关系

一般的，对于静态或准静态的图像测量，测量视场参数是影响测量精度的主要因素，且测量视场参数M与测量精度成正相关[19]。然而，对于振动图像测量，除了存在静态测量误差外，还会引起图像采集时的运动模糊。运动模糊程度是与测量精度成负相关的[14]，运动模糊程度也与测量视场参数密切相关。因此，本文从以上两个方面建立测量视场参数M与测量误差 ε的关系。为方便起见，将静态的图像测量的相对误差记为 ε1，运动模糊引起的测量相对误差记为 ε2。

2.1.1 静态图像测量误差与测量视场参数关系

本文采用低分辨率图像生成方法[20]建立静态图像测试误差与测量视场参数的关系。首先，在原始图像中设定感兴趣区域(Region of Interest,ROI)，作为参考图像f；对ROI 平移q像素，形成新的子图像，作为形变图像g。设定不同分解尺度k，分别对图像f和g进行分块矩阵划分，每个小块矩阵为k×k。将每个小块的矩阵图像取平均值，作为一个新的像素。至此，可将f和g变成降采样后的图像fk和gk。此时，fk和gk的测量视场参数为M/k，理论位移为q/k像素，如图2 所示。

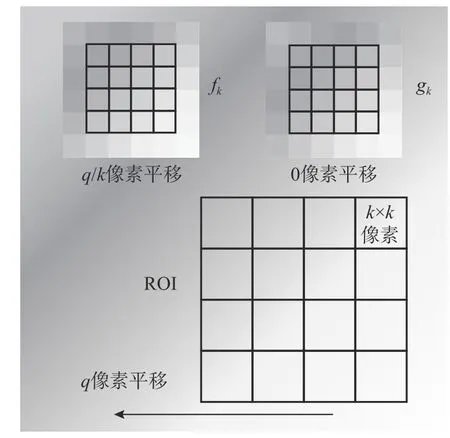
图2 低分率图像的生成过程Fig. 2 Low-resolution image generation

用DIC 方法计算得到fk和gk之间的位移量，记为uk。根据已知的理论位移，即可得到测量视场参数为M/k时的相对误差：

不断改变k的值，并重复此过程，可得到不同测量视场参数下的图像测量误差。通过拟合数据点，以此建立 ε1与M的关系φ(M)：

2.1.2 动态图像测量误差与测量视场参数关系

为描述测量视场参数M与动态图像测量误差ε2的关系，首先引入中间变量w，即图像运动模糊尺度[21]。w与M存在如下关系：

式中：S为物体的振动速度；Te为曝光时间。

通过对参考图像f人为添加模糊尺度w，并沿模糊方向进行退化，形成的退化图像作为形变图像g。此时，图像f到图像g的理论运动偏移量为零，并直接利用DIC 方法计算得到位移uw。所以，动态测试下的相对误差为：

对上述一系列离散数据点进行曲线拟合后，可得到模糊尺度与动态测量精度之间的关系，记为 φ(w)。结合式(10)得到：

在给定测量视场参数M的情况下，当振动速度取最大值(即Smax)时，图像运动模糊尺度最大。考虑到振动过程中，影响图像振动测量精度的为最大模糊尺度。因此，需要确定Smax。一般地，Smax是从结构的最大响应位置点Pm的振动速度历程中获得的。本文采用计算机视觉中的全局光流估计方法确定出Pm的位置，继而得到Smax。则式(12)可变为：

综上所述，图像在振动测量时，需要综合考虑误差 ε1和 ε2，估计出最优的测量视场参数。

2.2 测量视场参数的估计

在不考虑光照、图像噪声和环境因素等情况，可结合式(9)和式(13)，建立图像的振动测量误差 ε关于测量视场参数M的误差函数，即：

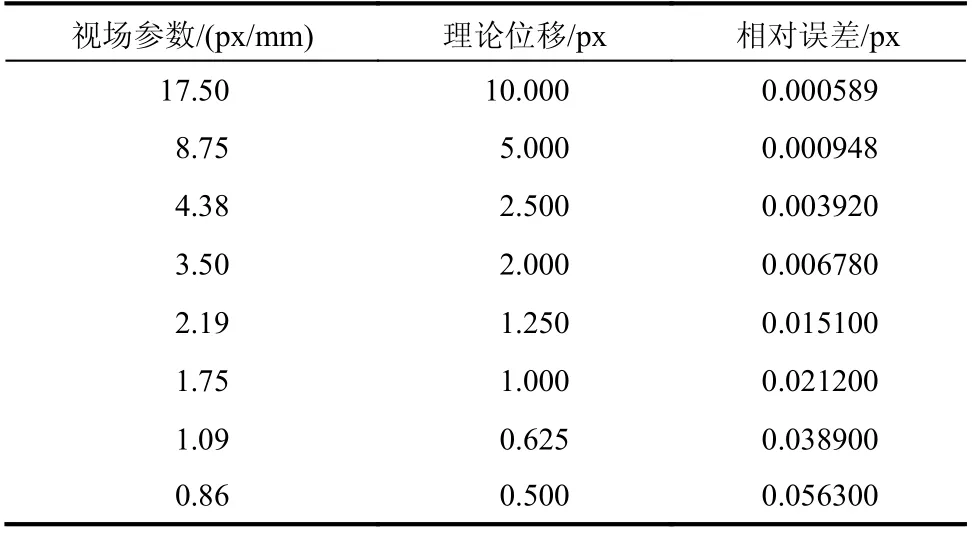
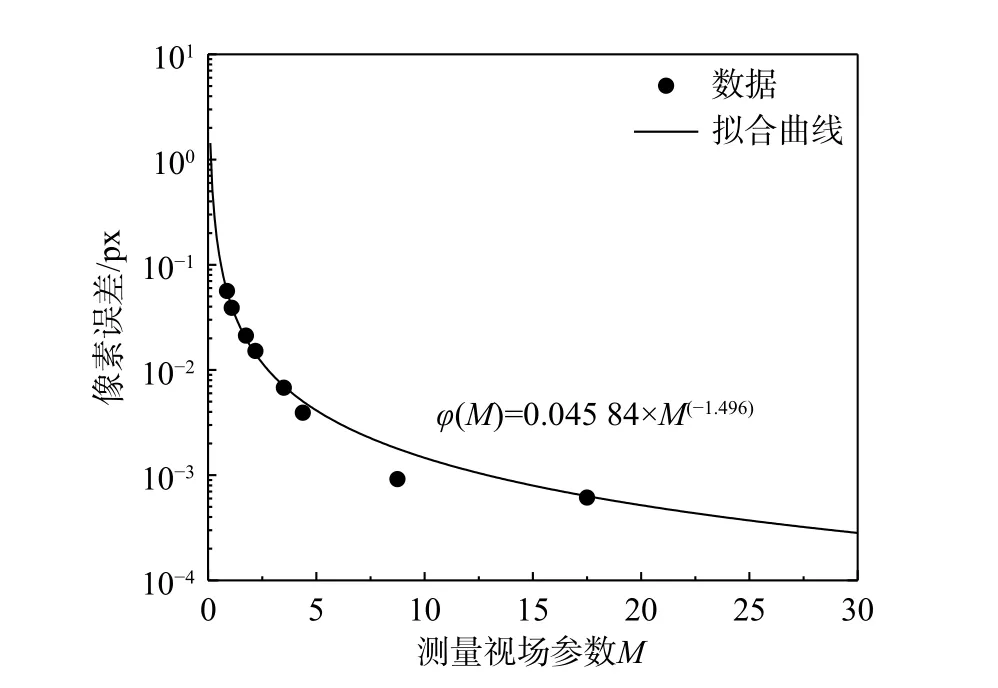
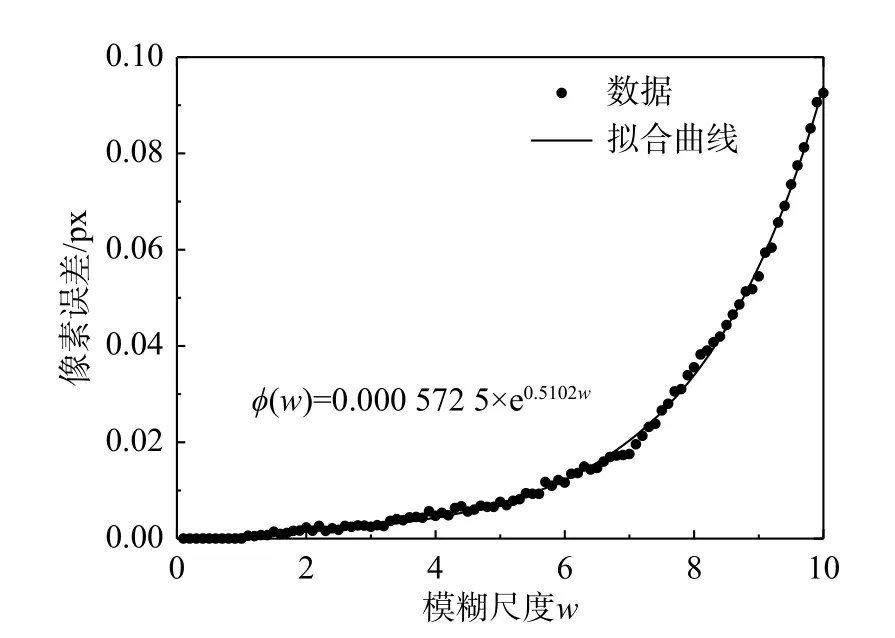
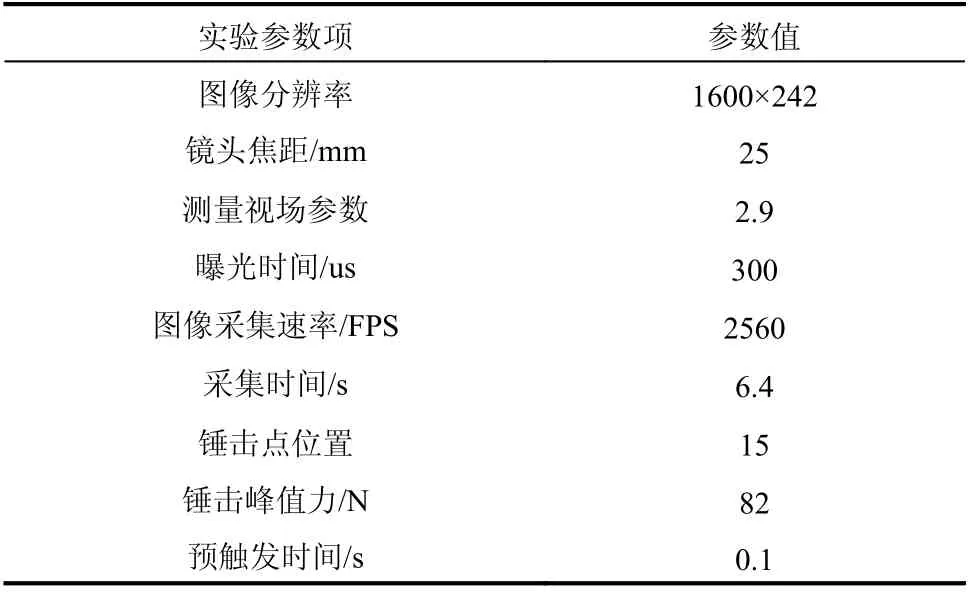
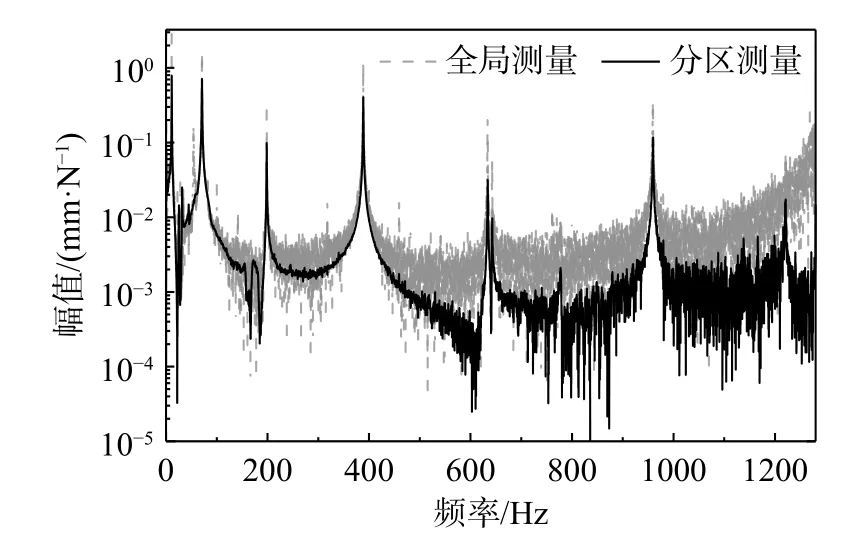
当误差函数 ε取最小值时，得到的M值即为最优的测量视场参数，记为MT。考虑在实际应用中，M的取值区间一般为[0, 30](M>30为微观图像的测量范围)，则求解MT过程即为一元函数ε(M) 在0

在获到测量视场参数MT后，结合图像的分辨率，得到分区视场的实际大小，再根据结构的实际尺寸，即可估计得到分区个数。

综上，针对基于视觉分区的模态测试方法的具体步骤如下：

第一步：对实际的测量对象采集一张静止时刻的图像，根据2.1 节所述方法，分别建立静态测量误差和动态模糊测量误差的关系式，即ε1=φ(M)和 ε2=φ(w)；

第二步：对结构的全局视场进行振动预测试，采用光流法估计结构的运动趋势，得到结构的最大响应位置点Pm及最大响应速度Smax，以此建立图像的振动测量误差 ε关于测量视场参数M的误差函数，即 ε(M)=φ(M)+φ(M)；

第三步：采用最优化方法求解式(14)，得到最优的测量视场参数MT。结合采集图像的分辨率和实际结构尺寸，得到分区测量视场大小及分区个数；

第四步：根据第三步得到的分区估计结果，对测量结构进行分区视场划分，并依次进行振动模态测试，获取分区视场的图像序列和力信号；

第六步：由DIC 图像匹配方法对图像序列进行分析计算，获取分区视场测量点的振动位移。结合力信号估计每个分区内测量点的频响函数；

第七步：合并各个分区的频响函数，得到整体结构的频响函数矩阵，采用Polymax 方法进行模态参数辨识。

3 实验验证

3.1 实验测试系统

为了验证本文所提的视觉分区模态测试方法的可行性，选取典型的细长悬臂梁结构进行实验验证。悬臂梁的长度为450 mm，厚度为3 mm，宽度15 为mm。以悬臂梁结构的厚度侧面作为视觉测量平面，其长细比为150∶1。

实验布置与测试设备连接图如图3 所示，包括IX speed-221 高速相机(满幅1600×1600，帧速率600 FPS)、Dytran 力锤(灵敏度为2.2 mV/N)、Dytran信号调理器、NI 数据采集系统(USB-6218-BNC)和自研制的同步触发器[22](主控芯片TLV3501)。实验中采用固定点激励方式，力锤信号经过信号调理器后：一方面采用NI 数据采集系统被PC 端采集；另一方面经过同步触发器来触发高速相机开始同步工作，将图像序列传输到PC 端，以供后处理分析。

图3 实验系统连接图Fig. 3 Experimental system connection diagram

3.2 测量分区的估计

根据第2 节所述的分区估计方法，首先，建立测量视场参数与测量精度的关系。由2.1 节所述方法，分别得到φ(M) 和 φ(w)。具体为，采集一张被测对象在静止时刻的图像，如图4 所示。为方便估计测量视场参数的初始值，在测量点位置粘贴特殊的圆形标记。已知圆形标记的直径为10 mm，则由式(5)估计得到M=17.5 px/mm。通过2.1.2 节所述方法，得到相应的离散点数据，见表1。

表1 由低分辨率图像生成方法得到的实验离散点数据Table 1 Experimental discrete point data by low-resolution image generation method

图4 测量目标的图像采集Fig. 4 Image acquisition of measurement target

根据实验数据拟合出φ(M)的关系式，结果如图5 所示。其中，φ(M) 的形式为：φ(M)=0.045 84×M(-1.496)。

图5 测量视场参数与测量误差的拟合数据Fig. 5 Fitting data of measurement field parameter and measurement error

进一步，采用2.1.2 节方法得到 φ(w)。给定的模糊尺度为w=0 ～10，间隔步长为0.1，生成相应的模糊图像，根据式(11)计算得到相应的像素误差。图6 分别为离散点数据和拟合曲线 φ(w)，其中， φ(w)=0.000 572 5×e0.5102w。

图6 模糊尺度与测量误差的拟合数据Fig. 6 Fitting data of motion blur and measurement error

下一步，求解Pm区域的最大响应速度Smax。以全局测量视场对悬臂梁进行一次振动测试，全局视场的振动测试的实验参数设置见表2。

表2 Pm 点振动测试的实验参数设置Table 2 Experimental parameter setting of Pm-point vibration test

首先，采用全场光流估计方法，找出Pm的测量位置，如图7 所示，悬臂梁上的矢量箭头表示估计出的运动速度矢量。

图7 光流法的运动趋势估计Fig. 7 Motion trend estimation based on optical flow method

然后，对Pm测量点进行图像的跟踪计算，得到振动历程，经过微分后处理后得到振动速度历程，如图8 所示。对应的最大响应速度为Smax=771 mm/s。

图8 Pm 点的振动速度Fig. 8 Vibration velocity process at point Pm

最后，将Smax和曝光时间Te代入式(14)，得到测量误差关于测量视场参数的误差函数 ε(M)，如图9 所示。

图9 最大响应速度为771 mm/s，曝光时间为300 us 的误差函数曲线Fig. 9 Error function when maximum response speed is 771 mm/s and exposure time is 300 us

在0

3.3 分区模态测试

按照第3.1 节所述的实验设置进行悬臂梁结构的实验模态测试，分别对悬臂梁结构采用全局测量和分区测量，获取到相应的图像序列和力信号。其中，全局测量和分区测量的实验设置参数见表3。

表3 全局测量与分区测量的参数设置Table 3 Parameter setting of global measurement and subarea measurement

对两种测量方法得到的图像序列和力信号分别按照第1 节所述方法进行处理，获取整体结构的频响函数矩阵。以结构上的第9 测量点为例，对比全局测量与分区测量的频响函数，如图10 所示。

图10 悬臂梁第9 测点的频响函数Fig. 10 Frequency response function of 9th measuring point of cantilever beam

可以看出，分区测量的信噪比明显高于全局测量方法。由于过高的噪声值，全局测量的频响函数无法表征出最后一阶的峰值信息，而分区测量方法仍可以清晰表出。

对两种方法得到的频响函数矩阵进行结构的模态参数辨识。以激光位移传感器的测量结果为参照(激光位移传感器采用基恩士LK-G80 型号，标定的测量精度为0.0001 mm)，对比全局测量与分区测量，其模态辨识结果如表4 所示。其中，MAC 值是视觉测量的归一化振型与激光测量的归一化振型之间的模态置信度。MAC 值越接近1，认为振型辨识结果越精确。MACG表示全局测量振型与激光测量振型的计算结果；MACS表示分区测量振型与激光测量振型的计算结果。

表4 悬臂梁的模态参数辨识结果对比Table 4 Modal parameter identification results of cantilever beam

可以看出，对于全局测量方法，第7 阶的模态信息无法辨识，而分区测量方法辨识的模态振型最低MAC 值为0.97。有效提高了结构模态辨识的精度。

4 结论

为了提高视觉方法的结构振动模态的测量精度，提出了一种可估计视场分区的模态测试方法，通过相应的理论分析及实验验证，得到如下结论：

(1)分区测量会提高静态图像的测量精度，但同时也会增大由运动模糊引起的测量误差。采用分区测量方法进行振动模态测试时需要估计出合理的分区视场大小及分区数。

(2)建立误差函数关于测量视场参数的关系时，可避免多次实验测量的数据拟合方式，仅通过采集一张静止时刻的图像建立关系式。

(3)所提的视觉分区测量方法，可以有效提高频响函数的信噪比，辨识出更多的模态信息。在悬臂梁模态实验中，全局测量方法无法辨识的第7 阶模态，使用视觉分区方法仍可辨识，且振型MAC 值为97%，有效提了高结构的模态测试精度。对于视觉测量方法的研究和推广具有重要的理论意义和应用价值。