集中荷载作用下轻骨料混凝土梁受剪承载力计算方法与修正
张望喜,吕炜磊,胡彬彬,王冠杰,易伟建
(1. 湖南大学工程结构损伤诊断湖南省重点实验室,湖南,长沙 410012;2. 湖南大学土木工程学院,湖南,长沙 410012)
钢筋混凝土梁的抗剪承载力问题一直是工程界和学术界的热点。从20 世纪50 年代美国空军的一座仓库的刚架横梁发生典型的斜拉破坏[1]开始,研究者们对钢筋混凝土梁受剪的力学行为开展了大量研究工作,但由于混凝土材料的离散性和受剪问题的复杂性,研究者们基于不同理论给出的各种计算公式不尽相同并且形式复杂难以在工程设计中使用,故各国规范的无腹筋梁受剪承载力计算式大都是采用基于试验数据统计结果确定的半理论半经验公式。
由于钢筋混凝土梁抗剪强度问题的研究主要是在针对普通混凝土梁建立的模型基础上进行,因此,其成果也主要用于普通混凝土梁的抗剪分析和计算。根据极限平衡概念,无腹筋梁受剪时,斜截面上的力有受压区混凝土承担的剪力、骨料咬合力以及纵筋销栓力。与普通混凝土相比,轻骨料混凝土(LAC)的骨料密度小,强度低且弹性模量小,剪切裂缝穿过骨料,破坏面比较光滑,斜截面上骨料咬合作用变小,从而导致斜截面传递剪力的能力降低[2-4]。国内外规范中几乎没有专门针对LAC 梁的抗剪承载力计算公式,通常是在普通混凝土梁抗剪承载力计算公式的基础上,引入折减系数,对混凝土项进行折减,而箍筋项保持不变,由此计算得到LAC 梁的抗剪承载力,其指标的可靠性和精确性很大程度上取决于相应普通混凝土梁抗剪计算模型的合理性和准确性。
由于LAC 梁抗剪承载力计算与普通混凝土梁的区别主要在于混凝土项,因此,需要对LAC 无腹筋梁的抗剪计算模型进行研究。
LAC 根据其组成材料,可以分为全轻混凝土、砂轻混凝土和次轻混凝土。由表1 可以看出,国内外对于LAC 梁的研究主要集中在砂轻混凝土[5-20],而对于全轻、次轻混凝土的研究相对偏少[8,10,13,19-20];对LAC 梁抗剪影响因素的分析主要集中在剪跨比、配箍率、混凝土强度等。

表1 LAC 梁抗剪试验数据Table 1 The data of lightweight aggregate concrete beams
与普通混凝土梁的抗剪计算一样,LAC 梁抗剪承载力受众多因素的影响,试验结果离散性大。基于国内外文献[5 - 20],收集、整理得到238 根集中荷载作用下LAC 梁试验数据。基于变量分离的思想,分析了各主要影响因素对LAC 梁的影响,引入参数剪跨比λ,并考虑到我国使用立方体抗压强度作为混凝土各种力学指标的代表值,通过对试验数据进行拟合,进而在相关经典抗剪模型基础上提出修正计算式。
1 数据的收集与整理
试验数据收集原则:① 试件发生剪切破坏;② 试件为单个或两个集中荷载加载的矩形截面简支梁,且无轴向荷载作用;③ 混凝土采用LAC,受拉纵向钢筋为非预应力变形钢筋;④ 试件信息完整(剪跨比、配筋率、配箍率、截面尺寸等)。
通过考虑影响无腹筋混凝土梁受剪的主要因素,基于试验数据统计分析得到的具有一定安全度的计算式,其适用范围决定于试验参数的取值区间。为了使所建立数据库的数据数量、参数区间、数据有效性具有一定的说服力,根据上述原则,本文基于文献[5 - 20],整理得到集中荷载作用下238 根LAC 梁,见表1。
数据库中,无腹筋梁160 根,有腹筋梁78根;砂轻混凝土梁162 根,全轻混凝土梁66 根,次轻混凝土梁10 根。参数情况如下,混凝土强度等级范围:砂轻LC20~LC90,全轻LC20~LC60,次轻LC55~LC70;配筋率范围:全轻基本均在2.5%以下(其中仅3 根为5%),次轻6.55%(其中2 根为2.89%),砂轻1%~4%(仅有少量率超过4%);剪跨比:全轻2~5,次轻1~4,砂轻2~4。
2 受剪承载力计算式
2.1 相关计算规范和模型
将各国规范建议的抗剪承载力计算公式称为规范计算式,各学者提出的经典抗剪承载力计算式称为计算模型。
2.1.1 JGJ/T 12-2019 计算式[21]
在《轻骨料混凝土技术应用标准》(JGJ/T 12-2019)[21]中,集中荷载作用下当仅配置箍筋时的受剪承载力计算公式是在《混凝土结构设计规范》(GB 50010-2010)基础上,将混凝土项进行折减,箍筋项保持不变得到:

式中:λ 为计算截面剪跨比,可取λ=a/h0,λ≤1.5 时令λ=1.5,λ≥3.0 时令λ=3.0;a为集中荷载作用点至支座截面或节点边缘的距离;ft为LAC 轴心抗拉强度设计值;b为计算截面宽度;h0为计算截面有效高度;Asv为配置在同一截面内箍筋各肢的全部截面面积;s为沿构件长度方向的箍筋间距;fyv为箍筋的抗拉强度设计值。
2.1.2 ACI318-19 计算式[22]
ACI318-19[22]抗剪承载力公式将混凝土梁的抗剪承载力分为混凝土项和箍筋项,其中混凝土项计算方法根据配箍率的大小,分为2 大类,当配箍率大于最小配箍率时,有简化方法和一般方法2 种;公式中箍筋项的计算公式是基于45°桁架理论模型得出,即(仅配置箍筋时):
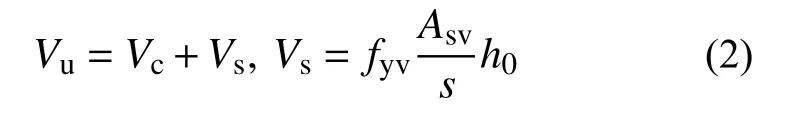
当Av≥Av,min时:
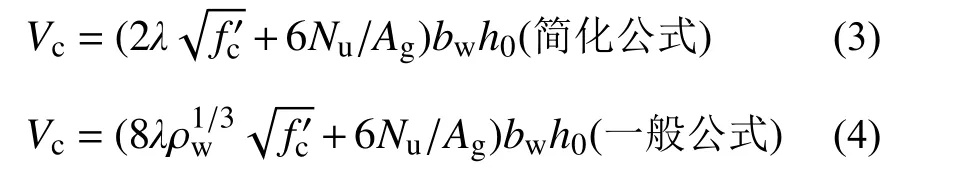
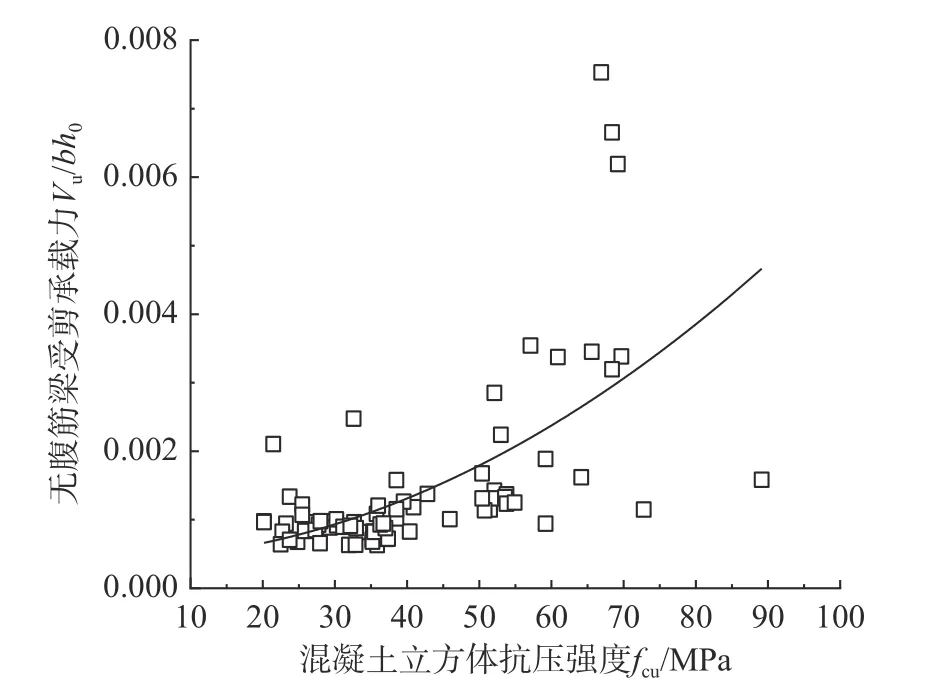
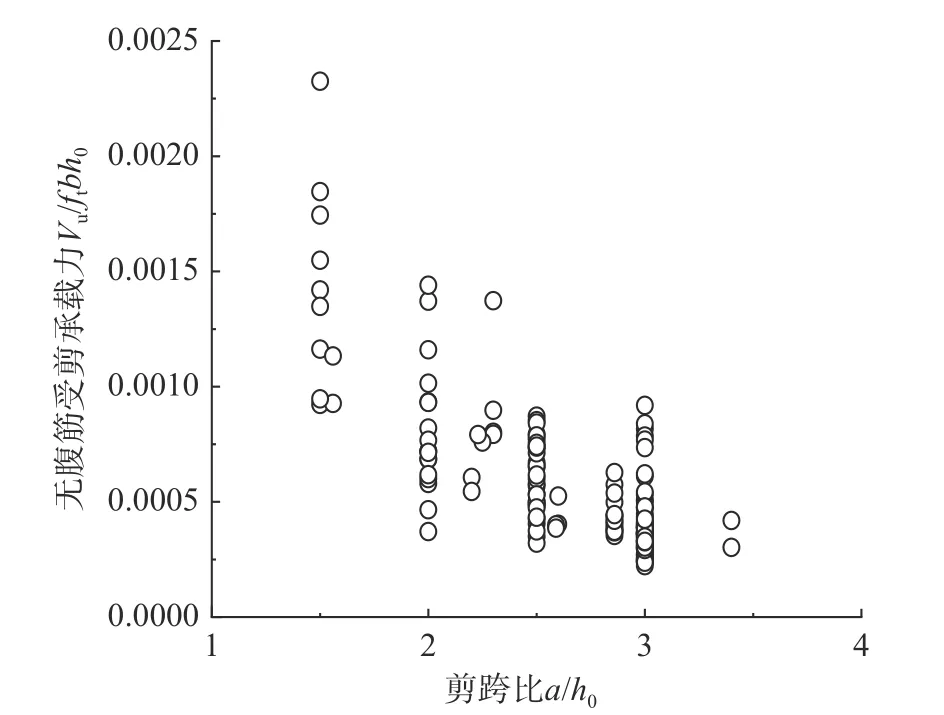
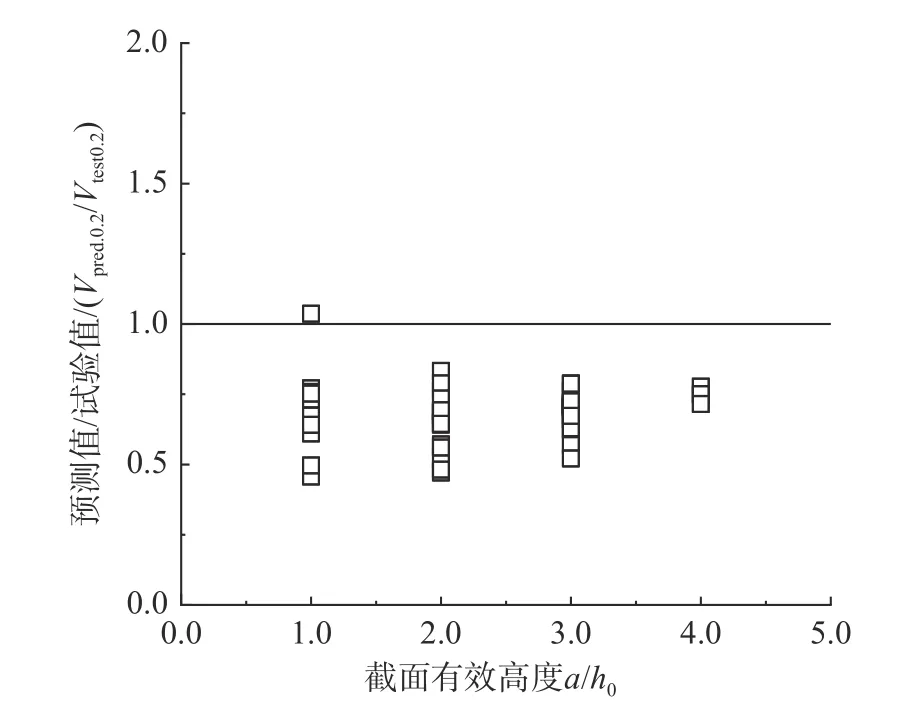
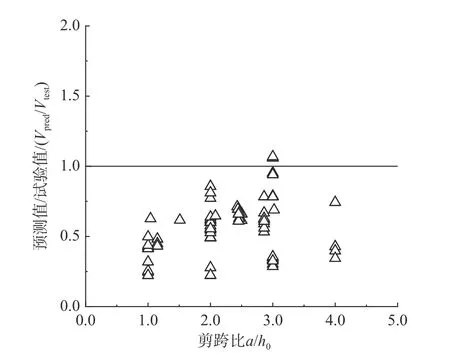
当Av 2.1.3 BS8110-1:1997 计算式[23] BS8110-1:1997[23]斜截面抗剪计算公式中的混凝土项和箍筋项还需要分别除以材料分项系数1.25、1.15,表达式为: 式中:ρw为纵筋率,最大纵筋配筋率要求为3%;fcu为立方体抗压强度标准值;当LAC 强度等级不低于25 MPa 时,混凝土项乘以0.8 的减系数;其他符号的含义与式(2)相同。 2.1.4 Bazant-Sun 计算模型[24] Bazant 和Sun 应用非线性断裂力学确定了考虑尺寸效应的计算表达式[24]: 式中:ρ 为纵筋配筋率;fc′为混凝土圆柱体抗压强度平均值;da为骨料最大粒径;其他符号同式(1)。 2.1.5 Kim-Park 计算模型[25] Kim 和Park 先经过简单分析确定公式基本形式,然后进行统计回归分析确定常数,提出与最大骨料粒径无关的新的考虑尺寸效应的表达式[25]: 式中:ɑ为破坏模式指标,当1≤λ≤3 时,ɑ=2-λ/3,当3≤λ 时,ɑ=1;其他符号的含义与式(7)相同。 2.1.6 Rebeiz 计算模型[26] Rebeiz 经回归分析得到抗剪承载力计算式[26]: 式中:Ad为形状调整系数,当1≤λ≤2.5 时,Ad=λ,当λ≥2.5 时,Ad=2.5;其他符号的含义与式(7)相同。 2.1.7 Vecchio-Collin 计算模型[27] Vecchio 和Collin 基于修正的压力场理论提出了考虑尺寸效应的受剪承载力计算式[27]: 式中:sx为裂缝间距,可取为0.9h0;agg为骨料粒径,当斜裂面穿过骨料,骨料粒径不成为控制因素时,可取为0;其他符号的含义与式(7)相同。 不同规范与计算模型对受剪破坏机理的理解和考虑的影响因素的异同在受剪承载力计算公式中均有所体现。所引用的相关规范计算式和计算模型所考虑的影响因素的整理如表2 所示。 表2 各规范、模型计算公式及考虑的因素Table 2 The formulas and factors considered in various specifications and models 通过计算值与试验值的比值来对规范和计算模型进行误差分析。由于计算模型是基于试验数据进行回归得到的平均值表达公式,故根据设计值、标准值、平均值与变异系数的关系,将各规范公式转化为由平均值表达的公式[28]。LAC 相关强度换算公式[16]:=0.95fcu、ft=0.26。式(1)、式(5)和式(6)对应的平均值表达的公式依次为式(12)、式(13)和式(14): LAC 梁的剪切破坏机理与普通混凝土梁本质上一样,影响因素较多,各影响因素相互交织导致其机理难以确定,为了评估上述规范计算式和计算模型的误差,基于变量分离的思想,对计算值与试验值的比值随各设计参数的变化趋势进行分析。 基于数据库中160 根无腹筋梁的试验结果,计算得到的预测值与试验值之比Vpred/Vtest随试验参数变化的趋势如图1 所示。从图1 可以看出,Vecchio-Collins 计算模型[27]的保守数据估计点最多,而其余计算模型整体上偏不安全,这是因为,相较于普通混凝土梁,LAC 梁的骨料强度低,且由于轻骨料与其他组分的密度相差较大,LAC拌和物存在比普通混凝土更严重的分层问题,因此,一般而言,LAC 梁的抗剪承载力低于同强度的普通混凝土梁。在各规范计算式中,ACI 318-19[22]对于LAC 梁的预测结果最不理想,非保守数据估计点所占比例最大。从图1 也可以看出,各因素对LAC 梁抗剪承载力变化趋势的影响也不尽相同。随着剪跨比的增大,各规范计算式和计算模型的非保守数据估计点数量显著增加,安全性降低,特别是当剪跨比大于3 时,Vpred/Vtest明显增大。对于JGJ/T 12-2019[21],由于在无腹筋梁抗剪承载力公式中没有计入纵向受拉钢筋配筋率的影响,故,随着ρ 值的增加,保守数据估计点数量逐渐增多。虽然基于普通混凝土梁抗剪试验回归得到的Bazant-Sun[24]、Kim-Park[25]、Vecchio-Collins[27]计算模型均考虑了剪切尺寸效应的影响,但当梁截面有效高度增加时,除了Vecchio-Collins 计算模型[27],其余计算模型都未能偏安全地预测LAC梁的抗剪承载能力。即使LAC 梁的抗剪机制与普通混凝土梁在本质上一样,但由于轻骨料的材性与普通混凝土不同,且需要特殊的施工工艺(轻骨料需预先吸水),故而两者的抗剪承载力有所差异。 图1 预测值与试验值之比Vpred/Vtest 随试验参数的变化趋势Fig. 1 The trend of Vpred/Vtest with test parameters 结合表3、表4 的分析结果可知,所选各国规范计算式和计算模型均偏于不安全。对于砂轻混凝土、全轻混凝土,ACI 318-19[22]Vpred/Vtest平均值分别为2.2、2.0,变异系数为0.49、0.41,非保守估计数据点所占比例为83%、87%,因此预测结果最不理想;JGJT 12-2009[21]和BS 8110-1:1997[23]Vpred/Vtest平均值分别为0.88、0.95 和0.92、1.07,非保守数据估计点所占比例分别高达39%、42%和52%、56%,预测结果同样不理想;针对普通混凝土梁建立的抗剪承载力计算模型Bazant-Sun 模型[24]、Kim-Park 模型[25]、Rebeiz 模型[26]、Vecchio-Collins 模型[27]的计算结果整体偏大,Vpred/Vtest平均值分别为1.15、1.10 和1.23、1.18 以及1.28、1.23 和0.82、0.87,非保守数据估计点所占比例分别为72%、64%和78%、77%以及78%、79%和38%、35%,这也从侧面说明了骨料对抗剪承载力的影响。由于无腹筋LAC 梁数据中次轻混凝土梁仅有2 根,故此处未单独列出其计算结果。 表3 砂轻混凝土试件计算结果Table 3 The results of sand-lightweight concrete specimens 表4 全轻混凝土试件计算结果Table 4 The results of all-lightweight concrete specimens 虽然LAC 梁抗剪承载力受到众多因素的影响,但各因素对梁抗剪承载力的影响程度并不相同。从图1 和图3 可知,剪跨比λ 对无腹筋梁抗剪承载力有显著的影响,当λ<3 时,随着λ 的增加,梁的抗剪承载力降低明显,当λ≥3 时,梁的抗剪承载力基本不受剪跨比的影响。 图2 无腹筋梁受剪承载力与混凝土强度的关系Fig. 2 Relationship between shear capacity and concrete strength of beams without web reinforcement 图3 无腹筋梁受剪承载力与剪跨比的关系Fig. 3 Relationship between shear capacity and shear span ratio of beams without web reinforcement 从前述对数据库中砂轻LAC 试件和全轻LAC 试件的分析结果来看,在所讨论的计算模型和规范计算式中,Vecchio-Collin 计算模型[27]的预测结果最好。对于砂轻LAC 试件,其预测值与试验值比值的平均值为0.82,非保守点所占比例最小,为38%;对于全轻LAC 试件,其预测值与试验值比值的平均值为0.87,非保守点所占比例同样最小,为35%;并且相较于所讨论的其他计算模型和规范计算式,Vecchio-Collin 计算模型[27]形式简单,便于工程运用。因此,本文基于Vecchio-Collins 计算模型[27]进行修正。 由于LAC 骨料密度小,强度低且弹性模量小,剪切裂缝穿过骨料,故计算其受剪承载力时,取agg=0,连同sx=0.9h0代入式(11),即得: 将式(15)代入式(10),得: 从图1、图4(a)可知,本文所建立的数据库中集中荷载作用下LAC 无腹筋梁受剪承载力与截面尺寸并无明显的关系[5,7-17,19-20]。从梁的抗剪机理来看,对于普通混凝土无腹筋梁,大构件会出现宽的裂缝,裂缝宽度越宽,骨料咬合力会越小,从而导致梁的受剪承载力减小,所以,在普通混凝土无腹筋梁中存在着明显的尺寸效应。而对于LAC 无腹筋梁而言,其骨料密度小,强度低且弹性模量小,剪切裂缝穿过骨料,骨料咬合力的作用很小,所以,在LAC 无腹筋梁中尺寸效应并不显著。从图4(b)可以看出,LAC 有腹筋梁的剪切破坏尺寸效应同样不明显[5-6,11-12,16-17,18-19],故常规LAC 梁的抗剪设计可不考虑尺寸效应。 图4 梁受剪承载力与截面有效高度的关系Fig. 4 Relationship between shear capacity and section effective height of beams 考虑到剪跨比a/h0对LAC 无腹筋梁受剪承载力有较大的影响,引入参数λ=a/h0对式(16)进行变形,如式(17)所示: 因此,文中假定在集中荷载作用下,LAC 无腹筋梁的抗剪承载力计算式为: 式中:A、B为待定常数;λ 为剪跨比;fcu为立方体抗压强度值;b为截面宽度;h0为截面有效高度。 利用建立的数据库,对式(18)进行非线性拟合,得:A=5.1,B=-4.2。为了使非保守数据估计点所占比例不高于5%,按偏下限的取值方法,经试算,当A=9.2 时,非保守数据点所占比例为4.38%,故,得到的以平均值表达的修正计算式为: 鉴于各国抗剪公式的普遍形式为Vu=Vc+Vs,以修正计算式为混凝土项的平均值表达公式(20),以此来计算有腹筋梁的承载力。 从梁的受剪过程可以知道,随着荷载的增加,梁中斜裂缝的宽度会扩展,数量和形状会发生变化。荷载继续增加,斜裂缝宽度会继续扩展。已有的研究成果表明[29-31],在构件正常服役周期内,裂缝宽度与荷载水平存在对应关系,即在正常使用阶段内,不同受荷阶段,对应着不同的荷载宽度。我国《混凝土结构设计规范》(GB 50010-2010)规定[32]对于各种受力构件,在短期荷载作用下的最大裂缝宽度限值应为0.2 mm。因此,我国习惯将斜裂缝宽度为0.2 mm 时对应的荷载定义为临界斜裂缝荷载。若在某个阶段的荷载值小于临界状态下的荷载值时,则可以判断相应荷载下的裂缝宽度小于临界荷载下的裂缝宽度,即该荷载值下的裂缝宽度小于0.2 mm。基于本文收集的试验临界裂缝荷载数据,根据文献[16, 33]所述方法验算式(20)在使用荷载作用下的斜裂缝宽度能否满足要求。式(20)的预测值Vpred0.2与试验结果Vtest0.2的比值如图5 所示。可见,式(20)能保证几乎所有试验梁在使用荷载作用下斜裂缝宽度小于0.2 mm。 图5 LAC 梁正常使用状态验算Fig. 5 Checking calculation of LAC beam under normal service condition 对式(20)进行有腹筋梁极限承载力验算,预测值Vpred与试验值Vtest的比值如图6 所示。可知,以修正计算式为混凝土项,箍筋项采用45°桁架模型的计算公式可以较好地预测LAC 梁的抗剪承载能力。 图6 有腹筋梁承载力验算Fig. 6 Checking calculation of bearing capacity of beam with web reinforcement 综上所述,以修正计算式为混凝土项的平均值表达公式具有较高的安全性。根据设计值、标准值、平均值与变异系数的关系,考虑到我国设计中使用的是混凝土轴心抗压强度值,参考相关文献[16],通过有关学者基于大量试验数据建立的混凝土强度换算关系,fc=0.93fcu,将以修正计算式为混凝土项的平均值表达公式(20)中的fcu,m换算成fc,m,并将该式转化为以设计值表达的式(21)以便于工程设计使用: 式中,剪跨比λ 应满足,1≤λ≤3,当λ≥3 时,取λ=3,当λ≤1 时,取λ=1;LAC 强度等级不应低于LC20,且不应高于LC90。 通过基于建立的LAC 梁试验数据库,对各国规范建议式和经典的钢筋混凝土梁抗剪承载力模型误差进行评析,得到的结论如下: (1) 各国规范计算式中,无论是对砂轻LAC还是全轻LAC,JGJ/T 12-2019、ACI 318-19、BS 8110-1:1997 预测结果中非保守数据估计点所占比例均较大,其中ACI318-19 非保守数据估计点数量最多,分别高达83%和87%。 (2) 计算模型Bazant-Sun、Kim-Park、Rebeiz、Vecchio-Collins 中以Vecchio-Collins 计算模型非保守数据估计点所占比例最小,对于砂轻LAC 为38%,对于全轻LAC 为35%,但整体来说,针对普通混凝土梁建立的抗剪承载力计算模型的预测值均偏不安全。 (3) 根据就各主要影响因素对试件受剪承载力影响的分析结果,参照Vecchio-Collins 计算模型的形式,引入参数剪跨比λ,并考虑到我国使用立方体抗压强度作为混凝土各种力学指标的代表值,基于对收集、整理得到的集中荷载作用下LAC 无腹筋梁试验数据的非线性拟合,提出修正计算式,且预测值具有较高的安全性(非保守数据估计点所占比例为4.38%)。 (4) 鉴于各国抗剪公式的普遍形式,提出了以修正计算式为混凝土项,箍筋项采用45°桁架模型建立的计算公式,并利用搜集的集中荷载作用下临界裂缝荷载试验数据和有腹筋梁承载力试验数据,从正常使用状态裂缝宽度控制和有腹筋梁承载力两方面对修正式进行验算,结果表明,所建议的修正计算式可以较好的满足要求。结合我国设计习惯,将修正式换算为以设计值表达的LAC矩形截面有腹筋梁在集中荷载作用下的抗剪承载力公式,便于工程应用。


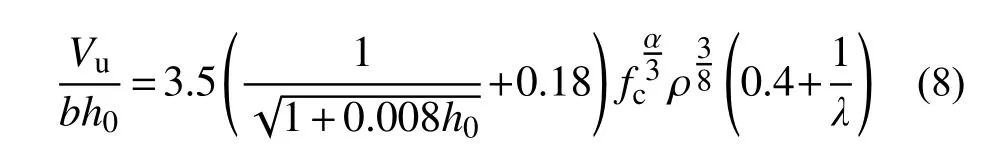
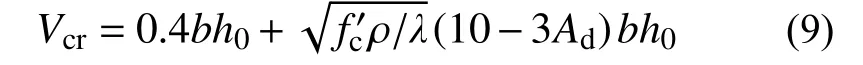

2.2 各规范计算式与计算模型比较

3 计算式和计算模型误差分析与修正
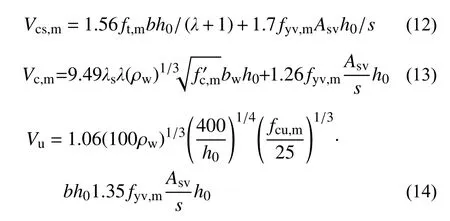
3.1 误差评估



3.2 计算模型修正


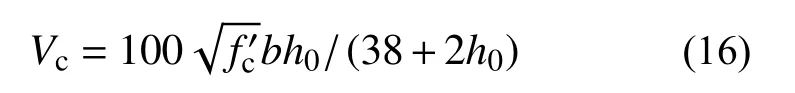



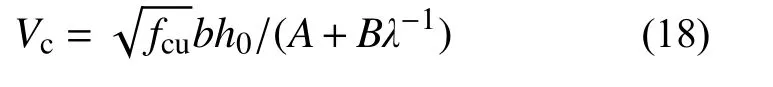

4 修正式验算与讨论
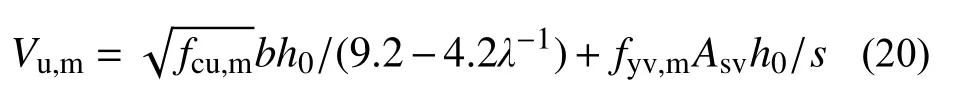

5 结论

