深化“新常规” 彰显“深思维”

杨晴宇

［摘 要］低学段的学生在生活中对空间与几何知识仅有初步的感受。通过复习立体图形的知识，帮助学生利用“新常规”沟通平面图形与立体图形之间的关系，使他们进一步完善对几何图形的建构，进而从多角度“再认识”立体图形，最终在合作交流中深化思维。

［关键词］立体图形；复习教学；数学思维

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2022）35-0037-04

“图形与几何”复习课牵扯到的知识点既多又杂。为了摸清学生的思维起点，笔者做了一个前测，了解到有85%以上的学生能掌握复习课的知识点。若在课堂上一一再现这些知识点的话，势必会占用大量的时间，但若仅仅将知识点简单再现，就会使教学浮于表面。那么，如何处理好“有限时间”与“大量知识点”、“知识点”与“知识网”、“基础”与“提升”、“低阶思维”与“高阶思维”的关系，这是需要教师好好思考的。

于是，笔者在设计“立体图形的认识（总复习）”时，充分考虑用好“新常规”，从预习导航、课堂支持、反思提升三方面考虑，做了调整，以提升学生辨析、推理、描述等能力。

一、把握核心，强化“再认识”

精心选择内容，加强对核心知识的深度理解，可以避免表面教学、表层教学、表演教学。教师应精心设计复习课，对于一般的内容点到即可，而对于核心内容则要详细展现，多角度深化学生对它的认识。为此，笔者设计本节课时，抽取学生画的不同层次的、具有代表性的思维导图，及时调整教学设计并有针对性地对教学进行预案。

【教学设计片段1】

（课前，笔者让学生利用思维导图，回顾并整理已学过的立体图形的特征。）

师：我们学习了长方体、正方体、圆柱、圆锥这些立体图形，现在我们就围绕这些立体图形来上一节总复习课。

（如图1所示，笔者呈现学生的思维导图作品，类型有知识树、列表、画图。学生上台汇报，接着进行集体评价。）

【设计意图】让学生在课前独立整理立体图形的特征，把对基本知识点的回忆提前，课堂上直接省略这一步，以节约时间。而学生通过制作思维导图，有效整合了分散的知识点。

【教学后记】由于课前时间充裕，学生独立梳理的知识点较为完善。学生由点状思维、中心思维逐步向发展性思维转变。大部分学生采用了表格的形式从点、线、面的数量和特征来整理，有的学生用结构图来整理，还有的学生用知识树、鱼骨图等进行梳理。课堂上学生自信地结合自制的思维导图，向大家做了介绍，其余学生在听他人汇报的同时再次回顾了知识点，对自己有遗漏或欠缺的地方，利用课后时间做了修正。此环节，可以较好地解决“有限时间”与“大量知识点”的矛盾，培养了学生的总结性思维。

二、建立联系，建构“知识网”

教材上所呈现的复习内容是对各图形知识点的一一罗列，如果仔细分析，不外乎是从三视图、展开图、图形运动三个角度开展的，如果把这节课的立足点定位在沟通平面图形与立体图形之间的关系，那么这节复习课就能真正实现学生对几何图形的“再认识”，帮助学生建构更完善的几何图形知识结构。学生真正意义上的“深思维”，需要建立在教师的深度教、引导的基础之上，发展学生“深思维”不是一味地让学生自主探讨，而是让他们在教师引导下对知识进行“层进式”“沉浸式”和“高阶思维式”的持续探讨。

【教学设计片段2】

师（出示有同一个顶点的三条线段，其中两两相互垂直，线段略）：这个立体图形有部分线段被遮住了，猜猜它是什么？

生1：若三条线段是相等的，以三条线段为棱画图，就是一个正方体；若其中一条线段与另外两条长度不同，以三条线段为棱画图，就是一个长方体。

师：从这个过程中，你能看出正方体和长方体之间有什么联系吗？为什么说正方体是特殊的长方体？

生2：正方体具有长方体所有的特征，可以用集合图来表示正方体是特殊的长方体。

【设计意图】长方体的长、宽、高极其重要，一旦它们确定了，就能确定其6个面的形状，同时也能确定其形状；反之，长方体的形状发生变化，那么它的长、宽、高也一定发生变化，它们三者是相辅相成的。利用这一特点，再通过动画演示，能让学生直观感受长方体与正方体之间的联系，初步感受线、面、体间的关系，为深化学生的思维添加基石。

【教学后记】在实际教学过程中，根据三条线段的位置、长度关系来猜图形，学生一猜即中，因为他们有了初步的空间观念。俗话说眼见为实，笔者利用动画演示长方体到正方体的变化，可使学生将正方体记忆为长、宽、高都相等的长方体，避免了生搬硬套的理解和记忆。

【教学设计片段3】

练习1：有一个长方体，图2的左边分别是从它前面和上面看到的图形，那么右边哪个图形是从它右面看到的？

师：说说你是怎样想的？

生：根据从前面、上面看到的图形，可以确定长方体的长、宽、高，进而确定长方体的形状。

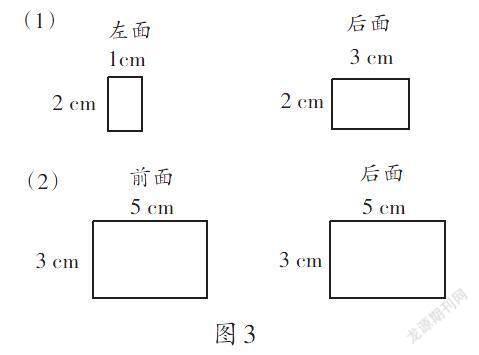
练习2：根据已知的两个面（如图3），你能确定长方体的形状吗？

师：练习2中，这两个分别是怎样的长方体？它的长是几，宽是几，高是几？

师：要知道怎样的两个面才能确定长方体的形状？为什么？

生（小結）：只有知道相邻的两个面，才能确定长方体的长、宽、高，进而确定它的形状。

【设计意图】练习2中，笔者设计的两道题分别是已知相邻两个面和已知相对两个面，能否确定长方体的形状，让学生在脑海中“刻画”图形，最终明白只有确定了长方体的长、宽、高，才能知道其形状，得出的结论才是精准的，从而更好地发展学生的空间观念。如此，让学生再次感受到线、面、体间的关系，使思维从具象向抽象过渡，构建全面的知识网。

【教学后记】在教学过程中，要让学生真正参与学习的过程。如已知两个相邻的面，学生能推出长方体的长、宽、高，进而确定长方体的形状。已知两个相对的面，是无法确定长方体的形状的，这也是学生的学习难点。在这过程中，笔者及时利用动画演示，帮助有困难的学生，让学生的思维逐步得到提升，真正做到让学习可见、让思维发展。

【教学设计片段4】

（任务1）

师：除了从三视图的角度可以沟通平面图形和立体图形之间的联系，还可以从什么角度来沟通它们之间的联系呢？

师（出示图4）：判断下列图形哪些是正方体的展开图。

生1：前面两个是，最后一个不是。

师：最后一个为什么不是？

生2：最后一个找不到3组相对的面。

生3：有3组相对的面才能折叠成正方体。

（任务2）

师（出示图5）：下列图形是长方体的展开图吗？如果是，在头脑中想象折叠的过程；如果不是，怎么改才能折成长方体？

生4：由平面图形折叠成立体图形，不仅要找出3组相对的面，还要考虑面与面之间的大小关系。

（任务3）

师（出示图6）：下面左边4个正方体中，有一个是用右边的图形折叠而成的。先猜一猜是哪一个，再折一折。

（四个选项都有学生选，让选择①、③、④错误选项的学生分别说说自己的想法。）

师：他们说的对吗？如果在脑中想象折叠过程有困难，还可以怎么做？

生5：动手折一折来验证。

师（引导学生小结）：把立体图形展开就得到平面图形，反之，将一个平面图形折叠，也可以得到立体图形（如图7）。

【设计意图】探究平面图形和立体图形之间的联系，教材上的安排是先复习长方体的展开图，再复习正方体的展开图。然而事实上，正方体的展开图比长方体的展开图简单些，笔者对教学内容进行调整并设计3个任务，让学生围绕展开图进行研究，让学习更具思考价值和思维广度。

任务1通过正方体展开图，让学生感受到只要确定3组相对的面，就能折叠出正方体。任务2通过长方体展开图，让学生进一步意识到，在折叠时不仅要考虑相对的面，还要考虑面与面之间的大小关系，这样，又回到探究长方体的棱的相关问题，使学生在思考的过程中能够巩固对长方体和正方体特征的認识。任务3主要让学生根据正方体的展开图，通过想象与推理找到与展开图相对应的正方体，具有一定的挑战性和趣味性。

在教学时，教师除了要为每个学生提供足够的研究时间和空间，还应鼓励学生在想象的基础上动手操作，这照顾到空间想象能力较弱的学生，有助于他们加深对展开图与立体图形对应关系的认识，发展空间观念和推理能力。

【教学后记】任务1的3个图形，由易到难，要求学生既要能根据展开图想象将其还原成正方体，又要判断出6个面的相对关系。任务2不仅要求学生要确定3组相对的面，还要考虑面与面之间的大小关系，再通过调整面的大小，使之可以折叠成长方体。任务3为教材上的思考题，学生可通过推理或排除的方法找到正确选项，可训练学生观察、分析、推理、表达等能力。这样的教学设计，使学生通过逐级训练，逐层推进地学习，提升空间想象能力，拓展思维深度。

三、丰富变化，促进“再生长”

精编综合性练习题，具有以简约的素材承载众多的知识点的特点，可有效激发学生的批判性思维和创造性思维。教师在教学中构建有深层认知意义的情境，为学生灵活解决实际问题、发展空间想象能力、培养合理的联想能力起到重要作用。

【教学设计片段5】

师（出示图8）：下面两条线段可以形成什么平面图形？这个平面图形再通过运动能得到什么立体图形？圈出这个立体图形可能是什么物品。

生1：可以形成三角形，三角形通过旋转可以得到圆锥。

师：是怎样的圆锥呢？

生1：底面半径为12 cm，高为24 cm的圆锥，可能是生日帽。

师（做出旋转手势）：通过不同方式的旋转还能得到怎样的圆锥？

生2：能得到底面半径为24 cm，高为12 cm的圆锥，可能是斗笠。

师：还能形成什么平面图形？

生3：长方形，通过旋转得到底面半径为12 cm，高为24 cm的圆柱，可能是积木桶，也可能是花瓶。

生4：通过旋转还可以得到底面半径为24 cm，高为12 cm的圆柱，可能是蒲团。

师（小结）：在研究形的问题时，不能忘记数，只有数形结合，描述立体图形才会更精准。

【设计意图】此题的设计，又一次引发学生思考，让学生感受从线可以想到面、体，形成从一维到二维，再到三维的认知体验。

学生通过把三角形和长方形以不同的边为轴旋转一周，得到不同的圆锥和圆柱，进一步加深对圆锥和圆柱特征的认识。这样的设计同时启发学生关注数据信息，注意数形结合，只有将图形的认识和实际结合起来，描述才会更精准。

【教学后记】此题的训练很好地构建了圆柱、圆锥的“知识点”与“知识网”之间的联系，同时也协调了“低阶思维”与“高阶思维”的关系。线→面→体的想象与生活实物紧密联系，进一步沟通了空间几何中一维、二维、三维之间的联系，让学生的想象、推理能力达到新高度。这样的课堂设计，让学生有独立思考的时间、有合作交流的空间、有探究发表的机会，使得学生的思维在交流中得以彰显。此环节沟通了线段与平面图形的联系、平面图形与立体图形之间的联系、立体图形与立体图形之间的联系、立体图形各要素之间的联系。

综上所述，在数学教学中，教师应于温故中知新，于联系中整合，于交流中彰显思维深度！

（责编 覃小慧）