追本溯源 深入拓展 让思维开启高阶模式
卢家杰




【摘要】数学运算教学不仅是学生计算技能的培养,还应重视运算中高阶思维能力的发展。然而在小学第一学段教师常常只重视夯实计算技能,忽略运算教学中高阶思维的渗透。本文结合目前指向高阶思维的运算教学现状,从目标维、资源维、活动维三个角度来阐述高阶思维应用于第一学段数学运算教学的策略和实践。
【关键词】第一学段、高阶思维、运算能力、数学教学
《义务教育数学课程标准(2011年版)》正式将“运算能力”列为十大数学核心概念词之一。随着当今社会高速发展,各行各业大量数据信息瞬息万变,我们的人工智能足以代替人脑进行大量的低阶思维工作,如接收信息、存储信息、操作计算等等。而我们培养的学生,不该停留在低阶思维水平,而是具有在复杂多样的环境中发展观察、分类、思考、推理、探究、质疑、创新、制定解决方案等高阶思维能力。数学运算教学不仅是学生计算技能的培养,还应重视运算中高阶思维能力的发展。只有这样,我们培养的学生才能适应高速发展的学习、工作和生活。
一、高阶思维的内涵
根据心理学家布卢姆的教学目标分类,学生的数学思维可以分为六个层次,其中“分析”、“评价”和“创造”属于高阶思维。本文所讨论的运算中高阶思维主要是指学生在熟练掌握并运用数学的基本定义,基本法则和基本公式能正确进行计算的基础上,能对运算结果进行反思和判断,还能够灵活运用类比推理,迁移方法解决问题或者多种方法解决问题,实现运算方法的优化。
二、调查与分析
既然运算教学中高阶思维能力有如此重要的价值,那么在现实的课堂教学中教师是否有足够的重视呢?有没有将运算中高阶思维能力的培养落实到一线课堂?因此笔者设计相关问卷,进行调查。
(一)调查过程
1.调查时间:在2020年5月10日设计调查问卷,2020年5月20日下发问卷,进行问卷调查。
2.调查对象:本人所在的学校处于城乡结合部,是一所刚成立五年的新学校。选取三年级两个班级,共77人进行问卷调查。
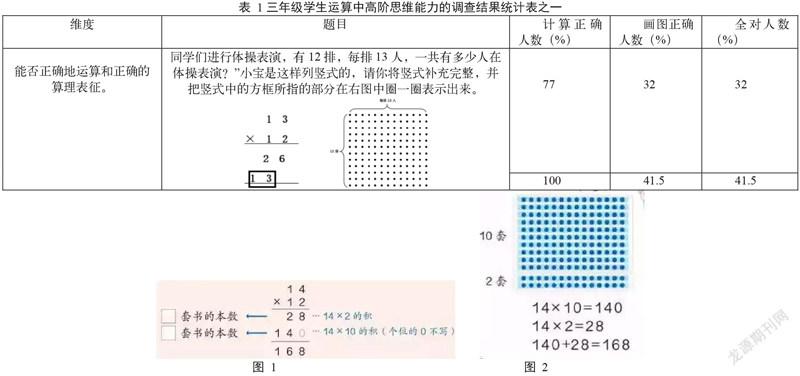
3.调查内容:从“能否正确地运算和正确的算理表征”、“灵活选用算法,运算方法和过程是否简便”、“能否对运算结果进行检查和判断”、“能否进行推理计算”4个维度出发,设计一份指向高阶思维的运算能力调查问卷。
4.调查结果:共下发问卷77份,有效收回问卷共77份。从调查结果显示,小学第一学段运算中高阶思维的培养并没有得到很好的落实。
(二)分析与思考
統计分析问卷的数据,并结合后续学生访谈情况,发现学生指向高阶思维的运算能力主要存在以下几方面的问题。
1.算理的理解浮于浅层
学生能否正确地运算,并正确地表征算理,是运算中高阶思维的重要基础。每一位学生都能正确地计算,但是只有41.5%的学生在点子图中正确地表征出这道题的算理。而回归课本教材内容(如图1和图2),发现相同的算理知识点在人教版小学数学三年级下册第46页是借助点子图作为例题在课堂上重点讲解过的,并非学生们第一次遇到。由此可见,教师将运算教学的重点(甚至全部)落到了如何快速、正确地计算出结果。而对应的运算算理和计算本质被忽略。
如果题目中遇到应用基础算理来解决问题或者利用算理推理解决更加复杂的计算问题时,有部分学生就会不知所措,无从下手。而对于基础算理扎实的学生来说,这一类题目就非常简单了。
2.算法的选择存在定势
由于二、三年级竖式运算的机械性训练或者多重外在引导等因素(如老师、家长反复强调列竖式计算能保障计算结果正确),“列竖式计算”成为大多数学生运算时的最佳选择,甚至是唯一选择。学生在运算过程中未能灵活使用估算、心算、简便运算解决问题,大多数学生也缺乏对运算结果进行反思和判断的能力,算法选择存在定势。
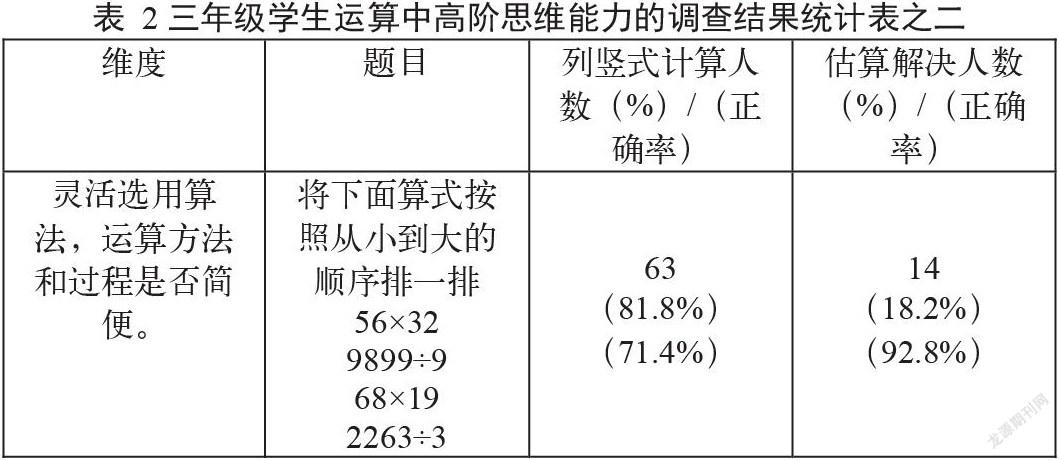
学生能否灵活选用算法,方法和过程是否简便,这是运算中高阶思维的重要属性之一。接受调查的学生有81.8%采用列竖式的方法得出每个算式的结果,然后再进行大小比较。只有18.2%是通过估算的方法得出近似结果,再进行大小比较。比较正确率,明显选用估算解决的正确率更高。访谈后了解到学生选用每一个算式都列竖式计算出正确结果的原因是在于“怕估算思路不清,导致估算的结果错误。用列竖式得到结果,然后进行大小比较更准确,也更加放心。但是偶尔列竖式也会出现计算错误。”
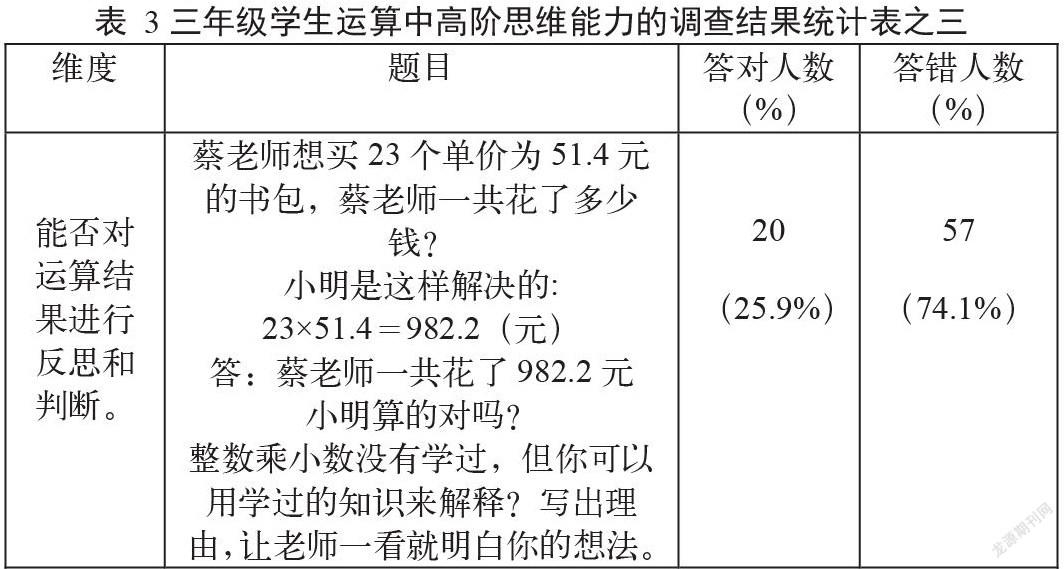
不同于以往的单一试题求“蔡老师一共花了多少钱?”,而是给了一位同学的解答方法,让学生来判断他算得对吗,其实就是在考察学生对运算的结果是否有反思和判断的能力。由于整数乘小数没有学过,题目提示要求用已经学过的知识来解释说明理由。要解决这道题,用笔算和口算都显得过于复杂,但是用估算就容易许多。将23、51.4分别估小为20和50,估小后相乘也需要1000元,实际花的钱肯定大于1000元,也大于982.2元,所以小明算错了。
调查发现,这道题只有25.9%的学生做对了,翻阅这些同学的解题方法,发现将近90%的学生是用了估算的方法,剩余10%是将51.4元拆成51元和4角,也成功得解决了这道题。但是有74.1%的同学做错了,其中有尝试列竖式计算的,还有不少同学这道题甚至是一片空白。
3.结构的领会过于片面
指向高阶思维培养的运算教学,不仅只是计算技能的获取,更重要的是利用推理迁移方法发展逻辑思维能力,实现运算能力的深层次和更高水平的发展。
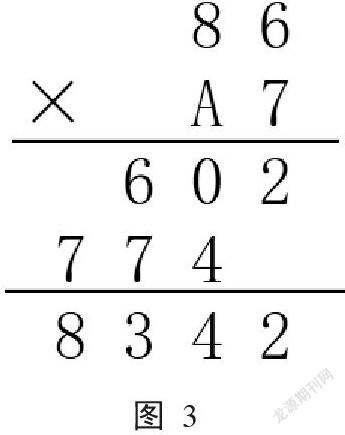
据统计这道题错误率不高只有9.9%。但通过后续访谈发现,学生们的解题方法非常多样。有85%的学生是从A到底是多少来入手考虑。只要知道A是多少,那么86×A7=( )自然就转化为两位数乘两位数的计算。由于还没有学过除数是两位数的除法,要知道A是多少,大部分学生采用代入一位数字试一试的方法,直到试对了为止。有从1开始代入,直到试到9。有的学生观察数字特点发现,774与860(即86×10)非常接近,于是他从A是9开始代入,结果只试了一次就发现A的真实数值。还有同学从尾数入手,6×( )的个位是4呢?想到四六二十四和六九五十四,将4和9分别代入验证得到A是9。解决了A是多少,只需要列竖式就能得到正确的结果。
还有5%的学生,他们表示不需要知道A是多少,现在A 在十位上,意义就是A个十。根据已学过的算理和算法,只需利用竖式就能轻松推理解决,而且用时较少。(如图3)根据学生的解答情况和后续的访谈,了解到学生利用算理和算法,推理解决问题的能力只在个别同学身上有所展现。
(三)归因分析
为什么三年级学生数学运算中的高阶思维能力如此单薄呢?反思现实的第一学段数学运算教学,原因不外乎以下三个方面:
——运算中的高阶思维能力的培养,需要教师有正确的运算观和深入的本质理解。但事实上教师对数学运算的理解往往还不够透彻,导致在运算教学中重结果而轻过程。学生们也因此进行超量重复的口算、笔算训练,却对于数与运算意义、运算规律等算理的理解常常被忽视。
——运算中的高阶思维能力的培养,需要教师用系统化的思维去整合碎片化的知识。在低段的数学运算教学中有不少碎片化或者重复的知识。没有进行重组和结构化的知识,显得过于琐碎,也增加学习过程中的无趣,减退学生学习的积极性。
——运算中的高阶思维能力的培养,需要经历归纳、猜想、验证等过程。教师在授课中不但要让学生明白“是什么”,而且要让他们明白“为什么”。可惜的是,教师常常在教学过程中只告诉学生“是什么”,却不肯花时间放手让学生探究“为什么”。
综上,计算技能的掌握和提高是立竿见影的,而高阶思维能力的提高是一步一步慢慢渗入。因此在小学第一学段运算教学应重视学生高阶思维能力的发展,重视算理的理解,鼓励算法的推理迁移运用,让学生经历归纳、猜想、验证等活动,获取高阶思维能力。
三、策略与实践
由于高阶思维能力是需要慢慢渗透,我们需要从第一学段开始就关注学生运算的高阶思维能力的培养。学生能够正确地理解运算的算理,主动探索多样化的算法并寻求简洁合理的运算途径来解决问题。会运用推理,利用知识方法的迁移,创新地解决问题。
将高阶思维应用于第一学段运算教学时,可以从以下三个维度进行尝试:
(一)目标维:指向高阶思维的教学定位
只有在教学目标中,高阶思维能力的目标不缺位,教师心里有意识,教学行为才会有跟进,学生运算高阶思维能力培养的落实才会实现。因此在以往粗略的每课时教学目标基础上进行目标细化,并且根据教学内容额外增加高阶目标预设。
以人教版小学数学三年级上册《万以内的加法和减法(一)》几百几十加减几百几十 (P14)为例:
这样,将原来的粗略目标进行细化,将每个目标都落实到位,同时增加高阶目标预设。教师在完成基础目标后,进行高阶目标的落实,真正做到心中有数。
(二)资源维:指向高阶思维的学习载体
教学资源是学习数学的重要载体,指向高阶思维培养的小学运算教学,教学资源的选择和编排就十分重要的。教学是否成功,主要取决于教师在课堂上提供什么样的学习材料。在教学中,我们可以通过资源挖掘、整合和拓展等策略,落实运算教学高阶思维能力的培养。
挖掘:一道简单的计算题背后有多少的思维含量,是需要我们教师去挖掘的。例如计算46+27,如果教师只是要求学生计算出正确的计算结果73,那么学生的思维训练也就止步于此。教师可以請学生将这道简单的计算题,改编成为选择题。选项中除了正确选项73之外,这个选择题的其他选项可以是什么答案呢?请同学来说一说自己的选项,并说明理由。有同学补充“63”,原因是自己会经常忘记进位。还有同学补充“19”,原因是审题不仔细将加法看成减法进行计算了。明明知道答案的计算题,逆向追问思考,可以蕴含多种不同的思路。
整合:根据学情出发,用系统化的思维去整合教学内容,从碎片化,繁琐,无趣的知识点走向整体设计,逐步递进的单元主题。如在人教版小学数学三年级上册第二单元《万以内数的加减法(一)》和第四单元《万以内的加减法(二)》,这两个单元的算理相同而且教学时间安排较近,我们考虑将这两个单元知识的教学进行整合。(如图4)
拓展:从教材整体出发,适时补充。不仅要教这一课时的知识内容,而且要将这个知识点放到整个小学数学教材中加以通盘考虑,加强知识间的纵向联系。将单元知识整合,多余的课时我们就用来进行拓展。在学习两位数加减两位数的口算后出示以下两组题,要求学生正确计算结果并仔细观察,写一写:你还发现什么了?
题组1:
30+40= 45+74= 10+35=
40+30= 74+45= 35+10=
题组2:
30+80+20= 18+24+76= 16+40+60=
30+(80+20)= 18+(24+76)= 16+(40+60)=
这两题组,除了要求学生正确计算结果外,还需要学生观察算式的特征。其实仔细观察不难发现,题组1中上下两题加数交换了位置,但是和不变。题组2上下两题加数的数字不变,添加小括号后改变了计算先后顺序,得到的和不变,而且计算过程也更加方便。这两组题的思维本质就是四年级学习的加法交换律和加法结合律。但我们在三年级的时候已经在慢慢渗透,当学生遇到34+54⚪54+34,18+24+76⚪ 18+(24+76)这类比较大小的题目时不需要去计算出每个算式的具体结果,只要观察数字和符号特点就能比较出大小,既节省了做题时间,又提高正确率。
(一)活动维:指向高阶思维的学习活动
蕴含高阶思维的学习活动是较受学生喜爱的学习方式。已经有一些研究表明,有趣的项目式学习有利于发展学生的高阶思维能力。
2020年一场突如其来的新冠肺炎疫情,把全国的孩子都困在了家里。各个学校积极相应“停课不停学”教育教学模式,纷纷根据各学科特征开展项目式学习。本校三年级数学组老师根据三年级上册已学知识和疫情相关信息相结合开展项目式学习。三年级上册,学生刚刚学了“万以内的加法和减法”“倍的认识”,结合每天新闻发布各地区的疫情实时数据,我们引导孩子编写加减法应用题一两道,还有“倍”、“和倍”或“差倍”的应用题一道。要求附上相关新闻报导的图片,保证数据的准确性,同学们在钉钉班级圈进行展示,班里同学可以挑选自己感兴趣的题目进行评论解答。如:1月22日,我国累计确诊新冠肺炎患者644人,1月23日累计确诊830人,新增多少人?1月22日累计某地区死亡人15人,一星期后的1月28日累计死亡人数高达143人,1月28日累计死亡人数大约是1月23日的几倍?并分析死亡人数不断上涨背后的原因。
生活中的数学有非常丰富的材料,通过分析情景化的数学运算问题,给学生提供了一个锻炼高阶思维的平台。
综上,在运算教学中将低阶思维作为构建高阶思维发展的抓手和基底,在正确理解算理和算法的基础上,还能灵活选用合理的算法,抛开固有的定势。能够会运用推理,利用知识方法的迁移,创新地解决问题。指向高阶思维的运算教学,需要教师拥有基础和高阶相结合的教学定位,需要教师挖掘、整合、拓展教学资源,需要教师开展有深度的计算教学活动。
参考文献
[1] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
[2] 曹培英.跨域断层,走出误区:“数学课程标准”核心词的实践解读之七:推理能力(上)[J].小学数学教师,2014(7/8):87-94.
[3] 朱茵羽.指向核心素养的数学高阶思维的培养策略.数学教学通讯,2020(2上).
[4] 林琳,沈书生,李艺.谈设计思维发展高阶思维何以可能——基于皮亚杰发生认识论视角[J].电化教育研究,2019(8):1-8
[5] 郭颖.浅谈小学数学口算、估算、笔算三者之间的辩证关系[J].数学学习与研究,2018(19):112.

