优化的分数阶GM(1,1)模型在桥梁线形控制中的应用

洪晓江，张雪松，郭 宁，李鸿鸣

(1. 西昌学院 土木与水利工程学院,四川 西昌 615000； 2. 重庆交通大学 土木工程学院, 重庆 400074；3. 成都理工大学 地质灾害防治与地质环境保护国家重点实验室, 四川 成都 610059)

0 引 言

预拱度是大跨度悬臂桥梁施工线形监控中的重要调节参数，通过提高预拱度的预测精度能保证施工阶段和成桥状态的线形尽可能地达到设计要求。随着桥梁跨度的逐渐增大和施工方法的不断更新，预拱度控制不仅显得尤为重要，也对其精度、稳定性等各项性能指标提出了更高的要求。从现代控制理论角度出发，大跨径刚构桥梁线形监控是一个非线性和时变性的不确定性系统问题。控制方法正逐步从传统的建模计算、人工测量、反馈分阶段控制转变为智能化的监测预警预测一体化的自适应控制。计算理论已由单纯的力学问题演变为力学、数学、计算机和信息技术等多学科的综合问题。

目前常用的预拱度预测方法主要分为两大类，第1类是基于大数据、多样本的概率论与随机过程模型，以卡尔曼滤波[1]、神经网络法[2]为代表；第2类基于少数据、贫信息的控制论模型，以灰色模型理论为代表。大跨径刚构桥梁悬臂施工具有节段数量有限、线形状态受施工参数影响复杂多变的特点，灰色预测理论正好适用于解决此类问题。灰色理论自20世纪80年代诞生以来，已经成功运用于军、工、农、医、交通等诸多领域，在大跨径刚构桥梁施工监控方面也取得了许多成果。张永水等[3]首次将GM(1,1)引入刚构桥梁施工监控，验证了其可行性。为了弥补传统GM(1,1)的不足和提高预测精度，许多学者做了相关研究；李自林等[4]在连续刚构桥梁施工监控中利用残差序列建立了残差GM(1,1)模型，预测结果显示残差GM(1,1)优于传统GM(1,1)；包仪军等[5]针对GM(1,1)的背景值构造方法进行了改进，建立了一个效果较好且稳定的悬臂桥梁线形预测模型；另外，姚荣等[6-7]均将GM(2,1)与GM(1,1)做了仿真对比分析，结论各异，说明了原始挠度数据的趋势关系特性应与合理的阶数相匹配才能避免出现病态预测，进而提高预测效果的稳定性。

综上所述，整数阶阶数的灰色模型在大跨度桥梁施工监控领域中已得到了广泛的应用，但是基于分数阶阶数的灰色模型在该领域的研究和应用几乎没有。近年来，分数阶灰色模型得到很高的关注度，它是对整数阶灰色模型的拓展，有其特有的优势。孟伟[8]研究表明：相比整数阶灰色模型，分数阶灰色模型不仅能满足新信息优先原则，而且在样本数量达到最优时预测具有稳定性好、扰动小和精度高的特点。鉴于此，笔者将分数阶算子GM(1,1)引入大跨径刚构桥梁施工监控，并对模型背景值进行优化，得到改进的分数阶GM(1,1)预测模型。通过实例验证新模型的拟合和预测效果，以期有一定的实际应用价值。

1 基于牛顿插值的分数阶GM(1,1)模型

1.1 分数阶拓展算子的GM(1,1)模型

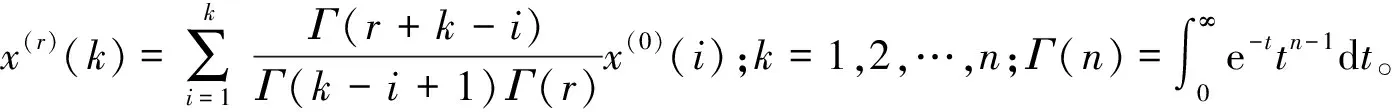
分数阶GM(1,1)模型的差分形式为：

x(r-1)(k)+az(r)(k)=b

(1)

式中：a为模型的发展系数；b为灰色作用量。背景值z(r)(k+1)的常用构造公式为：

(2)

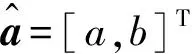
(3)

当r=1时，由式(1)可得到x(0)(k)+az(1)(k)=b，模型变为传统的GM(1,1)。

1.2 基于牛顿差值的分数阶GM(1,1)模型

实际上，背景值z(r)(k+1)的精确解为：

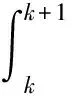
(4)

而式(2)是根据牛顿-柯特斯(Newton-Cotes)求积公式得到的梯形积分数值解，该公式只有1次代数精度。大量文献已证明该近似计算方法会影响预测精度[9-11]。另外，经计算验证，若采用具有3次代数精度的辛普森公式进行一次牛顿差值计算，所得背景值构造公式与式(2)相同，并未真正意义上进行优化。在保证求积公式稳定及收敛的前提下，为了进一步提高代数精度的次数，减小逼近误差，选用具有3次代数精度的求积公式对式(4)进行二次牛顿插值求解，从而得到一个精度较高的分数阶灰色模型背景值构造公式。

根据牛顿-科特斯数值积分计算公式，具有3次代数精度的背景值构造公式为：

(5)

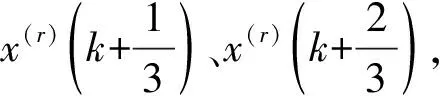
Nk(t)=x(r)(k)+x(r)[k,k+1]×(t-k)+x(r)[k,k+1,k+2]×(t-k)×[t-(k+1)]

(6)

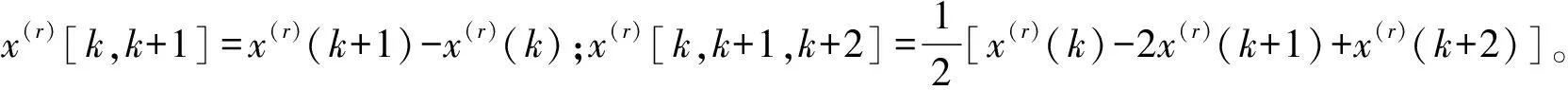
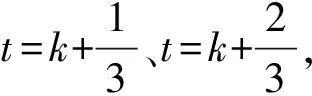
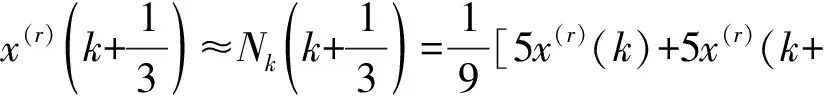
(7)

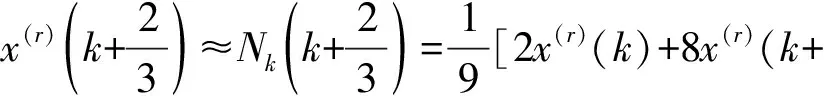
(8)

将式(7)和式(8)代入式(5)，可得k=1,2,…,n-2 时的背景值构造公式为：

(9)

而计算z(r)(n)应以最后3个节点n-2、n-1和n进行插值计算，同理可得：

(10)

综上所述，可得到基于二次牛顿插值的分数阶GM(1,1)模型，形式为：

x(r-1)(k)+az(r)(k)=b

(11)

其中：

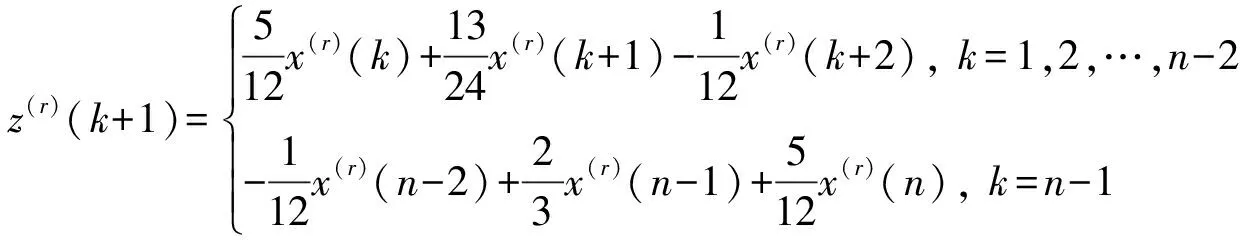
(12)

1.3 最优分数阶的算法步骤

阶数是分数阶灰色模型提高精度的关键因素。最优阶数r的求解以最小平均相对误差为优化指标，优化公式为：

(13)

以自适应变异粒子群优化算法(简称PSO)[12-13]搜索最优阶数r。该算法不仅计算简洁便于实现，且具有全局收敛性能，主要流程为：

Step 1初始化参数。δ为给定的收敛值，gbest设置为最佳粒子位置，取粒子初始位置pbest=r=1，此时模型为GM(1,1)。

Step 2根据式(13)计算pbest=r时分数阶模型的f(r)。当|f(pbest)-f(gbest)|<δ时，转向Step 4；否则，执行Step 3。

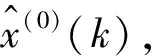
Step 4输出收敛准则下的r值，即为分数阶灰色模型的最优阶数。

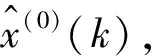
2 连续刚构桥线形监控实例

重庆石柱至黔江高速公路上在建的里头河大桥主桥是跨径为70 m+130 m+70 m的预应力混凝土变截面连续刚构桥，采用悬臂浇筑法施工。节段划分为：0号块，1号～16号悬臂浇筑段，合龙段。以3# 墩向中跨部分悬臂浇筑线形控制为例，其向跨中侧悬臂浇筑节段尺寸如图1。为了保障顺利合龙以及成桥后桥面线形良好，需通过有限元软件模拟仿真分析和现场监测相结合的方法，对主梁施工过程中的预拱度变化状态进行有效地计算、监测、分析和预测，已达到自适应控制。

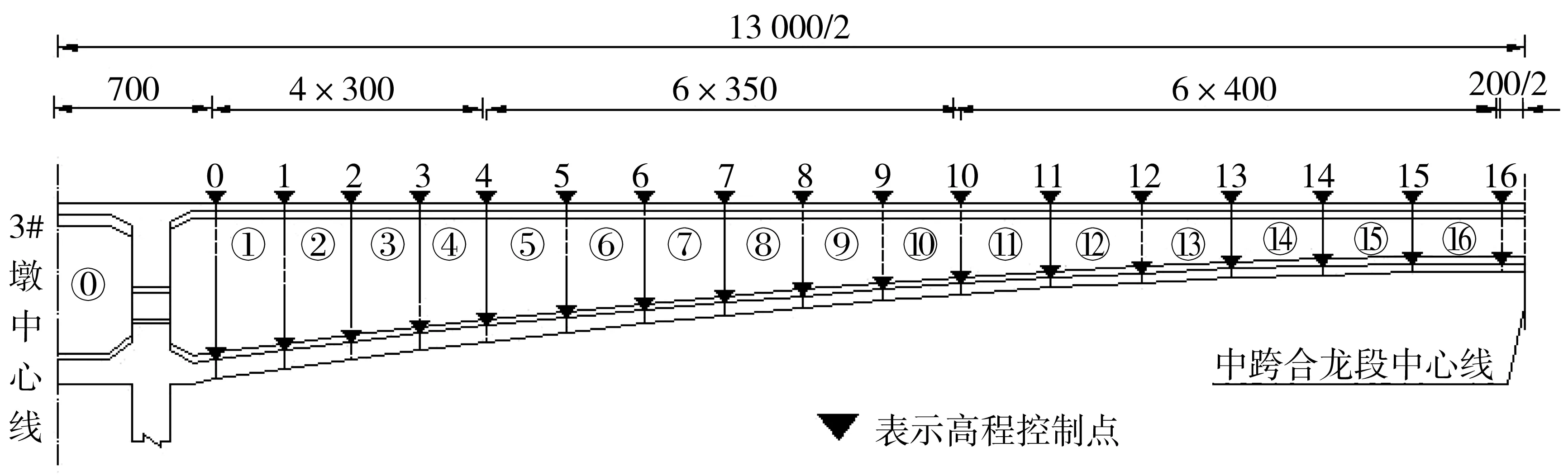
图1 悬臂浇筑节段(单位：cm)Fig. 1 Cantilever casting section

首先，利用有限元软件建立力学计算模型，如图2。通过对各工况进行正装分析，计算各施工节段的应力和位移等参数，模型包含156个单元。其次，在各个节段施工时，在距离节段前10 cm布置高程测试截面，如图1。每个截面布置5个高程控制点，用于测试实际预拱度，如图2。最后，通过对已浇筑节段预拱度的理论值、实测值进行对比分析，寻找偏差原因，从而调整参数，预测下一节段的预拱度。

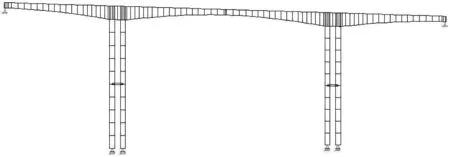
图2 力学计算模型Fig. 2 Mechanical calculation model

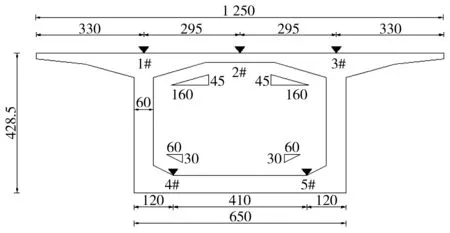
图3 横断面控制点布置(单位：cm)Fig. 3 Layout of cross section control points

限于篇幅，表1列出了4号～8号节段的高程控制横断面上的2# 监测点在预应力张拉后的预拱度监测数据。从数据变化可推断出，计算参数取值误差、测量误差以及现场施工环境多变等原因导致了各节段实测预拱度值均大于理论值。

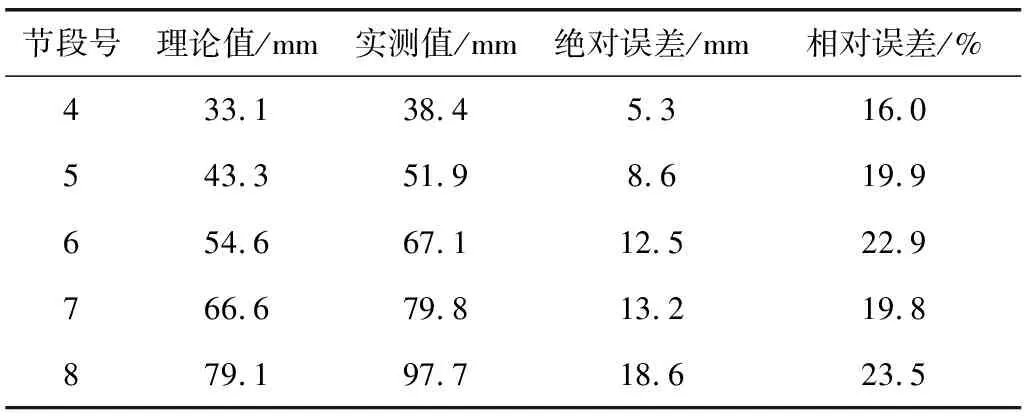
表1 部分节段预拱度监测数据Table 1 Partial segment camber monitoring data

3 模型预测及对比分析

3.1 基于牛顿差值的分数阶GM(1,1)模型应用

从样本数量角度出发，不少于4个数据序列建立灰色模型进行线形监控预测可进一步减小预测误差[14]。因此，选取表1中4号～8号节段的预拱度监测数据为原始样本数据建立基于二次牛顿插值的分数阶GM(1,1)。

首先，以4号～8号节段张拉后预拱度实测值与理论值的差值为模型原始序列X(0)，则：

X(0)=(5.3,8.6,12.5,13.2,18.6)

通过PSO算法，以最小平均相对误差为指标，搜索得最优阶数r=0.54，此时构造的背景值为：

Z(0.54)=[9.223 1,16.355 5,23.863 1,33.460 8]

最后，经过累减生成的原始序列模拟值为：

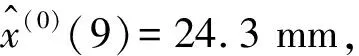
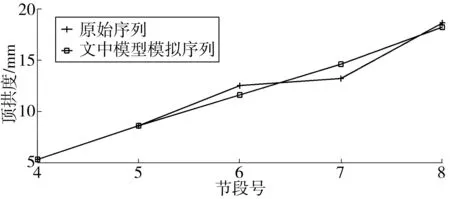
图4 原始序列与模拟序列对比Fig. 4 Comparison of original sequence and simulated sequence

3.2 预测精度对比分析

为了检验模型在连续刚构桥梁预拱度预测的精度，将文中模型、传统GM(1,1)以及分数阶GM(1,1)分别用于模拟4号～8号节段的预拱度数据，并用误差检验的残差ε(k)、相对误差Δk以及平均相对误差Δ共3个指标进行精度评定，结果如表2。

预测结果可见，分数阶GM (1,1)预测得到的各个值的残差、相对误差均有所减小。更重要的是，分数阶GM(1,1)的预测平均相对误差为6.0%，相比传统的GM(1,1)模型减少了6.1%，充分说明了对GM(1,1)阶数的优化可以改善预测效果。在分数阶模型处理中，文中模型将背景值参数构造方法的代数精度进一步提高，增强了原始序列的平滑效果，弱化了极端值的影响，使平均相对误差减小到3.1%。

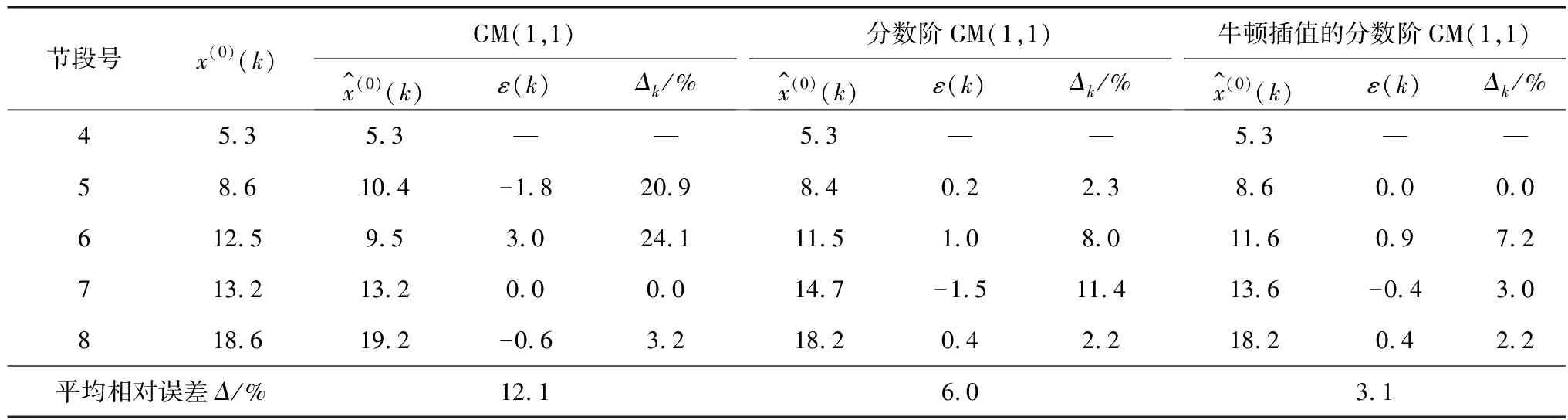
表2 不同灰色模型预测精度比较Table 2 Comparison of prediction accuracy of different grey models

4 结 论

针对传统灰色预测模型用于大跨径刚构桥梁会出现过拟合现象和预测精度不高的问题，笔者将分数阶算子GM(1,1)模型引入大跨度桥梁预拱度预测，并建立了一种基于牛顿二次插值的分数阶GM(1,1)新模型，实现了对传统GM(1,1)模型的阶数和背景值的双重优化。得出以下结论：

1)与传统的GM(1,1)相比，分数阶GM(1,1)模型具有自适应拟合和新信息优先的优点。在最优分数阶状态下，所得到的模型的平均相对误差最小。

2)将传统的GM(1,1)的阶数由整数拓展到分数，可以改善模型的预测精度；背景值的构造由传统的梯形求积公式优化为具有三次代数精度的二次牛顿插值求积公式，增强了原始序列的平滑效果，弱化了极端值对灰色预测模型精度的影响。

3)工程实例应用表明，将分数阶GM(1,1)引入大跨径刚构桥梁施工监控是可行的，优化的分数阶GM(1,1)可以进一步预测精度较高，对于同类型的桥梁施工控制有一定的参考价值。