基于全局优化算法的增程式电动汽车模糊控制策略

牛礼民，张泉泉，朱奋田，宗发新，郑飞宇

(1. 安徽工业大学 机械工程学院，安徽 马鞍山 243032； 2. 国网固镇县有限公司，安徽 蚌埠233700)

0 引 言

在传统串联型混合动力汽车的基础上，增程式电动汽车(extended-range electric vehicle，EREV)改变能量的分配方式。增程器(发动机/发电机)和动力电池以电气连接的方式提供整车动力，同时保持在各自最优效率区间工作。能量管理策略是混合动力汽车整车控制的核心[1]，当前EREV能量管理策略主要分为规则型[2-3]、优化型[4]和智能型[5]。规则型能量管理策略开发周期短，实车性强，但整车燃油经济性较低；优化型能量管理策略控制系统复杂，控制动力部件在其最优经济区间工作，计算量大、耗时长，开发周期较长；智能型能量管理策略利用优化算法协调多动力源间能量分配，且控制精度高。其中，模糊控制策略因其自适应能力强、运算速度快，且不需要建立精确的控制系统等特点广泛应用于混合动力汽车控制系统[6]。但由于行驶路况的复杂及驾驶员驾驶操作意图的随机性较大，仅依据工程经验所制定的模糊控制规则库难以协调不同动力源间的能量分配[7]，从而对驾驶舒适度及整车燃油消耗造成影响。

金辉等[8]根据动态规划最优性原理，提出了智能车起步过程的经济性车速规划方法，将优化后的车速和档位作为智能车启步依据，具有良好的节油特性；冯坚等[9]基于动态规划算法和路况的增程式电动车能耗分析；周美兰等[10]分析模糊控制策略在复合储能电源中的功率、锂电池SOC变化曲线以及储能系统的能量流图，相对于逻辑门限和锂电池单独驱动，模糊控制策略能降低锂电池电流，有效回收制动能量；王赛等[11]以燃料电池汽车结合动力电池模组的方式，提出了基于微小变量模糊逻辑控制的燃料电池补偿动力电池放电的能量管理控制策略模型；杨小龙等[12]提出了基于多因素输入模糊控制的再生制动策略，将机械制动效能因子引入模糊控制器，以此优化再生制动力分配比例，完成能量回收；臧怀泉等[13]提出了一种基于禁忌搜索-免疫粒子群算法的整车模糊能量管理策略，利用免疫粒子群算法对模糊控制器参数进行离线优化；吴晓刚等[14]利用粒子群算法对模糊控制中的隶属度函数进行优化，降低电池组SOC变化，在一定程度上将电池SOC控制在比较合理的范围。

现有模糊控制策略采用基于工程经验作为模糊控制规则库制定依据，其中多采用引入影响因子作为模糊控制额外输入或利用优化算法对隶属度参数进行优化，全局优化能力较弱，且容易出现局部最优的情况，从而导致整车经济性下降。针对于此，笔者提出一种基于全局优化的EREV模糊控制能量管理策略，分析并提取动态规划算法在不同路况下的能量分配，作为制定模糊控制规则库的依据，同时利用粒子群算法优化控制策略及隶属度函数参数，实现多动力源间能量的合理分配；最后搭建MATLAB/Simulink模糊控制策略模型，并经硬件在环测试验证所提策略在不同工况下的整车控制效果。

1 全局优化策略

根据需求功率来分配增程器和动力电池间的能量，EREV在传统串联混合动力汽车的基础上增加了多种行车模式，以面对日益复杂的行驶工况和不同需求的驾驶意图等情况。整车能量管理策略根据不同驾驶信息和动力部件状态等，协调优化不同能源间能量分配，使各部件在最优效率区间工作，在满足动力性条件下节能减排。

在复杂多变的驾驶环境中，通过制定动力电池电量低阈值作为增程器的开启条件，显然不能满足当前能量管理趋势。全局优化控制策略通过实时车辆信息协调整车能量分配，根据需求功率和动力电池发电能力判断增程器的开启及输出量，有助于延长动力电池使用寿命、降低整车燃油消耗，且当动力电池进入低阈值时能维持动力电池电量状态。

图1为全局优化控制策略示意，由图1可知，全局优化策略是在模糊控制策略的基础上添加了动态规划模块和粒子群算法模块，利用动态规划算法提取相关能量分配规则，并结合工程经验为模糊控制策略提供规则库制定依据；利用粒子群算法优化部分控制策略及模糊隶属度函数参数，使得模糊控制策略具有全局优化性。

2 动态规划的规则提取

在模糊控制中，模糊控制规则库的指定大多取决于工程经验，缺乏全局优化特性，不适应当前复杂多变的工况。动态规划是在已知工况的条件下将时间工况离散化，转化为过阶段决策问题，逆向求解至初始阶段以获得全局最优能量分配序列点。基于此，利用动态规划优化算法对不同工况进行仿真，分析并提取不同工况下的能量分配规则，使得模糊控制策略更具有全局优化性，从而提高整车燃油经济性、排放性。

2.1 增程式电动汽车数学模型

在获取动态规划规则前，根据EREV动力源部件MAP图建立动力学简化数学模型，以减少动态规划算法在迭代过程中的复杂度。在增程式电动汽车行驶过程中，增程器和动力电池以电气连接的方式将能量传递给驱动电机，驱动电机将接收到的电功率解耦成传动系统中所需求的转矩、转速。

作为EREV唯一驱动源动力部件，驱动电机实现机械和电气间的功率转换。当整车需求功率为负值时，将机械能转化为电能存储在动力电池中；当需求功率为正值时，将电能转化为机械能驱动车轮行驶。本节通过增程器最优效率曲线和动力电池模型进行描述。

1)增程式电动汽车大多以发动机最优效率曲线作为增程器工作区间，忽略了发电机工作时的机械效率问题，导致增程器整体工作效率变低。增程器以电气连接的形式对外输出能量，不用考虑转矩、转速限制，可以沿着当前转速下效率最高点进行发电。式(1)为增程器数学模型，在当前转速下，选取发动机与发电机最高发电效率作为发电工作点。图2为增程器最优效率曲线，通过最优效率曲线计算当前转速下增程器燃油消耗和转矩。

(1)

式中:ωfc-gc、Tfc-gc分别为发动机与发电机的转速、转矩；ηex、ηfc、ηgc分别为增程器、发动机和发电机的发电效率；Pex为增程器输出功率。

2)不考虑电池电化学过程，笔者将动力电池看成由理想的开路电压和1个内阻串联组成的等效电路[15]，其中电压、电阻只与动力电池的电量有关，如图3。

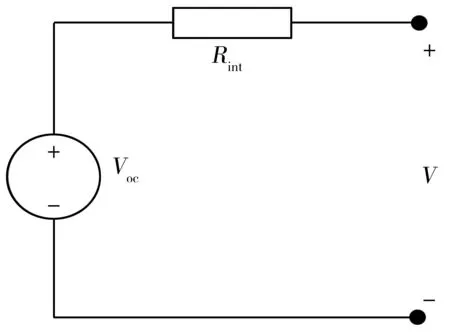
图3 动力电池等效电路Fig. 3 Power battery equivalent circuit

(2)

式(2)为动力电池等效电路电流与电池荷电状态计算公式，其中：Voc(t)为动力电池的开路电压；R为动力电池的等效电阻；Pess(t)为动力电池的功率，正值表示放电，负值表示充电；SOC为动力电池的荷电状态；Qess为动力电池容量。

2.2 动态规划算法的实现

动态规划算法(dynamic programming，DP)是一种基于贝尔曼最优性原理的用于求解多约束问题的优化方法，适用于EREV在固定工况下的能量管理问题进行求解，通过离线计算获得全局最优结果[16]。根据EREV在行驶工况中主要动力部件的能量转化过程，将已知工况、功率平衡方程、燃油经济性及动力部件约束条件等信息，应用到DP全局能量管理优化步骤中，如图4。动态规划算法求解步骤主要包括：信息初始化、离散系统变量、可行域求解、最优性求解。

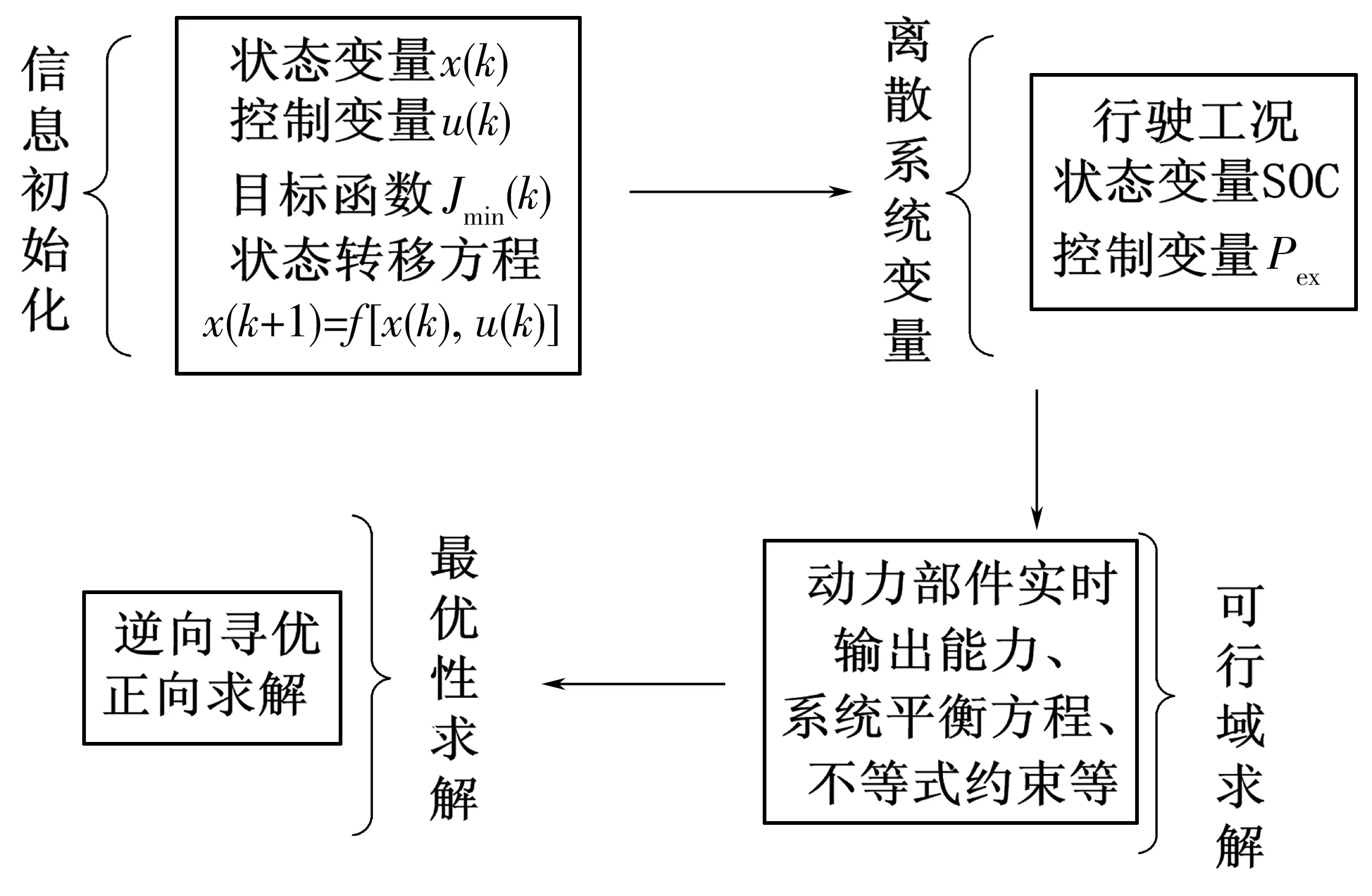
图4 动态规划算法求解步骤Fig. 4 The solution steps of dynamic programming algorithm

为了在不同工况下合理的使用动力电池中的电量，不至于出现过充、过放及瞬时功率激增等情况，以动力电池SOC值作为系统状态变量，增程器功率为控制变量，燃油经济性为目标函数，如式(3)：

(3)

式中：k=1, 2, …,N；N为已知行驶工况总步长；x(k)为动力电池SOC；u(k)为增程式输出功率；Jmin为整车燃油经济性。

由式(2)、式(3)可得：

SOC(k+1)=SOC(k)-

(4)

式中：Voc、Rint为动力电池电压、电阻，其值随SOC值变化；Qess为动力电池容量；Pex为增程器输出功率。

由图2可知，根据增程器最优效率曲线在发动机MAP图位置，可以求得增程器不同功率下的燃油消耗，以此作为求解DP过程中的目标函数。增程器功率-燃油消耗如图5。

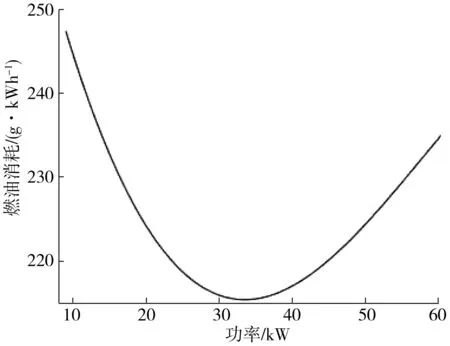
图5 增程器功率-燃油消耗Fig. 5 Extender power-fuel consumption diagram

在完成EREV到DP的信息初始化后，需要对变量进行离散化，包括已知工况、状态变量SOC和控制变量Pex。将已知工况划分为N个阶段，通常以1 s作为时间步长；系统控制变量f_ex以1 kW进行划分[fex_min:1:fex_max]；系统状态变量SOC以0.000 01划分为[SOC_min:0.000 01:SOC_max]。图6为DP离散变量点分布，在不同工况阶段N和状态变量SOC下，根据系统状态转移方程，通过比较不同控制变量所引起的目标函数值，选取最优的控制变量序列，并以此逆推至工况初始阶段；在给定的动力电池状态下，根据每个工况阶段所得到的最优控制变量和系统状态转移方程，得到基于DP的控制变量输出点。

图6 DP离散变量点Fig. 6 DP discrete variable points

在进行动态规划求解最优控制变量和目标函数时，由状态转移方程计算得到的系统状态变量，可能因未落在前一迭代步的SOC离散点上而造成误差。在提高系统状态变量离散精度的基础上，采用插值法使得在求解最优目标函数时，使得由控制变量计算得到的系统状态变量会落在上一个迭代步的SOC离散点上。在传统DP计算中，在每一个迭代步长内需要对当前迭代步中所有离散系统变量点进行计算，根据动力部件运行状态对迭代过程进行约束，从而计算出系统状态变量SOC有效运行区间，以减少程序运行时间，约束条件如式(5)：

(5)

式中：Pcharge_pwr、Pdischarge_pwr为不同SOC下动力电池充、放电功率限制值；ΔPex为增程器功率的变化率，ΔPex≤4 kW；tex为增程器开启时间，tex≥5 s；SOCmin、SOCmax分别为动力电池最小、最大极值。

由式(3)可知，在动态规划逆向求解初始迭代步第N步中，需要知道N+1步中由最优控制变量u(N)产生的目标函数JN+1，设定若在第N步中系统状态变量落在既定状态点上，则第N步的最优控制目标函数值为0，反之定义为INF。

2.3 DP优化分析

根据上文所述，在已知工况、动力电池SOC初始、结束值及相关约束条件下，分别对城市道路工况(urban dynamometer driving schedule，UDDS)和新欧洲循环驾驶工况(new european driving cycle，NEDC)进行动态规划算法计算，优化结果如图7、图8。

图7 UDDS工况动态规划结果Fig. 7 Dynamic programming results of UDDS working conditions

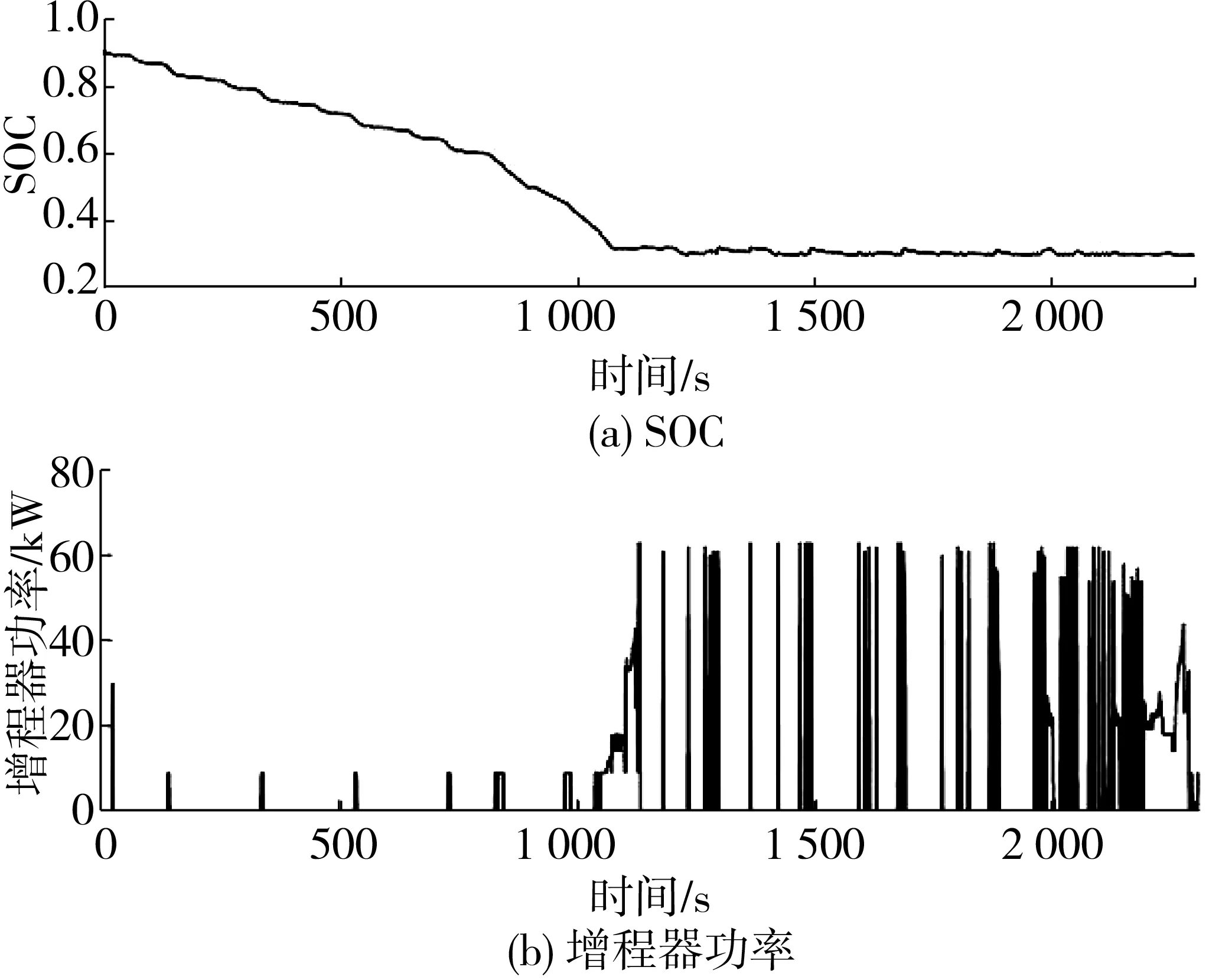
图8 NEDC工况动态规划结果Fig. 8 Dynamic programming results of NEDC working conditions

分析图7、图8可得出EREV在给定工况下能量分配规则：在动力电池电量充足的情况下，增程器只有在需求功率较高的情况下开启，同时并不对电池进行充电；而在动力电池电量较低时，增程器沿着最优效率曲线工作。因此在满足动力性条件下，减少了大电流对动力电池电量的快速消耗，从而增加了动力电池的使用寿命，又能使得增程器在高效点区间运行，提高整车燃油经济性。其中，在DP寻优结束后，SOC值均保持在相对稳定的状态，防止动力电池因过度放电对电池的损耗，便于下一次充电。

3 模糊控制策略

根据DP获取的能量分配规则，并结合相关工程经验作为模糊控制规则库的制定依据，使得在不同工况条件下，EREV能量管理系统能够根据动力电池荷电状态，智能化协调分配增程器和动力电池间功率输出，并且当仿真结束后保持SOC值在一定水平处。为了协调动力系统和模糊控制策略，利用粒子群算法优化部分控制策略及隶属度函数参数，获得更高的整车燃油经济性。

3.1 模糊控制系统

模糊控制系统主要包括输入、输出，模糊控制规则库，隶属度函数，模糊推理机制等。根据EREV整车功率流向，将整车需求功率Preq和动力电池SOC值作为模糊系统输入、增程器发电功率为Pfc系统输出，并采用以三角形类型为主的隶属度函数。将两个输入隶属度函数均划分为5个模糊子集；根据动态规划提取的增程器功率输出规律及增程器燃油效率经济区间，将输出隶属度函数划分为7个模糊子集，并且为不均匀分布，以提高模糊控制系统控制精度。模糊控制输入、输出隶属度函数如图9，表1为模糊控制规则库。模糊控制两个输入隶属度函数分别见图9(a)、图9(b)、输出隶属度函数见图9(c)，表1为模糊控制规则库，其中，NB、NS、M、VS、VB分别表示负大、负小、中、很小、很大。

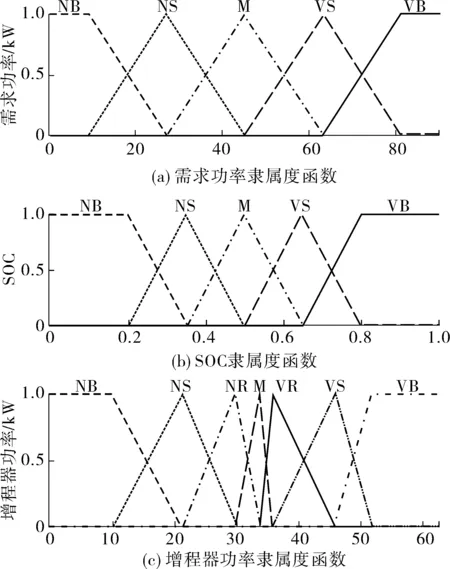
图9 模糊隶属度函数Fig. 9 Fuzzy membership function

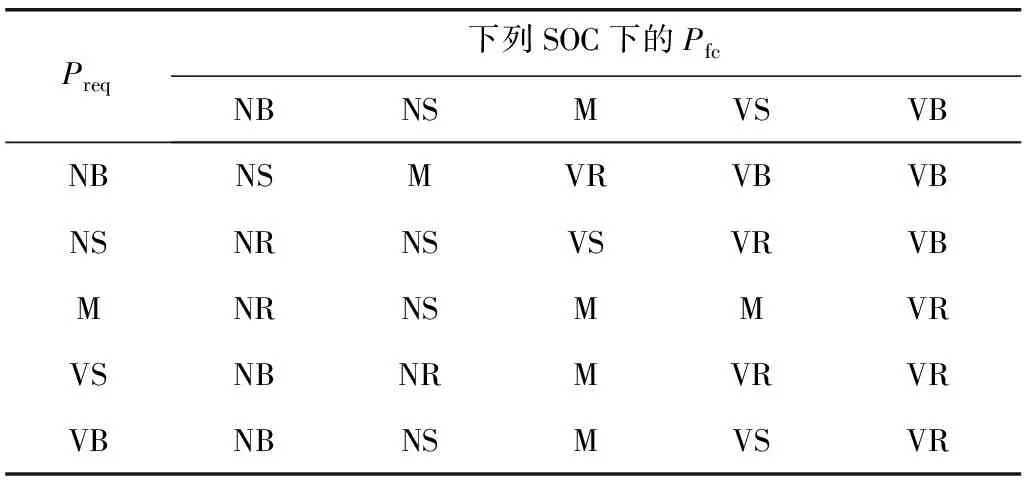
表1 模糊控制规则库Table 1 Fuzzy control rule base

由表1可知，模糊控制系统一共有25条规则，包含了整个变量输入区间，并采用Mamdani型推理机制进行模糊控制推理。

3.2 粒子群算法参数优化

EREV能量管理策略的目标是在满足动力性要求的基础上，要求控制策略根据动力部件实时状态协调功率分配。本节以燃油经济性及整车排放性为优化目标，利用粒子群算法离线优化整车动力及模糊隶属度函数参数，最后在ADVISOR汽车仿真软件中，将优化后的模糊控制策略用于实时仿真控制。

图10为粒子群参数优化简图，首先确定优化参数的数量及优化范围等，其中优化参数为34个、优化参数范围见表2；其次初始化优化参数，并带入EREV控制系统进行仿真，确定初代个体最佳粒子(pbest)、群体最佳粒子(gbest)；接着根据粒子速度、位置更新公式对粒子进行更新，再带入到控制系统进行仿真，并更新pbest、gbest。其中，速度更新公式中c1、c2为学习因子，取值为2；ω为惯性因子，取值为0.5；rand为0～1间的随机数；m为当前粒子数，m=1，2, …, 20。

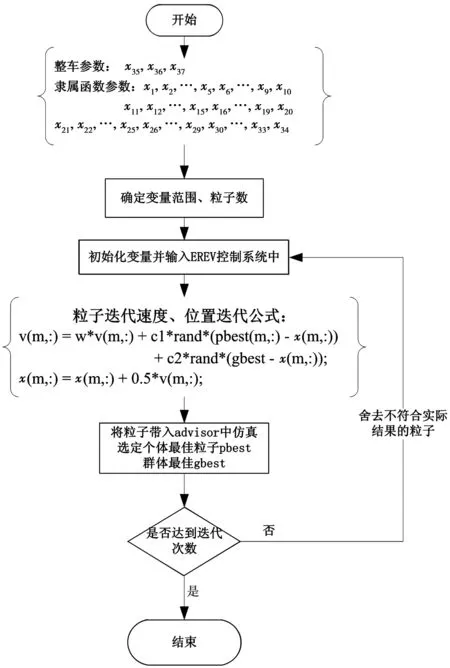
图10 粒子群参数优化简图Fig. 10 Particle swarm optimization diagram

粒子群优化参数变量及范围如表2，对于模糊隶属度函数分别以隶属子函数中心点和隶属子函数宽度的一半作为优化参数；对于控制策略参数以增程器最大、最小输出功率和动力电池SOC低阈值为优化参数。

表2 粒子群优化参数及范围Table 2 Particle swarm optimization parameters and range

在MATLAB/Simulink中建立EREV模糊控制策略模型，嵌入到ADVISOR控制模块中进行仿真，并根据整车燃油消耗及排放作为优化适应度目标函数，以此在迭代中不断地更新个体及群体最优值。

4 仿真结果

在MATLAB/Simulink中建立全局优化控制策略整车控制模型，并选取包含城市拥堵、郊区、高速等5种路段作为组合工况，分别为FTP(邦联认证瞬态循环工况)、1015(十十五循环工况)、UDDS、NEDC和HWFET(高速公路燃油经济性循环工况)，利用粒子群算法对部分控制策略及隶属度函数参数进行全局搜索优化。其中控制策略参数3个、隶属度函数参数34个，共迭代15次，初始种群粒子数为20，组合工况如图11。

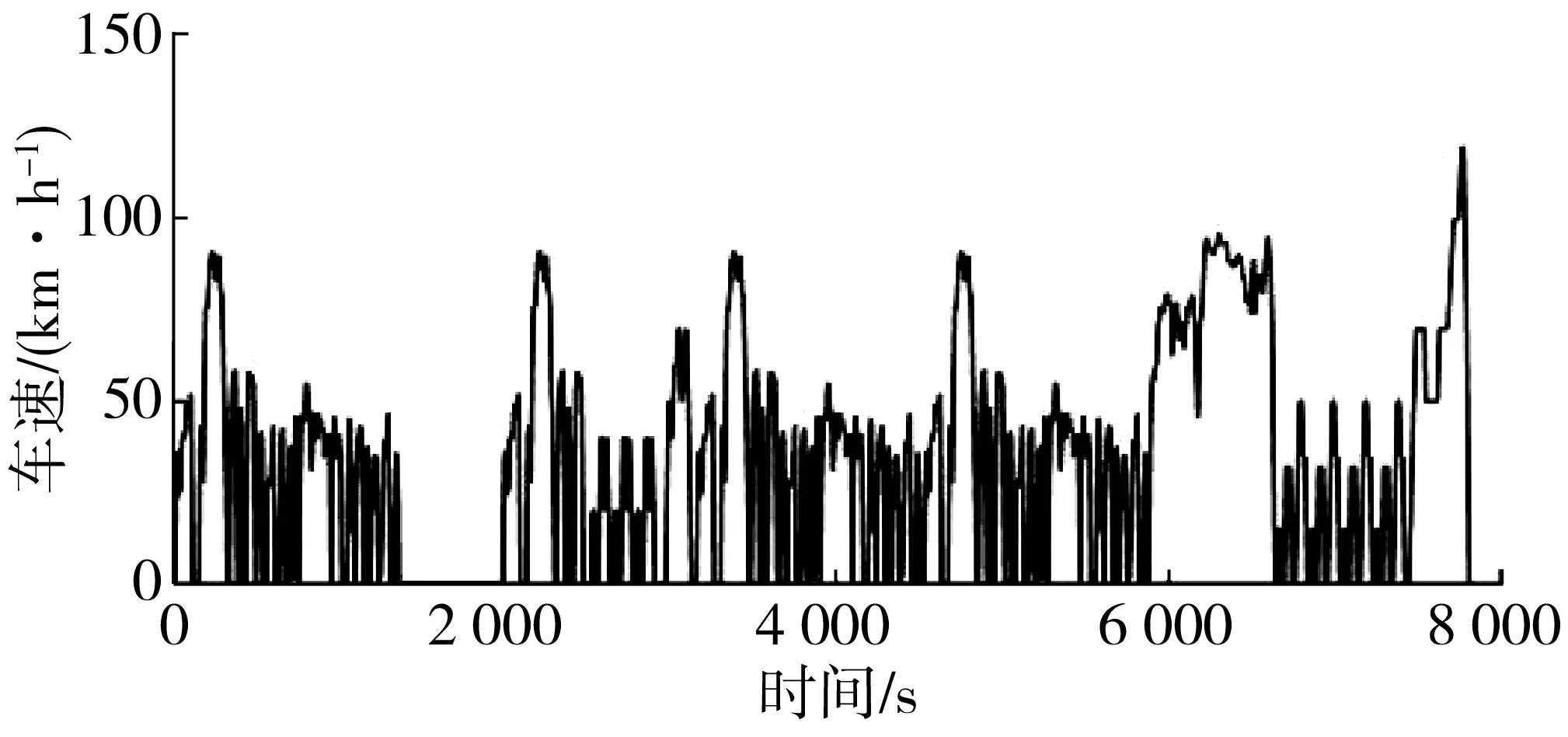
图11 组合工况Fig. 11 Combined working condition

图12为目标函数值迭代值，随着迭代次数增加，平均燃油经济性不断收敛至最佳状态，最终值为63.0 mile/gal，优化后的隶属度函数如图13。需求功率隶属子函数图13(a)在36 kW(增程器最优经济点)处范围最大，区别于其他功率区间；SOC隶属子函数图13(b)则集中于0.5～0.7(动力电池高效率区间)；增程器隶属子函数图13(c)跟优化前相比变化不大，也说明了基于DP提取的模糊控制规则对协调整车能量分配的正确性。

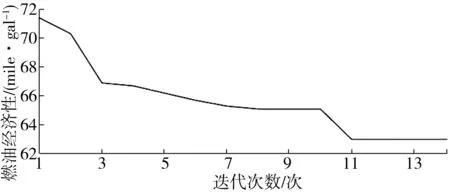
图12 目标函数迭代值Fig. 12 Iterative value of objective function

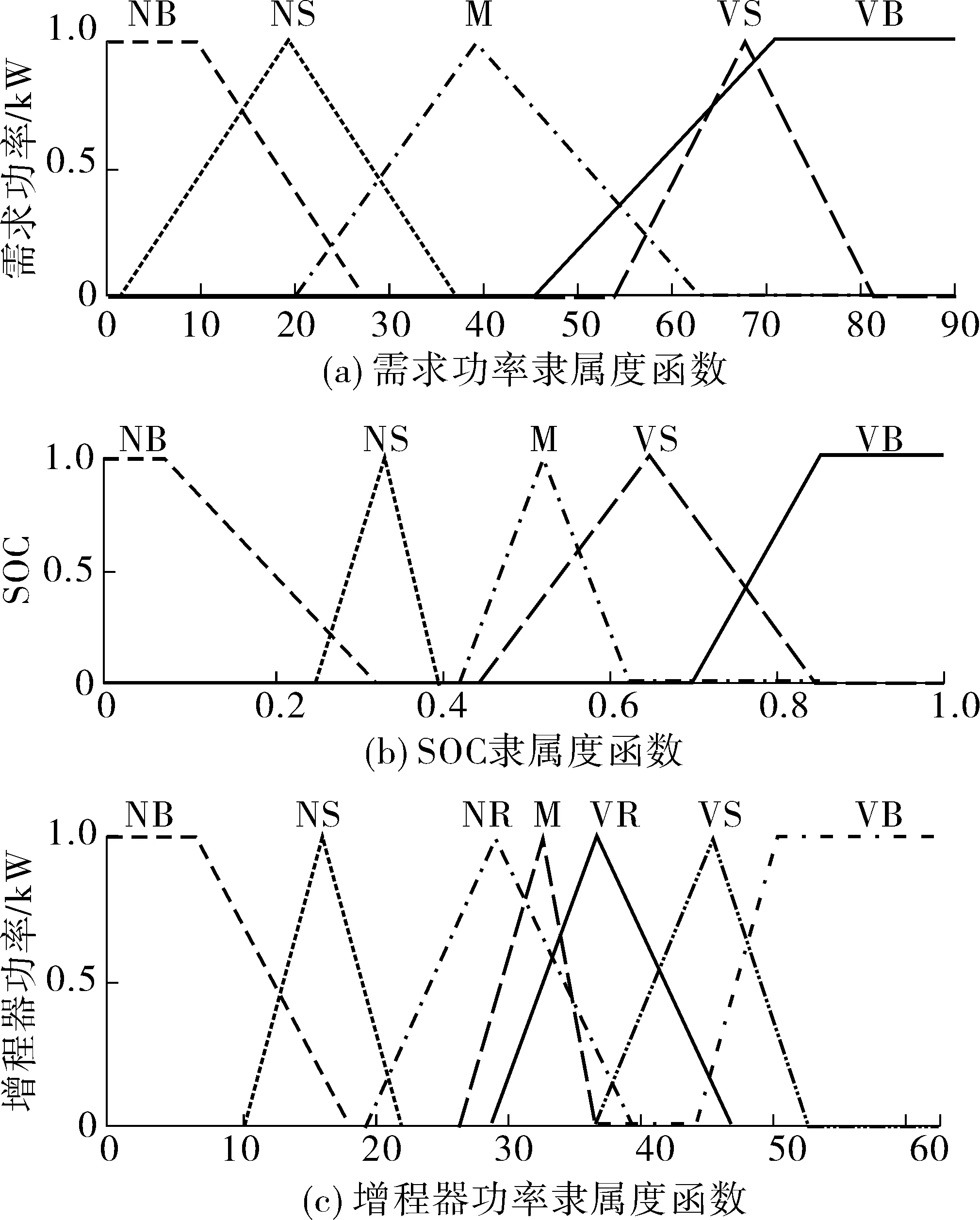
图13 优化后的隶属度子函数Fig. 13 The subfunction of membership degree after optimization

4.1 仿真结果分析

将优化后的部分控制策略及隶属度函数参数带入EREV全局优化控制策略模型，利用ADVISOR软件平台进行仿真。图14分别为动力电池SOC值变化曲线、增程器输出功率和动力电池输出功率。

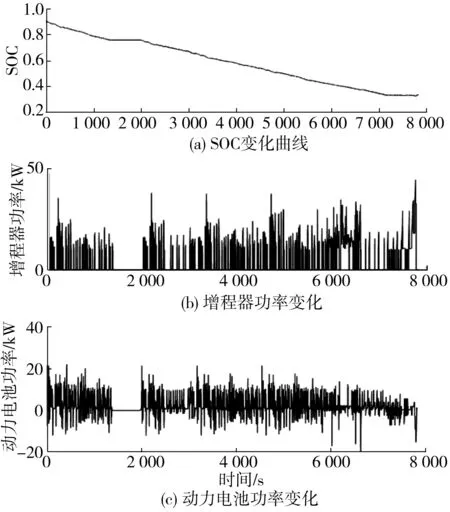
图14 组合工况仿真Fig. 14 Simulation of combined working condition

从图14可知，在整个组合工况运行下，动力电池SOC值下降较为缓慢，且输出功率基本在15 kW以内，最大输出功率不超过21 kW，有效防止高电流对动力电池寿命的影响；仿真快结束时，SOC值维持在相对稳定的状态下(0.33左右)，便于动力电池下一次充电；增程器可以沿着最优效率曲线输出功率，避免了因功率过高或过低造成整车控制系统效率下降。为了验证基于全局优化的EREV模糊控制策略适用于不同工况，将组合工况分为单独工况进行运行仿真，图15为5种分工况SOC变化曲线。

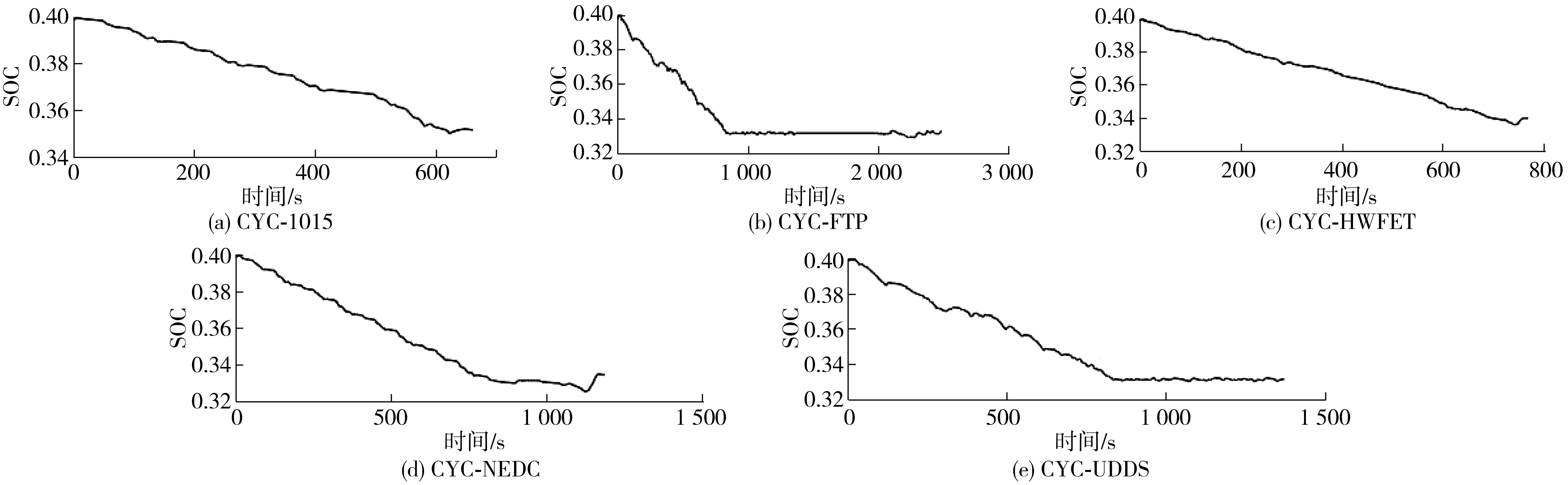
图15 分工况SOC分布Fig. 15 SOC distribution under different driving cycles

将优化后的控制策略参数及模糊隶属度参数应用到笔者所制定的全局优化控制策略中，并将其嵌入到ADVISOR整车模型中进行仿真。如图15，所提策略可以适用于多种工况，能够合理地分配动力电池与增程器间的功率，动力电池SOC值能维持在0.33附近。表3给出了不同工况下的总油耗对比，可见无论是组合工况还是分工况，其燃油消耗量对比功率跟随式控制策略均有所降低。综上所述，本策略能有效提高EREV燃油经济性，节能减排。

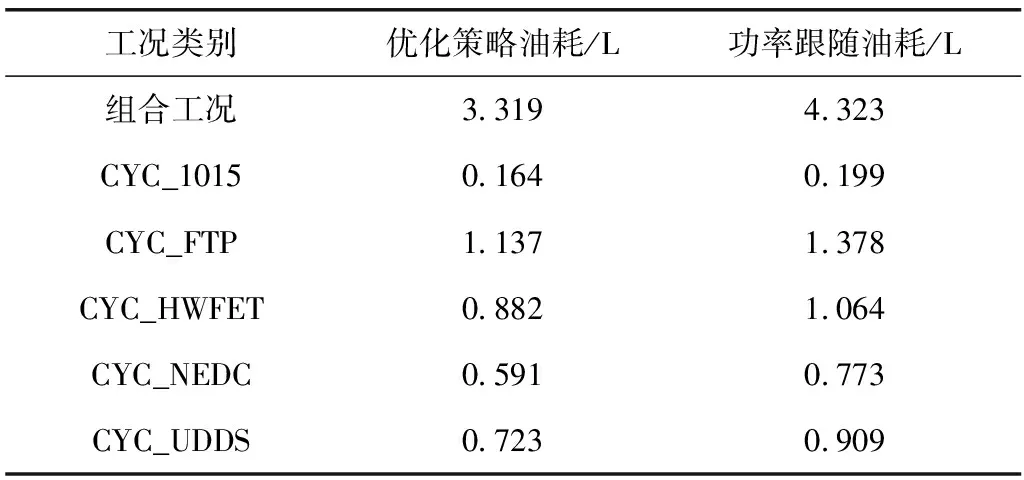
表3 工况油耗对比及优化后的控制策略参数Table 3 Comparison of fuel consumption under working conditions and optimized control strategy parameters

4.2 在环试验验证

为进一步验证所提策略的有效性，依托研发生产一体化(development to prodution，D2P)技术实现在环试验验证，对所提模糊控制策略进行实车验证。D2P具有快速开发整车控制策略功能，主要包括MotoHawk、GCC代码编辑器以及软件检测Mototune。通过在MATLAB/Simulink中建立的基于全局优化的模糊控制策略模型替换到MotoHawk模块中，并根据优化后的参数完成修改与调试；通过GCC对模型进行编译，以便主控制器进行识别；最后完成CAN总线的连接。为凸显本控制策略在维持SOC值稳定的同时，依然能根据实时仿真工况使增程器处在高效率区间工作，设置动力电池SOC初始值为0.33，并选用CYC_NEDC作为在环循环工况。图16为基于D2P技术在环实验平台。

图17为实测在环实验数据，由图17可见：SOC在整个NEDC循环工况中始终维持在相对稳定的状态，且最大峰值差值小于0.01，有助于延长动力电池使用寿命；增程器工作点大部分处在[0.30～0.35]区间范围内，工作点效率较高，有利于提高整车经济性。表4为两种能量管理策略的燃油经济性在环试验对比数据，由表4可知：采用优化控制策略比未采用优化控制策略的燃油消耗较少0.166 L，燃油经济性提高21.3%；与表3相比，两种能量管理策略的在环试验结果均比整车仿真结果燃油经济性有所降低，可能是在环实验中外在因素导致燃油消耗增加。

图16 基于D2P技术在环实验平台Fig. 16 In loop experimental platform based on D2P technology

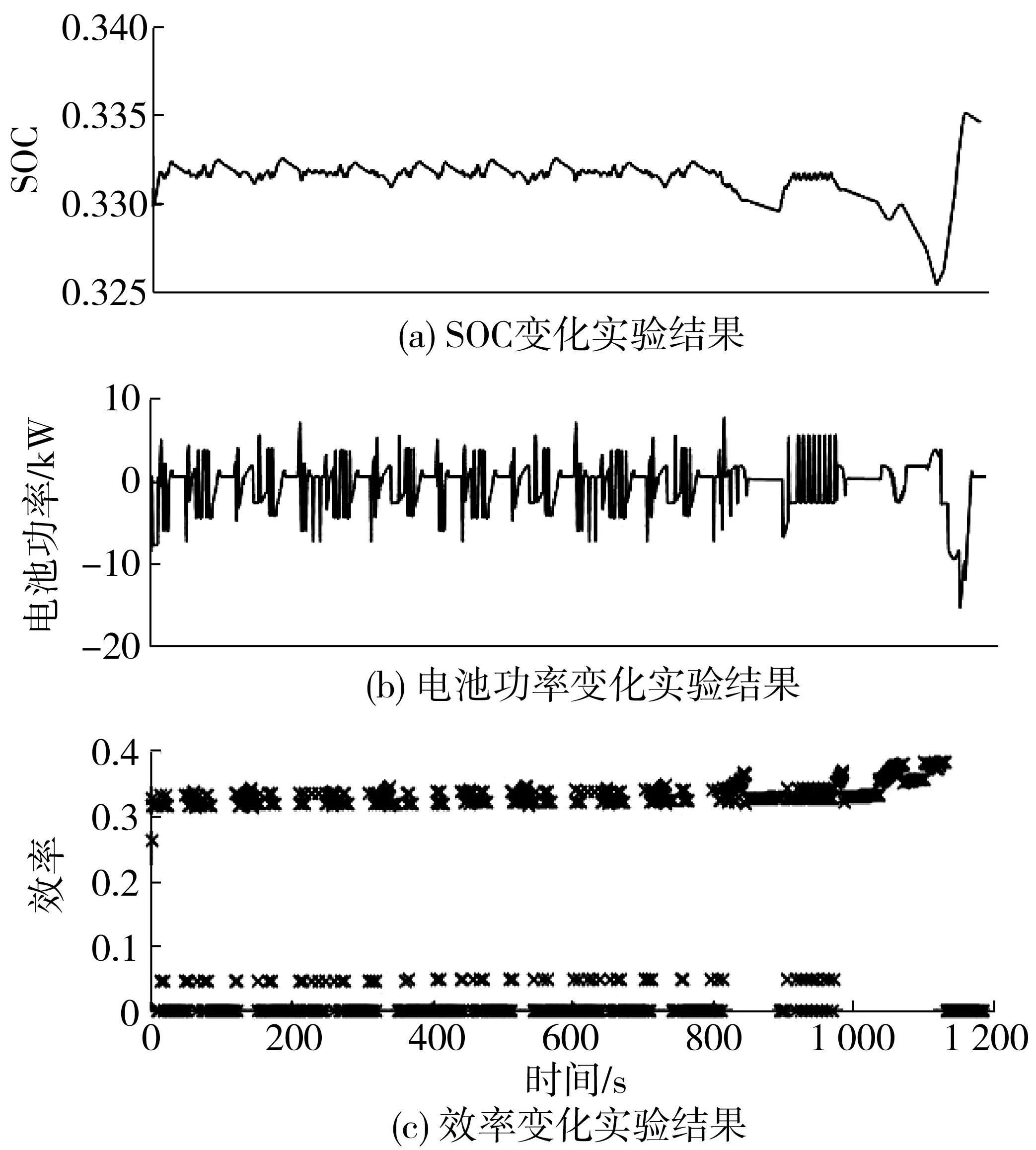
图17 实测实验数据Fig. 17 Measured experimental data

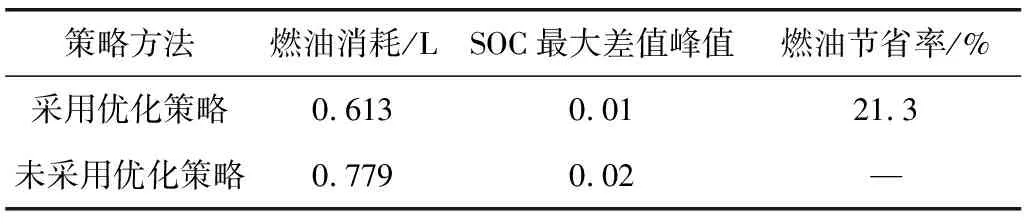
表4 燃油经济性对比Table 4 Fuel economy comparison

5 结 论

以增程式电动汽车为研究对象，提出一种基于全局优化算法的EREV模糊控制系统能量管理策略。

1)以EREV最优效率曲线做为增程器工作区间，在不同动力电池及工况状态下，得出动态规划算法对能量分配的规则，以及仿真结束后动力电池所维持的状态；根据DP规则以及工程经验建立EREV模糊控制规则，并利用粒子群算法对控制策略及模糊隶属度函数进行优化，从而建立了全局优化的EREV能量管理策略，并进行了仿真验证。

2)仿真结果显示，循环工况结束后动力电池维持在相对稳定的状态点下，与Advisor中原功率跟随式控制策略相比，整车燃油消耗及排放均有所改善，且发动机长期工作在高效经济区间。

3)基于D2P技术对本控制策略进行在环试验验证，将建立的控制策略模型替换到MotoHawk模块中，实现软硬件结合，在环实验结果显示，采用优化管理策略对比与未采用优化管理策略的整车燃油经济性有明显提高，但略低于整车模型仿真。