多因素影响下水工隧洞最小覆盖层厚度力学分析
杨自友,程长清,孙天宇,俞 凡,杨 明
(安徽建筑大学 土木工程学院,安徽 合肥 230601)
0 引 言
目前,水工隧洞最小覆盖层厚度的计算准则主要有水力劈裂准则、初始应力场最小主应力准则、雪山准则、挪威准则等,但这些计算准则均不适用于深埋水工隧洞的计算。由岩体的弹塑性理论可知,当水工隧洞内水压力过大时,内部岩体会出现塑性变形,水工隧洞最小覆盖层厚度可由塑性区半径转换得到,但该理论未考虑外水[1]、衬砌等因素对最小覆盖层厚度的影响;荣传新等[2]假设衬砌内壁处渗透水压力为0,基于流固耦合理论进行煤矿立井弹塑性力学分析,但实际上,透水的混凝土衬砌材料的内壁处渗透水压力往往不为0,该模型未考虑内水压力对塑性区的影响,同时未考虑岩体与衬砌渗透系数对塑性区分布的影响;张常光[3]提出了基于统一强度理论计算施工期和运行期水工隧洞应力和位移的方法,但在计算塑性区弹性应变时,该方法考虑弹性应变为常量且未进行最小覆盖层厚度计算;王睢等[4]、李宗利等[5]分别采用D-P准则、M-C准则计算了水工隧洞的弹塑性解,但计算中未考虑衬砌、岩土体剪胀性等因素对塑性区的影响;S. K. SHARAN[6]、蔡海兵等[7]、C. CARRANZ-TORRES等[8]提出了基于广义Hoek-Brown准则的岩土体位移计算模型,分析了考虑岩土体剪胀与否的塑性区位移变化规律,但该模型也不能反映水工隧洞在不同内水压力下引起的围岩塑性区变化;范浩等[9]、张常光等[10]利用统一强度理论分析了渗流情况下隧洞的稳定性;漆江等[11]将外水压力视为体积力分析了围岩的稳定性;赵均海等[12]、潘继良等[13]分别基于渗流和不同强度理论分析了围岩的稳定性。
笔者分别采用Drucker-Prager(D-P)准则和统一强度理论,考虑渗流[14-15]、剪胀性[16-17]、衬砌等因素,并将塑性区弹性应变视为变量,计算了水工隧洞最小覆盖层厚度h,分析了渗透系数k、中间主应力[18]系数n、强度参数c、φ等对于最小覆盖层厚度h[19]的影响。
1 统一强度理论与D-P准则
1.1 统一强度理论
统一强度理论同时考虑了单元体上所受到的正应力与剪应力对材料破坏的贡献,其数学表达式如式(1)、式(2):
(1)
(2)
式中:b为反映中间主剪应力及相应面上正应力对材料屈服或破坏影响程度的系数;c为材料的黏聚力,MPa;φ为材料的内摩擦角,(°);σ1、σ2、σ3分别为最大、中间、最小主应力,MPa。
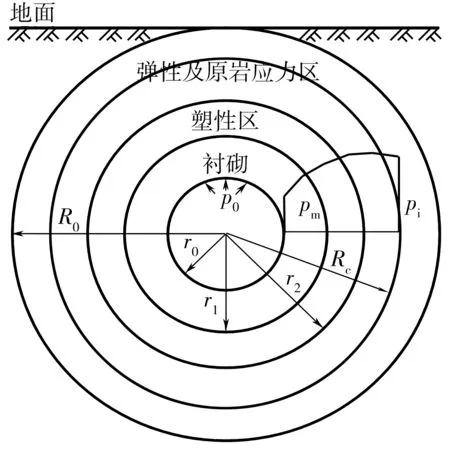
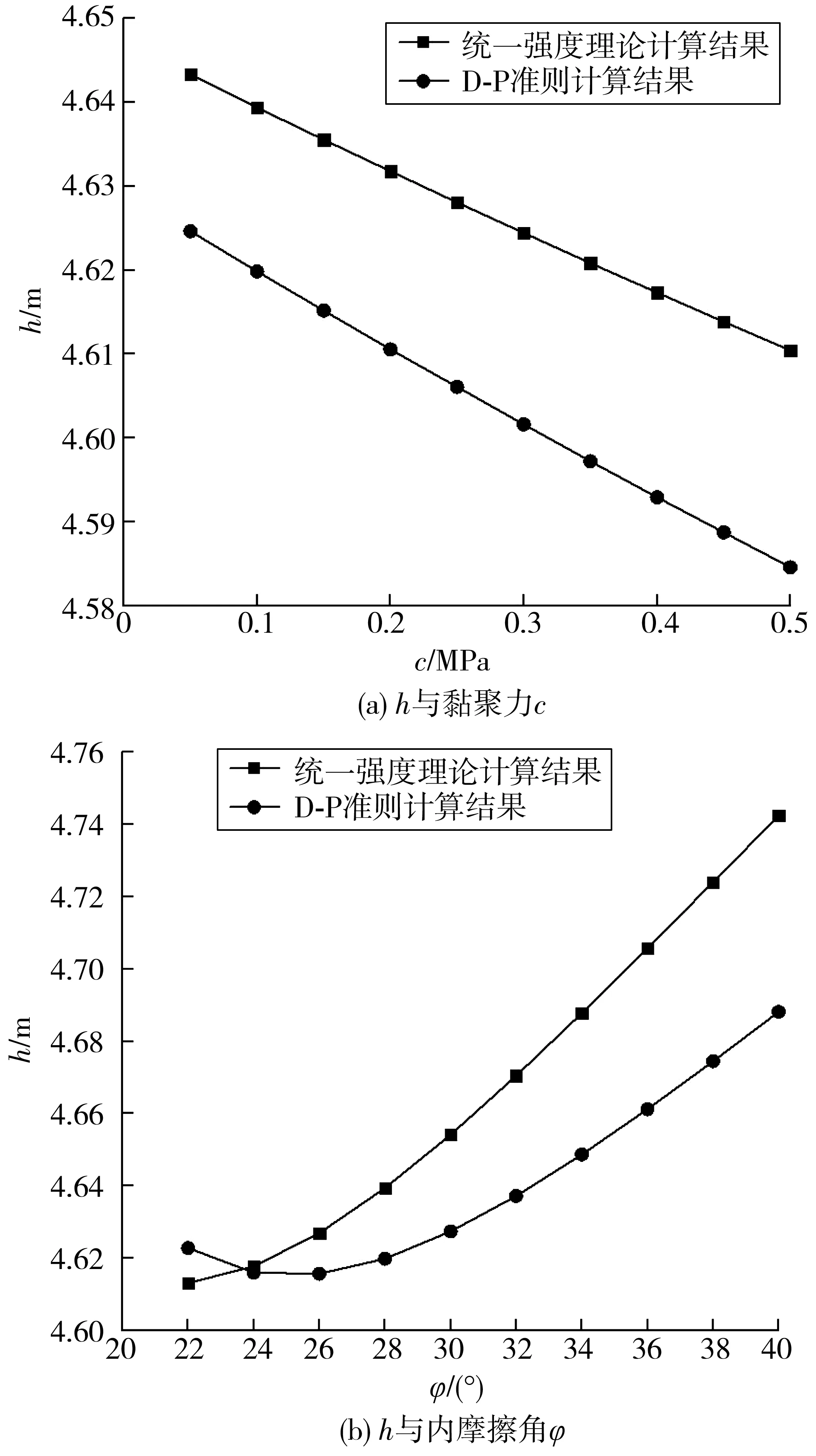
当b=0时,统一强度理论可退化为Mohr-Coulomb准则;当b=1时,可退化为双剪强度准则;当0 对于塑性岩体中的平面应变问题,由文献[3]可知: (3) 于是,统一强度理论数学表达式可转化为 (4) 笔者提出水工隧洞最小覆盖层厚度的要求,主要是为了防止内水压力过大导致上部岩体被掀起。水工隧洞在输水运行过程中,大主应力为环向应力σθ,小主应力为径向应力σr[5],因此分析过程中取σ1=σθ,σ2=σr,有 σθ-Aσr=B (5) 式中:A=[2(1+sinφ)(1+b)-b(1-sinφ)]/[(b+2)(1- sinφ)];B=[4ccosφ(1+b)]/[(1-sinφ)(b+2)]。 D-P准则同时考虑应力偏张量第二不变量与应力张量第一不变量,建立符合岩土体的圆锥形屈服曲面,其数学表达式如(6)、式(7): (6) (7) 引入反映σ1、σ2、σ3之间关系的中间主应力系数n〔n=(σ2-σ3)/(σ1-σ2)〕,由σ1≥σ2≥σ3可知:0≤n≤1,于是 σ2=nσ1+(1-n)σ3 (8) 将式(8)代入式(7),得 I1=(1+n)σ1+(2-n)σ3 于是,D-P准则可简写为 σθ-Cσr=D (9) ①隧洞为连续、均匀、各向同性的理想弹塑性体; ②隧洞为圆形,无限长; ③忽略隧洞影响范围内的岩体自重; ④原岩应力为各向等压状态; ⑤衬砌为理想弹性材料。 简化后有压水工隧洞弹塑性区分布模型如图1。 r0、r1分别为衬砌的内、外半径,m;r2为塑性区半径,m;Rc为当隧洞围岩稳定渗流的外水压力与原始渗流外水压力相同时的半径,m;R0为水工隧洞中心到地面的距离,m;p0为衬砌内水压力,MPa;pm为r0处的渗流外水压力,MPa;pi为原始渗流外水压力,MPa。 图1 有压水工隧洞弹塑区分布Fig. 1 Elastic-plastic zone distribution of pressurized hydraulic tunnel 根据地下水连续方程及达西定律,渗流微分方程如式(10): (10) pw按式(11)或式(12)计算[1]: (11) (12) 式中:pw为渗流体积力,MPa;kc、kd分别为混凝土衬砌与围岩的渗透系数, cm/s;其他符号同前。 力的平衡方程为[2] (13) 而考虑渗流的统一强度理论为 (σθ+ηpw)-A(σr+ηpw)=B (14) 将式(14)、式(12)代入式(13),得到 (15) 求解式(15)得: (16) 考虑边界条件 (17) 求得 (18) 从而,得到塑性区应力分布解析解表达式 (19) (20) (21) (22) 当r=r2时,弹性区应力同样满足式(14),考虑弹塑性界面上的应力连续,有 (23) (24) 考虑围岩的剪胀性,同时考虑塑性区弹性应变为变量,则塑性区位移为[7] (25) 工程实际中,二次混凝土衬砌不允许出现塑性破坏,故按照完全弹性体对衬砌进行计算。 几何方程: (26) 本构方程: (27) 将式(26)代入式(27),再联合式(11),一并代入式(13),得 (28) 对式(28)进行积分,得 (29) 将式(29)代入式(26),再代入式(27),得 (30) 考虑边界条件 (31) 求解得到C2、C3: (32) (33) 将式(32)、式(33)代入式(29)中,令r=r1,β=(1 + sinψ)/(1-sinψ),联立式(29),可求得p1;再根据式(24),可求得塑性区半径r2。 最小覆盖层厚度h按式(34)计算[19]: h=ωr2-r1 (34) (35) (36) (37) (38) 根据文献[3],某水工隧洞半径r1=2.5 m。围岩力学参数Ed=20 000 MPa,μd=0.3,c=0.1 MPa,φ=28°,地应力q=1.0 MPa,剪胀系数β=1,围岩渗透系数kd=5.0×10-4cm/s。混凝土衬砌内半径r0=2 m,外半径为r1=2.5 m,衬砌相关参数为Ec=30 000 MPa,μc=0.15,混凝土衬砌渗透系数kc=1.0 × 10-7cm/s。衬砌承受内水压力p0=6 MPa。其他相关参数pi=1.0 MPa,pm=0.5 MPa,η=1.0,由钻孔实验及抽水试验知Rc=8r1。 据分析,由统一强度理论求解的最小覆盖层厚度h受β,kd/kc,b,c,φ等因素影响;由D-P准则计算的最小覆盖层厚度h受β,kd/kc,n,c,φ等因素影响。 当c=0.1 MPa,φ=28°,混凝土渗透系数kc不变,中间主应力系数n=0.5时,剪胀系数β对最小覆盖层厚度h的影响曲线如图2。 图2 β-h的关系曲线Fig. 2 Relationship curves of β-h 由图2可以看出: 1)随着β的增大,无论是采用D-P准则还是统一强度理论,计算得到的h值均逐渐增大。 2)当β=2.0~2.2,两条曲线相交,说明此时两者h值一致,在此点,剪胀系数对两种理论计算结果的影响是一致的。 3)当β=1.0→2.77,采用D-P准则,计算的h值从2.92 m变化到5.27 m,相差2.35 m,增大了约80.5%;采用统一强度理论,计算的h值从3.08 m变化到5.20 m,相差2.12 m,增大了约68.8%。两种理论计算结果均表明:剪胀系数β对最小覆盖层厚度计算结果影响较大,且在剪胀系数增大相同时,采用D-P准则计算的结果增大更快。 当c=0.1 MPa,φ=28°,β=2.0,n=0.5时,围岩与混凝土衬砌渗透系数比kd/kc对最小覆盖层厚度h的影响曲线如图3。 图3 kd/kc-h的关系曲线Fig. 3 Curves of kd/kc-h 由图3可以看出: 1)在kd/kc=0→5阶段,采用两种理论计算的h值均急速减小。采用D-P准则计算的h值从5.22 m变化到3.70 m,相差1.52 m,减小了29.2%;采用统一强度理论计算的h值从5.02 m变化到3.93 m,相差1.09 m,减小了21.7%。此阶段,kd/kc越大,h值越小。 2)在kd/kc=5→500阶段,h值逐渐增大。 3)在kd/kc=500→5 000阶段,随着kd/kc的增大,h值几乎无太大变化,两种理论计算结果约为4.60 m。 4) 当不考虑渗流时(η=0),采用D-P准则与采用统一强度理论计算的最小覆盖层厚度分别为8.92、8.42 m,比kd/kc=500→5 000阶段即考虑渗流场情况下的最小覆盖层厚度分别增大了93.91%、83.04%。可见不考虑渗流场时,岩体有效应力增大,相当于增大了最小覆盖层厚度。因此在计算中不能忽略外水对最小覆盖层厚度影响。 当渗透系数比kd/kc不变,中间主应力系数n=0.5,剪胀系数β=2,其他参数不变时,岩石强度参数与最小覆盖层厚度h的关系曲线如图4。 图4 h-c、h-φ的关系曲线Fig. 4 Relationship curves of h-c, h-φ 由图4可以看出: 1) 随着c的增大,两种理论计算的h值均呈现线性减小趋势。 2) 当φ=22° → 40°时,采用统一强度理论计算,h=4.61 m→ 4.74 m,增长率为2.82%;采用D-P准则计算,h值先减小后增大,曲线呈现下凹的特点,当φ=26°时,h值达到最小。 综上,在设计中,应选取c值较大而φ≈26°的岩层,这样能够有效地减小最小覆盖层厚度。 当c=0.1 MPa,φ=28°,渗透系数比kd/kc不变,剪胀系数β=2时,中间主应力系数n与最小覆盖层厚度h的关系曲线如图5。由图5可以看出: 1)随着中间主应力系数n的增大,统一强度理论计算的h值逐渐增大。 2)D-P准则计算的h值先减小后增大,表明D-P准则计算结果更符合实际情况。曲线在中间主应力系数n=0.3、0.7附近出现拐点,体现了中间主应力的区间性。 图5 h-n的关系曲线Fig. 5 Relationship curves of h-n 1) 分别推导了采用统一强度理论和D-P准则,考虑渗流、衬砌模型的最小覆盖层厚度计算公式。由统一强度理论求得的理论解可以衍生出许多其他解:当b=0时,统一强度理论可退化为M-C准则计算结果;当b=1时,可退化为双剪强度准则计算结果;当b=0~1时,可得到一系列新解答;当η=0时,可得到不考虑渗流的计算结果;当β=1.0时,可得到不考虑岩体剪胀性的解答。 2) 随着岩体内摩擦角φ的增大,采用统一强度理论计算的h值逐渐增大,采用D-P准则计算的h值先减小后增大;随着黏聚力c的增大,无论采用D-P准则还是统一强度理论计算,h值均逐渐减小。因此,设计中应尽量取c较大而φ≈ 26°的岩体。 3) 随着剪胀系数β的增大,两种理论计算的h值均逐渐增大;当β=2.0~2.5时,两种理论计算的h值较为接近;随着中间主应力系数n的增大,采用统一强度理论计算的h值增大,而采用D-P准则计算的h值出现波动,体现了中间主应力的区间效应。 4) 当岩体与衬砌渗透系数的比kd/kc相差较大时,最小覆盖层厚度无太大变化;当不考虑渗流时,最小覆盖层厚度较考虑渗流时出现较大的波动。因此,设计中宜控制kd/kc≈500。
1.2 D-P准则
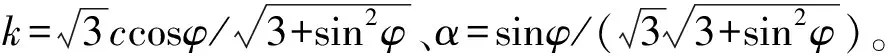
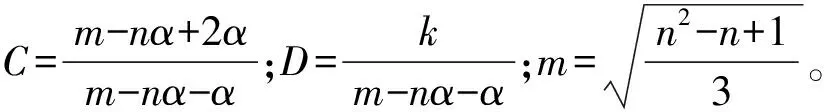
2 基于统一强度理论的有压隧洞最小覆盖层厚度计算
2.1 基本假定
2.2 渗流场分析
2.3 围岩应力分析
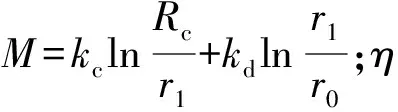


2.4 围岩塑性区位移分析
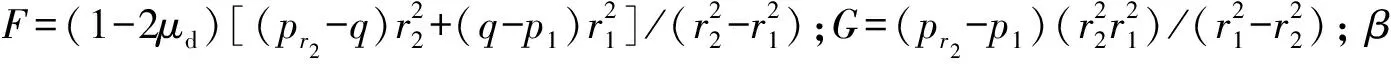
2.5 混凝土衬砌应力分析

3 基于D-P准则的有压隧洞最小覆盖层厚度计算
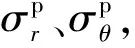
4 案例分析
4.1 剪胀系数对最小覆盖层厚度影响

4.2 渗透系数比对最小覆盖层厚度影响

4.3 强度参数对最小覆盖层厚度影响
4.4 中间主应力系数对最小覆盖层厚度影响

5 结 论

