超材料混凝土单胞骨料的有阻尼自由振动特性研究
韩 洁, 路国运, 赵一涛
(1. 太原理工大学 土木工程学院,太原 030024; 2. 太原市政工程勘测设计院有限公司,太原 030002)
超材料的提出最早可追溯到1999年[1],这种复合材料具有非常规性能,如负折射率、负磁导率或负有效质量等性质[2-7]。超材料混凝土是将传统混凝土中的粗骨料用复合材料所制的球形骨料取代[8]。随着科学技术迅猛发展,超材料混凝土结构抵抗爆炸高压动态载荷、消能减震、冲击抗振和保护成为工程界研究的热点之一,激发了广大学者的极大兴趣。其主要应用在振动设备基础、高速铁路平板轨道、核电站、海洋平台、防空洞等大型工程领域。
杜秋姣等[9]设计发明了一种地震超材料,其单胞由特定物理参数的橡胶块和钢块构成,钢块封闭在橡胶块中,能大幅度衰减带隙范围内的地震波,通过调节地震超材料单胞的几何参数可以获得不同频段处的带隙,从而适应固有频率不同的建筑物。Finocchio等[10]设计了一种地震超材料(seismic metamaterial,SM),发现:当SM建在地面上时,土壤的放大功能会显着地降低,能减弱S波对放置在上方的建筑物的影响的影响;SM的内部共振频率与建筑物的基本共振频率一致。Yan等[11]研究了由周期性材料制成的周期性基础,发现:这种基础提供的低频带间隙,涵盖了地震波的主要频率范围,能够在地震中有效的保护上部结构;当晶胞尺寸为0.305 m时,绝对理论带隙的起始频率最低可达到32.9 Hz。测试数据表明:当输入波落入衰减区时,与没有周期性基础的相同结构相比,上部结构的响应会降低90%以上;不同频率的输入波,在3D周期性基础的顶部衰减的百分比是接近的。输入地面的水平运动对衰减区域的影响可忽略不计。郜英杰等[12]设计了一种超材料消波混凝土(super-material wave absorbing concrete,SMWAC)板,数值模拟结果表明:与普通混凝土板相比,SMWAC板有更好的消波能力,在振动波传播过程中,应力也得到大幅度衰减;通过改变SMWAC板聚合体的隔层材料,使SMWAC板能够消减不同频率段机械波;SMWAC板中各材料比例不变时,聚合体尺寸较大时,消波效果更明显。
综上所述,已有对骨料动力行为的研究主要集中在试验与数值模拟,其理论研究还不够深入、尤其是骨料的振动问题研究。基于此,本文以骨料胞元为研究对象,建立其三维振动模型,由达朗贝尔原理导出了有阻尼自由振动的控制方程,设振动方程的复数解,得到固有频率。利用初始条件,获得有阻尼振动解。用MATLAB软件编程进行算例分析,讨论了初始条件、骨料尺寸、软涂层和砂浆的弹性模量等参数对固有频率和振动特性的影响。
1 方程建立
1.1 模型建立
基于Mitchell研究中的一维模型,考虑了砂浆和软涂层三维效应及阻尼,建立了超材料混凝土单胞骨料的三维振动模型,弹簧总刚度为k[13],c为等效阻尼,如图1所示。图2是骨料模型。
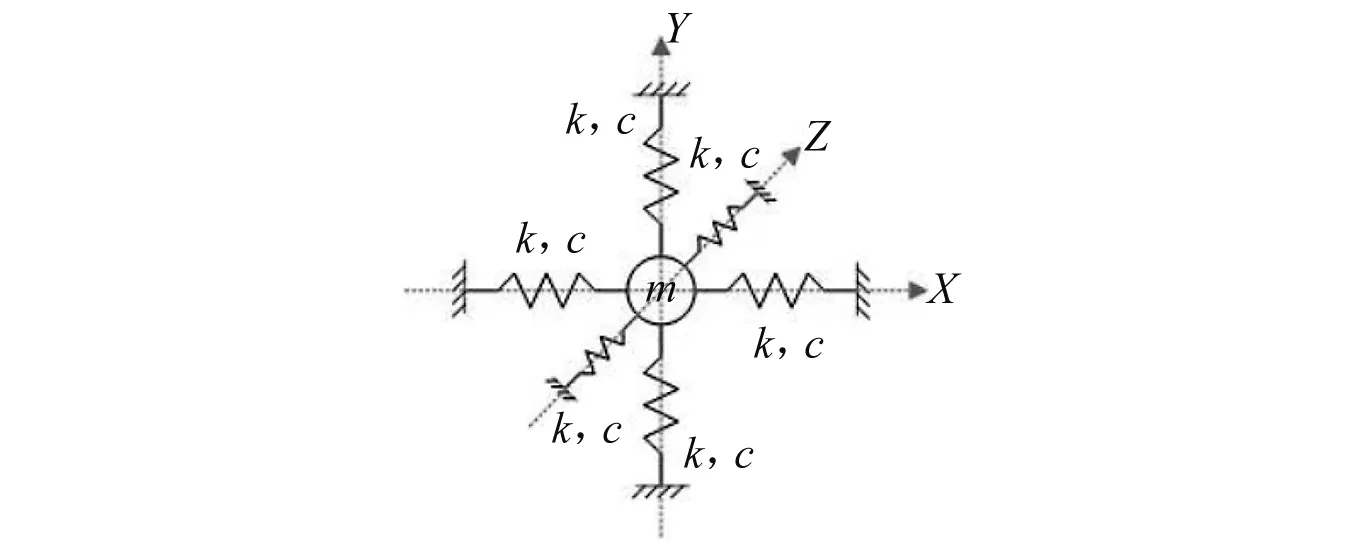
图1 三维振动模型示意图Fig.1 Three-dimensional vibration model

图2 骨料模型图Fig.2 The unit cell aggregate model
模型中,骨料由重核(高密度重金属球芯)与软涂层(涂在球芯外表面的轻薄柔软外层)组成,骨料位于边长d为0.03 m的立方体砂浆块中心,重核质量为m,半径为r,软涂层厚度为ts,软涂层和砂浆由弹性弹簧等效代替,其等效刚度分别为ks和km,ks和km串联总刚度为k,砂浆的等效长度为lm,弹簧总长度为l=ts+lm。yd为模型的竖向位移;Δl为弹簧的伸长量;Em,Es分别为砂浆和软涂层的弹性模量;lm,ks,km计算如下
(1)
1.2 方程推导
模型变形示意图如图3所示,在线弹性振动时,受力图如图4所示(XOZ,ZOY的变形、受力图与XOY的一致)。

图3 模型变形示意图Fig.3 Model deformation diagram

图4 重核受力图Fig.4 Force diagram
其几何关系为
yd=lθ,Δl=ydθ
(2)
c1,c2为砂浆和软涂层的黏性阻尼系数,c为等效阻尼,三者关系为[14-16]
(3)
式中,ω,A分别为单胞骨料无阻尼自由振动的固有频率和振幅。
结合式(2)整理式(3)得到
(4)
则等效阻尼c和等效阻尼比ζ为
(5)
根据达朗贝尔原理得
(6)
结合式(2)整理得
(7)
式(7)是单胞骨料有阻尼的振动方程。
1.3 固有频率计算
设式(7)的复数解为
(8)
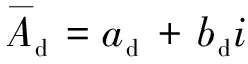
将式(8)代入式(7)整理得
0-2mζωωd+6cωd+
(9)
对式(9)求导、整理得
(10)
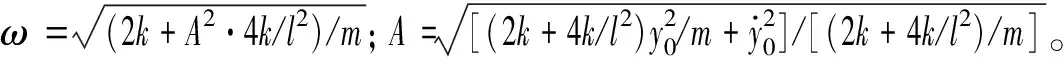
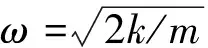
1.4 初始条件的影响
设初始位移、初始速度为
(11)
代入式(7)整理得
式(12)虚部为振动解,即
(13)
式(13)求导后代入式(11),化简得
(14)
整理式(14)得,振动解为
yd=Ade-ζωtsin(ωdt+αd)
(15)
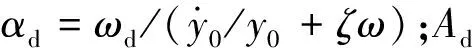
2 算例分析
用MATLAB编程进行算例分析,所取参数见表1[19-20]。表2是不同型号的骨料。
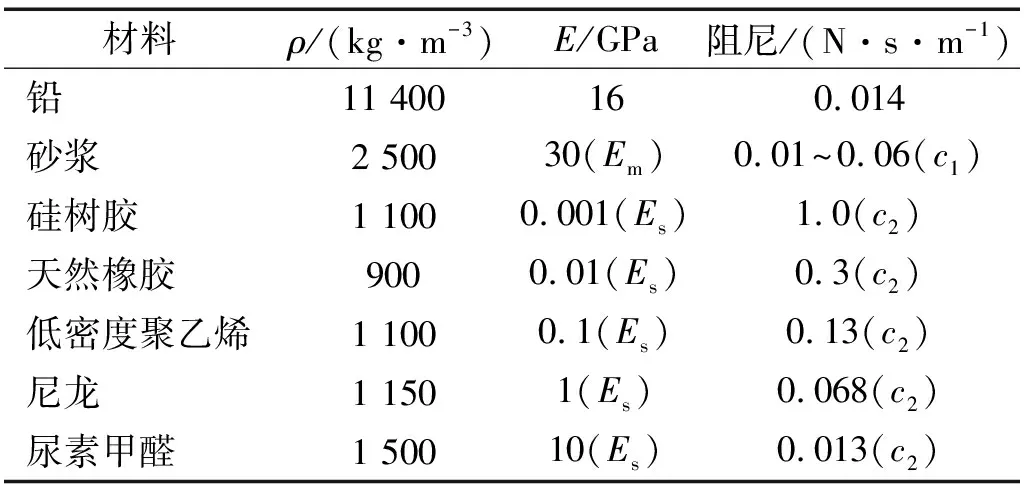
表1 骨料其他特征参数Tab.1 Aggregate parameters

表2 骨料型号Tab.2 Aggregate geometry data mm
2.1 参数对固有频率的影响


表3 有阻尼自由振动的固有频率Tab.3 Natural frequency with damped free vibration
结合式(1)、式(10)、表3可知:骨料外径相同时ωd C3<ωd B2<ωd A1;骨料型号相同时,固有频率随着软涂层弹性模量的增大而增大,即ωd 硅树胶<ωd 天然橡胶<ωd 低密度聚乙烯<ωd 尼龙<ωd 尿素甲醛;软涂层为同一种材料、骨料重核大小相同时,固有频率随着软涂层厚度的增大而减小,软涂层对频率有衰减作用,即ωd C3<ωd D4<ωd E5;与韩洁等和Mitchell所得结论一致。

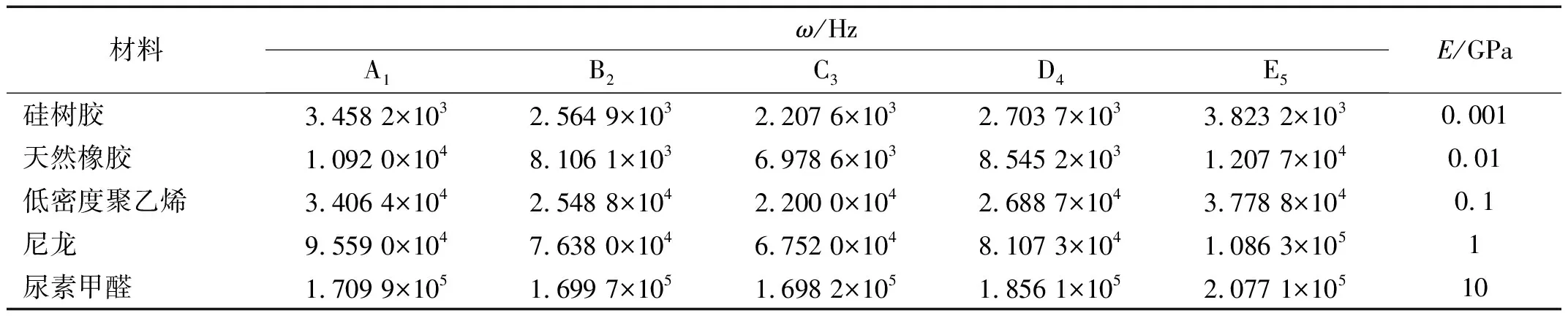
表4 无阻尼自由振动的固有频率Tab.4 Natural frequency with free vibration
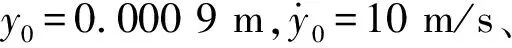

表5 不同软涂层材料下系统的等效阻尼比Tab.5 The equivalent damping ratio of the system under different soft coating materials
表5可知:骨料外径相同时,ζA1<ζB2<ζC3;骨料型号相同时,等效阻尼比随着软涂层弹性模量增大而减小,即ζ10 GPa<ζ1 GPa<ζ0.1 GPa<ζ0.01 GPa<ζ0.001 GPa;软涂层为同一种材料、骨料重核大小相同时,等效阻尼比随着软涂层厚度的增大而增大,即ζE5<ζD4<ζC3。
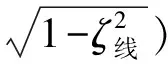
2.2 初始条件对振动的影响
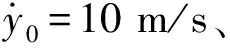

表6 不同初始位移下系统的振幅Tab.6 The amplitude of the system under different initial displacements
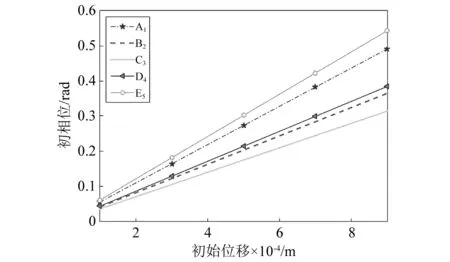
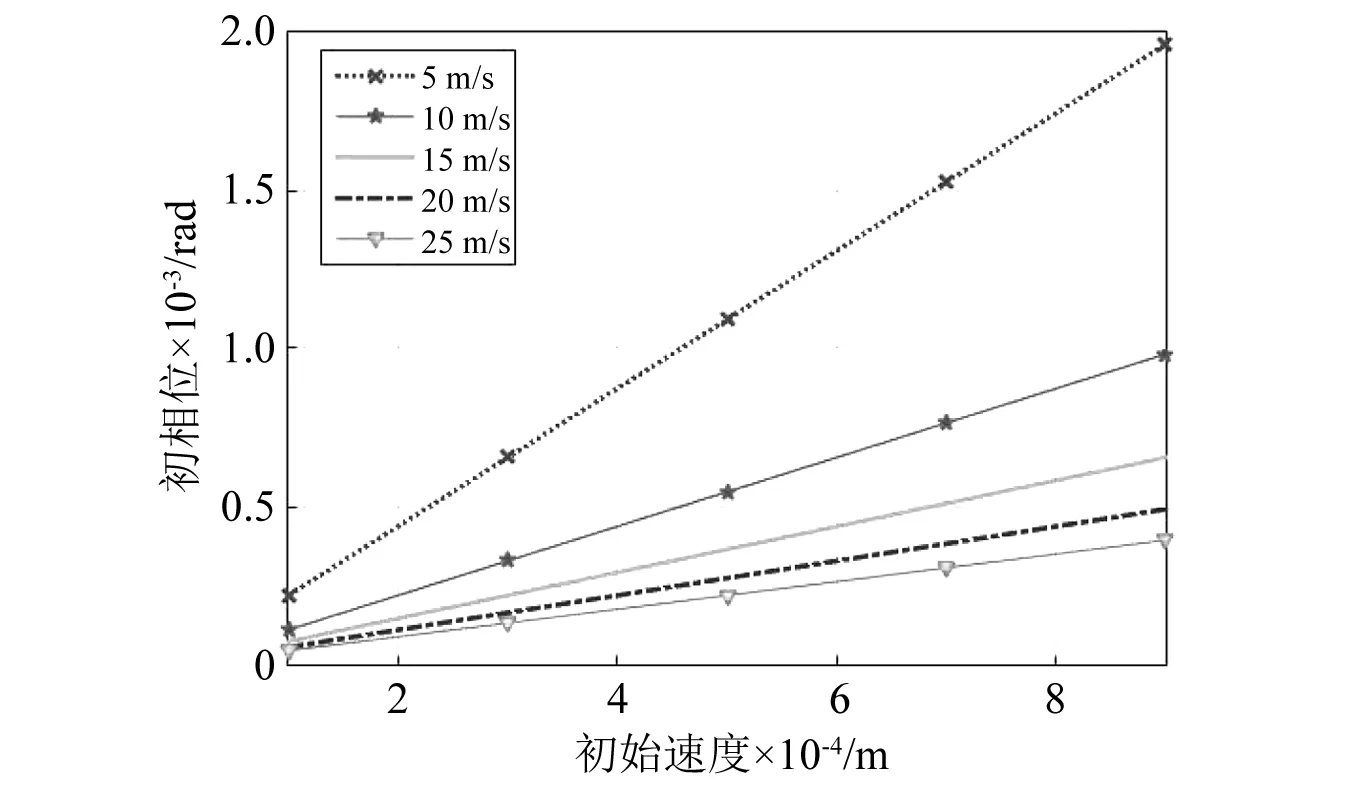
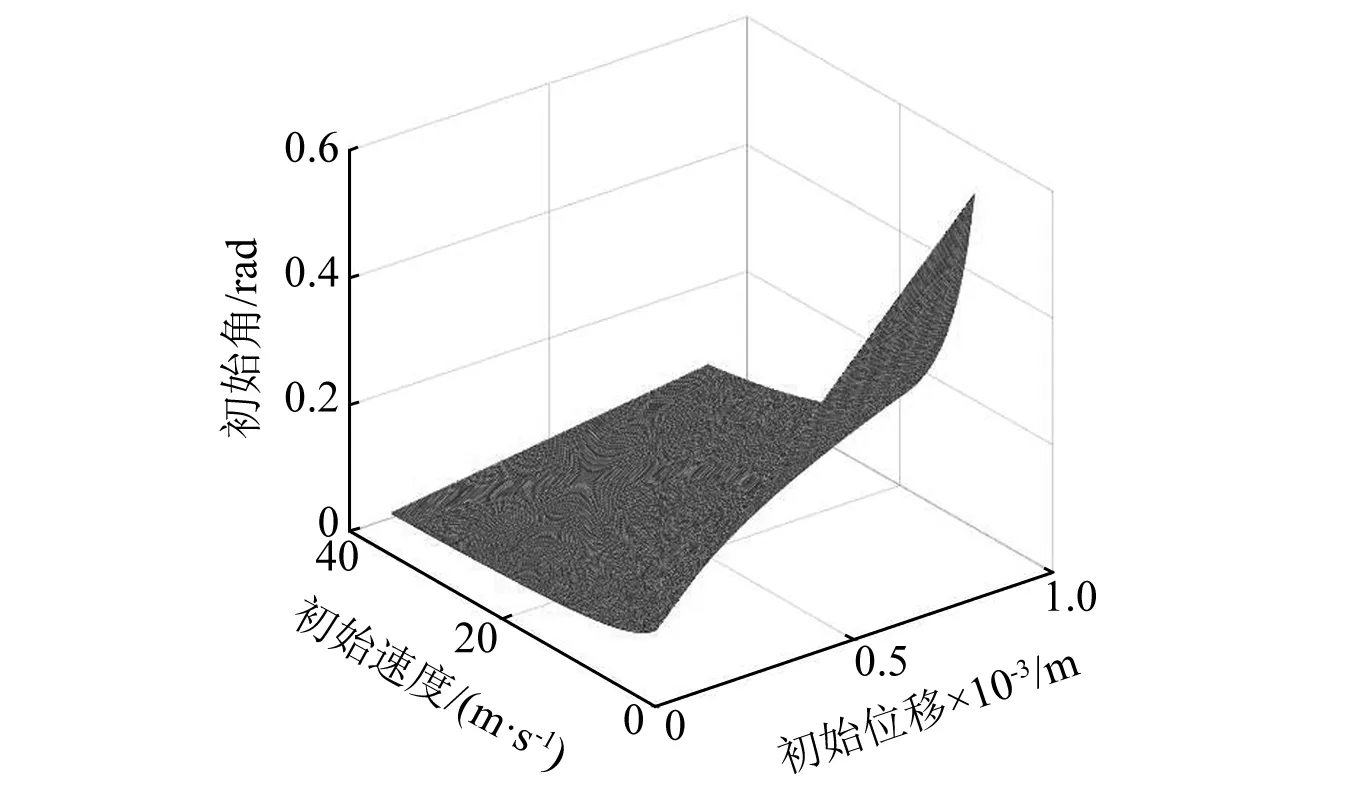
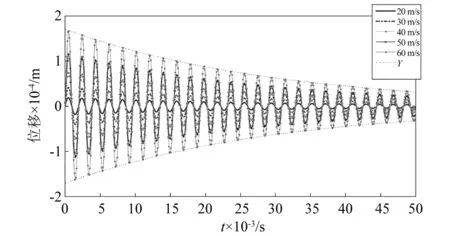
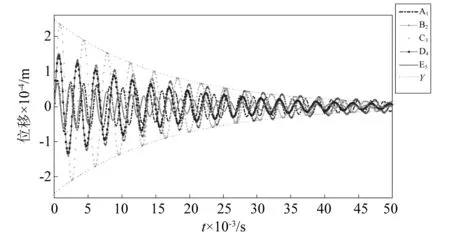
表6可知:骨料型号相同时,振幅随着初始位移的增大而增大,即Ad 0.000 1 m 表7是y0=0.000 9 m、尼龙材料作为软涂层材料、砂浆的阻尼系数中取0.06,初始速度分别为10 m/s,15 m/s,20 m/s,25 m/s,30 m/s,五种骨料下系统的振幅。 表7 不同初始速度下系统的振幅Tab.7 The amplitude of the system at different initial speeds 表7可知:骨料外径相同时,即Ad A1 表8 不同软涂层材料下系统的振幅Tab.8 The amplitude of the system under different soft coating materials 表8可知:骨料外径相同时,Ad A1 图5 初相位与初始位移的变化关系Fig.5 Relationship between initial phase and initial displaceme 图6是当选择A1组骨料、Es=0.01 GPa、砂浆的阻尼系数中取0.02时,初始位移分别为0.1 mm,0.3 mm,0.5 mm,0.7 mm,0.9 mm时,初相位随初始速度变化的关系。 图6 初相位与初始速度的变化关系Fig.6 Relationship between initial phase and initial velocity 图7是选择A1组骨料、Es=0.01 GPa、砂浆的阻尼系数中取0.02时,初始速度分别为5 m/s,10 m/s,15 m/s,20 m/s,25 m/s时,初相位与初始位移的关系曲线。 图7 初相位与初始位移的变化关系Fig.7 Relationship between initial phase and initial displaceme 图8是选择A1组骨料、Es=0.001 GPa时,初始速度、初始位移与初相位的关系曲线。 图8 初相位与初始位移、初始速度的变化关系Fig.8 Relationship between initial phase and initial displacement and initial velocity 结合韩洁等研究中初始条件对无阻尼自由振动的影响、图5、图6、图7,图8表明:有阻尼自由振动时,初相位与初始位移、初相位与初始速度及三者间的变化趋势,与无阻尼自由振动时的基本一致:初始速度与初相位关系呈非线性,初始位移与初相位的关系呈“类线性”,因此初始速度对初相位的影响比初始位移的大,初始条件既影响振幅,又影响固有频率,也会影响超材料混凝土抗冲击能力。 图9 位移与时间的关系Fig.9 Relationship between displacement and time 图9表明:位移随时间呈周期性变化,初相位随初始速度增加而略有增加;最大振幅随初始速度增加而增加,减幅系数η随初始速度的增大而减小,η60 m/s>η50 m/s>η40 m/s>η30 m/s>η20 m/s;波形不变、振动周期基本不变。 图10 位移与时间的关系Fig.10 Relationship betwee displacement and time 图10表明:位移随时间呈周期性变化,初相位随软涂层弹性模量增加而略减小;减幅系数η随软涂层弹性模量的增大而减小,η0.001 GPa>η0.01 GPa>η0.1 GPa;波形不变、振动周期随软涂层弹性模量的增加而减小。 由式(1)、式(10)、式(15)可知:砂浆弹性模量对位移有较小影响,不同砂浆弹性模量下,位移随时间按正弦规律变化,初相位随砂浆弹性模量增加而略有减小;最大振幅随初始位移增加而增加,减幅系数η随砂浆弹性模量的增大而略有增大;波形不变、振动周期随砂浆弹性模量增大略有减小。 图11 位移与时间的关系Fig.11 Relationship between displacement and time 图示表明:位移随时间呈周期性变化,初相位C3>B2>D4>A1>E5,重核尺寸不变时初相位随软涂层厚度增大而增大;减幅系数ηC3>ηB2>ηD4>ηA1>ηE5,重核尺寸不变时减幅系数随软涂层厚度增大而增大;波形不变、振动周期Td C3>Td B2>Td D4>Td A1>Td E5,重核尺寸不变时振动周期随软涂层厚度增大而增大。 图9、图10、图11可知:减幅系数随阻尼比的增大而增大,随骨料的固有频率增大而减小,因此,设计骨料时,可以通过减小初始速度、增大软涂层弹性模量、增加重核大小等方式降低减幅系数对超材料混凝土结构的影响。 通过理论研究和算例分析,得出如下结论。 (1) 用达朗贝尔原理,导出超材料混凝土单胞骨料的有阻尼三维振动方程,获得固有频率和振动解。 (2)用MATLAB编程计算并结合公式,讨论了初始条件、软涂层和砂浆的弹性模量及骨料几何尺寸等参数对固有频率和振动的影响。结果表明: 固有频率随着软涂层弹性模量的增大而增大,随着软涂层厚度的增大而减小,软涂层对频率有衰减作用,因此可以通过减小重核尺寸、选用弹性模量较大的软涂层材料制作骨料,来提高抗冲击和爆炸荷载的能力,这对超材料混凝土抵抗高频荷载和冲击荷载的研究有工程指导价值。 非线性振动与线性振动中的无阻尼固有频率和有阻尼固有频率的关系并不一致;阻尼对非线性振动系统固有频率的影响,大于线性振动系统。因此,设计骨料时,在保证建筑物符合抗震规范的前提下,要尽可能选择阻尼比小的材料,保证骨料的固有频率,以提高建筑物的抗冲击能力。 有阻尼自由振动时,初始速度与初相位关系呈非线性,初始位移与初相位的关系呈“类线性”,因此初始速度的对初相位的影响大于初始位移,初始条件既影响振幅,又影响固有频率,也会影响超材料混凝土抗冲击能力。 减幅系数随阻尼比的增大而增大,随骨料的固有频率增大而减小,可以通过减小初始速度、增大软涂层弹性模量、增加重核大小等方式降低减幅系数对超材料混凝土结构的影响。
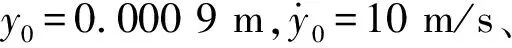



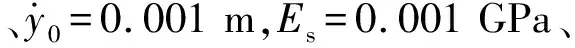
2.3 软涂层弹性模量、骨料几何型号对振动的影响
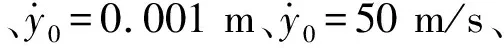

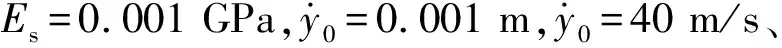
3 结 论

