平面向量核心考点综合演练
■欧阳亮

一、选择题

3.下列说法正确的是( )。
A.单位向量都相等
B.若a∥b,则|a|=|b|
C.若|a|=|b|,则a=b
D.若a=λb(b≠0),则a与b是平行向量

图1



图2

图3

8.(多选题)已知向量a=(2,1),b=(1,-1),c=(m-2,-n),其中m,n均为正数,且(a-b)∥c,下列说法正确的是( )。
A.a与b的夹角为钝角
B.向量a在b方向上的投影为
C.2m+n=4
D.mn的最大值为2
9.(多选题)△ABC中,=b,在下列命题中,是真命题的为( )。
A.若a·b>0,则△ABC为锐角三角形
B.若a·b=0,则△ABC为直角三角形
C.若a·b=c·b,则△ABC为等腰三角形
D.若(a+c-b)·(a+b-c)=0,则△ABC为直角三角形
10.(多选题)已知e1,e2是两个单位向量,λ∈R,|e1+λe2|的最小值为,则下列结论正确的是( )。

11.(多选题)若向量i,j为互相垂直的单位向量,a=i-2j,b=i+mj,且a与b的夹角为锐角,则实数m的取值范围不是( )。

12.(多选题)下列关于平面向量的说法中不正确的是( )。


二、填空题


图4

三、解答题

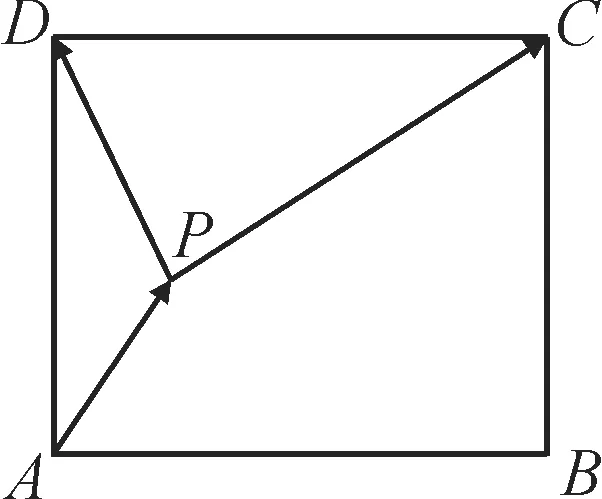
图5

18.已知向量a=(1,2),b=(3,x),c=(2,y),且a∥b,a⊥c。
(1)求向量b与c。
(2)若m=2a-b,n=a+c,求向量m与n的夹角的大小。
19.已知向量a,b的夹角为120°,且=2,c=ma+3b。
(1)当b⊥c时,求实数m的值。
(2)当m=6时,求向量a与c的夹角。
20.已知向量a与向量b的夹角为,且|a|=1,|2a-b|=。
(1)求|b|。
(2)若a⊥(a-λb),求λ的值。
21.已知a,b,c分别是△ABC三个角A,B,C所对的边,且满足acosB+bcosA=。

26.如图6,已知平面四边形ABDC中,满足cos∠ABD=-且cos∠CBD=。

图6
(1)求∠ABC。
(2)若△ABC的外接圆的面积为3π,且,求△ABC的周长。
27.已知△ABC的内角A,B,C的对边分别为a,b,c,且2acosC+c=2b。
(1)若点M在边AC上,且cos∠AMB,求△ABM的面积。
(2)若△ABC为锐角三角形,且b2+c2=a+bc+2,求b+c的取值范围。
参考答案与提示
一、选择题

3.提示:对于A,单位向量的模相等,但方向不一定相同,A 错误。对于B,当a∥b时,其模|a|与|b|可能相等或|a|=λ|b|,λ≥0或|b|=λ|a|,λ≥0,B 错误。对于C,当|a|=|b|且a与b同向时,可得a=b,C错误。对于D,a=λb(b≠0),则a与b是平行向量,D 正确。应选D。


12.提示:由平面向量平行的推论知A 正确。对于B,向量共线,只需两向量方向相同或相反即可,点A,B,C,D不必在同一直线上,B 错误。对于C,由a·c=b·c,可得(a-b)·c=0,则(a-b)⊥c,不一定推出a=b,C 错误。对于D,由平面向量中三角形重心的推论知D 正确。应选B,C。

二、填空题


三、解答题


21.提示:(1)由a=2RsinA,b=2RsinB,c=2RsinC,代入acosB+bcosA=得(sinAcosB+sinBcosA)cosC=sinC·cosA,即sin(A+B)cosC=sinCcosA。因为A+B=π-C,所以sin(A+B)=sinC,所以sinCcosC=sinCcosA。
因为C是△ABC的内角,所以sinC≠0,所以cosC=cosA。又A,C为三角形的内角,所以A=C。





