平面向量中最值问题的常用求法

■田玉帅

平面向量中的最值问题是高考的常考题型，这类问题的常用求法有:函数性质法，基本不等式法，投影法等。下面举例分析，供大家学习与参考。

一、函数性质法

例1如图1，在正方形ABCD中，P为DC边上的动点，设向量则λ＋μ的最大值为_____。

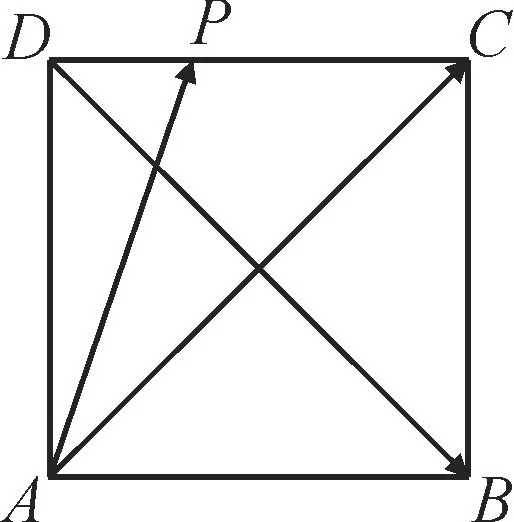
图1

评注：函数y＝（k＞0）在（－∞，0）∪（0，＋∞）上单调递减；函数y＝（k＜0），在（－∞，0）∪（0，＋∞）上单调递增。

二、基本不等式法

图2

三、投影法

评注：向量a在b方向上的投影也可以表示为，投影是一个数量，可正，可负，也可为0，它的符号取决于夹角〈a，b〉的范围。