聚焦共线向量问题

■刘玉成

共线向量也叫平行向量，相等向量是特殊的共线向量。共线向量定理:向量b（b≠0）与a共线，当且仅当存在唯一实数λ，使得a＝λb（b≠0）。

题型1：判断向量共线

例1如图1，四边形ABCD与ABDE是平行四边形。

图1

题型3：用已知向量表示未知向量

例3赵爽是我国古代数学家、天文学家，大约在公元222年，赵爽为《周髀算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”（以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成）。类比“赵爽弦图”，可构造如图2所示的图形，它是由3 个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形，设DF＝2AF，则（ ）。

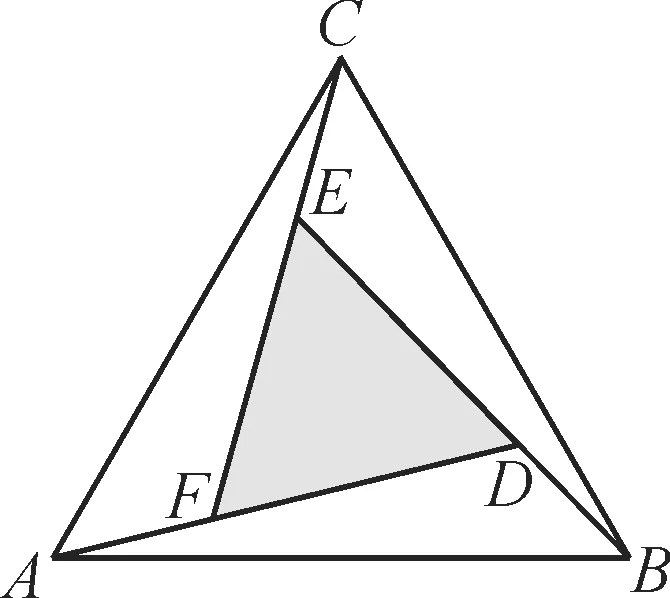
图2

评注：解答本题的关键是理解共线向量与相等向量的含义。

题型2：判断三点共线

评注：用已知向量表示所求向量的实质是向量线性运算的应用。

题型4：根据向量共线求参数的值

（方法2）画出图形，如图3所示。

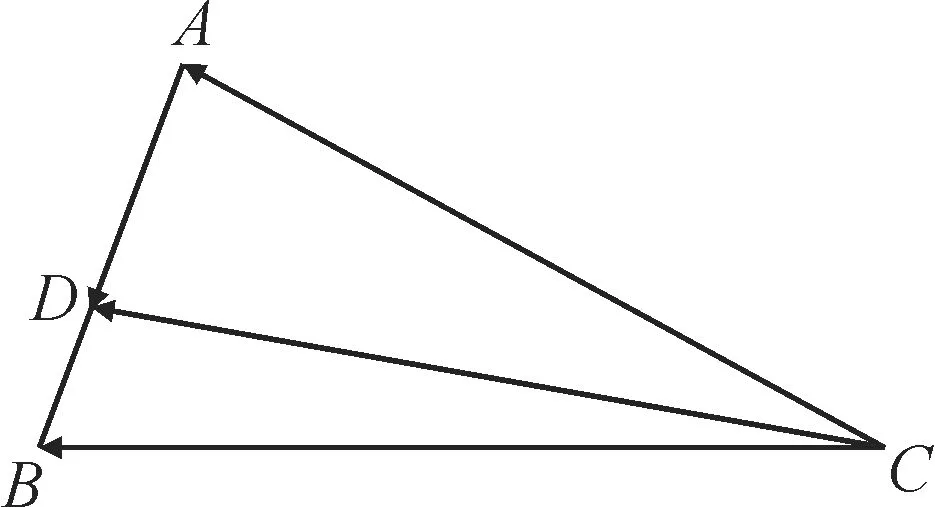
图3

评注：利用共线向量处理求值问题的两种思路:利用共线向量定理a＝λb（b≠0）列方程求解；利用向量平行的坐标表达式x1y2－x2y1＝0求解。

题型5：判断几何图形的形状

评注：两向量共线是两向量相等的必要不充分条件。

题型6：求点的坐标

例6在如图4所示的平面直角坐标系xOy中，点A（4，5），B（1，2），C（12，1），D（11，6），则AC与BD的交点P的坐标为_____。

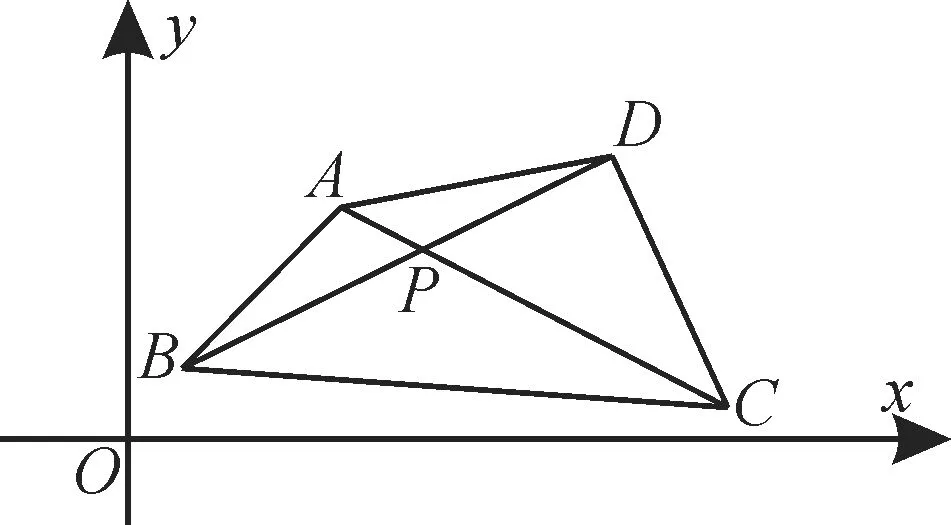
图4

评注：四边形的一条对角线上的三点可以写出6个向量，其中任意两个向量共线。

感悟与提高