基于机器学习算法的高校学生就业去向预测

谷月

(西安航空职业技术学院， 通用航空学院， 陕西， 西安 710089)

0 引言

我国就业压力随高校毕业生数量逐年提升而有所提升，充分分析市场就业形势，预测高校学生就业去向对于缓解我国就业压力具有重要的现实意义[1]。高校学生就业情况具有较高的复杂性以及动态性，通过简单的数据分析方法无法获取高校学生就业的实际情况以及本质，动态、深入研究高校学生就业去向，充分考虑高校学生现实情况利用高效的预测方法实现就业去向分析具有较高实用性[2]。机器学习算法可实现高校学生就业去向精准预测，为高校教育领域以及优化我国就业形式提供有效参考[3-4]。

近年来针对高校学生就业去向预测的研究众多，吕同双等[5]研究基于立体数据的高校学生就业去向预测方法；韦师等[6]研究基于灰色预测模型的我国就业发展趋势分析，分别利用立体数据以及灰色预测模型分析高校学生就业去向以及我国就业发展趋势，可实现高校学生就业去向以及我国就业发展趋势预测，但面对就业去向这一非线性问题预测精度较低，对我国高校学生就业去向分析参考意义较小。

机器学习算法主要包括无监督学习、监督学习以及强化学习3类，贝叶斯分类算法、聚类算法、决策树算法以及支持向量机算法均为机器学习算法中应用较为广泛的高效算法。为了获取更精准的高校学生就业去向预测结果，提出了基于机器学习算法的高校学生就业去向预测方法，并通过仿真平台验证该方法预测有效性，预测结果可为我国高校学生就业情况分析提供参考依据。

1 机器学习算法的高校学生就业去向预测

通过研究大量资料发现，高校学生的就业去向预测与学生的个体人力特征具有很大关联，因此分析高校学生就业相关的数据，可以从个体学业水平、经济条件、家庭背景进行深入研究。基于机器学习算法进行高校学生就业去向预测，主要分为数据采集、数据预处理、生成特征子集和分类预测4个步骤，其流程图如图1所示。

图1 高校学生就业去向预测流程图

机器学习算法的高校学生就业去向预测首先需要采集高校学生就业的相关信息，如受教育年限、个体人力资本特征、个人偏好、预算约束等，将所采集数据实施数据清洗以及数据规约，将完成清洗与规约的数据处理缺失值、异常值实现数据预处理，利用特征选则算法处理完成预处理数据获取最优特征子集[7]，利用最优特征子集建立高校学生就业去向预测数据集，通过机器学习算法的支持向量机算法建立高校学生就业去向预测分类器，将预测数据集发送至支持向量机分类器中，实现高校学生就业去向预测。

1.1 特征选择算法

利用特征选择算法获取最优特征子集，利用最优特征子集建立数据集实现高校学生就业去向预测，特征子集的优劣决定了高校学生就业去向预测精度[8]。从数据集内提取全部特征并用N表示，依据固定规则从特征中获取便于高校学生就业去向预测特征，利用所获取特征建立最优特征子集。用n表示最优特征子集大小，且需满足n≤N。在总特征数量N内选取大小为n的最优特征子集，可能选取的特征子集数量如式(1)，

(1)

特征集合内的特征与特征间可能存在关联性[9]，特征选择算法有效性极为重要。用T={O,F,G}表示原始数据集，其中F={f1,f2,…,fm}与G={g1,g2,…,gm}分别表示特征以及类别，O={o1,o2,…,om}表示原始数据样本集。设置结果评估函数如式(2)，

H:2F→[0,1]

(2)

所获取的H(X)值越高时，表明所获取特征子集X越优，可保留有效特征[10]，且所保留有效特征信息完整度较高。随机选取特征建立特征子集用X表示，设置固定阈值H0，当阈值H大于阈值H0且X最小时完成特征选择。通过以上方法所获取特征子集包含特征数量最少且所包含信息完整度较高。

1.2 支持向量机分类器

支持向量机的基本思想是将输入样本从低维空间利用核函数映射至高维特征空间R内，利用高维空间获取最优分类面，所获取最优分类面可体现输入样本与输出变量间所存在的非线性关系[11]。支持向量机属于凸二次优化问题，可快速获取全局最优解，支持向量机适用于高维模式识别以及非线性问题中，具有较高的推广性能，可应用于函数拟合等问题中。支持向量机分类问题主要包括非线性分类和线性分类两部分。用{(x1,y1),…,(xl,yl)}表示训练样本集，且需满足xi∈Rn，yi∈{-1,1}，i=1,2,…,l。设存在可将两类样本精准区分的最佳分类面，该最佳分类面可令不同分类中间存在较大孔隙[12]，则存在判别函数公式如式(3)：

f(x)=wTx+b

(3)

式中，w表示可确定超平面方向法向量，b表示位移量。

该判别函数相对于全部样本xi均存在f(xi)≥1，可得最佳分类面与样本间最小距离公式如式(4)：

(4)

最佳分类面需正确分类全部样本[13-14]，设置可令全部样本正确分类的约束条件如式(5)：

yi[wTx+b]≥1

(5)

(6)

式中，ai表示拉格朗日系数，且满足ai≥0。

利用拉格朗日函数L获取w与b的最小值，可得公式如式(7)、式(8)：

(7)

(8)

综合以上公式获取优化问题的凸二次对偶形式的最大化公式如下，

(9)

设置式(9)的约束条件如式(10)：

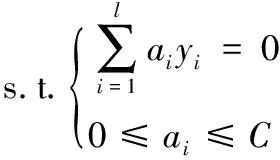
(10)

式中，C表示惩罚参数。

通过以上公式所获取ai中非0样本即支持向量。所获取支持向量分类问题判别式如式(11)：

f(x)=sgn(wTx+b)

(11)

高校学生就业去向预测问题属于非线性问题，需利用非线性映射函数将所采集样本从原有低维空间映射至高维空间内，通过线性可分方法在高维空间内建立最佳分类面[15]，引入松弛变量ξi提升最佳分类面对样本精准分类，将最佳分类面约束转化为式(12)，

yi[wTx+b]≥1-ξi

(12)

非线性分类时的凸二次对偶形式如式(13)，

(13)

式中，K(xi,xj)为核函数。

高校学生就业去向预测问题判别函数为式(14)，

(14)

式中，n表示高校学生就业去向预测问题的支持向量数量。

2 仿真测试

为验证所研究机器学习算法的高校学生就业去向预测有效性，采用MATLAB R2019b软件作为仿真平台，选取某高校2019届毕业生作为实验对象，采集该校2019届毕业生的身份信息、专业成绩、课外实践分数、获取证书等相关数据，所采集数据共18 569条，经过数据清洗等数据预处理后获取有效数据17 524条，将其中的10 000条数据作为支持向量机分类器训练样本，剩余7524条数据作为支持向量机分类器测试样本。

为确定所采用支持向量机分类器最佳参数，统计不同核函数以及惩罚参数情况下支持向量机分类器分类准确率，统计结果如图2所示。图2实验结果可以看出，支持向量机分类器的核函数为径向基函数，惩罚参数值为10时，支持向量机分类器所获取分类精度最高。设置高校学生就业去向预测的核函数为径向基函数，惩罚参数为10。

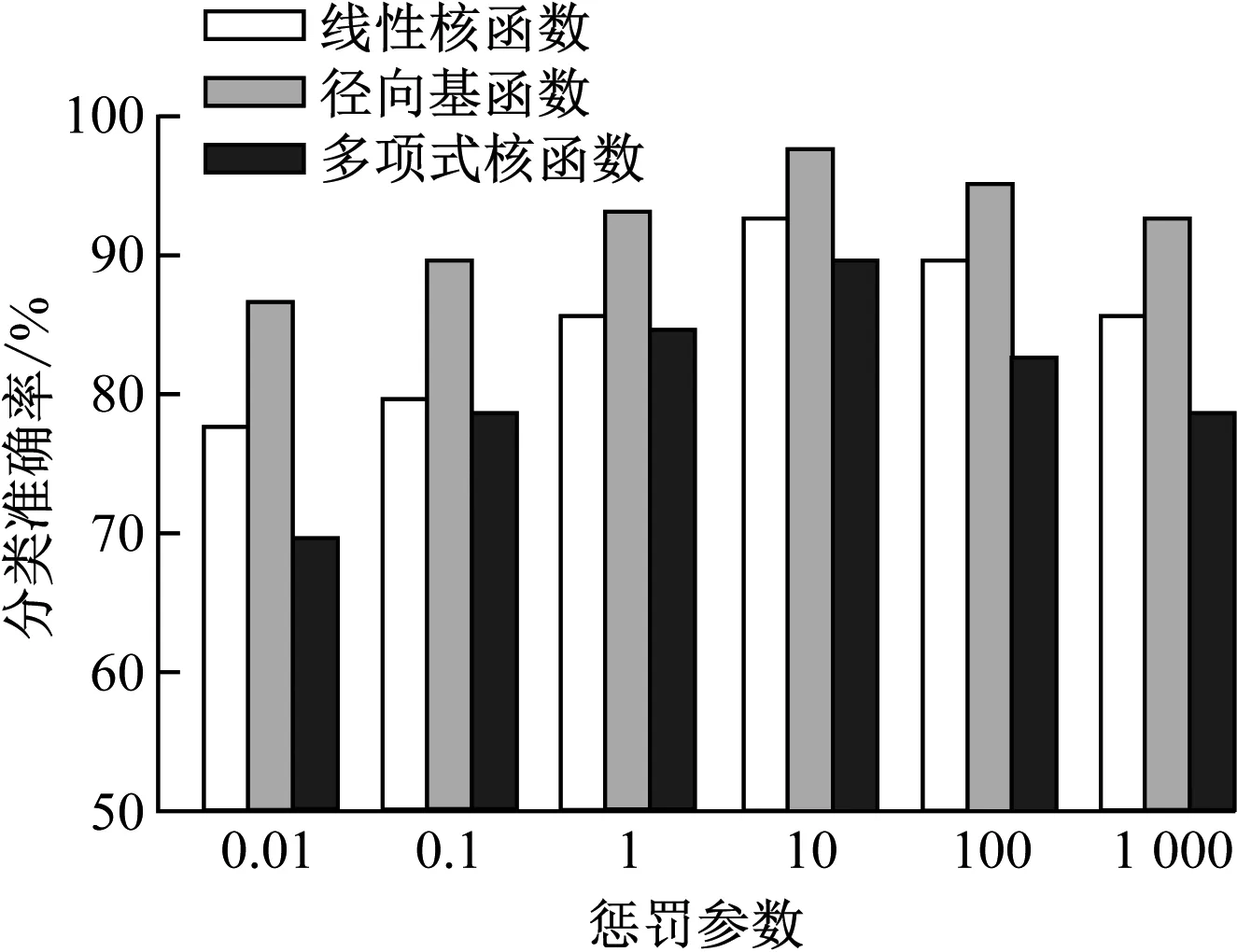
图2 不同参数下分类准确率

采用本研究所设计方法预测该校2019届毕业生不同就业单位性质所占比例，并将预测结果与该校2019届毕业生实际就业单位对比，对比结果如图3所示。

采用本研究所设计方法预测该校2019届毕业生的就业地理区域分布，并将预测结果与该校2019届毕业生实际就业地理区域分布对比，对比结果如图4所示。

从图3、图4实验结果可以看出，采用本研究所设计方法预测该高校2019届毕业生就业单位性质以及地理区域分布与实际毕业生就业单位性质以及地理区域分布结果极为相近，验证采用本研究所设计方法预测高校学生就业去向具有较高有效性。

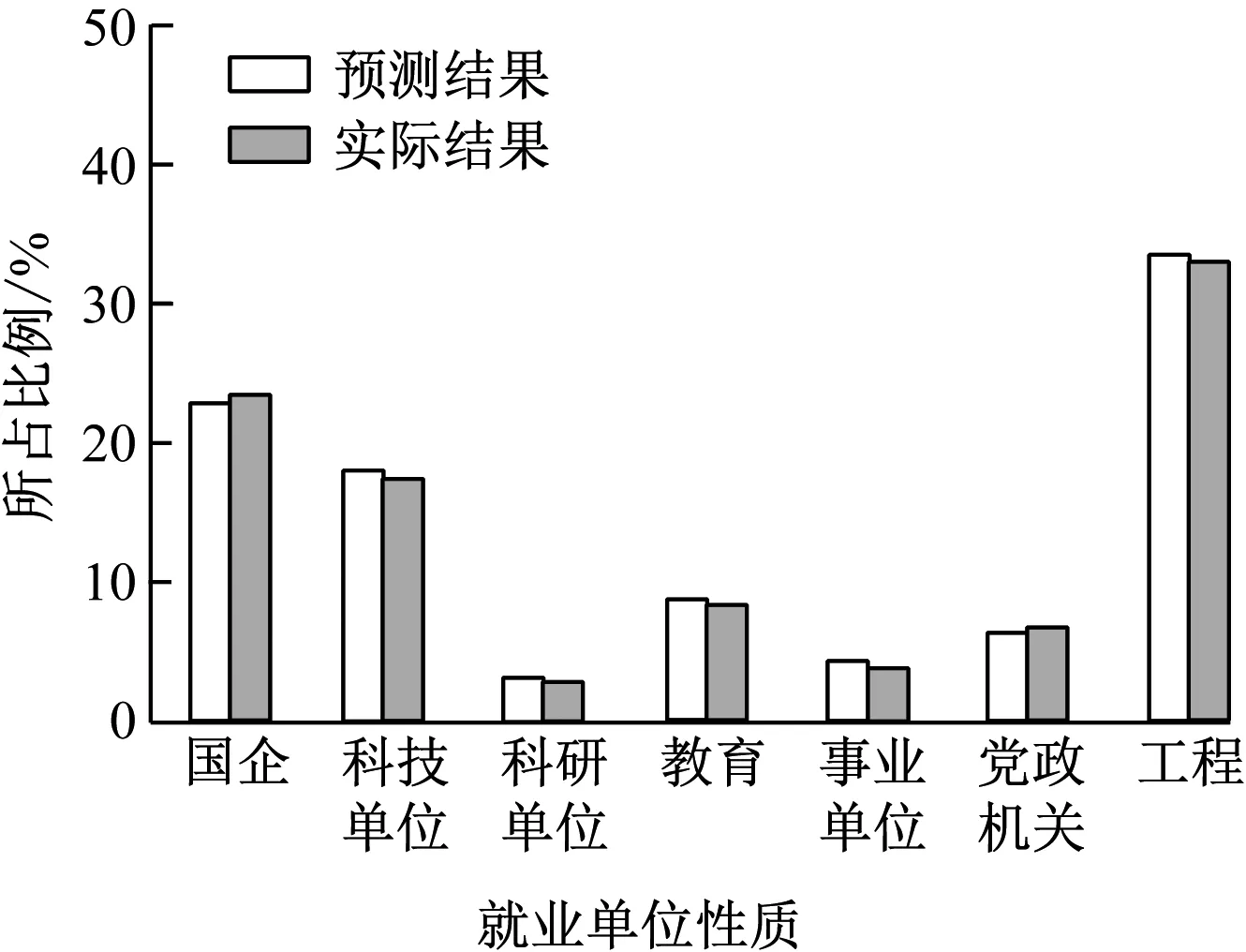
图3 就业单位性质预测结果

图4 地理区域分布预测结果

高校学生就业去向预测是典型的分类任务，利用评估预测性能中常用的预测准确率、预测召回率、F1值以及时间开销作为衡量预测性能的评估指标。将数据集样本以及预测结果分为真正例TP、假正例FP、真负例FN和假负例TN 4类。预测准确率可体现预测正确的样本在实际正例中所占比例，其计算式如式(15)，

(15)

预测召回率可体现预测为正确的正例在应被分类为正例样本中所占比例，其式如式(16)：

(16)

F1值为预测准确率与预测召回率之间的调和平均值，其计算式如式(17)：

(17)

F1值取值区间为[0,1],F1值越高表明预测方法的预测性能越高。

预测时间开销是评价预测性能的重要评价指标，时间开销可体现不同方法的计算速度，选取Python的time.clock统计高校学生毕业去向预测计算时间。

为直观展示本研究所设计方法预测性能，选取文献[5]立体数据方法以及文献[6]灰色预测方法作为对比方法，采用3种方法预测高校学生就业去向的预测准确率、预测召回率、F1值以及时间开销如图5—图8所示。图5—图8各评价指标对比可以看出，不同特征值情况下采用本研究所设计方法预测高校学生就业去向预测准确率与预测召回率均高于98%，不同特征值情况下采用本研究所设计方法预测高校学生就业去向的F1值均高于0.9，不同特征值情况下采用本研究所设计方法预测高校学生就业去向时间开销均低于200 ms。对比结果有效验证采用本研究所设计方法预测高校学生就业去向预测结果相比于另2种方法与实际值更接近，本研究所设计方法的预测效率即时间开销，同样优于另2种方法，说明本研究所设计方法具有优越的预测性能。

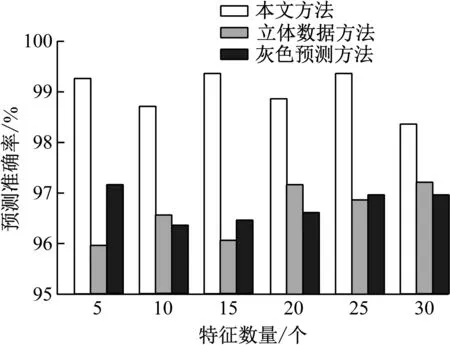
图5 预测准确率对比结果

图6 预测召回率对比结果

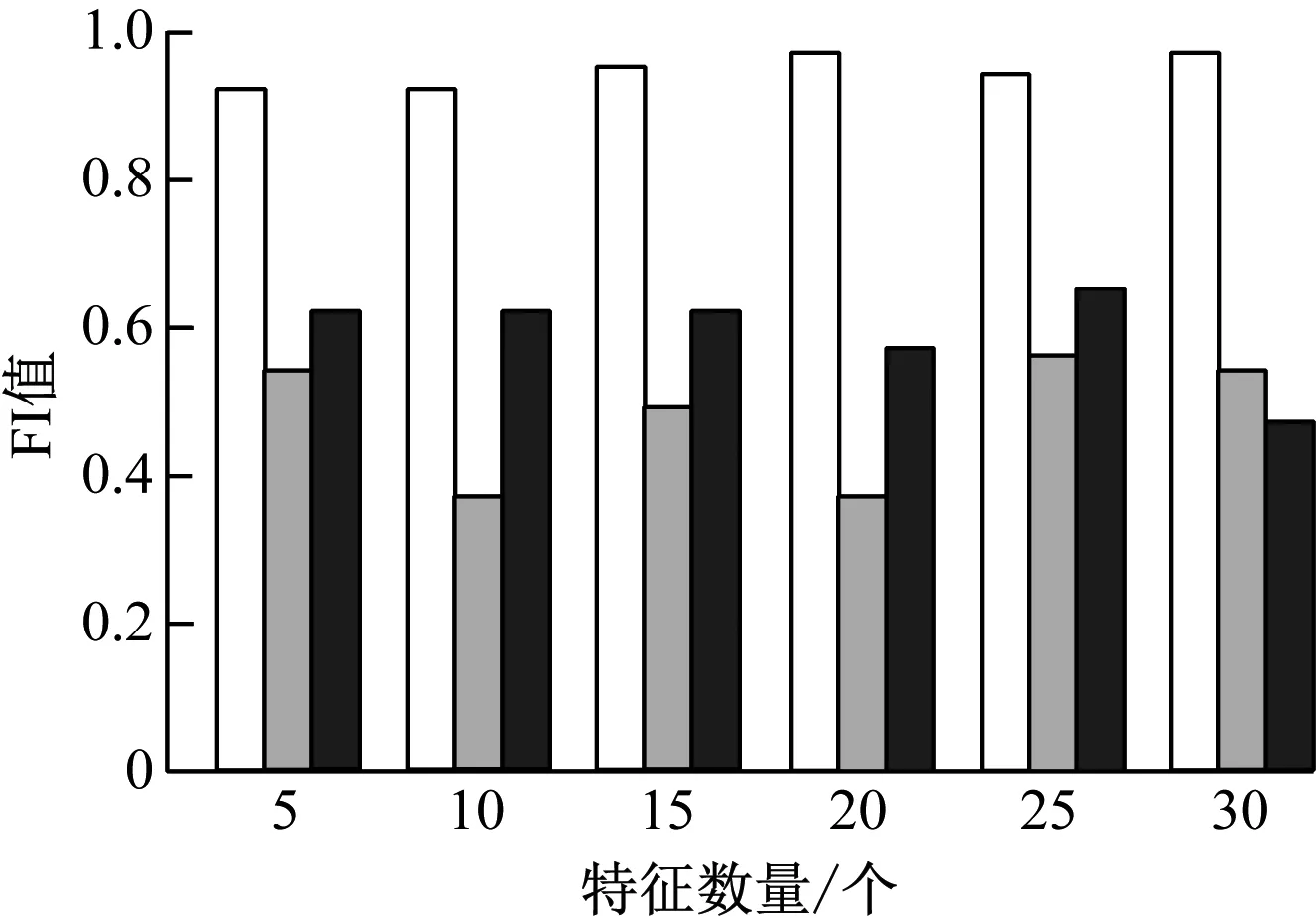
图7 F1值对比结果

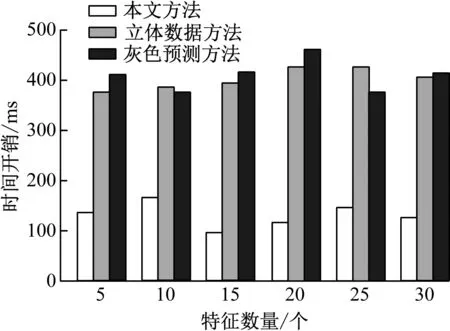
图8 时间开销对比结果

3 总结

采用机器学习算法预测高校学生就业去向，有助于客观、全面分析高校学生毕业后就业去向，为缓解社会就业压力以及高校分析学生毕业动向提供良好依据。机器学习算法具有较高的灵活性，将机器学习算法应用于高校就业去向预测，通过增加变量可提升机器学习算法准确性以及高效性，可以为提升高校教育水平以及社会就业服务提供理论依据。但本文研究所设计方法仅选择了一所学校的一届毕业生的数据进行验证，所得出的结论未必能够适用于国内其他的高校，且数据的来源是行政部门提供的学生数据，对于学生的心理偏好、家庭背景等未进行深入调研，在未来的研究中，可以考虑选取国内多地区的高校学生数据，以及对个体进行深入调查，以进一步提升设计方法的预测精准度。