因子分析和神经网络的信息系统风险评估模型
胥林
(中国石油化工股份有限公司胜利油田分公司, 信息化管理中心, 山东, 东营 257000)
0 引言
随着信息技术、软件技术和网络技术的快速发展,政府、企业等的信息化程度越来越高,信息管理系统应用日益广泛[1-3]。但是由于信息管理系统的开放性和网络的不设防性,同时出现了信息安全问题,几乎所有的信息管理系统都存在不同程度的风险,而信息系统风险评估可以帮助政府、企业的信息管理人员了解风险的变化规律,制定相应的信息系统风险控制措施,因此如何设计性能优异的信息系统风险评估模型是人们关注的焦点[4-6]。
信息系统风险的评价指标多,指标互相影响,又互相关联,使得信息系统风险变化比较复杂[7],当前有学者提出基于多种类型的信息系统风险评估模型,得到了有效的评估结果,为降低信息系统风险做出了很大贡献[8-10]。然在实际应用中,这些方法均存在不足,如评估误差大、耗费时间长、工作效极率低,同时它们没有区分指标之间差异性,假设所有指标作用相同,使得信息系统风险评估正确不高,信息系统风险评估的效率低下[11-12]。
针对当前信息系统风险评估过程中的指标选择问题和建模方法选择问题,为了改善信息系统风险评估效果,提出了因子分析法和RBF神经网络相融合的信息系统风险评估模型,并进行了指标筛选,减少了指标维量,简化RBF神经网络的复杂度,并采用蚁群算法对RBF神经网络进行优化,提升RBF神经网络的学习效率,大幅度提升信息系统风险评估正确率,为信息系统风险分析和评估提供了新的研究思路。
1 本文设计的信息系统风险评估模型
1.1 设计信息系统风险评估的指标体系
信息系统风险与多种因素密切相关,同时多种因素会共同产生风险作用,因此信息系统风险形式十分复杂,很难有一定的规律,同时具有一定的随机性。在进行信息系统风险变化规律建模与评估时,首先要设计科学、客观的信息系统风险评估指标体系。本文基于科学性、可操作性、区分性、全面性的原则,设计了指标体系如表1所示。

表1 信息系统风险评估指标体系
1.2 因子分析法
从表1可以看出,信息系统风险评估的指标数量比较多,这些指标之间有直接相关性或者间接相关性,这些相关性以重复信息显示,这些重复信息不仅会对信息系统风险评估产生一定的干扰,指标多,全部用于风险评估,耗长长、效率低,所以采用因子分析法对指标进行筛选,减少指标数量。设共有k个指标,指标量纲不同,使得它们的值差异比较大,影响RBF神经网络学习时的收敛效率,为此对其进行预处理,具体如式(1):
(1)
式中,xxi表示信息系统风险评估指标的原始值,xi表示处理后的信息系统风险评估指标值。
因子分析法用m(m (2) 式中,ei表示特殊因子,fi表示公共因子,aij表示公共因子的负载。 用矩阵形式表示式(2),得到式(3), X=AF+ε (3) 其中 (4) 为了对式(3)进行求解可以将式(3)转化为式(5): (5) (6) 根据式(6)得到指标公共因子值,从而得到风险评估指标数量[13]。 X=[x1,x2,…,xn]T为输入向量,径向基向量为H=[h1,h1,…,h6]T,则有式(7), (7) 式中,Cj=[cj1,cj2,…,cjn]为节点j的中心矢量,且有式(8)[14]: cji(k)=cji(k-1)+ηΔcji+α(cji(k-1)-…-cji(k-p)) (8) 式中,η为学习速率,α为动量因子,且有式(9), (9) 式中,bj为基宽参数。 网络的权向量为W=[w1,w1,…]T,那么有式(10): (10) RBF神经网络网络的输出为式(11), ym(k)=w1h1+w2h2+…+wphp (11) 将因子分析法、RBF神经网络、蚁群算法[15]进行结合,利用它们的优势,克服当前信息系统风险评估模型存在的不足,本文设计了一种新型的信息系统风险评估模型,具体工作过程如下。 Step1:分析信息系统的工作流程,以及变化特点,建立风险指标体系。 Step2:采集相应指标数据,并对一些错误的数据点进行去除,保证信息系统风险评估性能。 Step3:采用因子分析法对信息系统风险评估指标进行处理,去除一些不重要的数据,选择最优指标,消除无用信息。 Step4:专家根据每一组信息系统风险评估指标值对每一个样本进行打分,得到信息系统风险值。 Step5:风险值和对应的信息系统风险评估指标数据组合成样本集合,并将它们划分为训练样本和测试样本。 Step6:采用信息系统风险评估的训练样本训练RBF神经网络,通过蚁群算法优化RBF神经网络的相关参数。 Step7:根据相关参数建立信息系统风险评估模型,流程如图1所示。 为了分析本文设计的信息系统风险评估的有效性和优越性,收集一个信息系统风险变化的历史值,同时采集表1中的信息系统风险评估指标的数据,信息系统风险的历史数据如图2所示。对图2的信息系统风险的历史数据进行分析可以发现,不同时间点,该信息系统风险值之间有一定的相似性,但是有的信息系统风险值差别比较大,具有很强的非平稳性,采用MATLAB工具箱编程实现信息系统风险的仿真实验。 图1 因子分析和神经网络的信息系统风险评估流程 图2 信息系统风险的历史数据变化趋势 采用因子分析法对指标进行分析,得到指标累积贡献率如图3所示。从图3的信息系统风险评估指标的累积贡献率可以发现,前8个因子的累积贡献率就超过了95%,这表明前8个因子就可以代表原始信息系统风险评估指标,可以去掉其它对信息系统风险评估结果影响不明显的因子。 图3 信息系统风险评估指标的累积贡献率 为验证使因子分析法和神经网络的信息系统风险评估结果具有可比性,采用神经网络、层次分析法作为对比方法,为避免信息系统风险评估结果的随机性,选择不同数量的训练样本进行信息系统风险评估测试,评估正确率如图4所示。从图4可知,随着训练样本数量的增加,信息系统风险评估正确率不断的提升,这是因为训练样本数量越多,信息系统风险评估建模更加充分,在相同训练样本数量条件下,本文模型的信息系统风险评估正确率要高于对比方法,可以更好地描述信息系统风险变化规律。 图4 3种模型的信息系统风险评估正确率对比 为了更好地描述信息系统风险评估的实时性,选取训练样本和测试样本数量为1∶1的条件下,3种模型的信息系统风险评估训练和测试时间如图5所示。从图5可以发现,本文模型的信息系统风险评估训练和测试时间要少于对比模型,提高了信息系统风险评估速度。 图5 3种模型的训练和测试时间对比 当信息系统风险评估的指标比较多时,指标间信息重复度大,重复信息干扰了评估结果,为了更加准确描述信息系统风险的变化特点,提出了因子分析和神经网络的信息系统风险评估模型,并通过具体仿真测试得到了如下结论。 (1) 采用因子分析方法选择对信息系统风险评估作用大的评估指标,可以降低RBF神经网络的输入层节点数量,简化RBF神经网络的结构,能够提高信息系统风险评估效率。 (2) RBF神经网络拟合信息系统风险变化趋势,可以建立正确率高的信息系统风险评估模型。 (3) 通过与其它信息系统风险评估模型进行比较测试可以知道,本文模型的信息系统风险评估正确率更高,降低了信息系统风险评估误差而且信息系统风险评估速度更快,具有十分明显的优越性。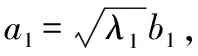
1.3 RBF神经网络
1.4 信息系统风险评估模型具体设计
2 因子分析和神经网络的信息系统风险评估模型的性能验证实验
2.1 实验数据


2.2 因子分析法对信息系统风险评估处理的结果

2.3 不同模型的信息系统风险评估正确率和建模效率对比


3 总结

