基于历史数据驱动的运动员成绩估计研究

马超

(东北石油大学， 体育部， 河北， 秦皇岛 066000)

0 引言

运动员是国家体育发展的重要储备力量，准确估计运动员成绩，能够为其制定更适用的训练规划，提升其成绩[1-3]。训练强度与运动员自身身体素质等因素可直接影响运动员成绩，只有精准了解运动员成绩的变化特点，才能确保运动员取得更好的成绩[4]，这就说明估计运动员成绩非常重要。陈曦等[5]研究融合知识图谱和协同过滤的学生成绩预测方法，建立描绘课程信息的课程知识图谱，通过基于邻节点方法与基于知识图谱学习方法计算课程在知识层面的相似度，将获取的相似度集成到协同过滤的成绩预测框架，获取成绩预测结果；李梦莹等[6]研究基于双路注意力机制的学生成绩预测模型，通过两次注意力计算获取不同属性特征在第一阶段与第二阶段成绩上的注意力得分，结合多特征融合方式，获取成绩预测结果。基于历史数据驱动的预测方法是通过历史数据实施预测[7-8]，基于历史数据驱动的预测方法有很多，例如隐马尔科夫模型、混沌预测与支持向量机等。支持向量机存在小样本学习与学习能力强的优点，在预测方面具有一定优势，因此用来研究基于历史数据驱动的运动员成绩估计方法。利用KNN算法对运动员的历史成绩进行预处理，去除干扰数据的影响，精准地对数据进行了分类；利用支持向量机构建回归预测模型，引入拉格朗日函数进行数据转换，以避免数据运算陷入局部；利用粒子群算法对支持向量回归预测模型参数进行优化，减少输入量噪声的干扰，降低计算的复杂度。

1 基于历史数据驱动的运动员成绩估计方法

历史数据驱动估计运动员成绩估计思想：首先数据预处理，因为原始运动员历史成绩数据集内会存在噪声干扰，支持向量回归不能直接通过原始运动员历史成绩数据集实施估计，所以利用K最近邻(K-nearest neighbor，KNN)分类算法实施数据预处理；然后将数据预处理后的运动员历史成绩数据集作为支持向量回归预测模型的训练样本，经过支持向量回归预测模型训练后，获取运动员成绩估计结果；最后利用粒子群算法优化支持向量回归参数，提升估计结果的准确性。

1.1 数据预处理

运动员历史成绩数据包含各赛级的比赛名次、比赛运动用时、年龄、性别、训练时长、体质。利用KNN算法对运动员历史成绩数据实施数据预处理[9]，减少不完整数据信息的干扰，无需先验统计即可实现数据的分类。KNN算法的核心思想是假设在运动员历史成绩特征空间内，若一个运动员历史成绩样本的k个最邻近运动员历史成绩样本内的多数属于某一个类别，则判断这个运动员历史成绩样本也属于这个类别，同时存在这个类别运动员历史成绩样本的特性。KNN算法的具体步骤如下。

步骤1：建立运动员历史成绩训练样本集T。

步骤2：设置k的初始值。

步骤3：在运动员历史成绩训练样本集内选取和运动员历史成绩测试样本最接近的前k个样本，利用欧几里德距离获取运动员历史成绩样本X与Y的相似度，欧几里德距离计算如式(1)，

(1)

假设全部运动员历史成绩样本属于n维空间Rn，任一运动员历史成绩样本Xi=xi1,xi2,…,xin∈Rn，其中第i个运动员历史成绩样本的第k个特征值是xik。运动员历史成绩样本Xi与Xj的欧几里德距离是dXi,Xj，dXi,Xj用来表示运动员历史成绩样本的相似度。计算式如式(2)：

(2)

式中，第j个运动员历史成绩样本的第k个特征值是yjk。

步骤4：针对运动员历史成绩测试样本Xq，和Xq距离最近的k个运动员历史成绩样本是X1,…,Xk，假设离散点目标函数是F:Rn→ei，第i个类别标签是ei，标签集合是E=e1,…,es>。离散点目标函数计算式如式(3)：

(3)

式中，返回值是s，运动员历史成绩样本间的相似度是δ，当样本a与样本b一致时，δa,b=1，当样本a与样本b不同时，δa,b=0。

步骤5：将投票数量多的运动员历史成绩样本作为支持向量机的输入。

1.2 支持向量回归预测模型

利用支持向量回归预测模型估计运动员成绩，支持向量回归估计模型属于在高维特征空间内构建回归预测函数；将数据预处理后的运动员历史成绩数据集作为支持向量回归预测模型的输入；线性回归不敏感损失函数ε的计算式如式(4)：

(4)

式中，f(x)为支持向量机的回归预测函数，l为实际值。

回归函数的对应值就是运动员成绩估计值，因此获取最优化计算式如式(5)：

(5)

(6)

整理式(6)后可得式(7)，

(7)

高斯核函数计算式如式(8)：

(8)

式中，σ为高斯核带宽，σ>0。

支持向量回归预测模型的预测函数为式(9)：

(9)

1.3 粒子群优化支持向量回归参数

支持向量回归预测模型中惩罚因子C、高斯核带宽σ与不敏感损失函数ε的取值与估计精度关系紧密。惩罚因子C的取值和能够允许的误差有关，C值与允许误差成反比；高斯核带宽σ和训练样本的输入空间范围成正比，一般情况下，高斯核带宽σ取值相对大一些；不敏感损失函数ε和输入量噪声大小有关，输入量噪声较小时，不敏感损失函数ε取值相对小一些;输入量噪声较大时，不敏感损失函数ε取值相对大一些。利用粒子群算法优化支持向量回归预测模型的惩罚因子C、高斯核带宽σ与不敏感损失函数ε，将空间向量C,σ,ε当成粒子群算法内的一个粒子，利用算法迭代获取最优粒子，支持向量回归预测模型在当前训练样本数据下的最优参数分别是xq,C、xq,σ与xq,ε，粒子群算法优化支持向量回归预测模型参数的具体步骤如下。

步骤1：初始化支持向量回归预测模型参数，设置最大迭代次数是Gmax；粒子位置的限定范围是Xmin,C,Xmax,CXmin,σ,Xmax,σXmin,ε,Xmax,ε；粒子速度的限定范围是[-Vmax,C,Vmax,C][-Vmax,σ,Vmax,σ][-Vmax,ε,Vmax,ε]；粒子种群规模是M；随机设置粒子速度与位置，粒子q的位置是xq,C,xq,σ,xq,ε，惩罚因子C值大小是xq,C，高斯核带宽σ值大小是xq,σ，不敏感损失函数ε值大小是xq,ε，粒子q的速度是vq,C,vq,σ,vq,ε；

步骤2：将xq,C,xq,σ,xq,ε当成参数训练支持向量回归预测模型，交叉验证支持向量回归预测模型估计精度当成适应度值，假设待估计的样本数是t，利用均方误差衡量支持向量回归预测模型内参数的适应度，均方差MSE的计算式如式(10)，

(10)

步骤3：粒子q个体通过的最佳位置是pbestq=pq,C,pq,σ,pq,ε，记录粒子q的MSE值最小的位置信息是pbestq；

步骤4：种群通过的最佳位置是gbest=gC,gσ,gε，记录群体全部粒子在迭代时的最小MSE值相应的位置信息是gbest；

步骤5：假设粒子位置与速度均大于设定区间，那么选择边界值限制粒子速度与位置，粒子位置xq与速度vq的更新式如式(11)、式(12)，

(11)

(12)

式中，γ为迭代次数，ω为惯性因子，c1与c2为学习因子，r1与r2为加速常数。

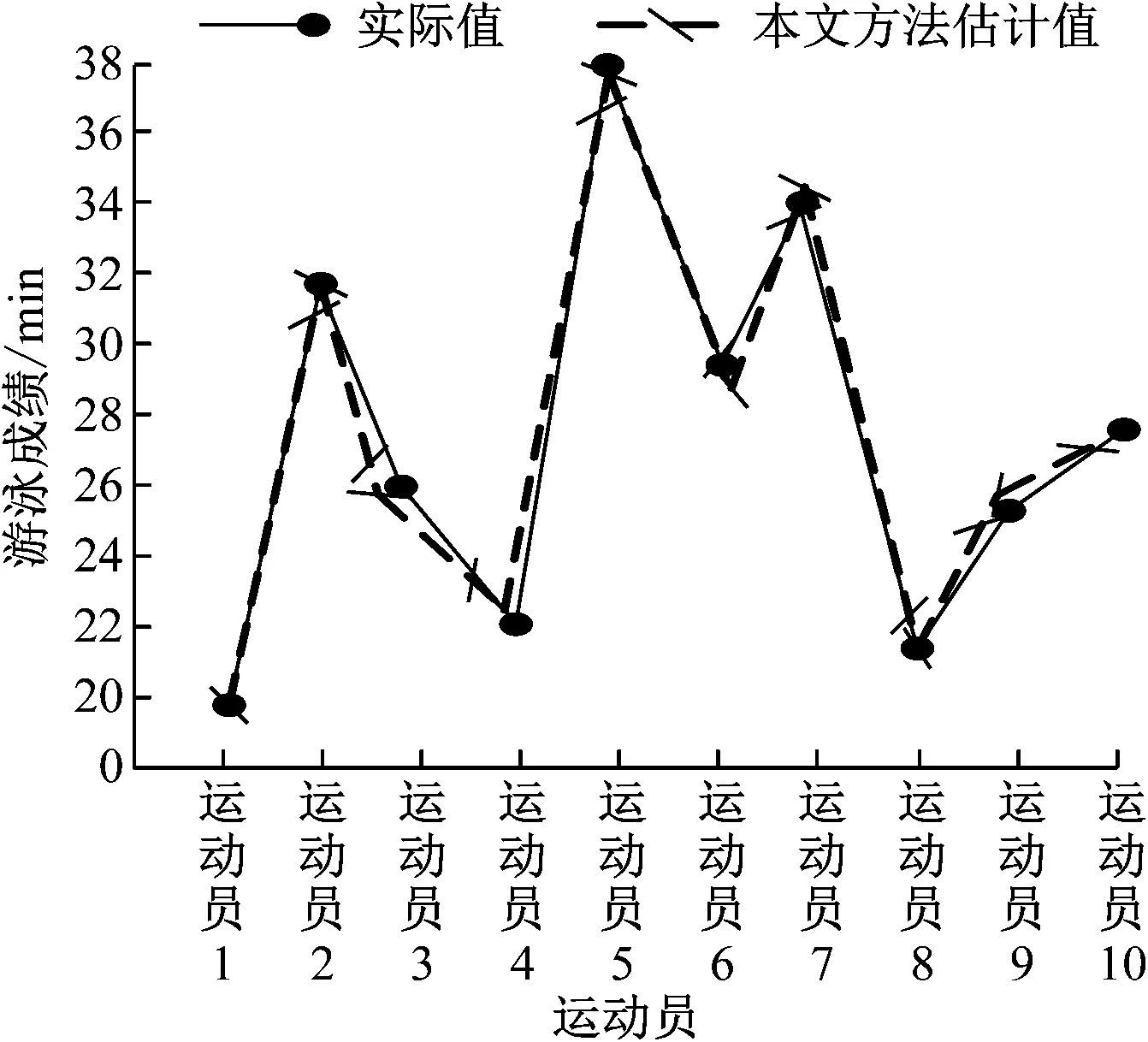
步骤6：如果迭代次数γ

2 实验结果分析

以某体育学校的运动员为实验对象，随机选取10组1500 m自由泳运动员作为研究对象，每组10人，利用本文方法对这10组游泳运动员成绩实施估计，估计结果如图1所示。根据图1可知，本文方法能够有效估计出游泳运动员的成绩，且估计值与实际值非常接近。实验证明：本文方法能够精准估计运动员成绩，具有较高精度的运动员成绩估计结果。

图1 10组运动员游泳成绩估计结果

在该校内随机选取10种类型运动项目的运动员，验证本文方法的通用性，利用本文方法对这10种运动项目的运动员成绩实施估计，并与实际值对比，10种运动项目的估计精度如图2所示。根据图2可知，针对不同类型的运动项目，本文方法均能准确估计运动员的成绩，估计精度基本维持在96%以上。实验证明：本文方法具有很好的通用性，且估计精度高。

图2 10种运动项目成绩的估计精度

利用本文方法与方法1、方法2同时对上述10种类型的运动项目的运动员成绩实施估计，测试3种方法的估计精度与估计效率，其中方法1为融合知识图谱和协同过滤的学生成绩预测方法(文献[5])，方法2为基于双路注意力机制的学生成绩预测模型(文献[6])，每种运动项目选取100名运动员的成绩进行测试，取其平均值，提升实验的可信度，3种方法对10种类型运动项目的运动员成绩估计精度与估计效率如图3、图4所示。根据图3可知，针对不同类型运动项目的运动员，本文方法的运动员成绩估计精度明显高于其余2种方法，本文方法的平均估计精度是97.8%，方法1的平均估计精度是81.9%，方法2的平均估计精度是86.6%。实验证明：估计不同类型运动项目的运动员成绩时，本文方法的估计精度最高，明显降低运动员成绩估计误差，同时增加估计结果可信度。根据图4可知，针对不同类型运动项目的运动员，本文方法的运动员成绩估计时间明显低于其余2种方法，本文方法的估计时间始终维持在20 s以内，变化幅度较小，其余2种方法的估计时间变化幅度较大，稳定性较差。实验证明：本文方法的估计时间最少，运动员成绩估计效率更高。

图3 3种方法的估计精度

图4 3种方法的估计效率

以1500 m游泳运动员成绩为例，测试3种方法在不同运动员数量时，成绩估计的准确性，通过误差评价指标平均绝对百分误差(Mean Absolute Percentage Error，MAPE)对3种方法的性能实施准确性评估，在不同运动员数量时，3种方法的误差评价指标测试结果如图5所示。根据图5可知，随着运动员数量的不断增加，3种方法的MAPE值均随之提升，一般情况下，MAPE值低于10，说明估计方法的估计精度较高，在不同运动员数量时，本文方法的MAPE值均明显低于其余两种方法，MAPE值始终保持在10以内，其余2种方法只有在运动员数量低于200人时，MAPE值低于10；当运动员数量超过200人时，2种方法的MAPE值均大于10。实验证明：在不同运动员数量时，本文方法的MAPE值最低，说明本文方法的估计值与实际值最为接近，估计精度更高，估计质量高。

图5 3种方法的误差评价指标对比图

3 总结

本文方法实现高质量的运动员成绩预测，对于运动员的训练规划非常重要，精准估计运动员成绩，能够了解其所需要的训练规划，利于提高运动员成绩，使其更加优秀；因此研究基于历史数据驱动的运动员成绩估计方法，提升运动员成绩估计精度与估计效率，为运动员训练规划提供更有价值的信息，为国家培养更为优秀的运动员。