非等时距灰色模型在建筑物沉降预测中的应用*
崔 伟,张绪涛,阮兴群,孟凡涛
(1.聊城大学建筑工程学院,山东 聊城 252000;2.山东华科规划建筑设计有限公司,山东 聊城 252000)
0 引言
沉降监测和预测是保证建筑物安全质量的重要方式[1-3]。当今我国城市化建设快速推进,尤其是高层建筑拔地而起,但是随着建筑物高度不断增加、荷载不断加大以及监测预测分析未能及时跟进,造成了大量工程事故[4]。为此把握地基沉降发展规律并进行沉降预测有非常重要的意义[5]。国内学者对于建筑物沉降预测进行了大量研究:陈威等[6]将三点法与灰色模型(grey model,GM)相组合进行路基沉降预测,结果表明该方法可较好地用于路基沉降预测;姜献东等[7]将灰色系统理论应用于软基沉降预测;单瑞等[8]通过牛顿插值平均法与泊松曲线相结合的方式应用于高层建筑沉降预测中,结果表明泊松曲线预测与实际沉降预测曲线吻合性较好,拟合精度较高;刘光秀等[9]通过建立灰色-Gompertz组合模型,对高速公路软土路基进行沉降预测分析,取得了良好效果。但是,目前建立的建筑物沉降预测模型大多算法繁杂不易实现,进而影响工程实际应用。
为提高预测模型的序列应用性和预测结果的可靠性,满足工程实际应用,引入组合思维,根据聊城市昌润祥荷园8号楼实测数据,通过三次样条插值和灰色模型相结合,建立起非等时距灰色模型,将实测数据与预测数据对比分析,验证本文方法的可行性,并采用控制变量法,对时间间隔和观测次数两种因素进行了精度分析,为构建高精度预测模型提供借鉴。
1 非等时距灰色模型
1.1 三次样条插值法下的等时距数据转化
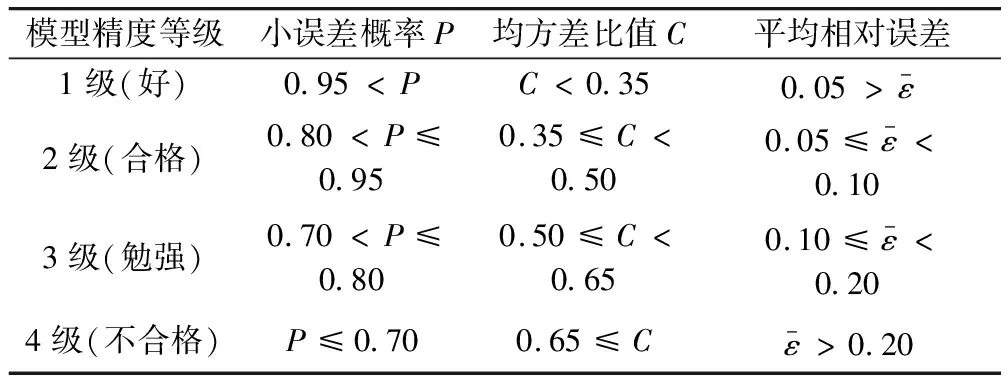
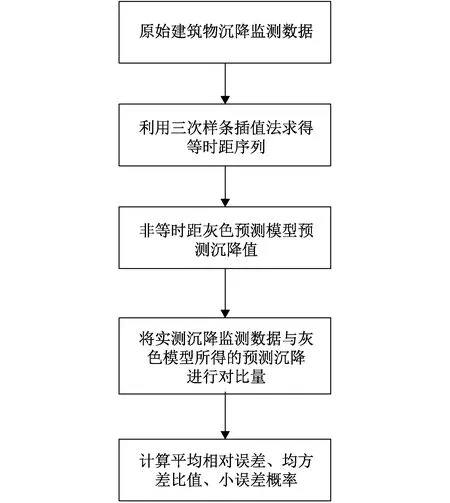
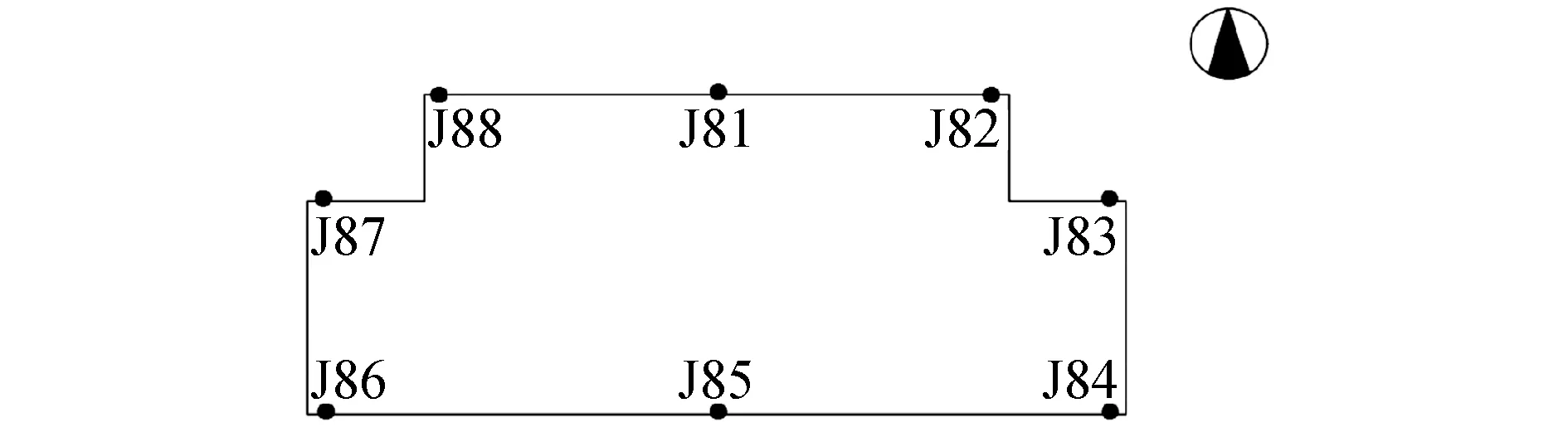
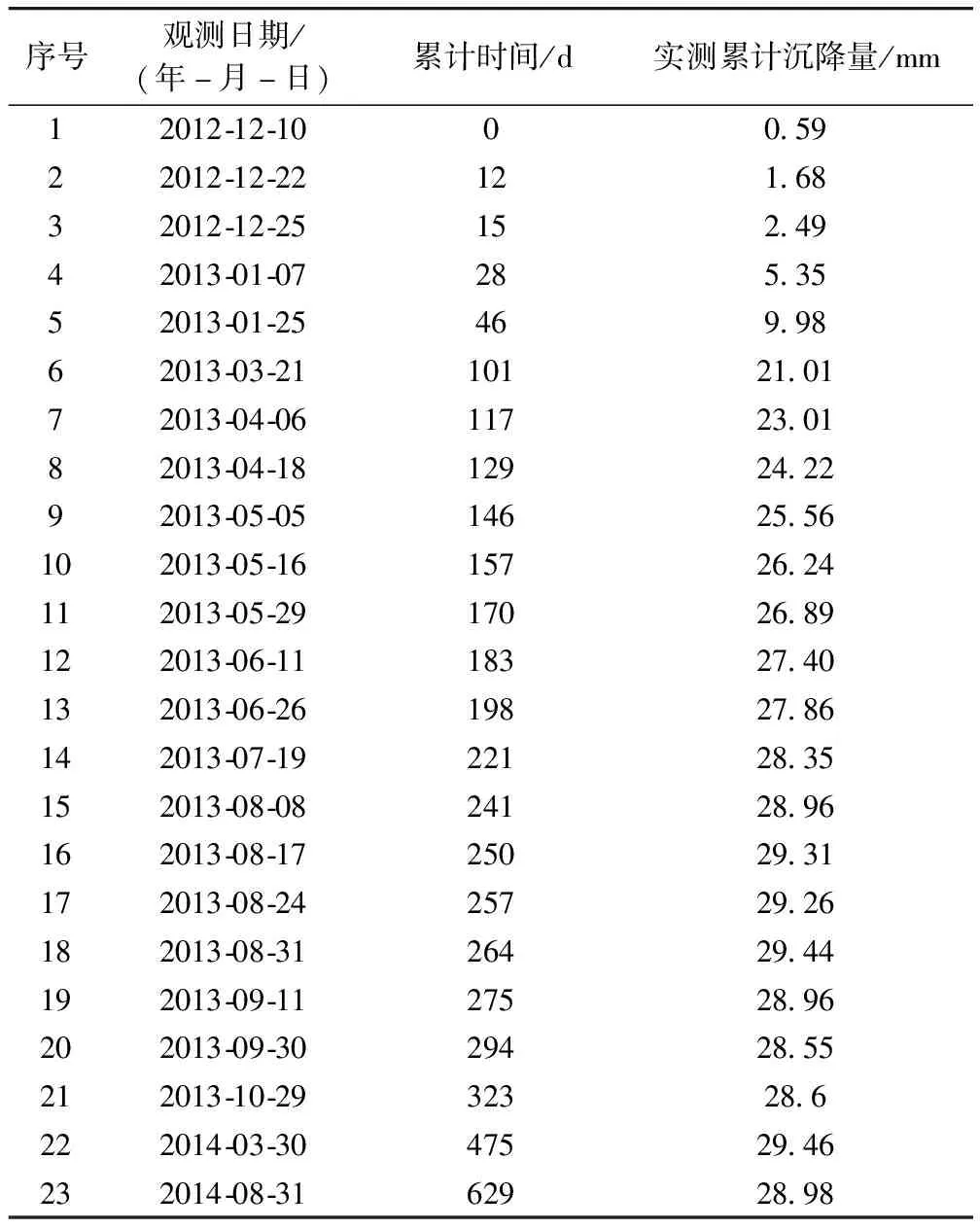
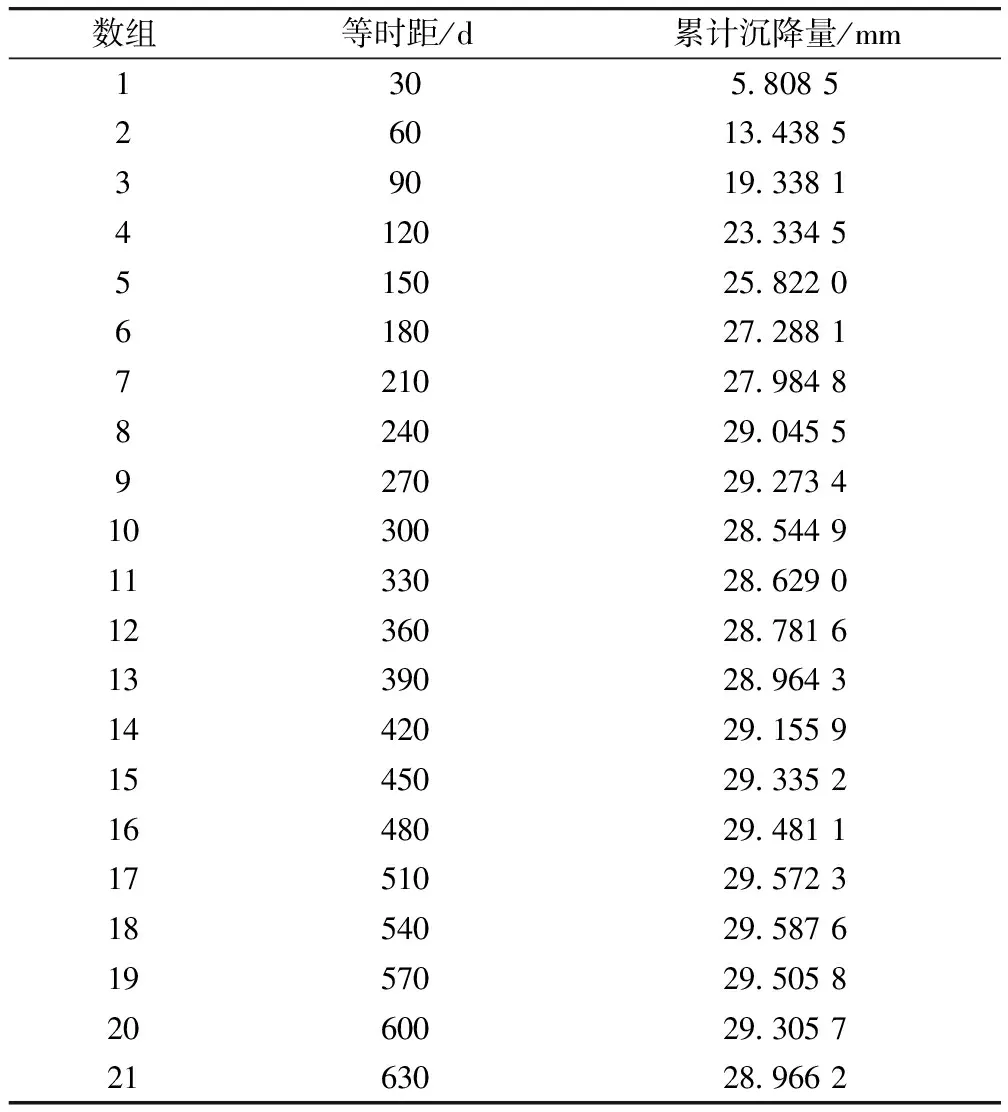
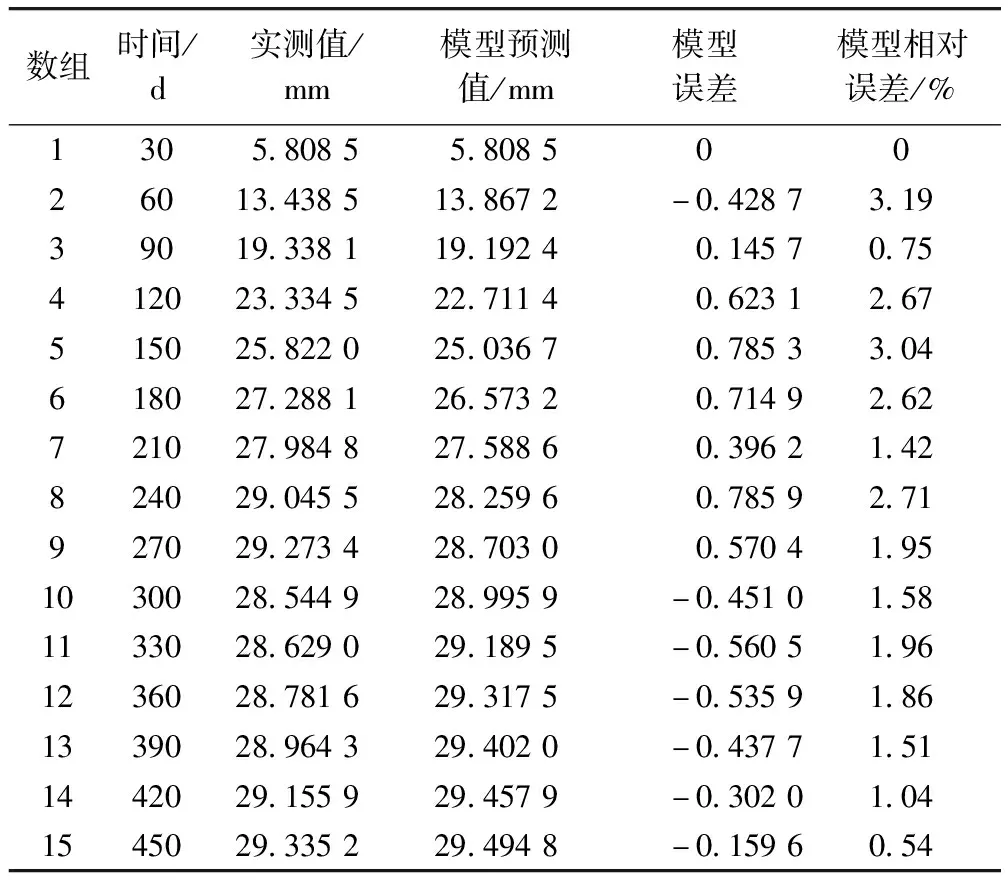
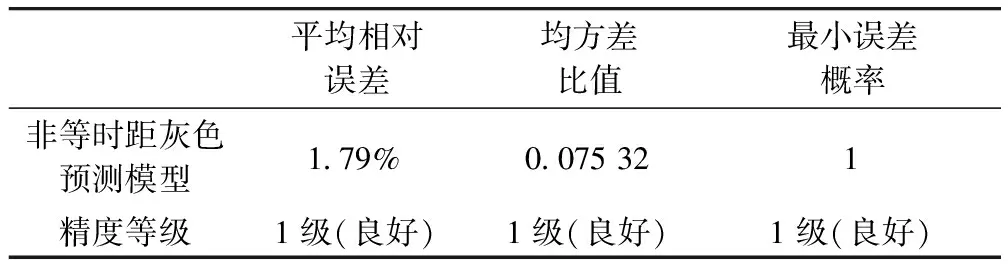
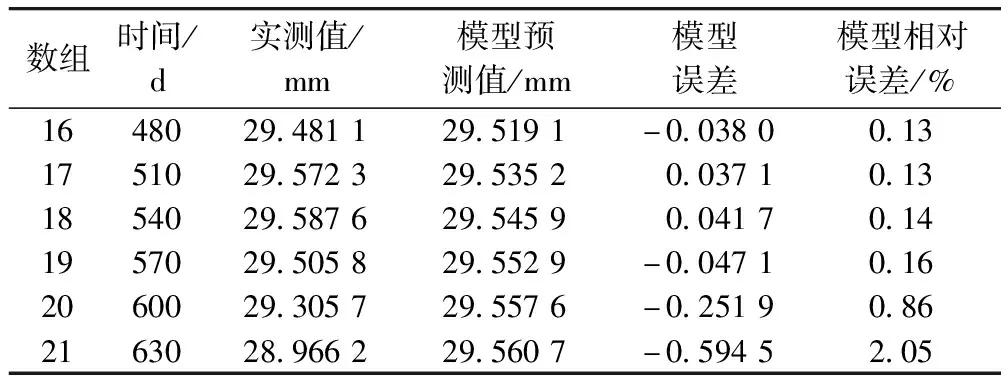
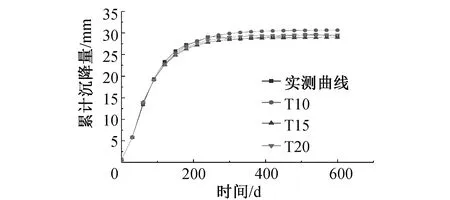
三次样条插值[10]是依据数学方法,在样点之间进行插值估算,生成平滑曲线的方法。其数学定义如下:若函数S(x)∈C2[a,b],区间[a,b]之间存在着数据节点a=x0 (1) (2) 对该矩阵进行求解得其结果,代入式(1),可以得到每个小区间的三次样条插值函数表达式。 考虑到三次样条插值计算量较大,为此在本文中,利用软件Matlab工具箱的spline函数[11]完成上述计算。具体代码如下。 4)插值估算所求时间的对应沉降量:m′=spline(t,p,t′)。 通过上述过程,原始沉降数据就转化成为了等时距沉降数据,为下一步非等时距灰色预测模型的建立提供应用基础。 在灰色系统理论中,灰色模型[12-14]建模算法简单,预测精度高,但观测时间不是等间隔的。本文所建立的非等时距灰色模型突破了传统灰色模型应用的障碍,是应用相对简便而且充分挖掘有价值信息的建模方法,其应用性有巨大潜力。 1)设非等时距灰色预测模型的原始序列为X0: X0={x0(1),x0(2),…,x0(n)} (3) 2)对非等时距灰色预测模型原始数列进行累加,可以得到新的数列X(1): X(1)={x(1)(1),x(1)(2),…,x(1)(n)} (4) 3)X(1)的紧邻均值生成序列Z(1); Z(1)={z(1)(1),z(1)(2),…,z(1)(n)} (5) 式中:Z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1) (6) 其时间响应式为: (7) 4)采用最小二乘的理论方法计算得到灰度参数值,参数a,b可以通过建立微分方程求解: (8) (9) 5)计算可以求取参数a,b然后代入(7)即可得到非等时距灰色预测模型。 6)将非等时距灰色预测模型计算新生成的数列累减还原,得到模型的拟合值或预测值。 (10) 式中:k为时间序列,k=2,3…n。 以上非等时距灰色模型建立过程。 非等时距灰色模型精度评定具体标准如表1所示。 表1 模型精度评定标准 预测模型的精度大小是由均方差比C和小误差概率P决定,其计算公式为: (11) (12) (13) 根据以上内容分析,对于本文的非等时距灰色模型算法流程进行简要总结:首先将建筑物原始沉降数据利用Matlab工具箱完成三次样条插值,得到基于原始数据的等时距序列,其次进行非等时距灰色预测模型的建立,得到预测沉降数据。然后进行预测值与实测值的沉降量精度对比,计算平均相对误差、小误差概率、均方差比值,具体流程如图1所示。 图1 沉降预测计算流程 为分析非等时距灰色预测模型应用于建筑物沉降预测的精度效果,根据聊城昌润祥荷园8号楼J81实测数据,利用Matlab代码编程进行三次样条插值法处理,随后进行非等时距灰色模型的建模,并对预测模型进行精度分析。 昌润祥荷园8号楼高层住宅楼项目位于聊城市东昌路以北、徒骇河以西新征地块。共1栋27层高层住宅楼。建筑物主体沉降观测点使用0.3mm精密水准仪观测,采用闭合线路二等水准测量。沉降点布置如图2所示。 图2 平面沉降点布置 聊城昌润祥和园8号楼J81实测沉降数据如表2所示。 表2 聊城昌润祥荷园8号楼J81实测沉降数据资料 根据上文非等时距灰色预测模型理论可知,表2的沉降观测数据均是非等时距的,而所建立的灰色预测模型是建立在原始数据等时距基础上的,为此必须进行等时距处理,方便进行下一步建模工作。本次采用三次样条插值法处理原始沉降数据J81,采用等时间间隔为30d,J81沉降点沉降数据经过三次样条插值法得到的等时距沉降数据如表3所示。 表3 聊城昌润祥荷园8号楼J81等时距沉降数据 通过三次样条插值法得到等时距沉降量,其中1~20属于内插数值,21属于外推数值。为保证精度要求,下面对插值效果进行定性定量分析,如图3所示。 图3 J81实测曲线与三次样条插值曲线效果 由图3可以看出,三次样条插值法的插值效果是很满意的,究其原因,在于三次样条插值法并不是线性插值,区别于线性插值的隆起不平带来的曲线连续性差,反观三次样条插值法在各段连接之处连续性好而且各节点都是光滑连接,因此从根本上保证了插值所得的等间隔序列更加符合工程实际要求,为建立预测模型打下坚实基础。 X(1)= 计算X(1)的相邻均值序列,记为Z(1)即: Z(1)= 构造矩阵Y与B: 利用式(8)求灰色参数a=0.414 3,b=12.249 5,则计算得到观测点的非等时距灰色预测模型的沉降预测公式为: 模型拟合效果比较,比较前15期的拟合精度,如表4所示。 表4 模型拟合效果比较 由表4可知,沉降实测值与预测值误差范围为-0.560 5~0.785 9,相对误差在3%左右。 从检验模型的3种方法上看,精度评定等级也很好,满足了工程要求。其中平均相对误差越小越好,小误差概率越小越好,其中均方差比为0.075 32(见表5),数值比较小,说明残差比较集中,摆动幅度小,原始数据比较分散,摆动幅度大,所以体现的拟合效果是比较好的。 表5 模型拟合精度比较 模型建立的目的是为更好地进行沉降预测,模型预测结果比较如表6所示。 表6 模型预测结果比较 由表6可知,沉降实测值与预测值误差范围为-0.594 5~0.041 7,相对误差在2%左右。 非等时距灰色预测模型的预测沉降值曲线与实测值曲线对比效果如图4所示。模型预测精度比较如表7所示。 综上所述,结合图4以及表5和表7,可以明显看出拟合结果、预测值与实测值的变化趋势非常接近,误差和平均相对误差都很小,由此可见非等时距灰色预测模型的拟合程度较好,能够很好地反映出建筑物沉降变化规律。 非等时距灰色预测模型的精度是建筑物沉降预测的核心问题,因此通过对整个建模过程的思考来看,时间间隔、累计沉降观测数量这两个关键问题的选取显得至关重要。故本文采用控制变量法,对时间间隔和观测次数两种因素进行了预测模型精度分析,为构建高精度的非等时距灰色预测模型提供借鉴。 本文中选取不同时间间隔为T=30,T=60,T=120,控制相同的观测次数为20,进行预测模型的预测值与实测值精度分析。 通过实测插值沉降量和非等时距灰色建模理论由此可以分别得到T=30,T=60,T=120的非等时距灰色预测模型表达式: (k=2,3,…,n) (14) (k=2,3,…,n) (15) (k=2,3,…,n) (16) 由非等时距灰色预测模型表达式可计算各时段的沉降预测值,得到各观测点的沉降预测曲线,从而与实际沉降观测数据进行比较,如表8所示。 进一步计算T30,T60,T120的平均相对误差分别为:1.35%,2.39%,2.04%。 为进一步观察出预测模型的精度,绘制实测曲线与相同观测次数下不同等间隔T30,T60,T120的曲线对比效果如图5所示。 通过表8与图5,可以很明显看出等时间间隔为30d的预测模型精度更优,更加贴近实测曲线,结果表明不同时间间隔,控制不同的沉降观测次数所建立的模型,表明短时间间隔的预测模型精度更好。 图5 实测曲线与相同观测次数下不同等间隔的曲线对比效果 表8 不同等时间间隔下相同观测次数的误差统计 其次控制相同的时间间隔为T30,不同的观测次数。选用10组、15组以及20组建立预测模型进行精度分析,如表9所示。 表9 不同观测次数下相同等时间间隔的误差统计 通过计算可以得到10组、15组以及20组所建预测模型的平均相对误差分别为:2.93%,2.92%,1.32%。 为更清晰观察其预测效果,绘制实测曲线与相同时间间隔T30下不同观测次数10组、15组、20组的曲线对比效果,如图6所示。 图6 实测曲线与相同时间间隔T30下不同观测次数曲线对比效果 通过对比,可以发现20组所建立的灰色预测模型预测精度是更优的。结果表明:相同的时间间隔,不同的沉降观测次数所建预测模型,长时间观测次数的预测模型精度更优。 1)通过本文所建立的非等时距灰色模型,对建筑物沉降进行预测,其拟合效果是满足要求的,精度水平也达到了一级,从而验证了本文非等时距灰色模型在建筑物沉降预测中的可行性,也为其他类似工程预测提供了参考。 2)三次样条插值法处理建筑物实测数据,尤其是在非等时距序列方面体现出优越的拟合效果,其主要因为是良好收敛性、稳定性优越以及二阶光滑度即二阶导数连续等特点,可以在工程数据处理中起到重要作用,为其他类似工程数据处理提供借鉴。 3)本文所建立的非等时距灰色预测模型设置了两个控制因素(时间间隔和观测数据量),当这两个控制因素取值不同时,模型预测结果的精度也不同。选择短时间间隔且长时间观测次数的预测模型精度上会得到更好的预测效果,增加了预测模型的可调节性和优化可能性。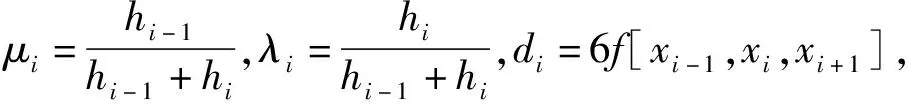
1.2 非等时距灰色模型的建立
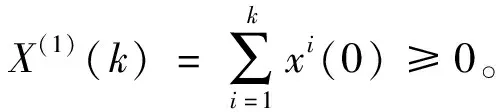
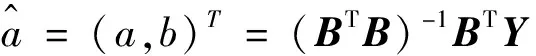
1.3 非等时距灰色模型的精度检验
1.4 非等时距灰色模型的算法流程
2 工程应用实例
2.1 项目概况
2.2 沉降监测数据处理
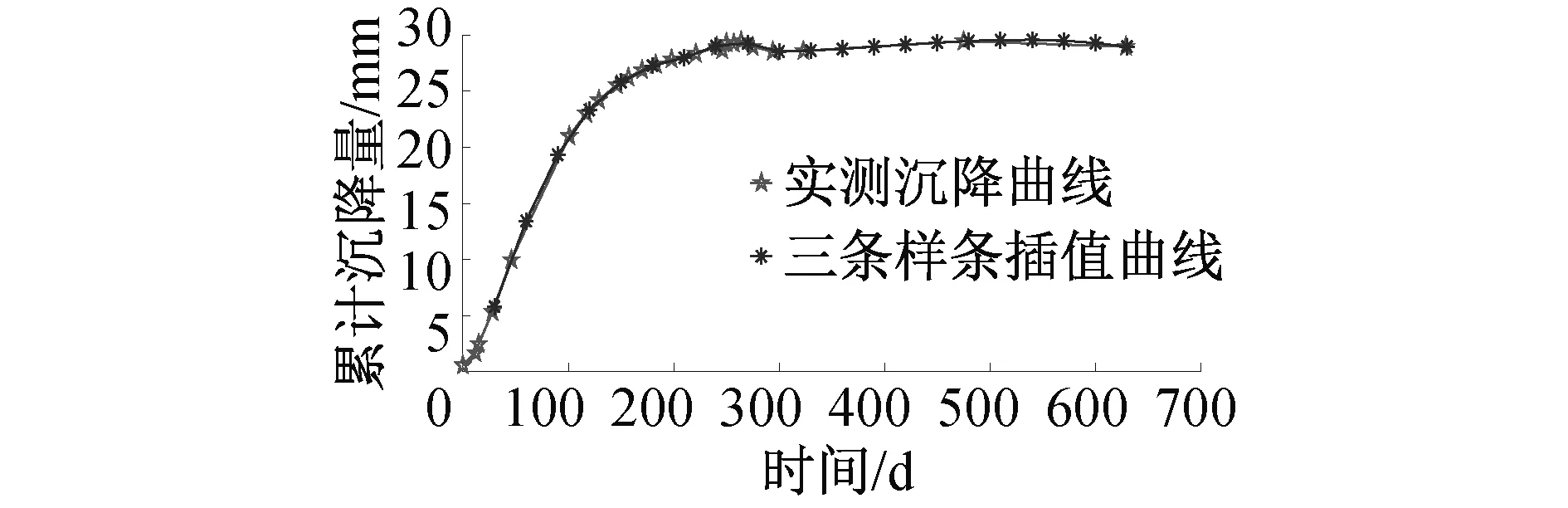
2.3 非等时距灰色模型建立
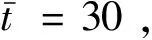
2.4 非等时距灰色模型精度分析
3 影响非等时距灰色模型精度的关键问题
3.1 不同等时间间隔下相同观测次数的精度分析
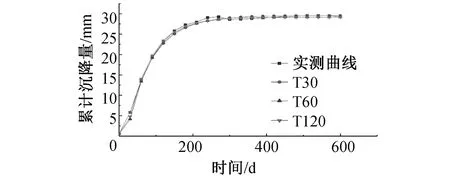
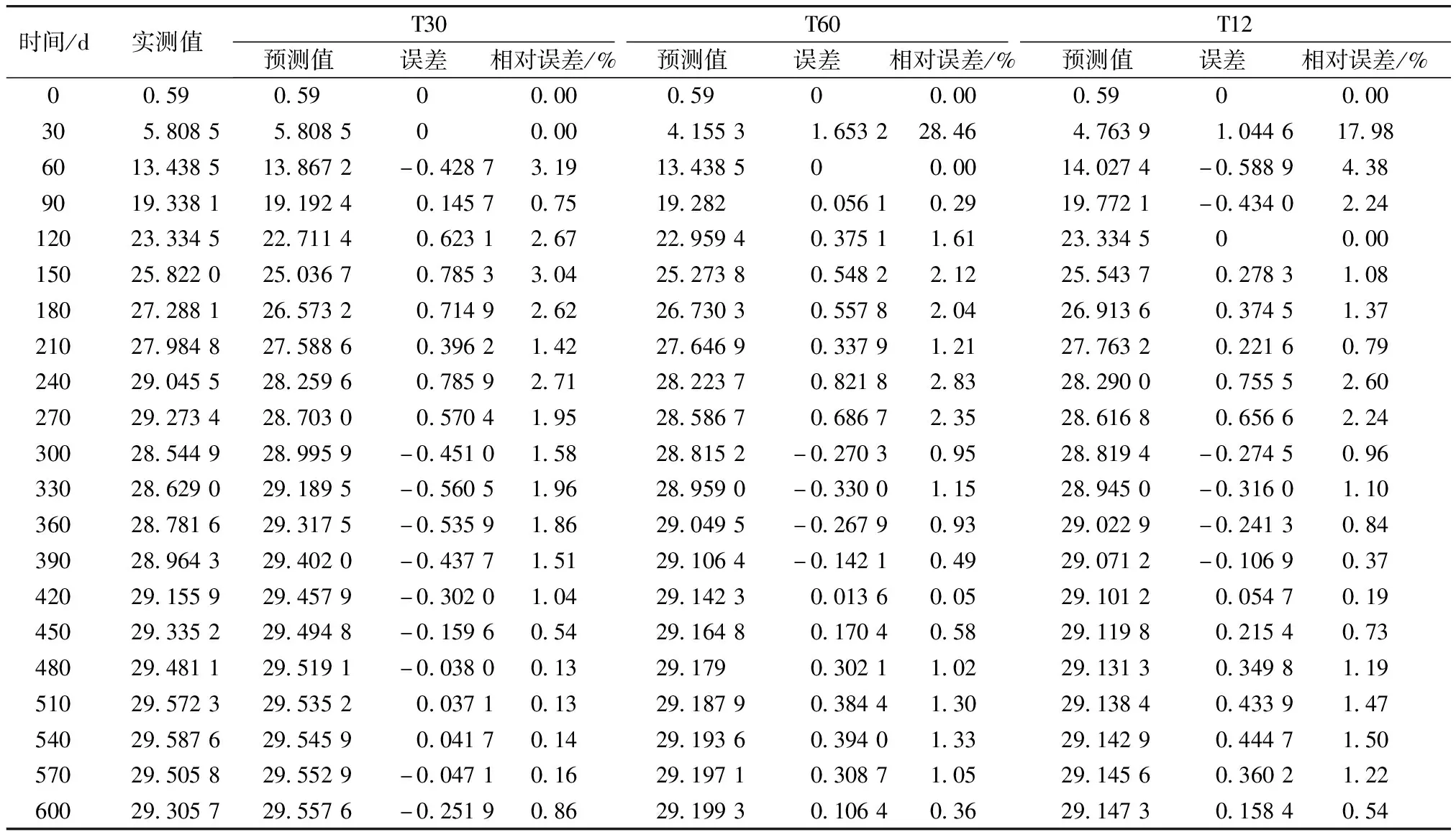
3.2 不同观测次数下相同等时间间隔的精度分析
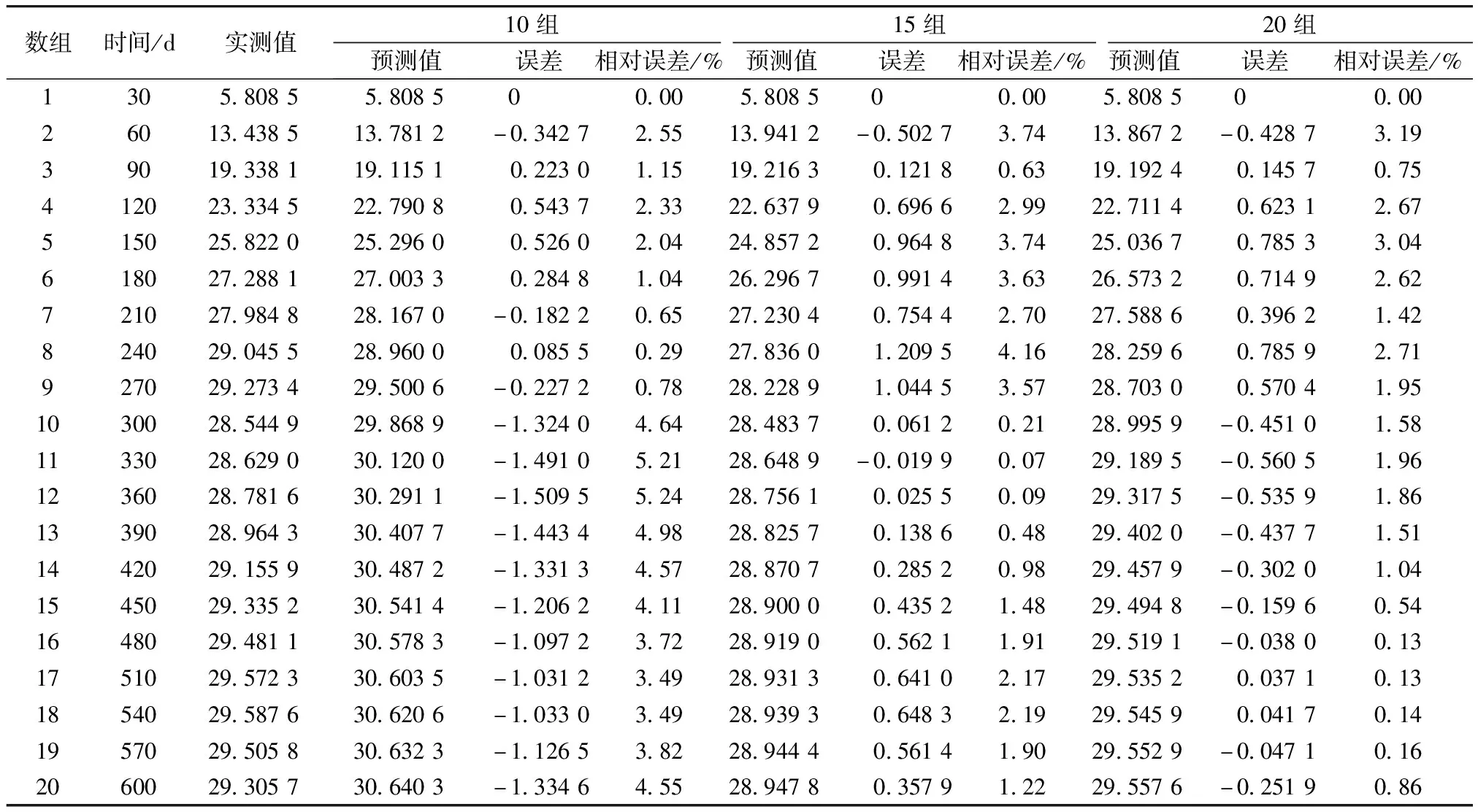
4 结语

