边坡蠕滑影响下桥梁桩基力学特性分析*

王海恩

(洛阳腾飞市政工程有限公司，河南 洛阳 471935)

0 引言

随着现代交通对道路工程线型和平顺性要求的提高，边坡上修建高架桥梁的情况越来越常见，该类桥梁在承受车辆动荷载的同时，又受到边坡侧向力和雨水等因素的影响，当坡体发生变形时，桥梁桩基不可避免会被推挤，造成桩基甚至桥梁的破坏。郑明新等[1]通过映射分析认为降雨是铁路运营期间影响滑坡发育的最活跃因素，降雨导致的滑坡同时也会带动边坡桥梁变形，主要为土体推动桩基所致。目前国内外学者对于边坡桩的探索主要集中于抗滑桩的力学性能研究[2-3]。邓会元[4]依托台州湾大桥对不平衡堆载条件下在建桩基的力学特性进行了试验研究；赵明华等[5-6]依据现场试验方法提出了倾斜荷载作用下单桩的有限差分计算方法，并根据陡坡段桥梁桩基承载力特性对该方法进行了进一步改进；蔺鹏臻等[7-8]对考虑边坡效应的桥梁桩基力学性能进行了分析，并对比了恒荷载和考虑组合荷载工况下桥台和桥墩承台中心桩基的力学响应。目前针对桥梁桩基的研究主要集中在其竖向受力方面，对边坡蠕滑作用下不同位置的桥梁墩台及同一墩台不同位置桩基的力学特性尚缺乏深入研究。本文以某发生病害的桥梁为依托，基于有限元软件平台，建立了考虑土体非饱和特性的边坡降雨分析模型，并考虑桩土之间的滑移，研究了桩基在车辆荷载和降雨作用下的力学规律，获得了较为精确的桩基力学响应规律。

1 工程背景

某桥梁为8×32m+2×24m简支梁桥，其中0～4号桥墩处于近500m长边坡上，坡度近45°；坡底距钢轨顶面41.77m，坡度近40°。桥墩、承台和桩基采用C35混凝土，其中0～3号桥墩采用圆端形实体桥墩，桩基按摩擦桩设计；4号墩采用圆端形空心桥墩，桩基按柱桩设计，桩底嵌入云母石英片岩内。桩基础设计如表1所示。

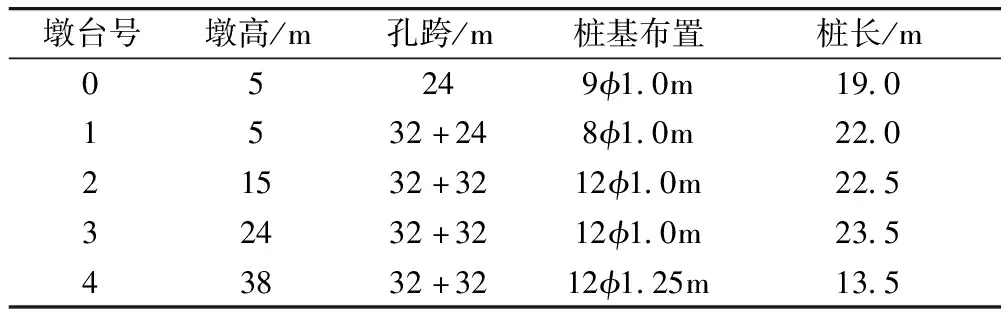
表1 桥梁桩基础设计情况

桥址区岩土层由上至下为：①粉质黏土 硬塑，σ=180kPa；②云母石英片岩 全风化，σ=250kPa；③云母石英片岩 强风化，σ=400kPa；④云母石英片岩 弱风化，σ=800kPa。地下水为孔隙潜水及基岩裂隙水，坡底处地下水位距地面4m，坡顶处水位距坡顶35m。桥梁基础立面如图1所示。

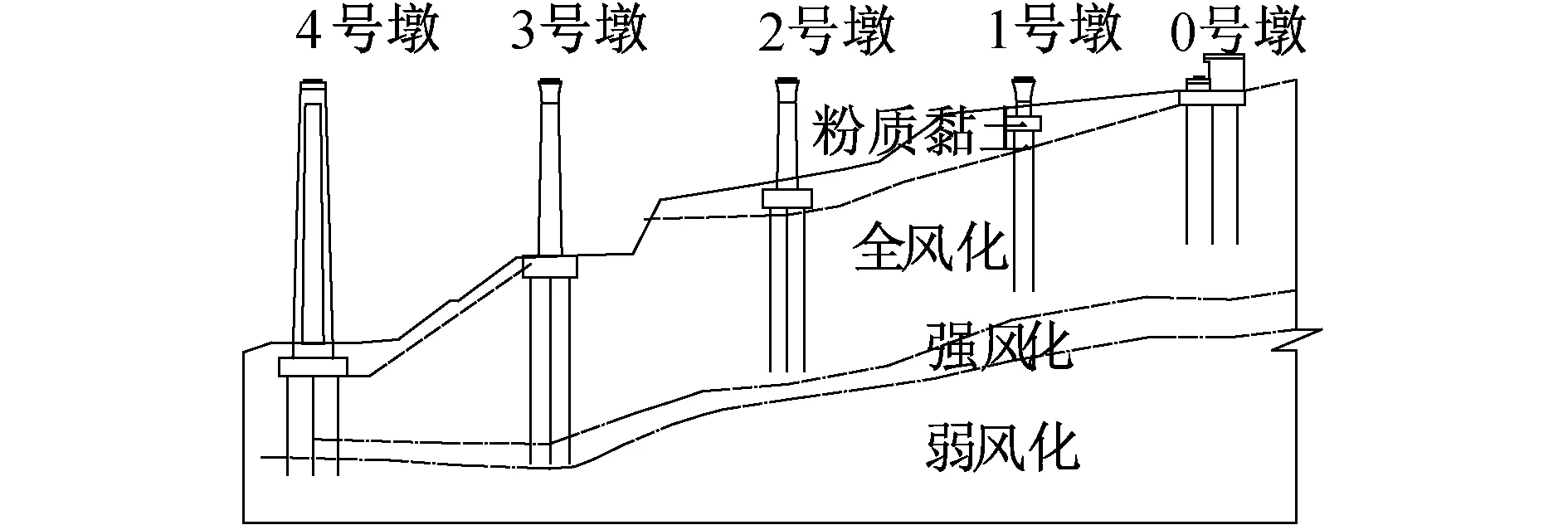
图1 桥梁基础立面

桥梁0号墩外接20m过渡段路基及其后的双线隧道。通车1年后检查发现，1号墩支承垫石砂浆垫层局部脱落。从桥梁监测数据、桥上裂缝、支座滑移、土体裂缝分析，均表明0～4号桥梁墩台向低山侧发生了偏移。与通车时相比，位于山坡上的1～4号墩顶坐标均有变化，其中4号墩顶沿纵向向坡外偏移13.4mm，3号墩顶偏移21mm，2号墩顶偏移34.4mm，1号墩偏移44.3mm，0号台偏移21.8mm；4号墩沉降0.4mm，3号墩沉降7.5mm，2号墩沉降14.8mm。

2 数值分析

为探究边坡桥梁在边坡变形阶段的力学规律和安全性，以该边坡桥梁工程为依托，建立三维边坡模型。

2.1 有限元模型

为保证模型能够包括边坡的危险面，并避免边界对模型计算精度产生影响，本工程模型尺寸选取为：坡前模型高53.6m，坡后高193m，坡长478m，横向50m。边坡土体、桥墩、桥梁和承台采用实体单元，桩基采用梁单元。土体采用修正莫尔-库伦本构模型，可同时考虑土体的剪切硬化和压缩硬化，混凝土采用弹性本构模型。水力边界为：坡体后侧158m高采用固定水头边界，35m采用溢出边界；前侧50m设置固定水头边界，河道处采用溢出边界，边坡表面设置面流量模拟降雨。位移边界为：前、后、左、右侧约束法向位移，底部约束3个方向位移；桩基设置旋转约束。

0～3号墩台桩基建立桩界面单元，4号墩桩端设置桩端单元，以模拟梁单元和地基之间的摩擦行为和相对位移；其中0～3号墩台桩基为摩擦桩，依据勘察报告和规范取桩周摩擦力设计值如下：云母石英片岩、全风化层取f=80kPa，云母石英片岩、强风化层取f=120kPa。4号墩端承桩桩底位于全风化云母石英片岩层，桩底压缩模量为30MPa。

综合地勘报告、现场试验结果和GB50218—2014《工程岩体分级标准》[9]确定土层参数如表2所示，桥台、桥墩、承台和桩基参数依据规范取值。

表2 材料参数

2.2 降雨计算

文献[10]的研究结果表明，由于土体渗透能力的限制，当降雨强度超过土体的渗透能力时，降雨并不能被土体吸收，连续小强度降雨对边坡的稳定性影响更大。采用面流量模拟降雨，计算时若地表吸水能力小于降雨量，可以认为地表面土体处于饱和状态，等同于水位存在于地表面上，此时将降雨饱和区变更为水位线。

计算按照最不利工况，依据当地统计最大降雨强度300mm/d，将7天的降雨量作为总量，分28d施加在模型上。计算中非饱和特性函数渗透性函数依据参数取加德纳系数a=0.1，n=2，含水率函数依据参数取θr=0.3，θs=0.6，a=0.1，n=2，m=0.5。

3 计算结果分析

3.1 滑裂面位置分析

计算结束时边坡出现滑移的滑裂面如图2所示，1～3号墩桩基穿过滑裂面，滑裂面距离1号墩处地表面为18.5m，距离2号墩处地表面为23m，距离3号墩处地表面为16.2m。0号墩处土体并未出现滑动，墩顶位移系上部桥梁牵拉倾斜(导致1号墩顶垫石崩裂)，4号墩亦位于滑裂区域外，其墩顶变形由3号墩桥梁顶推所致。

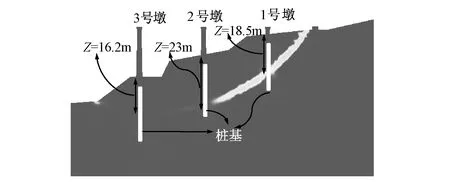
图2 滑动面和桩基相对位置

3.2 桩基位移分析

1～3号墩台桩基均位于滑坡周界内，将每个承台远离坡顶方向一侧的桩基命名为 “前排桩基”，向坡顶命名为“中间桩基”“后排桩基”；远离坡顶方向位移为负，相对一侧为正。

各桩基的位移情况如图3所示，桩基的最大位移为-42.3mm，出现在1号墩台的后排边桩上，受桩顶承台和上部桥梁的约束，最大值出现在距离桩顶4.5m处。取各墩下位移最大的桩基进行分析，如图3a所示，位于坡后的桩基位移大于坡前桩基，其中1号墩桩基底部出现了正向位移，桩基在滑动土体的带动下出现了向坡前方的倾倒，倾倒的旋转轴位于滑裂面处；桩顶处受到承台和上部桥梁的约束，桩基位移有所减小。2号墩桩基的最大位移出现在桩顶处，桩基位移在滑动面附近的变化速度较快，沿滑动面向上基本为一竖直线，其位移大小沿深度变化不大。3号桩基位移相对较小，桩基的变形趋势为整体向坡前倾斜。

图3 桩基水平位移随深度变化

图3b～3d为各墩台下不同部位的桩基位移随深度变化情况，由图可知，由于承台的约束作用，每个墩下桩基桩顶位移相同，各墩后排桩基的位移值整体较前排大。桥梁的存在对桩基变形产生了约束作用，侧移值越大，约束作用越明显，1号墩台顶端甚至出现了位移越靠近地表越小的情况。

3.3 桩基内力分析

1～3号墩台桩基桩间距均为2.7m，分别取各墩的前、中、后3排桩基横向的外侧、中间桩进行分析。1～3号墩桩基的弯矩分布如图4～7所示。由图4可知，桩基最大弯矩值为1 120.3kN·m，出现在1号墩距离桩顶9.9m处的后排边桩上，反弯点位于滑裂面处。边桩的最大弯矩大于同排内桩的最大弯矩，1号墩台后排边桩和内桩的最大弯矩差值为164kN·m，占后排内桩最大弯矩值的17%；前排边桩和内桩的最大弯矩差值为247.15kN·m，占前排内桩最大弯矩值的28%。

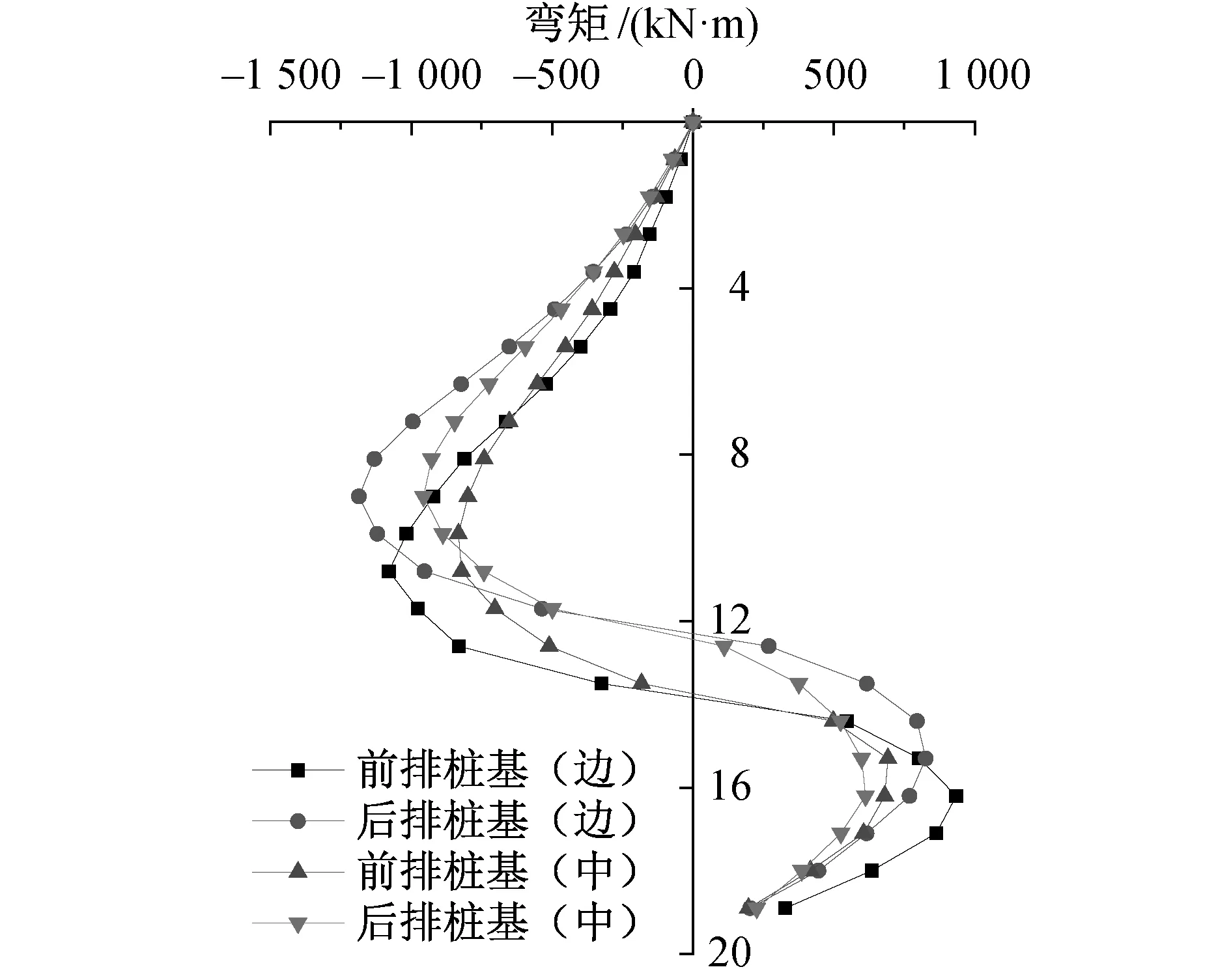
图4 1号墩不同位置桩基弯矩随深度的分布

如图5所示，2号墩台桩基最大弯矩值出现在距离桩顶部17.5m处的后排边桩上，为579 kN·m。后排和中排桩基坡整体受拉，前排桩基桩顶部分则表现为受拉。其边桩的最大弯矩大于同排内桩的最大弯矩，后排边桩和内桩的最大弯矩差值为378.9kN·m，占后排内桩最大弯矩值的18.8%；前排边桩和内桩的最大弯矩差值为54.6kN·m，占前排内桩最大弯矩值的26.8%；中间1排桩基边桩和内桩的最大弯矩差值为80.6kN·m，占内桩最大弯矩值的27.3%。

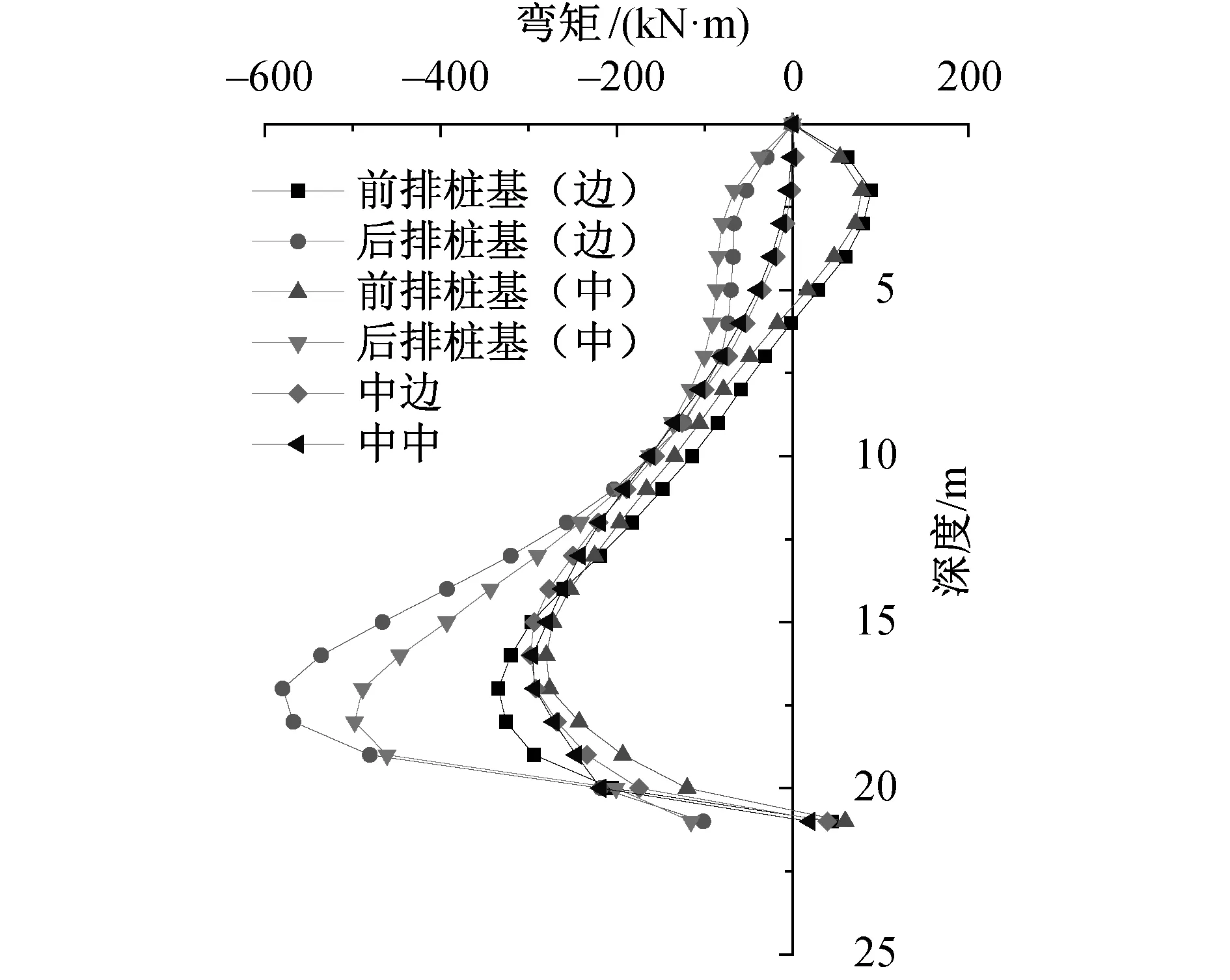
图5 2号墩不同位置桩基弯矩随深度分布

如图6所示，3号墩台桩基整体弯矩较小，前、中、后3排桩的弯矩分布规律和2号桩较为相似，其最大弯矩值靠近桩顶，后排桩基整体受拉，前排桩基桩顶附近受拉。

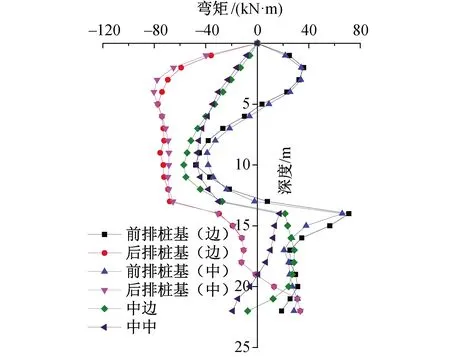
图6 3号墩不同位置桩基弯矩随深度的分布

将每排桩基中边桩、内桩的弯矩极值差值除以桩间距，发现后排桩基中边桩和内桩弯矩极值差值约为内桩弯矩极值的6.7%S(S为桩间距)，前排桩基中边桩和内桩弯矩极值差值约为内桩弯矩极值的10%S。

将1～3号墩最大弯矩的桩基弯矩分布进行对比分析如图7所示，位于坡顶处的1号墩桩基上部坡前侧受拉作用明显，下部坡后侧受拉作用明显；2号墩桩基则表现为下部坡前侧受拉。各桩基的弯矩极值位置和滑裂面位置关联性较大，均出现在滑裂面附近处。

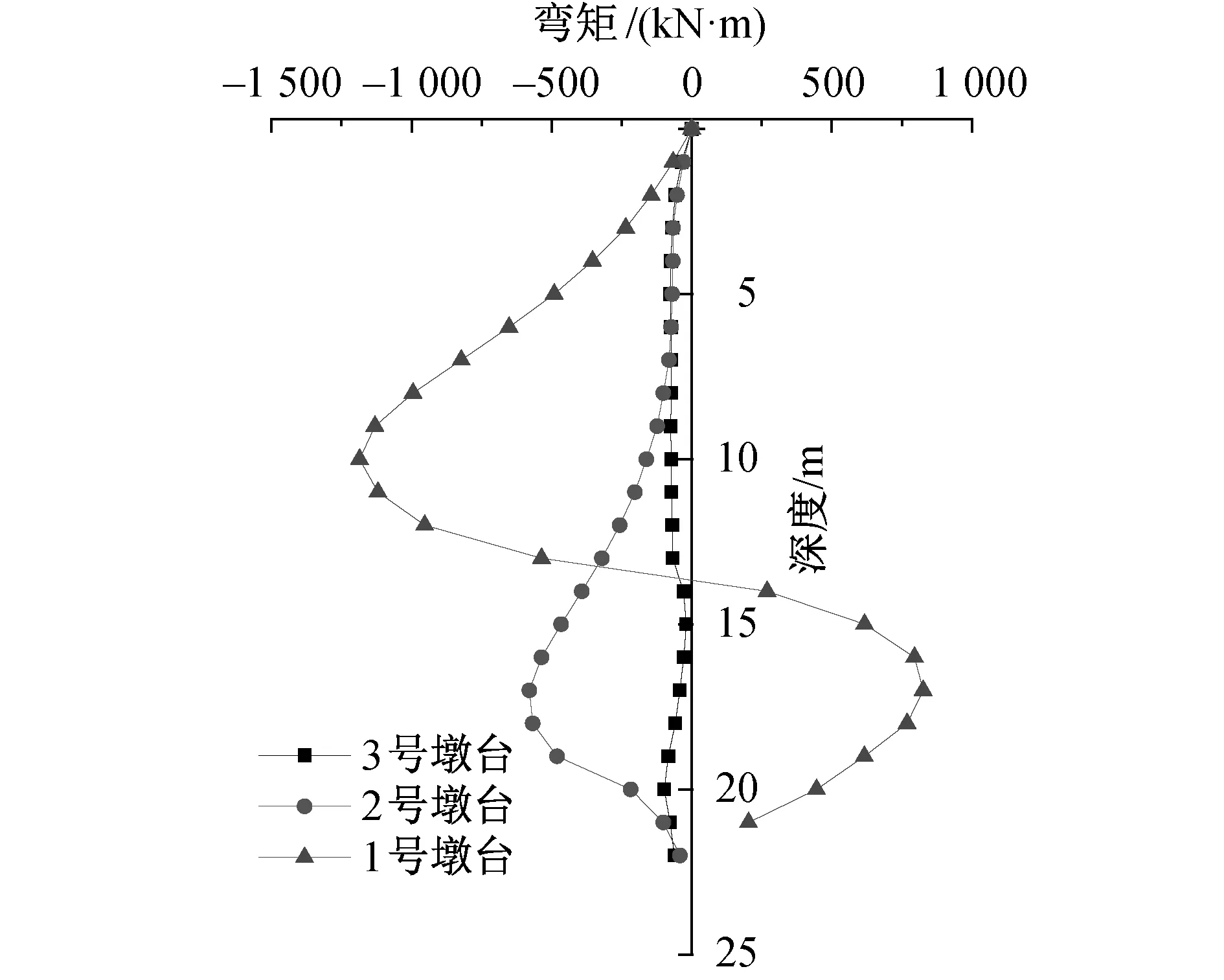
图7 1～3号墩后排桩基弯矩随深度的分布

4 结语

本文以某蠕滑边坡上发生病害的桥梁为例，通过对某边坡上的桥梁不同位置的墩台桩基的计算分析，可以得出如下结论。

1)在边坡发生滑移后，桩基发生整体向坡前方向的倾斜，各墩下后排桩基的位移值整体较前排大。

2)同一桥墩下的各桩基：后排桩基弯矩极值大于前排桩基弯矩极值，同一排桩基中边桩的弯矩极值大于内部桩基弯矩极值；后排桩基中边桩和内桩弯矩极值差值约为内桩弯矩极值的6.7%S，中、前排桩基中边桩和内桩弯矩极值差值约为内桩弯矩极值的10%S。

3)同一墩台下不同位置桩基在受到滑坡推力作用后会产生较大的内力差，在进行边坡桥梁设计时，不仅要考虑坡体的推力，还应考虑同一墩台不同桩基的差异配筋。