基坑围护墙体变形多因素影响研究*

刘文俊，傅鹤林，李小海，王 翔

(1.怀化学院基建处，湖南 怀化 418000；2.中南大学土木工程学院，湖南 长沙 410075)

0 引言

随着我国城市化进程的推进，城市土地资源变得更加宝贵，为了增加土地利用率，地下空间的开发利用成为热点，基坑的合理设计和安全施工显得尤为重要。研究基坑围护墙体变形的影响因素及其影响规律则首当其冲，目前研究方法主要有弹性地基梁m法、杆系有限元法、数值模拟法等。周绍源[1]等以成都某建筑场地深基坑设计为例，采用弹性地基梁m法进行基坑支护设计，利用幂级数求解墙体位移。张强勇[2]根据弹性地基梁弹性杆系有限元法，对深圳市民广场深大基坑桩锚支护结构进行了设计计算，获得了支护桩桩身位移随开挖过程的分布变化规律。李涛等[3]基于桩结构分段分坐标法和弹性地基梁法，推导出了考虑桩-土-内支撑共同作用的支护桩体挠曲微分方程，计算获得了不同开挖深度的桩体水平位移。陈震等[4]以山东省会文化艺术中心深基坑工程为背景，通过理论计算和数值模拟对桩体在不同插入比下的稳定性进行分析。段绍伟等[5]利用非线性有限元方法，研究了基坑深度、墙体长度及墙体插入深度对深基坑开挖变形的影响，具体研究了墙体侧向挠度、地表沉降和坑底隆起的变化。在这些研究中，没有求解出墙体位移与各影响因素的具体关系(即数学表达式)，同时没有给出经济合理的插入比与围护墙体厚度。

本文基于弹性地基梁张有龄法，求解出墙体位移的解析解，进而通过算例分析墙体位移与插入比、墙体厚度之间的变化规律，得出经济合理的插入比与围护墙体厚度，结合FLAC3D模拟工况与其理论规律对比分析，并运用于实际工程中验证其可靠性。

1 墙体扰曲微分方程构建

建立Winkler弹性地基梁计算模型[6]，该模型将桩墙支挡结构视作支撑在弹性支座上的梁，基坑外侧作用已知的土压力，即开挖面以上土压力按朗金土压力理论计算，在开挖面以下假定为矩形分布，基坑内侧土体h2对桩墙支挡结构的地基反力用一系列土弹簧模拟，桩墙底部简化成滚轴支座，如图1所示。

图1 弹性地基梁法计算简图

本文采用张有龄法[7]，假定地基水平基床系数k沿深度为常数，这对于超固结黏性土与表层压实的砂土比较适合。桩墙在侧向土压力和土的弹性抗力共同作用下，桩墙的挠曲微分方程按弹性地基梁张有龄法计算，对于开挖面以上的桩墙，k=0，故其挠曲微分方程为：

(1)

式中：E为桩墙的弹性模量；I为桩墙的截面惯性矩；y为桩墙的挠度；r为土的重度；z为墙体深度；ka为主动土压力系数；k为地基水平基床系数；b为墙体厚度；h1为开挖深度。

2 扰曲微分方程求解

对式(1)中0≤z≤h1区间进行积分处理，求得式(2)，式(1)中h1≤z≤h1+h2区间根据弹性地基梁的计算方法[8]，可以求得式(3)。

(2)

(h1≤z≤h1+h2)

(3)

(4)

(5)

式中：φ1′，φ2′，φ3′，φ4′的值为φ1，φ2，φ3，φ4在x=h2时求得的值。

(6)

(7)

将式(4)～(7)带入式(2)～(3)中，即求得扰曲微分方程的解析解，根据墙体侧向位移y的关系式，很明显可以看出y与开挖深度h1、土弹簧深度h2、墙体厚度b有关。

3 理论算例分析

3.1 最佳插入比的确定

假定某工程中，E=25×106kPa，I=8×10-3m4，r=20kN/m3，墙体总深度h1+h2=12m，ka=tan2(45°-φ/2)=0.5，k=4×104kN/m3。根据墙体侧向位移y的关系式，求得当b=1m时，墙体侧向位移随开挖深度变化曲线如图2所示。

图2 当b=1m时，墙体侧向位移随开挖深度变化曲线

从图2可以看出，基坑土体开挖后，侧向卸载导致坑外土体向基坑内移动，引起围护结构发生侧向位移，随着基坑开挖深度h1的增加，墙体侧向位移不管是正向还是负向都在增加，而且增加的幅度越来越大；墙体转动中心则随着开挖深度的增加均匀向下发展，墙体转动中心位置均在开挖面以下2m处发生；墙顶水平位移突出，变化最大，对墙体稳定性影响最大。

为研究墙顶水平位移和h1，h2之间的变化规律，本文引入桩体插入比λ，是指基坑支护工程中，竖向围护结构在基坑底面以下长度与基坑底面以上长度之比，即h2/h1，随着开挖深度h1的变化，自然形成不同的插入比，画出墙顶水平位移在不同插入比时的变化情况如图3所示。

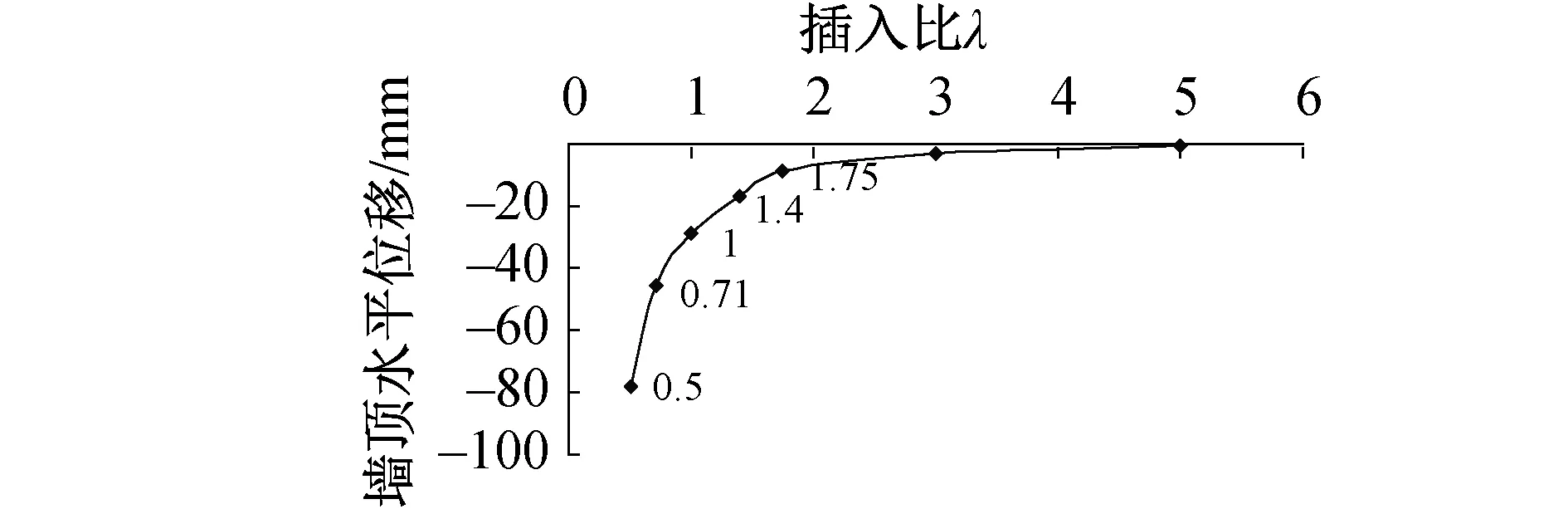
图3 不同插入比对墙顶水平位移的影响

从图3可以看出，墙顶水平位移随着插入比的增加先逐渐减小，后趋于稳定，并逐渐向0靠拢；当插入比>1.4时，墙顶位移很小，插入比的增加对减少桩顶水平位移的贡献越来越小；当插入比<1时，墙顶水平位移值较大，增长变化率极大，严重将发生倾覆或翘起。而开挖至插入比为1.0～1.4时，墙顶水平位移值较小，增长变化较平缓，所以此插入比较为经济合理，如继续开挖，插入比减小，则应开始加设横撑、斜撑等支撑结构。分析可知，此插入比只适用于开挖一定深度范围内的基坑，因为开挖深度过大，墙顶水平位移在未达到插入比1.4之前，就超过允许值而失稳，所以在运用此最佳插入比1～1.4时，应根据工程实际情况预先计算墙顶位移值。

3.2 最佳围护墙体厚度的确定

当λ=1时，改变墙体厚度，b分别取值0.5，1，1.5，2，2.5，3m，墙体侧向位移变化情况如图4所示。分别计算λ为1，1.4，1.75情况下，不同墙体厚度b对墙顶水平位移影响情况，如图5所示。

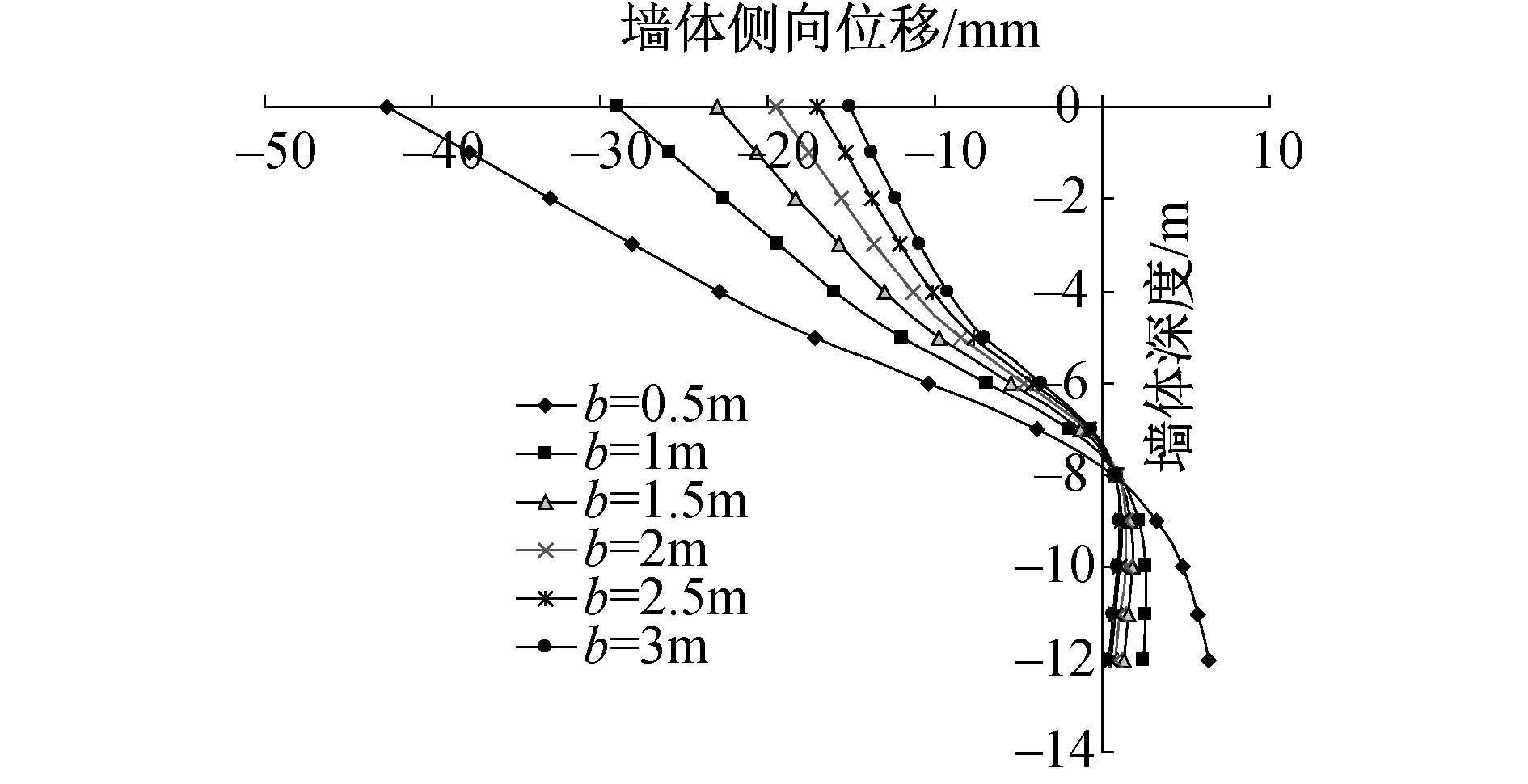
图4 当λ=1时，墙体侧向位移随墙体厚度变化曲线

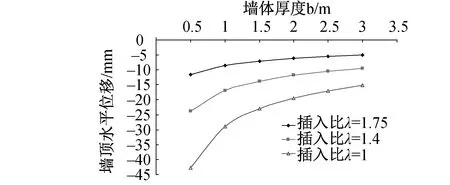
图5 不同的λ值，墙顶水平位移随墙体厚度变化曲线

从图4可以看出，随着墙体厚度的增加，墙体侧向位移逐渐减小，减小幅度逐渐递减；墙体转动中心则保持不变，进一步印证了转动中心为开挖面以下2m处，与墙体厚度无关。

从图5可以看出，插入比越小，桩顶水平位移越大；在不同插入比情况下，改变墙体厚度，桩顶水平位移变化规律相同，先随着墙体厚度的增加而逐渐减小，最后趋于稳定，拐点位于1m处，即墙厚<1m时，墙顶水平位移增长率突然变大，而墙厚>1.5m时，继续增加墙体厚度，对减少墙顶水平位移已无较大作用，所以较为经济合理的墙体厚度为1～1.5m。

4 工程实例

4.1 工程概况

怀化学院西校区棚户区改造(清雅苑一期)2号楼工程，地层自上而下分别为素填土、残积相粉质黏土、强风化页岩、中风化页岩、微风化岩层，层底高程分别为-3.000，-9.000，-13.000，-15.000，-20.000m，无地下水，其中素填土、残积相粉质黏土在长期的次固结作用下，具有超固结土的特性。临近校图书馆施作地下室，需开挖基坑6m，设计院根据地质水文情况，按照规范要求并参考文中确定的插入比与桩墙厚度，设计灌注桩排桩围护墙，桩长12m，桩径1m，轴心间隔2m灌入土中，桩身混凝土强度等级C35，纵向受力钢筋HRB400，直径16mm，箍筋直径10mm。

4.2 建立模型

根据模型的建立原则，本文建立的模型尺寸为：长×宽×高=36m×36m×30m，取二分之一模型如图6所示，土体采用莫尔-库仑理想弹塑性模型模拟，灌注桩排桩围护墙采用实体单元各向同性弹性模型模拟。根据工程地质勘察报告确定模拟计算参数，如表1所示。

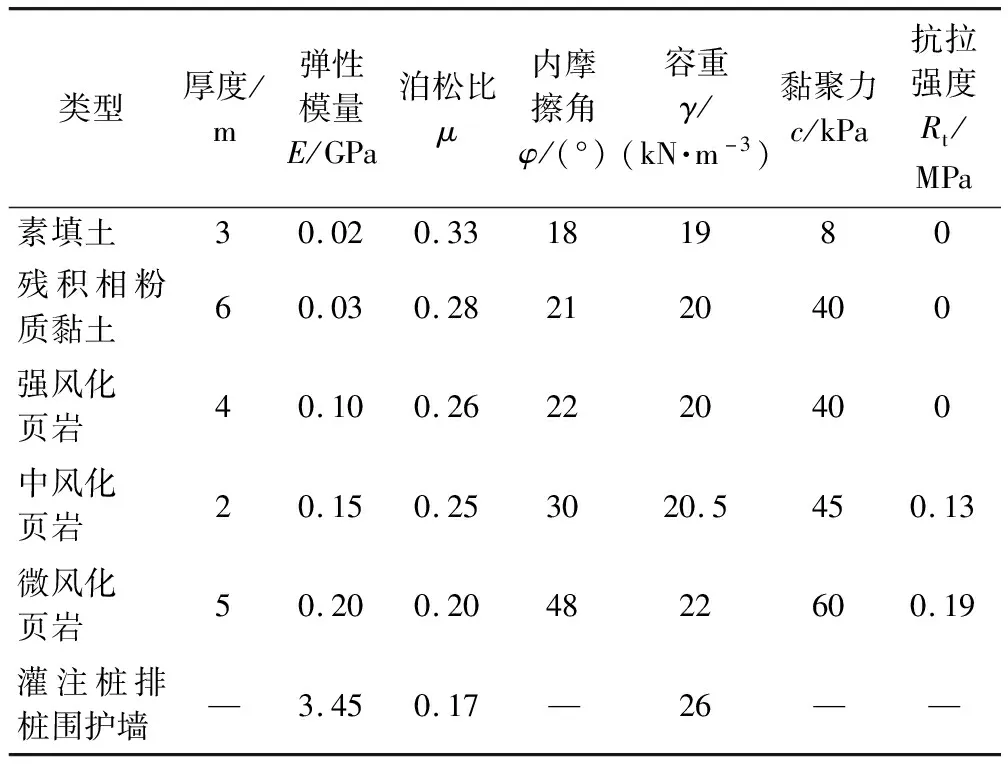
表1 模拟计算参数

图6 三维数值模型

4.3 模拟与理论规律的对比分析

模拟工况1，取灌注桩排桩围护墙厚b=1m时，按照1m的开挖步距，逐级向下开挖至6m处，形成不同插入比情况下的墙顶位移值，提取基坑轴线上墙体位移变化值、墙顶水平位移值，如图7，8所示。

通过图7与图2比较可以看出，土体开挖后，墙体侧向位移模拟规律与理论规律较为相似，侧向位移均随着开挖深度增加而增加，墙顶水平位移最大，但模拟工况由于考虑了坑内土体的上浮现象，而使得墙体发生同向的侧向位移，无明显的转动中心。

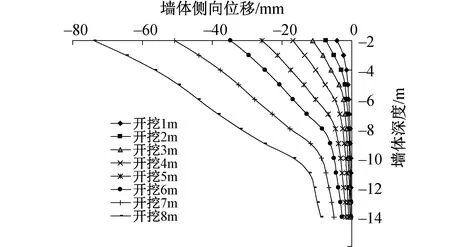
图7 当b=1m时，墙体侧向位移随开挖深度变化曲线

图8与图3比较可以看出，不同插入比对墙顶水平位移的影响模拟规律与理论规律一致，均在插入比为1～1.4时，墙顶水平位移值较小，增长变化较平缓。

图8 不同插入比对墙顶水平位移的影响

模拟工况2，取插入比λ=1时，灌注桩排桩围护墙厚b分别取值0.5，1，1.5，2，2.5，3m，提取基坑轴线上墙体位移变化值、墙顶水平位移值，如图9，10所示。

图9 当λ=1时，墙体侧向位移随墙体厚度变化曲线

图9与图4比较可以看出，改变墙体厚度，墙体侧向位移模拟规律与理论规律相似，均是随着墙体厚度的增加逐渐减小，减少幅度逐渐递减，模拟工况由于坑内土体上浮，无明显转动中心。

图10与图5比较可以看出，墙体厚度对墙顶水平位移值的影响曲线，模拟与理论一致，同样可以得出墙体厚度为1～1.5m较为经济合理的结论。

图10 λ=1时，墙顶水平位移随墙体厚度变化曲线

4.4 现场监测

当基坑开挖至6m时，插入比为1，此时支护工字钢斜撑，桩顶位移得到很好控制，经过3个月的监控量测，桩顶水平位移最后稳定于58mm，满足二级基坑的规范要求，该工程实践结果表明，在一定开挖深度内，选用插入比1～1.4、支护墙体厚度1～1.5m比较经济合理。

5 结语

1)运用弹性地基梁张有龄法，即假定地基水平基床系数不随深度变化，可求得开挖基坑围护墙体扰曲微分方程的解析解。根据求得的解析解，通过算例分析，得出在一定开挖深度内围护墙体插入比为1～1.4比较经济合理，既能保证墙体位移值较小，又能节约材料，墙体水平位移在此后开始骤增，如继续开挖应加设横撑、斜撑等支撑结构，以保证基坑安全。

2)围护墙体厚度应取1～1.5m比较经济合理。在插入比<1时，围护墙体厚度<1m将产生较大墙体位移值，墙体厚度>1.5m时，对减少墙顶水平位移已无较大作用，浪费材料。

3)运用FLAC3D模拟工况与理论规律对比分析，结论一致，应用于实际工程中安全可靠，可为类似工程提供较好的方案支持。