基于区间数聚类的目标分群算法

王海滨, 关 欣, 衣 晓

(海军航空大学, 山东 烟台 264001)

0 引 言

态势认知是指挥控制活动的核心环节,是有效决策和正确行动的前提和基础。目标分群作为态势认知的重要基础,其主要作用是综合考虑目标位置、速度、属性等要素,将各类传感器观测到的目标信息按照一定的规则进行划分,得到相应的分群结果,进而有助于发现目标各类战术意图。

目标分群作为态势认知中的难点和重点,目前比较成熟的研究成果主要有：基于空间数据挖掘技术的目标分群方法、基于模糊集理论的目标分群方法、基于多属性的目标分群方法等。文献[3]根据目标位置和速度信息,采用基于模糊等价关系的方法实现目标分群。文献[4]将目标分群转化为数据集聚类问题,通过计算目标间的流形距离来衡量目标间的相似度。文献[5]利用目标与目标之间的相似度构建目标分群矩阵,通过分群矩阵运算实现对目标分群的判断。文献[6]通过引入核函数和CNM(Clauset-Newman-Moore)算法,给出了目标分群的具体实现。文献[7]通过基于改进空间划分方法,改善了目标分群类别数未知和阈值选取欠缺有效方法的问题。文献[8]采用基于自组织竞争神经网络,以目标运动状态为依据进行自组织聚类。通过分析发现,国内外目标分群算法主要是以目标空间位置作为分群的基本依据,而随着传感器功能的不断丰富,目标属性等信息日益成为重要的信息来源。另外,传感器探测到的目标数据大多都是不确定或不精确的数据。因此,本文着眼目标分群中信息不确定的问题,提出一种基于区间数聚类的目标分群算法,通过利用目标的多维特征信息,对不确定区间数据的聚类分析处理实现态势认知中的目标分群。

1 区间数描述方法

在态势认知过程中,需要对接收到的目标实体数据进行分析,以估计要素之间的关系,进而建立要素之间的结构。由于测量、计算所带来的数据误差,同时由于信息不完全带来的数据缺乏,使得接收到的目标数据往往是一些不确定的数,因此采用区间数来表示这些具有不确定性的目标数据更符合人类的思维方式,相对于实数表示也更贴近实际。

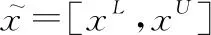
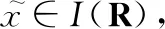
设表示一个非空集合,对于任意,∈,若存在实泛函::×→满足下述条件:

(1) 正定性

(,)≥0,(,)=0,当且仅当=;

(2) 对称性

(,)=(,);

(3) 三角不等式

(,)≤(,)+(,),∈。

则称(,)为两点,之间的度量。

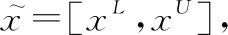
将一般非空集上的度量的定义限制在区间向量空间(),设{}是度量空间((),)中的点列,如果对任意>0,存在>0,使得当,>时,有(,)<,则称{}是()中的Cauchy列;如果()中任何Cauchy列都收敛于()中的点,则称((),)为完备的度量空间。

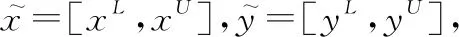
(1)

根据上述给出的区间数距离定义可以看出,两个区间数之间的距离仅仅利用了边缘信息,未能充分利用区间数中心、宽度等信息,因此对于区间数距离度量还存在改进的空间。

2 基于区间数聚类目标分群算法

2.1 问题描述

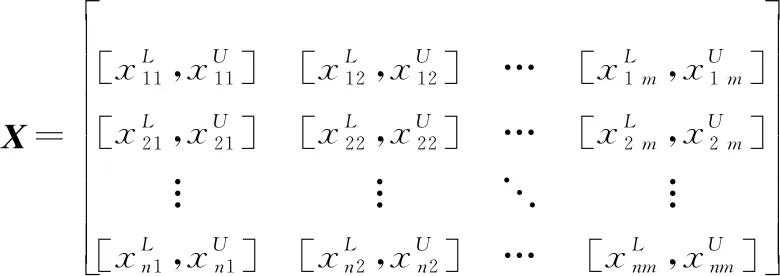
(2)

对于给定的待分类目标,用表示对其进行的划分,一个划分则对应着一个目标分群结果。实质上划分是一个多对一的函数。如果将每个待分类的目标用一个整数∈{1,2,…,}表示,每个分群也用一个整数表示为∈{1,2,…,},那么对于待分类目标的分群就可以描述为=()。所以目标分群聚类的模型可以看成为从目标集到分群,,…,上的泛函。

2.2 区间数及区间向量的距离度量

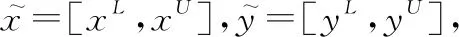
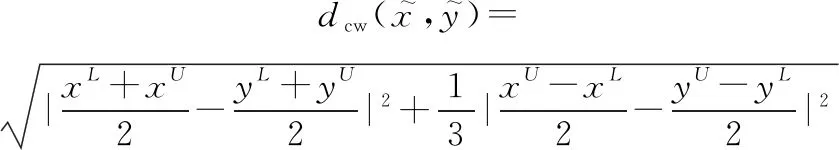
(3)

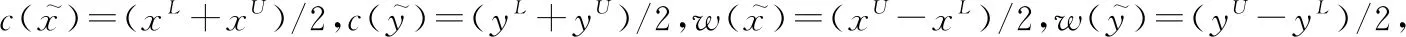
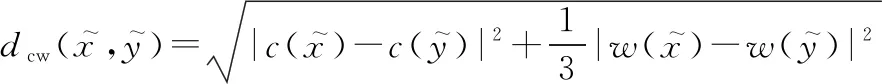
(4)

基于CW的区间数距离不仅考虑了区间数的中点值之差,还考虑了其宽度差,使得区间数的距离刻画更全面和细致。在给出CW度量距离的基础上,进而根据目标区间特征进行目标聚类分析,提出了基于CW度量的区间数K-means(K-means method for interval data using CW metric,IDCWKM)。

(1) 正定性

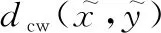
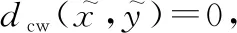
(2) 对称性

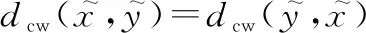
(3) 三角不等式

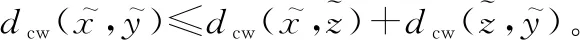
证毕

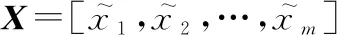
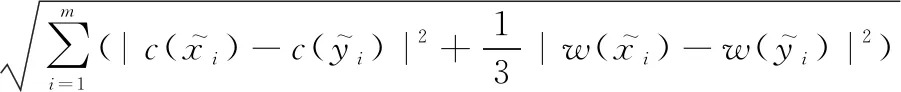
(5)

2.3 IDCWKM目标分群算法

目标分群是将目标按照任务和组织等进行分类,一般是按照类型、运动状态相近或执行相同任务的目标进行分群,以精简态势信息,因此目标分群本质上是一个数据聚类问题。本文在对目标数据进行区间化描述之后,进而定义了新的区间数距离度量。根据区间数聚类模型,可设计不同的聚类算法,聚类算法之间的不同主要体现在目标函数的选择上,但遵循的原则基本上都是最小化群内目标间的距离,同时最大化不同群目标间的距离。与传统的聚类分析目标特征均用实数表示不同,这里研究的是采用区间数据表示的目标特征,而区间目标数据之间的度量是聚类算法的核心问题,因此这里采用前面提出的CW距离作为待分类目标样本之间的距离。

对于聚类有很多实现算法,如K-means就是一种典型聚类算法,K-means聚类的思想是通过损失函数的最小化选取最优的划分。该算法需要事先指定分类数的值,但对于目标分群而言,事先由于缺乏先验知识,并不能给出目标群的值,这给使用者带来诸多不便,并且还可能出现针对同一批目标分群,由于不同使用者理解的不同可能出现不同的分群结果。另外，K-means算法在初始中心选择时呈现随机性特点,导致聚类结果也将出现随机性,进而得不到全局最优解。因此，在目标分群中有必要对K-means算法进行改进和优化。Voronoi图是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成,在数据分析中有重要作用。本文在区间数目标分群中提出了一种基于Voronoi图的改进聚类方法,利用Voronoi图对目标数据空间进行划分。该算法能够依据Voronoi图对聚类初始中心点进行优化选择,避免了K-means算法在初始中心点选择呈现随机性进而导致分群结果不准确的问题。

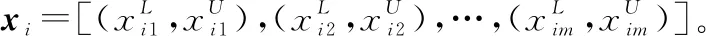
这样对于目标集合分群的关键就是找到一个合理的划分,能够将划分为,,…,和一系列区间均值向量{,,…,},得到最小化聚类误差:

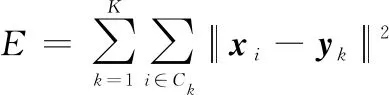
(6)

式中：

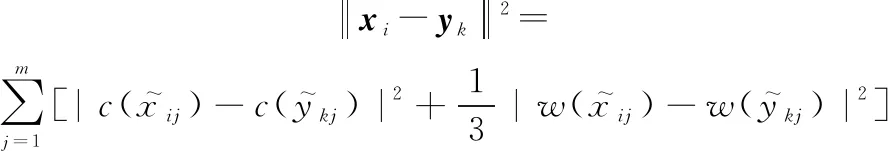
(7)

(8)

目标分群算法是一个迭代的过程,每次迭代包含两个步骤,首先是选择个类的中心,将待分类目标逐个并入与其距离最近的类,这样就得到一个聚类结果;然后更新聚类中心;重新计算每个目标与新的聚类中心的距离,重复以上步骤,直到聚类划分不再改变为止。具体过程如下。

数据标准化

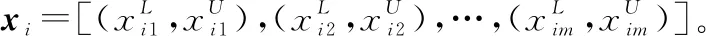
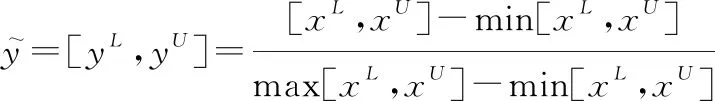
(9)

分配初始聚类中心值

目标集={,,…,}是维的欧氏空间,则的Voronoi图定义为将个目标划分到多个单元中,而每个单元中只含有一个目标,由所决定的区域称为Voronoi单元,用VOR()表示的Voronoi图。用(,)表示空间中目标和的距离,定义隐含了在满足(,)<(,)时一个目标隶属于相应的目标所对应的空间。对于一个Voronoi向量顶点,定义里面不再含有中点的最大空圆为CirU()。

对目标进行聚类划分

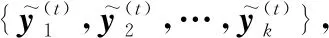
计算并更新聚类中心

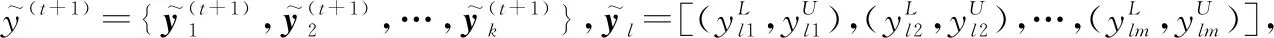
判断循环迭代停止条件

如果迭代收敛或符合停止条件,则停止迭代;否则,令=+1,转步骤3。

2.4 算法评价及分析

为了评价目标分群算法的有效性,可以选取不同的评价指标。评价指标一般有两类,一类是将分群结果与某个参考模型进行比较,称为“外部指标”;另一类是直接考察分群结果而不利用参考模型,称为“内部指标”。为了更为客观评价目标分群算法,这里采用CR(corrected rand)指数,CR指数可以对同一个数据集的不同划分之间的差距进行度量。令={,…,…,}和={,…,…,}分别代表同一目标集合的不同划分,分别包含类和类,则CR指数定义如下:

(10)

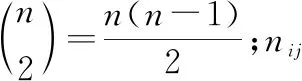
通过分析可以看出,本文算法的时间复杂度主要包括在选取初始中心的Voronoi图算法和自动聚类算法的时间开销。对于选取初始中心的Voronoi图算法,时间复杂度为(log),而对于自动聚类算法,其复杂度为(),其中是目标的特征维数,是目标个数,是类别数,因此本文算法的总复杂度为()。

3 算法仿真

3.1 基于构造区间数据集的算法仿真

在基于构造区间数据集的仿真中,需要在二维实数空间中生成区间数据集。在实验中生成包含4类相互独立的数据集,分别为两类各包含300个数据,一类包含150个数据,一类包含90个数据。生成区间数据集首先需要产生区间数据的中点数据集,而后再根据确定的区间数半径范围生成区间数据的半径,进而构成区间数据集。

假设每一类区间数据的中点由两个服从正态分布的变量所确定,变量的均值和协方差矩阵可表示为

(11)

每一个数据点(,)作为区间数据集的中心点,同时根据设定范围生成的参数和,将其作为在轴与轴上对应中心点数据的半径,即可扩展成一个二维区间数据([-,+],[-,+]),区间数据集半径范围分别为[1,5]、[1,10]、[1,15]、[1,20]。

4类数据集均值和协方差矩阵相关参数分别配置如下。

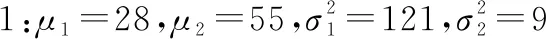
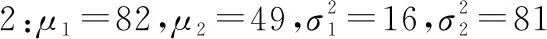
根据上述参数得到的随机区间数据集如图1所示。

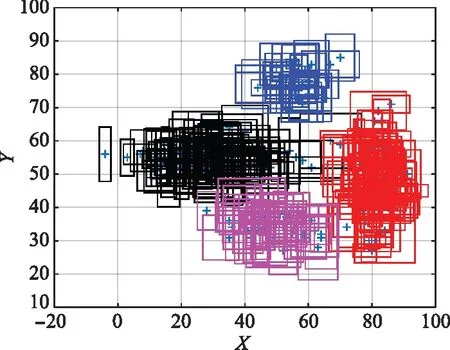
图1 生成的区间数据集Fig.1 Generated interval data set

图2为生成的区间数据集的聚类结果,利用传统的K-means和K-means++算法进行了对比,采用CR指数作为评价指标,本算法得到的CR指数值如表1所示。通过表1的CR值可以看出,利用CW距离作为度量并采用基于Voronoi图的IDCWKM算法相较于K-means和K-means++算法具有更优的聚类效果,能够正确将区间数据集进行分群,CR指数值最高可达0.956 0,即使当区间生成范围为[1,20]时,CR指数值也能达到0.952 2。通过设定不同的区间范围,可以看出基于区间数聚类目标分群算法能够实现对于区间目标数据的有效聚类,证明了算法的准确性。采用传统的Hausdorff距离度量的K-means算法得到的CR指数值仅为0.762 3,可以看出基于CW距离进行目标分群的有效性。

图2 对生成区间数据集的聚类结果Fig.2 Clustering results for generated interval data sets

表1 不同算法目标分群的CR指数表

3.2 目标分群应用举例

为了进一步验证提出的基于区间数聚类目标分群算法的有效性,设计了一个典型场景应用。在此例中,假设共有60个实体目标,编号为T1～T60,目标类型有空中目标和海上目标两种,60个实体目标根据空间属性分为4个空间群,根据任务属性可分为两个任务群。想定目标实体特征包含目标的三维空间坐标(,,)、目标速度、目标航向、雷达截面积、通信频率,且对于想定目标实体特性均由区间数据进行表征,表2给出了部分目标特性数据。目标分群的主要任务首先是对目标实体进行空间分群,在此基础上得到空间分群的聚类中心,进而实现对目标实体的任务分群。

表2 部分想定目标特性区间数据

图3为目标空间分群二维空间显示结果,可以看出空间中不同群目标相互交叠,算法实现了把60个目标实体的空间分群,把60个目标分为4类,分别为空间群S1、S2、S3、S4。图4为目标任务分群三维空间显示结果,可以看出算法能够在空间分群的基础上,进一步实现了对目标的任务分群,分别为任务群A1和A2。为了评价算法的有效性,采用CR指数和准确率作为评价指标,具体数据如表3所示。可以看出利用传统距离度量的目标分群K-means算法CR指数值为0.488 5,准确率仅为74.2%,而本文提出的基于区间数聚类的目标分群IDCWKM算法实现的目标空间分群和任务分群结果与设定相一致,CR指数值为1,准确率为100%。由此可以看出算法对于典型场景目标分群的有效性。

图3 目标空间分群二维空间结果Fig.3 Result of target space grouping in two dimensional space

图4 目标任务分群三维空间结果Fig.4 Result of target task grouping in three dimensional space

表3 目标分群有效性对比

4 结 论

态势认知是指挥控制活动从信息域向认知域跨越的重要标志。本文针对态势认知的关键问题,提出了一种基于区间数聚类的目标分群算法。对于传感器测量数据具有误差、不完全等问题,采用区间数对传感器探测到的目标进行描述。目标分群是态势认知的基础环节,本质上可看作是一个聚类问题,对于聚类问题首先要给出相应的度量,针对目标区间数特征定义了CW度量距离,CW距离能充分利用区间数所包含的信息,在此基础上提出了IDCWKM目标分群算法。为了验证算法的有效性,首先通过构造区间数据集进行目标分群,在二维实数空间生成4类相互独立的数据集。仿真结果表明，所提算法能够对生成的区间数据进行准确分类;其次通过典型想定场景,设定多类目标实体,并根据目标空间位置、运动特征和属性等要素进行空间分群和任务分群,算法能够对多类目标进行准确分群。需要指出的是,由于数据的不完整、不确定以及目标特征的局限性,分群结果会存在一定的误差,对于多种场景下态势要素智能计算及目标分群问题将是下一步的研究重点。