“问题链探究式”生本复习课的教学模式研究
马珂


摘要:新课标倡导自主、自主、合作、探究及反思能力的培养,旨在改变传统的教学方式与学习方式,实现学生学习的主体性地位,培养学生各方面素养的不断发展与提升,以此打破陈旧传统的教学模式。本文以“数形结合思想在二次函数解题中的运用”的教学为例,探究了一种以预习作业和课堂学案相结合的,以典型问题链作为教学平台,以学生自主合作表达、质疑、探究、讨论问题进而努力得到结论为教学主体,以小组合作、生生互动、师生互动为教学形式的“问题链探究式”生本复习课的教学模式。通过在预习作业中设置简单原理性问题,首先引导学生课下讨论自主复习。然后通过课堂练习和预习作业的链式结合,在课堂上引导学生进行深化讨论,在生生合作,师生合作中形成学生的知识体系。问题设置由易到难,由浅入深,环环相扣,尊重学生的认知结构,在逐步深化中不知不觉渗透数学思想。
关键词:生本课堂;学生主体;问题链探究;复习课;数学思想渗透
正文:
复习课是根据学生的复习课足根据学生的认知特点和规律,以帮助学生巩固、梳理已学知识,促进知识的系统化,提高学生运用所学知识解决问题的能力为主要教学任务的一种课型。对于夯实学生基础、培养学生分析问题和解决问题的能力起着举足轻重的作用。
一、问题研究的背景
高中阶段的复习课有一个突出的矛盾,就是在有限的时间里处理繁多的知识点。教师为了增加复习内容,往往表现的主观意识较强,而忽略了学生想怎么复习。传统的数学复习课常常是先由教师带领回顾所学知识,然后学生通过习题来提升对知识的应用能力。复习课常沦为教师主讲的习题课或典型例题分析课,,学生的主体性得不到有效的体现。这样的模式下,学生往往成为做题的机器,缺乏一个自我构建知识体系的机会,也并不能清晰的认识到知识点之间的联系,只不过是跟着教师思路被动的走而已。
新课程的核心理念是以学生发展为本,关注学生全面、和谐的发展,实现学生个性化发展的素质教育理念。新课程倡导学生建构的学习,加强过程性、体验性目标,引导学生主动参与、亲身实践、独立思考、合作探究,以此发挥学生在学习程中的主动性、积极性和创造性,从而实现师生教与学方式的变革,确保每位学生全面、均衡、和谐的发展。
高效的生本课堂,应是一种以学生为中心的课堂。学生主动建构知识体系,而不是在外部刺激下被動的接受和灌输。在教学过程中,教师不应被看作是知识的传授者与灌输者,需要承担起组织、指导、帮助和促进的作用。为此笔者在教学实践中探究了一种“问题链探究式”生本复习课。
二、“问题链探究式”生本复习课的内涵
“问题链探究式”生本复习课通过典型问题链作为教学平台,以学生自主合作表达、质疑、探究、讨论问题进而努力得到结论为教学主体,以小组合作、生生互动、师生互动为教学形式。通过在预习作业中设置典型问题探究,引导学生课下讨论自主复习。然后课堂上通过课堂练习和预习作业的链式结合,在教师的引导下,学生自主分析探究问题,经过深化讨论,在生生合作,师生合作中建构学生的知识体系。问题设置由易到难,由浅入深,环环相扣,尊重学生的认知结构,在逐步深化中渗透数学思想。
同时课堂教学中为了激发学生的主观能动性,促进小组讨论合作机制。教师要引进评价机制,及时对每个小组的表现进行积分奖励。一次积极互动的回答,一个巧妙的解法,一道精心设计的复习题,一个全面到位的总结等,教师都要及时给予肯定和指导,可以给予小组积分奖励。从而提升学生学习的主动性和积极性,并培养学生们的小组合作意识。
三、“问题链探究式”生本复习课的实现步骤
“问题链探究式”生本复习课的教学过程大致分为四个步骤:
(一)课前预习作业的设计
首先教师在课前设置预习作业。预习作业需要教师精心选题,遵循针对性,广泛性,启发、延伸性原则对一节课的关键知识点进行整合。。具体题目的设置要做到低起点,具有针对性和示范性,揭示本节课的概念和原理本质,渗透数学思想,从而使学生可以课前自主探究复习。预习作业题目的设置还应有一定的原则和顺序,环环相扣,层层递进并且和课堂学案遥相呼应,形成一种“问题链”,为课堂探究教学奠定基础。
以笔者在教学实践中“数形结合思想在二次函数解题中的运用”的教学为例,在课前设计了这样一个预习作业:
预习作业1.作出二次函数的图像,并回答:
(1)对称轴方程为: .
(2)顶点坐标为: .
(3)图像和x轴的交点坐标为 .
(4)二次函数的零点是 .
(5)单调递增区间为 ,单调递减区间为 .
预习作业2.求不等式的解集.
预习作业3.求函数的值域.
预习作业4.已知在上是减函数,求实数a的取值范围.
预习作业5.已知方程有两解,求实数k的取值范围.
预习作业6.已知不等式对任意恒成立,求实数k的取值范围.
课前预习作业的设计第1题中二次函数及其图像为着手点,从函数的图像和x轴的交点坐标、顶点坐标、对称轴方程等基础知识入手复习二次函数,是其他题目的基础。预习作业2-6的题目逐步递进,行成“问题链”,学生利用图像逐步递进解决求解一元二次不等式、求二次函数在指定区间上的值域、利用单调性求参数范围、利用图像解决方程的解的个数、一元二次不等式恒成立及在指定区间上恒成立等问题。以题目带知识点,在问题的链式递进中,不知不觉中将数形结合思想渗透在学生的思维能力中。
(二)课前准备阶段
学生们自主复习,完成预习作业,并归纳总结。小组长对预习作业进行批阅,针对每个人的错误,小组内进行生生交流,互帮互助,填补彼此的知识漏洞,从而使每个人形成完整知识体系。在解决小组成员的问题后小组讨论归纳出本节课的复习提纲。小组成员还要针对本组典型错题为本小组讨论设计变式例题。
教师在课前可以对学生的预习作业进行浏览,并收集各小组设计的变式复习题,从而了解学生对本节课的理解情况及知识漏洞,及时对课堂教学的内容和侧重点进行相应的调整。在时间充足的情况下,还可以对每个学习小组设计的变式复习题给予指导和改进意见,让学生深化对重点知识的把握。
(三)教学学案的设计
课前教师需要设计和课堂预习作业配套的课堂学案。课堂学案其实是预习作业中原理与本质知识的深化训练,课堂学案的例题与预习作业中的习题也形成“问题链”。在浏览完学生的预习作业后,结合学生易错点和学生设计的复习题,还可以对课堂学案适当调整。
以笔者在 “数形结合思想在二次函数解题中的运用”的教学实践中的课堂学案设计为例。
(1)探究一:数形结合在解一元二次不等式方面的应用
例1.求函数的定义域
(2)探究二 数形结合在求二次函数值域方面的应用.
例2. 求函数在上的最大值和最小值.
(3)探究三 数形结合在二次函数单调性问题方面的应用
例3.函数在上具有单调性,求实数k的取值范围.
(4)探究四 数形结合在判断方程解的个数方面的应用
例4.已知方程有4个解,求实数k的取值范围
(5)探究五 数形结合在一元二次不等式恒成立问题中的应用
例5.已知函数是R上的奇函数,且在R上递减,若对任意的,不等式恒成立,求实数k的取值范围.
课堂学案的设计上,例1 与预习作业中的第2题遥相呼应,作为预习作业2的深化链式探究,同样例2与预习作业3,例3与预习作业4,例4与预习作业5一一对应。课堂学案的例题正是对预习作业的及时训练和深化认知。其中部分题目还选自学生自行设计的复习题,上课时极大的激发了学生的学习热情。
(四)课堂上教学学案和预习作业形成“问题链”,进行深化探究
授课过程中,课堂伊始由学生代表对预习作业进行分析,并针对总结的易错点进行全班讨论解决,并进行方法、思想总结。然后由学生代表展示小组内设计的变式复习题,或在教师提供的问题情境或学习资料下,对课堂学案中和预习作业相关的“问题链”进行深化探究。对变式问题或典型例题的探究可以充分发挥自主探索与小组讨论相结合,生生合作,师生合作等形式,充分发挥学生的主观能动性。
在学生们合作讨论的同时,教师在教室内巡视各小组对问题的解决情况,并及时收集学生在讨论中不易解决的知识、思维习惯、易错点等,以便恰当准确的引导学生分析和探究。在小组讨论后,由学生代表给出讲解,教师从旁引导,然后其他同学可以讨论、争辩、补充、一题多解等,充分发表自己的意见,在讨论中不断简化问题、解决问题,从而使学生的发散思维得到锻炼。在问题解决后,学生们自行归纳知识点、数学方法和数学思想。教师可从旁点拨。
以笔者在“数形结合思想在二次函数解题中的运用”的教学实践为例,我们来看课堂授课中课堂学案和预习作业的“问题链式深化探究”的实现。
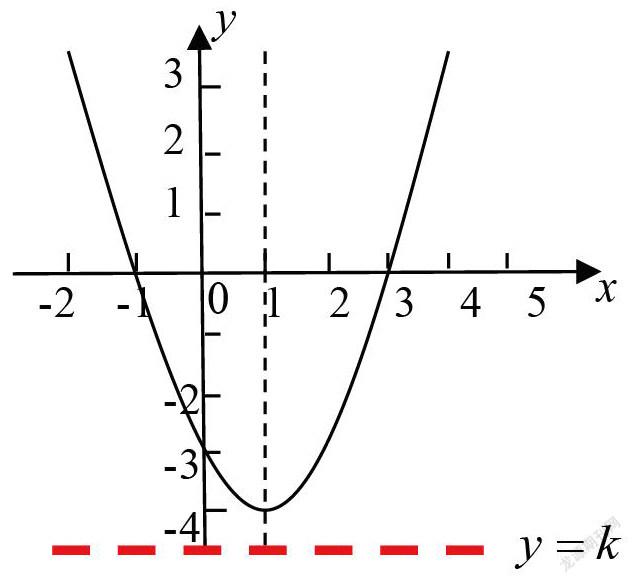
如对预习作业5和例四的处理,首先由学生代表积极讲解预习作业5:已知方程有两解,求实数k的取值范围。在同学们的讨论、争辩与补充,以及教师点拨下,涌现了多种解法。如方法一:数形结合,将的解看做函数与函数的交点的横坐标,利用两个函数交点的个数判断方程的解的个数,如图,当函数位于二次函数图像最低点的上方,即时,两个交点,此时方程有两解。方法二:方程的思想,将方程变形为,方程有两解则得到.
此时教师应及时点拨,让学生体会函数与方程的思想,理解一元二次方程与二次函数的联系,并归纳方法。还可以追加变式提问:k取何值(1)方程有一解?(2)方程无解?然后分小组讨论解决,并解决课堂学案中的例4 .在小组合作解决例四过程中,教师可以观察学生掌握情况,点拨大家思考对解析式整体加绝对值对函数图像造成的变化。讨论后由学生代表給出正确讲解。
接下来,我们将预习作业5中的“=”变为“>”,延伸得到了预习作业6。已知不等式对任意恒成立,求实数k的取值范围.学生自然会将预习作业5的解法与预习作业6的解法类比应用起来。在班级的热烈讨论和教师的点拨中,同样涌现了多种解法。
方法1: 数形结合,二次函数图像位于函数图像的上方,观察图像可得.方法2:最值法:要使不等式对任意恒成立,k小于二次函数的最小值即可,利用顶点坐标得到函数最小值.方法3:函数与方程的思想:将变形为恒成立函数的函数值大于零恒成立函数与x轴无交点方程无解.
教师及时点拨学生合作讨论并归纳二次函数、一元二次方程、一元二次不等式的关系,明确和渗透函数与方程思想及数形结合思想。并体会利用图像、最值或分离变量法解决恒成立问题的方法。在此基础上对例5进行合作解决.
在这种递进的链式问题探究下,学生由易到难,并通过合作讨论吸取其他学生的思路,然后及时借助于例题快速对所学进行测验和复习,从而建构起自己的数学思维。
(五)教师点拨、学生合作形成本节课的知识网络
经过预习作业和课堂学案的解决,在教师的引导下,由学生对本节课的知识要点进行总结归纳,包括重点知识点、数学方法、数学思想等。归纳的形式可以是表格、树状图、思维导图等等多种形式,学生们可以对学生代表展示的归纳结果进行讨论、指错和补充。
教师对各小组的表现给予评价,并对典型知识进行强调和点拨,深化学生们的知识结构认知。
(六)课后探究作业与课堂教学链式结合,培养综合应用能力
课后探究作业的设置也要与课堂学案上的典型例题形成“问题链”,题目的选择除了教师对本节课重点的把握和加强练习而设计的题目之外,也可以从课前收集的学习小组自行设计的题目中选择,从而激发学生的设计热情。而且在授课后教师可以针对课堂上学生们的整体把握情况,对课后探究作业内容进行及时调整。
四、“问题链探究式”生本复习课的优势及建议
“问题链探究式”生本复习课的优势在于给了学生充分从事数学活动的机会。通过预习作业,将学生的“学”放在教师的“教”之前,在课前引导学生进行主动探究,学生甚至可以自行设计复习题。在学习过程中,发挥学生的主体地位,改变传统复习课教师填鸭式知识点的灌输方式,改为学生主讲。学生并不是被动的信息接收者,而是知识的主动建构者,他们合作需求解决问题的最佳方法,并自行归纳总结。教师的主导作用体现在创设最佳的教学环境,比如预习作业与课堂内容设计巧妙的问题链,又或者巧妙的激发学生进行热烈讨论,营造民主氛围,抛砖引玉激发学生思路,归纳总结时重点进行点拨等。
当然“问题链探究式”生本复习课也有其局限性,并不是所有的教学内容都能找到合适的问题链。具体授课中需要教师根据教学内容和学情,选择最适合学生的方式。
参考文献:
[1]《普通高中数学课程标准》
[2]《在高中数学复习课中如何进行问题探究》——孙刚
[3]《基于案例分析的初中数学复习课问题研究》——孙月梅

