浅谈几何易错题在初中数学反思性教学中的实践
刘新泉


摘 要:在初中数学的教学中,易错题是最值得关注的一类问题。平面几何以其考察能力广,数学思维要求高,在初中数学课堂教学中占有重要地位。所以对平面几何易错题的研究利用对于提升学生数学能力有着深远的意义。本文试图从教学实践出发,浅析几何易错题的有效利用方法。
关键词:初中几何;易错题;教学实践
初中几何学习中,学生在解题过程常出现错误是不可避免的,这对学生和老师来讲,都是很头痛的事。但这些错误的出现,给老师在课堂教学和研究中提供了绝好的素材。充分挖掘易错题这个宝藏,对老师的日常教学和学生的学习都有着积极的促进作用。以下谈谈笔者在教学实践中总结出的几个观点供大家参考。
一、巧用“易错题”,培养学生良好的解题习惯
在上纠错习题课堂上,我先把学生所做错题投在黑板上,让大家找出其中的错误之处。结果学生七嘴八舌地指出他证明中的各种错,我一一板书总结,渐渐的没有回答的同学了,我又问:还有错误吗?学生观察思考后才回答:题目中的结论“四边形ABCD是平行四边形”是不能用图形符号的。而且没有菱形的图形符号。而很多学生都会有这种随意书写的坏习惯。我在强调后,让学生写出正确的证明过程。然后点评。最后告诉学生:数学最重要的特点就是严谨.通过对错题的分析和点评,要求学生反复检查每一歩推理的正确性和表达准确性,培养学生慎重思考,仔细推理的良好习惯。
二、研究“易错题”,对学生的知识储备进行查漏补缺
在错题收集过程中,我发现有六,七个同学的证明过程出现如图所示的三角形全等的证明判定不会,对已知条件不能正确运用,圆中的性质不会用等错误。通过错题的研究,从学生出错的频率情况,我发现了班级学生知识储备和欠缺的知识以及对新知识的掌握情况,找到大家没有掌握好的知识点,然后进行针对性的反复强化训练和检测,对个别学生一对一辅导,直到学生掌握为之。也让学生看到自已的不足之处,从而进行更高效的进行学习。
三、挖掘“易错题”成因,发现知识的本质
在分析上面这道错题时,我们不难发现,它重点考察了“90°的圆周角所对的是圆的直径,直径所对的圆周角是90°”的性质,和正方形的判定定理。而判断AC,BD是圆的直径是要证明的。另外,巧妙地运用圆的半径和直径的关系,来证明四边形ABCD是平行四边形,最后我们还要清楚四边形是正方形的的所有判定定理。这道综合题,通过老师分析错因,层层剥笋,可以有效帮助学生分析理解圆的概念性质的内涵和外延,激发学生的探究解决综合题题的兴趣,增强问题意识,拓展思路,加深学生对问题本质的理解。有效地促进了学生对各知识点之间的融会贯通。
四、利用“易错题”,培养学生思维能力
在本题的点评中,我提问学生:“有几种方法可证明四边形ADCB是正方形?”点评完后,请学生们重新设计已知条件,仍可证明四边形ABCD是正方形。
于是学生给出了以下的设计:
已知:在⊙O中,AB=BC=CD=AD,证明四边形ABCD是正方形.
已知:在⊙O中,弦AC,BD是直径,且AC⊥BD,证明四边形ABCD是正方形.
已知:在⊙O中,弦AC⊥BD,且∠ADC=90°证明四边形ABCD是正方形.
从这些学生设计中,也可以看出学生对本节纠错题课内容的理解掌握情况。通过这一教学过程的设计,让学生找错误的源头并发展该问题,从而引导学生积极整理思维过程,使之条理化,精确化,慎密化,概括化。进一步培养学生举一反三,分析归纳和发散性思维能力。
五、巧用“易错题”,培养学生创新思维
在错题课堂上,学生出错率最高的是下面这一题的第二问,“判断△PAE的形状”,很多学生通过证明很容易得出“△PAE是等腰三角形”这一错误结论。具体题目如下:
如图,点P是正方形ABCD对角线BD上一点,连接PA,PC。
求证:∠PAB=∠PCB
在BC边上取一点E,使得PE=PC,连接AE,试判断△PAE的形状,并说明理由。
学生证明如下:
(1)证明:∵正方形ABCD
∴AB=BC ∠ABP=∠CBP
在△PAB和△PCB中
AB=BC
∠ABP=∠CBP
BP=BP
∴△PAB≌△PCB (SAS)
∴ ∠PAB=∠PCB
(2)△PAE是等腰三角形,
∵△PAB≌△PCB
∴PA=PC
又∵PE=PC ∴PA=PE
∴△PAE是等腰三角形。本题第2问,学生对△PAE的形状判断是错误的,学生思考很简单,由PE=PC,联想到由三角形全等,得出PA=PC,但忽略了第一问证明的结论∠PAB=∠PCB,更深入思考:第一问证明的结论和第二问有关系吗?通过分析知道:有关系。由结论:∠PAB=∠PCB
又∵PE=PC ∴ ∠PEC=∠PCB
∴ ∠PAB=∠PEC 又∵∠PEC+∠PEB=180°
∴∠PAB+∠PEB=180°又∵正方形ABCD
∴ ∠ABC=90°
在四邊形ABEP中 ∠APE=360°-(∠PAB+∠PEB+ ∠ABC)=90°再结合学生已证明得PA=PE
∴△PAE是等腰直角三角形。这才是一个完整的答案。
这反映了学生在几何题证明方面缺乏全面,深入细致的分析和推理。也反映了教师在教学中对这一类型的习题没有系统的思想指导,(例如,有两小问的题目,如果第一问的结论是由题目已知推理得出,那么第二问的证明是可以用第一问的证明结论的。)因此大多数题目1,2问是有关联的。学生的创新思维体现在把所证明的边的相等,以及角的转化从而证明顶角是90°,归纳得出△PAE是等腰直角三角形的正确结论。在教学过程中,学生不断出现的错误是再所难免,它反映了学生的真实想法和思维能力。这其中包涵了学生知识上的漏洞和老师教学上的不足。 因此,教师应当善于运用“错题”,善于发现错误被后隐藏的教学价值。 把“错误”巧妙地运用到日常教学中。弥补教学上的不足。此外,还要引导学生利用错题记录本,整理所有出错的题目,分析出错原因。
六、辩析数学概念,深入挖掘“易错题”的内涵,运用正确的几何解题策略
在2021年的中山市中考数学试题中有这样一道填空题:在△ABC 中,∠ABC =90°,AB=2 ,BC =3.点 D 为平面上一个动点,且∠ADB =45°, 则线段CD 长度的最小值为——。
这道题没有图,考查学生根据题意正确画出图(下转第4页)(上接第2页)形,学生要正确画出图形就要弄明白三个问题:
①动点D在平面內的什么图形上运动?和圆有关系吗?
②这个圆以什么为圆心?什么为半径?
③点D运动到什么位置时,线段CD最小?
要回答第一个问题,就需要深刻理解概念“在同圆或等圆中,同弧所对的圆周角相等”。本题中,点D在运动过程中,始终保持∠ADB =45°,说明∠ADB是圆周角,并且顶点D在圆周上运动。
对第二个问题的解答,本题挖了一个很大的坑,很多同学认为∠ABC =90°,所以这个圆是以AC为直径的圆,从而成功掉到坑里。事实上,仔细观察研究圆周角:∠ADB =45°,不难得出这个圆是以等腰三角形ABE的斜边AE为直径,AE的中点O为圆心的圆。
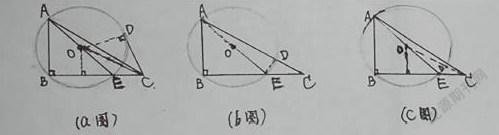
对于第三个问题,学生在成功画出图形后又犯难了,点D运动到圆周的什么位置时,线段CD才会最小呢?这里又出现两个易错点:a.当CD为切线段时最短;b.直角三角形ABC的斜边AC与圆的交点D时,线段CD最小;c.连接OC,与☉O的交点为在,此时CD最短。这三个答案,究竟谁对谁错?又考察了两个重要公理:①垂线段最短②两点之间线段最短。该用哪一个呢?,将三种情形画图如下所示:
仔细思考,只有c图是对的,考查了圆外一点与圆心的连线与圆的交点最短。不难计算出CD最小值的正确答案为 5 - 2 。好象a图和b图也有道理,但经不起概念的深入挖掘和推演,a图中的CD长为 3 ,b图中的CD长为 ,显然 5 - 2 比—的值大,通过比较三个结果,易得出正确结论,但通过仔细思考辩析三个相近的概念,也会得出圆外一点与圆心的连线与圆的交点最短。
在教学过程中,面对不同层次的学生,他们的知识储备有不同的深度和广度,有不同的思维水平和解题技能,出现五花八门的解题错误不可避免。我们教师只有在课堂教学中对概念教学要深挖,批改作业时不要忘记搜集学生的典型错误,及时进行成因的分析,整理,记录,并制定出有效的矫正策略,充分发挥“易错题”的积极作用。培养学生明辨析,深挖掘,勤反思的数学思维习惯,不断提升数学素养。
【本文系广东省中山市教育科研立项课题“基于几何易错题成因分析进行反思性教学的实践研究”的阶段性成果(课题编号:C2018099)】
参考文献:
[1]陆微微.初中数学典型易错题的分析与思考[J].现代中学生(初中版),2021(10):47-48.
[2]杨红云.初中数学“易错题”的有效利用方法[J].现代中学生(初中版),2020(24):46-48.
[3]朱铭.初中数学易错题的成因及解决对策[J].数学大世界(中旬),2020(12):12.
[4]张建金.浅谈初中数学易错题的成因及教学策略[J].中学生数理化(教与学),2020(11):58.
注释:
由于本文素材来源于教学实际,故采取照片形式绘图。
(作者单位:中山一中西区中学,广东 中山 528400)

