初中数学一元二次方程概念教学中“问题结构化”的尝试

罗玉封

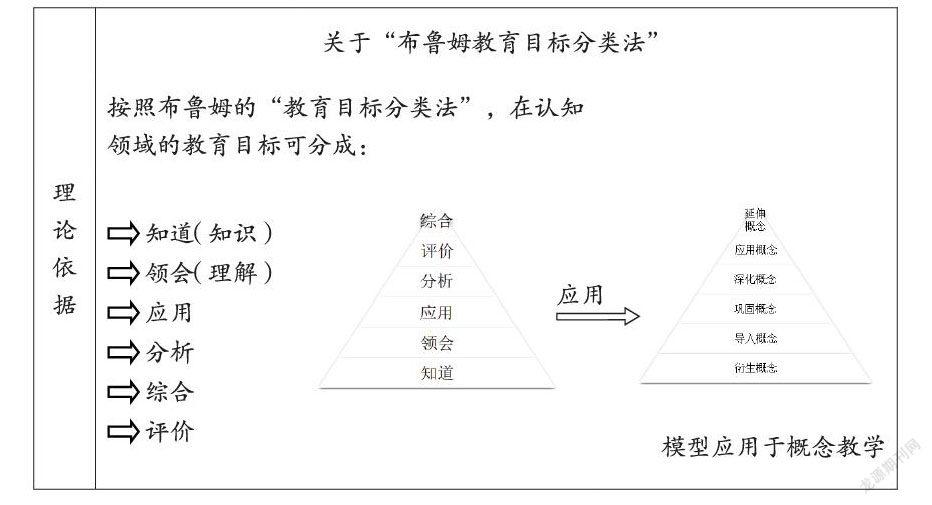
【摘要】本文以人教版教材九年级第二十二章《一元二次方程》中有关一元二次方程及相关概念的教学内容为例，按照《数学课程标准》的要求实施本章的概念教学的同时，尝试将概念理解按布鲁姆“教育目标分类法”的六个层次进行“问题结构化”：衍生概念、导入概念、同化概念、巩固概念、深化概念、延申概念，让学生在学习过程中体验、感受、理解这些知识的来源、生成和本质，从而提高学生提出问题、分析问题和解决问题的能力。

【关键词】初中数学;问题结构化;概念教学;一元二次方程;问题情景

《数学课程标准》指出，数与代数的学习不仅要使学生掌握必要的知识和技能，而且要使学生在学习过程中体验、感受、理解这些知识的来源、现实背景和本质，形成数感和符号感，认识数学与生活的密切联系，了解数学的价值，提高提出问题、分析问题和解决问题的能力。因此，数与代数的学习内容应当是现实的、有趣的、富有挑战性的。教师应该通过实际情景或问题情景使学生了解数与代数的意义，让学生经历探索和发现的过程，在问题情景下感受和体验有关的知识。一元二次方程是初中“数与代数”部分的重要概念之一，在中考命题中有着不可或缺的地位。它是方程及一元一次方程内容的再发展，同时，也是后续学习二次函数的前提与基础，在初中“数与代数”部分的教学内容里担当着承上启下的作用。

根据布鲁姆“教育目标分类法”及学生认知规律，本节概念教学过程分为六个步骤：衍生概念、导入概念、同化概念、巩固概念、深化概念、延申概念，并进行“问题结构化”，助力学生对概念教学理解的深度、广度和高度。

一、衍生概念，类比尝试

一元二次方程是初中学段“数与代数”部分中的重要内容，也是历届中考的热门考点之一。熟练掌握一元二次方程及相关概念，对于整个方程这一知识版块的理解和认识会得到进一步的巩固和加深，同时也为后续有关函数的内容的学习尤其是二次函数的学习会起到重要的基石作用。

数学概念就是反映思考对象空间形式和数量关系本质属性的思维形式，一元二次方程与先前所学习的方程和一元一次方程的有关知识联系密切，将三者的主要内容放在一起进行对比学习，将三者之间的区别与联系展现给学生，从而使得学生对方程的概念能从一元一次到一元二次形成认知上的类比迁移。一元二次方程是在对方程已有认识的基础上的发展，根据这一特点设计衍生概念的问题情景：

我们了解方程的概念吗？

我们了解方程的解的概念吗？

我们了解的概念是从哪里得到的？

例1：

1.含有_____的等式叫做方程。

2.只含有___个未知数，且含有未知数的项的次数都是_____，这样的方程叫做一元一次方程。

3.使得方程中等号左右两边相等的未知数的值，叫做方程的_____。

通过复习回顾方程及一元一次方程的有关概念，为衍生出一元二次方程及相关概念奠定基础。同时，用对比教学的形式上，采用列表格的形式来凸显本课的教学内容实现概念间的衍生观。

例2：

以上概念的描述对于学生而言比较抽象。而且，还有系数等概念还需要具体地加以说明。这两个概念是建立在初一上学期学习“一元一次方程及一元一次方程的解”的基础上对方程学习的再发展，目的是希望在课本教材的基础上进行丰富和优化，让学生经历探索和发现的过程，在问题情景下感受和体验一元二次方程概念。因此，在实际教学过程中，教师抓住了这些概念的内涵与外延，结合实际问题情景，给予学生体验感知发现的机会。这样，学生才能快速把握一元二次方程及相关概念和系统掌握一元二次方程的相关知识。

二、导入概念，设置操作与问题情境

人教版教材在第二十二章《一元二次方程》的引言中提出了一个关于制作无盖方盒的问题，以此为现实背景引出本课的有关一元二次方程的概念。在此基础上设置了一个制作无盖小纸盒比赛为背景的实际操作情景，并考虑到本课的重点和可操作性，因此将落脚点放在列方程这一环节上，对问题中的等量关系寻找给出了提示，并在学生列出方程后，提出问题让学生对所列方程和一元一次方程进行比较，思考其不同点。

例3：班级即将举行制作无盖方盒比赛，每位参赛选手将拿到一块长方形纸皮，长10cm，宽5cm，在它的四角各切去一个同样的正方形，然后将四周突出部分折起就能制作一个无盖方盒，如果要制作的无盖方盒的底面积为36cm2，那么各位选手应在纸皮各角切去多大的正方形？

分析：设切去的正方形边长为xcm，则盒底的长为_____cm，宽为_____cm，根据_____×_____=长方形面积，列出方程得：__________，整理、化简得：___________。

例4：根据问题1的内容列出的方程有什么特点？与之前学的一元一次方程有什么不同？____________________

分析：任何一个概念都不是孤立的，一些概念之间往往有着十分紧密的联系，对那些相近或相似关系的概念，因为它们有着诸多的相似，所以用类比的方法进行教学，产生类比构建的良好思维习惯。类比的方法不是严格的数学证明方法，它是根据事物间的共同特性，由一事物研究另一事物的思维方法，可以作为概念教学的情境创设方法。同时，让学生在动手操作过程中体验、感受、理解这些知识的来源、生成和本质，提高提出问题、分析问题和解决问题的能力。

解決了上述问题后，导入本课的一元二次方程的概念，以填空的形式让学生自主完成：

概念1：等号两边都是_____，只含有_____未知数，并且未知数的最高次数是_____的方程叫做一元二次方程。

当学生得到了这个新的概念后，笔者设计导入概念的问题情景：

一元二次方程概念核心要素有几个？

一元二次方程概念理解的关键是什么？

一元二次方程概念一般形式中哪个知识点是我们最容易遗忘也最容易出考题？

一般形式中如果a=0会怎样呢？

然后，学生要抓住概念的关键词——1个未知数，未知数的最高次数是2，整式方程，一般形式：ax2+bx+c=0（a ≠0），一次项、一次项系数、常数项等概念，关键是整式方程。特别解释，a≠0是最容易遗忘也最容易出考题，让学生更深入地去感受和理解概念。

三、同化概念，题组练习

在概念的同化阶段，主要采用题组练习的方式进行，题组的设计由浅入深，让学生同化概念的同时转化为对知识的应用与操作技能的提升。

例5：下列方程中，是一元二次方程的是（ ）

A.  2x2-=0      B.  y2+x=1

C.  x2+1=0          D. （x+1）2+5=x2

例6：将下列方程化成一元二次方程的一般形式，并写出其中的二次项系数、一次项及常数项：

（1）5x2-1=4x    （2）4x2=81      （3）4x（x+2）=25

练习3 填空

（1）关于x的一元二次方程（m2-9）x2+（m-3）x+5=0，m=_____时是一元二次方程;m=_____时是一元一次方程。

（2）m=_____时，（m+1）x|2m|+5mx-1=0是关于x的一元二次方程。

经过上述的题组练习，让学生进一步加深对一元二次方程的认知和同化。特别是二次项系数a≠0这一要求，这是学生在平时比较容易忽略的知识点。

四、巩固概念，具体入抽象

当然，在这一环节的教学中，笔者也遇到了一些困惑和问题。在本次教学中，课本对于二元一次方程是整式这一内容没有加以说明，有的学生也容易忽视这一方面，这样便会在面对形如本文练习1中所提到的2x2-=0误判其为一元二次方程。值得说明的是，在解释该方程不是一元二次方程时，笔者一开始是想通过说明方程中所含有x的项 ，其实可以写成x-1，由于其次数是-1而不是1来说明，即让学生掌握“整式”这一关键点，学生在此处容易犯错。在本文练习1中所提到的（x+1）2+5=x2也容易让学生误认为是一元二次方程。在这一练习讲解时再次提及a≠0，有必要的话加大题组的题量或在课后作业中进一步巩固。

简而言之，笔者认为，教师应该要设想学生在接受新知和利用新知解决问题时所可能出现的状况，有了这方面的心理准备，那么不论是在课前扫清学习新知的障碍，还是在学生学习过程中遇到挫折后再扫清障碍，都可以做到有的放矢，掌控自如。

五、反思操作，深化概念

一元二次方程的解的概念，教材是利用一个表格让学生自主探究进而给出的。但是，经笔者思考并在教学实践中发现，如果完全按照课本教材进行讲解，学生的合作交流的程度不够，且因学生的个体差异，导致有的学生很快完成探究，而有些学生却不知所以然，使得课堂教学进度不一，效果较差。因此，针对这一情况，笔者采用类比迁移的方法由已经熟悉的一元一次方程的解类比得到一元二次方程的解：“使得方程中等号左右两边相等的未知数的值，叫做方程的解”，这一概念在一元二次方程的解中同样适用。这样，学生能进行知识的类比迁移，对新知識的吸收更快，而且笔者设计了以下练习用以巩固学生对方程的解的概念进行深化认知。

例7：下面哪些数是方程x2-3x+2=0的解？为什么？

-1，0，1，2，3

例8：已知x=-1是方程x2+mx+1=0的一个根，求m的值。

例9：一个长方形的长比宽多1cm，面积是132cm2，长方形的长和宽各是多少？

第一、二道练习的设计目的主要是巩固一元二次方程的解的概念，第三道练习的设计目的是为了进一步说明一元二次方程是刻画现实世界的重要数学模型，与课堂引入的例子进行呼应，同时也为后续关于一元二次方程的解法的学习设置一个铺垫。

当学生完成练习后，采用深化概念的问题情景引导学生思考总结本课所学内容，说出感受和收获。这样，学生通过这节课的学习不仅掌握了一元二次方程的概念，而且能快速地判断哪些是一元二次方程的解。

深化概念的问题情景：

一元二次方程的概念与一元二次方程的解的概念是什么？

两个概念的意义是什么，两个概念的作用是什么？

一元二次方程的概念与一元二次方程的解的概念怎样获得，你下次会用类似的方法解决问题吗？

六、延伸概念，实施课例后的思考

一元二次方程是刻画现实世界的数学模型之一，它来源生活实际，体现出数学的建模思想。在概念教学过程中，对这一概念导入也是通过实际问题的提出而进行的，在生活中还有很多例子只用一元一次方程是没法解决的，必须利用一元二次方程相关问题设置，让学生在思维上产生认知冲突。故教学时，教师应让学生体会学习一元二次方程的价值，让学生初步建立数学模型的思想，初步学习如何将实际问题转化为数学问题转化思想;并设置问题情景让学生产生联想和串通，将概念向更深更高更广的层次延申，延申概念的问题情景：

解一元一次方程的过程有几个步骤？

能不能将一元二次方程转化为一元一次方程来解呢？

大家还记得因式分解的过程吗，它能给你什么启发？

最后，本节概念课教学通过结构化问题与问题情景的设置也培育学生的数学核心素养——数学抽象素养、数学运算素养、发现问题、分析问题、解决问题等多层次的数学能力。

参考文献：

[1]教育部.数学课程标准[S].北京师范大学出版社，2011.

[2]（美）B·S·布鲁姆等.布鲁姆等教育目标分类学第一分册：认知领域[M].华东师范大学出版社，1986.

[3]中学数学课程教材研究开发中心.数学九年级上册教师教学用书[J].人民教育出版社，2009.

责任编辑  钟春雪