圆柱波导并矢格林函数的构建及其在圆柱腔中的应用
雒向东,赵宇杰,海 波,梁 晔
(1.兰州城市学院 a.电子工程学院;b.信息工程学院,兰州 730070;2.甘肃高师学报编辑部,兰州 730070)
自Hansen首次引进矢量波函数用来解决某些电磁问题[1-3],Stratton验证了这些函数的有效性[4],这些函数的使用方法进一步被Stratton、Morse[5]等有所推广,戴振铎[6]、宋文淼[7]、柯享玉[8]等就电磁理论中的并矢格林函数做了大量研究,使得并矢格林函数(简称DGF)方法被广泛应用于电磁理论及工程的各个领域。用DGF方法解决各种电磁场工程问题,其关键是要求出DGF表达关系,因此DGF的求解和研究自然成为学者关注的热点问题。国内外学者对构建矢量格林函数做了大量研究,如对规则形状波导、常用坐标系等问题已有一致的结果,有些问题如圆柱腔问题报道文献就比较少[9-13]。该研究就圆柱腔驻波波函数、圆柱波导并矢格林函数的构建及其在圆柱腔中的应用进行探索,研究结论可为基于DGF方法解决圆柱波导及圆柱腔电磁场边值问题等提供理论和技术支持。
1 构建圆柱坐标系驻波矢量波函数


图1 圆柱波导
在圆波导内研究齐次标量亥姆霍兹方程,假设波沿z轴方向导行,沿φ,r方向均为驻波,其基本标量波函数可表示为[14]
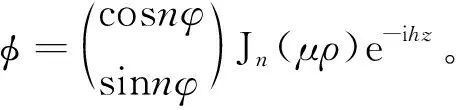
(1)
式(1)中,除n=0情况外,每一组分离常数对应两种不同极化场的模式,称为模式极化简并。
基于圆柱坐标系中的标量波函数,定义两类圆柱矢量波函数,它们在r=a时都满足矢量狄里克莱边界条件。两类圆柱矢量波函数定义为[6]104-114
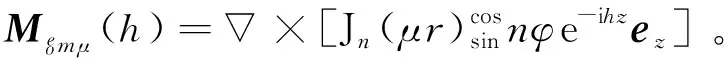
(2)
其中:
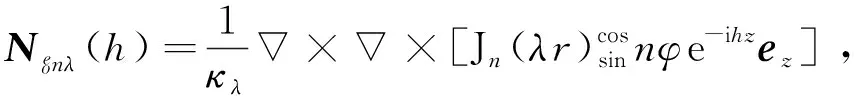
(3)

式(2)和(3)矢量波函数的完全表达式为
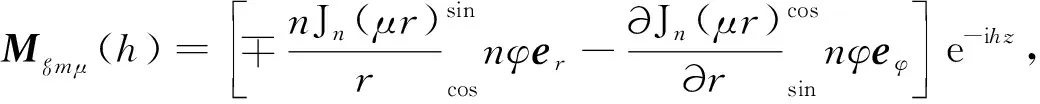
(4)
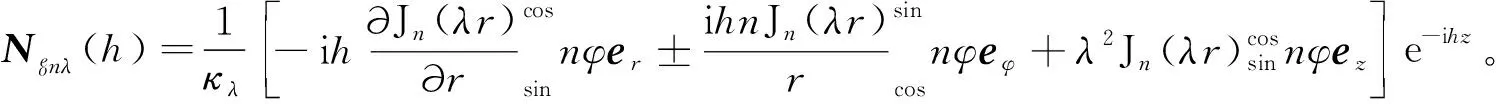
(5)

描述圆柱波导中的磁场,可采用的矢量波函数为

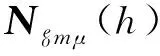
另外,矢量波函数之间还存在如下关系:
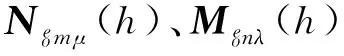
基于两类圆柱矢量波函数,构建两个驻波矢量波函数,用Mμo(z)和Nλe(z)分别表示,其形式为
(6)
(7)
2 圆柱波导并矢格林函数
(8)
其中,求和指数m、n与关系式pnm=λa和qnm=μa相联系,可简化记为
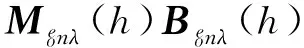
用Nonμ(-h′)、Menλ(-h′)和Monλ(-h′)分别与式(8)作前标积,可分别得到系数为
这几个系数可简写为

(9)
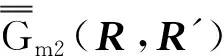
(10)
将式(9)和(10)代入并矢格林函数满足的麦克斯韦方程[15]
可求出a、b系数为
(11)
将式(11)代入式(10)得


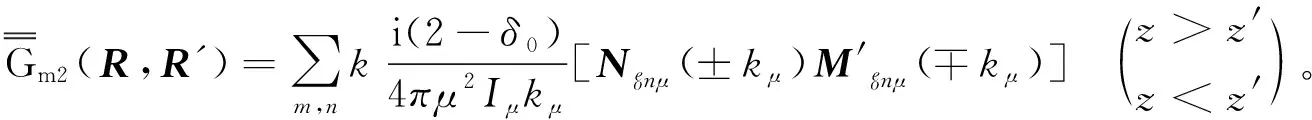

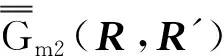
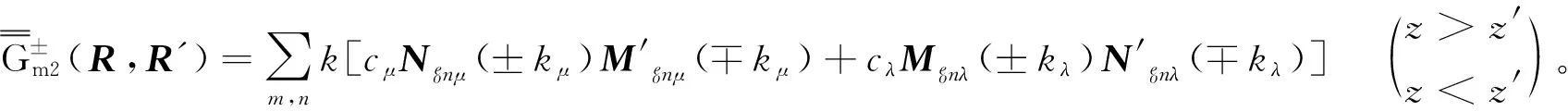
(12)
其中:
(13)
kμ、kλ表示两组模式相应的导波函数,式(12)中上行符号对应z>z′,下行符号对应z 其中: 可推得边界条件为 (14) (15) (16) 式(16)中使用了两个单位阶跃函数,它们是 进一步推得式(15)为 (17) 由广义函数理论知 U(z-z′)=ezδ(z-z′) ,U(z′-z)=-ezδ(z-z′) 。 (18) 将式(18)代入式(17)得 (19) 利用式(14),式(19)又可写成 (20) 式(20)对于所有ρ,φ,z值都适用,由于δ(ρ-ρ′)δ(φ-φ′)δ(z-z′) =δ(R-R′),把式(20)代入式(15)得 (21) 将式(12)代入式(21)得圆柱波导第一类电型并矢格林函数为 (22) 式(22)中上行符号对应z>z′,下行符号对应z (23) (24) (25) (26) 代入定义的相应矢量波函数,由式(26)可推得 Aμ=-1。 (27) 考虑代表TM模电场的一对波函数,满足在z=0处的狄里克莱边界条件为 (28) 同样代入相应矢量波函数可推得 Bλ=1。 (29) 将式(27)(29)代入式(25)得散射项为 (30) (31) 其中: (32) (33) 代入式(6)和(7)驻波矢量波函数,式(32)和(33)可简化为 (34) (35) 还可推得 (36) (37) 将式(34)至(37)代入式(31)得 (38) 其中: 这就是半无限长波导的第一类电型并矢格林函数表示式。 (39) (40) (41) (42) 由式(41)和(42)可求出 (43) 将式(43)代入式(40)得散射项为 (44) 将式(38)(44)代入式(39)得 (45) 其中: (46) 式(46)可化简为 sinkμcMμ(kμ)-e-ikμcMμo(z)=Mμo(c-z)。 (47) 同理,有 (48) 式(45)中有 (49) 式(49)可化简为 -iNλ(kλ)sinkλc-e-ikλcNλe(z)=-Nλe(c-z)。 (50) 同理,有 (51) 将式(13)(47)(48)(50)(51)代入式(45)得 (52) 这就是圆柱腔的第一类电型并矢格林函数。 当激励频率等于腔体谐振频率时 kμc=nπ,n=0,1,2,… 此时圆柱腔产生TEnm模式电谐振。 当激励频率满足下述关系时 kλc=nπ,n=0,1,2,… 此时圆柱腔产生TMnm模式电谐振。 利用圆柱坐标系中矢量波函数,研究圆柱波导系统并矢格林函数,构造圆柱腔驻波波函数,基于散射叠加原理推证圆柱腔第一类电型并矢格林函数关系,就谐振腔谐振问题进行研究。所得结论可为研究圆柱腔其他类型并矢格林函数以及腔内场结构等问题提供理论依据和技术指导。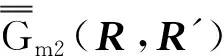

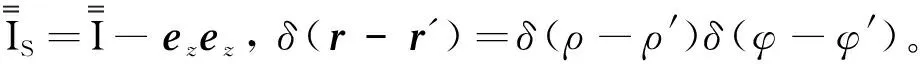


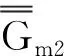


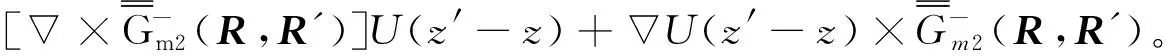



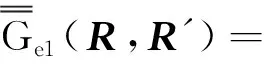
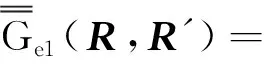

3 圆柱波导并矢格林函数在圆柱腔中的应用
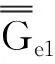
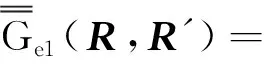

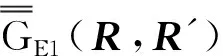


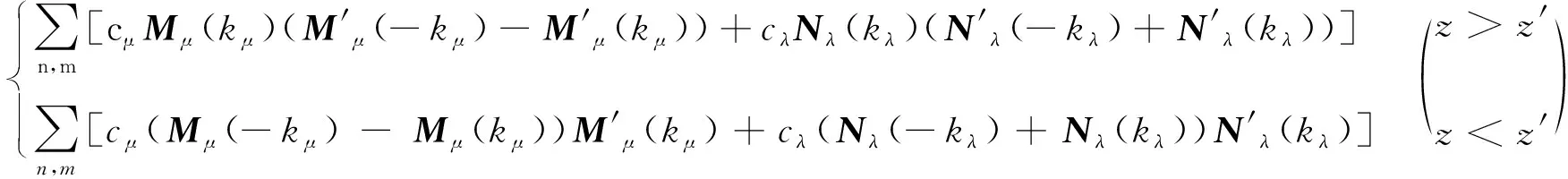



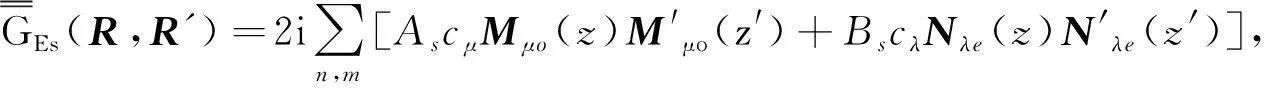

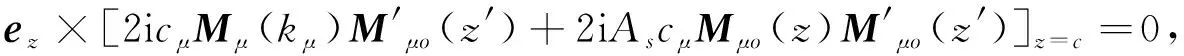
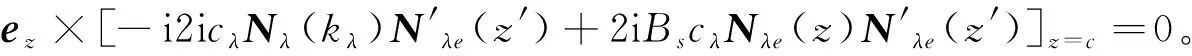
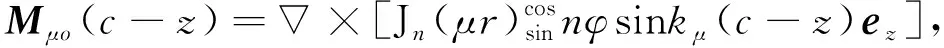


4 结语

