基于滑模理论的高速车辆侧风稳定性控制研究*

梁宝钰，汪怡平，刘 珣，张倩文，熊建波，胡兴军，王靖宇

（1.武汉理工大学汽车工程学院，武汉 430070；2.武汉理工大学，现代汽车零部件技术湖北省重点实验室，武汉 430070；3.吉林大学汽车工程学院，长春 130025）

前言

近年来，随着汽车轻量化、汽车高速行驶时间占比增加以及跨海大桥、高桥隧比高速公路的修建，侧向风对汽车行驶安全的影响越来越大。此外，随着汽车智能化的发展，对高速侧风稳定性的主动控制也提出了新的要求。改善车辆侧风稳定性的主动控制方法主要有主动前轮转向控制（active front steering，AFS）、主动悬架控制和直接横摆力矩控制（direct yaw-moment control，DYC）。其中，DYC 系统可以控制车辆纵向力分配以产生附加横摆力矩，特别是车辆侧向力饱和时，转向控制效果较差，DYC系统仍可以维持车辆稳定性。

针对DYC 系统，研究人员提出了多种控制算法，如门限值法、比例-积分-微分（PID）控制、神经网络控制等。滑模控制由于其滑动模态可以设定为与被控对象参数及扰动无关，故对系统干扰和参数摄动具有较强的鲁棒性和完全自适应性。受到扰动的高速车辆在基于滑模变结构理论的DYC 系统下，可以获得更多的稳定性控制效果。

本文中基于搭建的汽车多体动力学（multi-body dynamics，MBD）和计算流体力学（computational fluid dynamics，CFD）双向耦合控制平台，针对高速车辆侧风稳定性问题，提出一种基于滑模理论的车辆侧风稳定性控制系统，分析了在阶跃侧风下DYC车辆和未受控制车辆的动力学响应、气动特性和高速车辆车身周围流场的瞬态特性。

1 计算流体力学仿真

1.1 流动控制方程

汽车为低马赫数运载工具（＜0.3），侧风环境下的高速汽车周围的气流流动是瞬态变化的，因此该流场为非定常、不可压缩流场。汽车外流场雷诺数高达10，是充分发展的湍流流场。本文中选用Realizable-模型，它能更好地模拟剪切流和旋转流，被广泛应用于各种类型的流动模拟中。

1.2 计算域和网格划分

车辆运动速度通过重叠网格技术实现。重叠网格采用一组固定背景网格和一套运动受体网格，在不同的两个区域间传递计算信息。在运动对象周围建立一个小体积的规则“盒子”，称为重叠区域，计算域中除重叠区域外的其他部分称为背景区域。在数值模拟过程中，侧风下的高速车辆会发生纵向和侧向移动，故计算域尺寸应足够大，计算域总长为48.5 倍车长，宽度为15 倍车宽，高度为7.5 倍车高。计算域中车辆和其周围的长方体壁面为重叠区域，重叠区域总长为3.5 倍车长，总宽为5 倍车宽，高度为3 倍车高。计算域左侧为速度入口，右侧为压力出口，前后两侧为Symmetry 边界，顶部和底部为Wall边界。计算初始时刻的重叠区域在整个计算域中的相对位置如图1所示，为车长，为车宽。

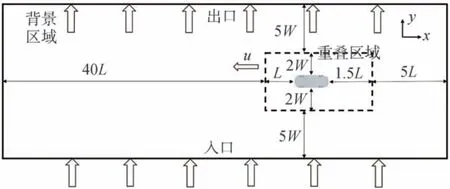
图1 计算域示意图

为准确模拟车身周围流场并减少网格数量，采用局部网格加密的方式减少网格数量。计算域网格如图2所示。车身周围网格尺寸为30 mm，边界层网格总厚度16 mm，层数为4 层，重叠区域加密尺寸为100 mm，重叠区域网格主体尺寸为200～220 mm，背景区域加密尺寸为240 mm，背景区域网格主体尺寸为800 mm。在使用重叠网格时，单位时间步内，重叠网格移动的距离应小于最小网格尺寸，故时间步长设为0.001 s。为保证空气动力学和汽车多体动力学模型中的气动六分力作用位置一致，空气动力学模型计算获取的气动六分力均基于车辆车身质心位置。

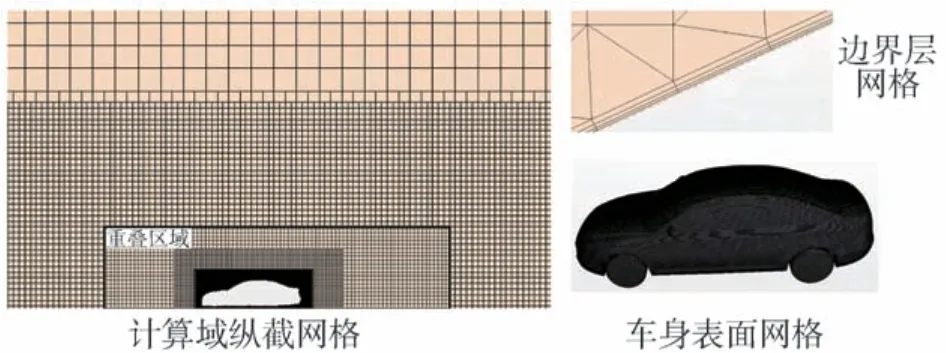
图2 计算域网格

1.3 单车外流场数值模拟验证

在湖南大学风工程试验中心，测量1∶3 缩比的轿车模型的气动阻力系数，通过与瞬态数值模拟的气动力系数时均值对比来验证所采用瞬态数值模拟方案的准确性。

风洞试验测量得到零偏航角下的气动力系数，如图3所示。风速范围为20～40 m/s，每隔5 m/s采集一次数据，共5组。数值模拟采用重叠网格技术赋予车辆速度，运动的车辆撞击静止空气，相对速度与风洞试验一致。

图3 风洞试验轿车模型

图4 为数值模拟得到的不同车速下气动阻力系数的时均值与风洞试验测量值的对比曲线。风洞试验的气动阻力系数平均值约为0.261，数值模拟的气动阻力系数平均值约为0.256，误差为2%，说明该数值模拟方案具有较高精度。

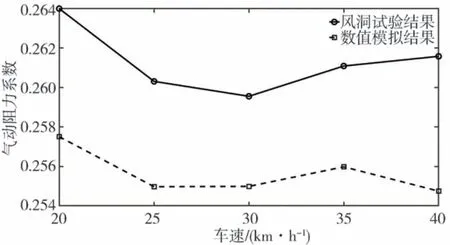
图4 风洞试验与数值模拟对比

2 汽车多体动力学仿真

在ADAMS/Car 中建立车辆动力学模型，包括车身系统、前后悬架系统、转向系统、制动系统及轮胎系统，如图5 所示。车辆整车参数如表1 所示，路面附着系数为1，轮胎模型采用基于魔术公式Pacejka89 的模型。该模型有68 个运动部件，160 个自由度，能真实地反映车辆的运动状态。在侧风稳定性计算中，车辆转向盘为锁死状态，空气动力学模型计算得到的气动六分力加载到车辆车身质心上，汽车多体动力学模型计算的时间步与空气动力学模型保持一致，为0.001 s。

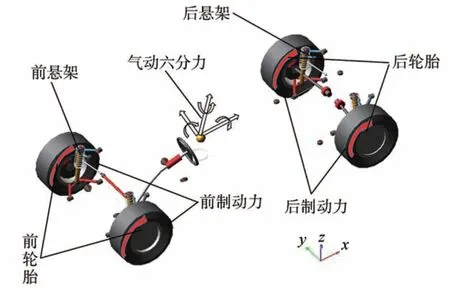
图5 整车动力学模型

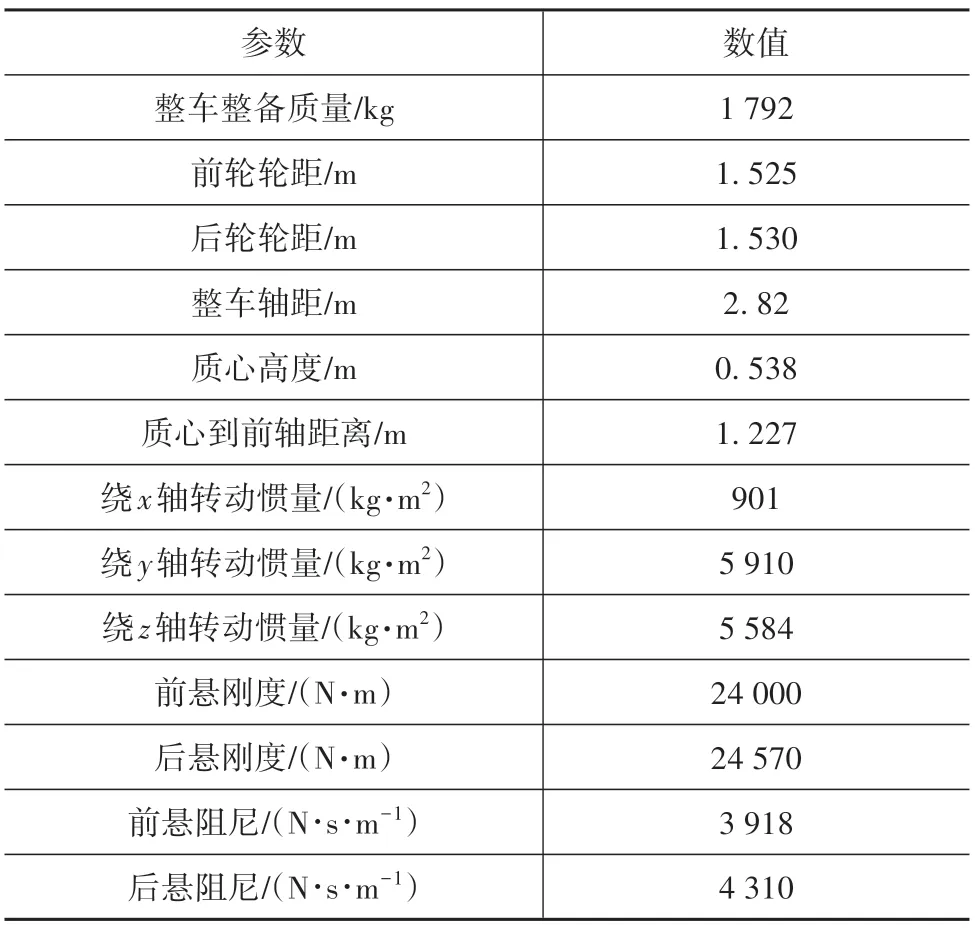
表1 整车参数表

3 CFD-MBD双向耦合控制平台

本文中通过CFD 求解器STAR-CCM+、MBD 求解器ADAMS/Car 和MATLAB/Simulink 搭建双向耦合控制平台。其中，空气动力学模型、汽车多体动力学模型分别通过CFD 和MBD 求解器计算，侧风稳定控制系统在Simulink 中搭建，并编写了接口程序实现求解器之间的实时数据交换。

CFD-MBD 双向耦合控制平台计算过程如图6所示。空气动力学模型和汽车多体动力学模型在耦合前独立计算0.2 s，当气动力和动力学响应趋于稳定并收敛后，开始空气动力学模型、汽车多体动力学模型和Simulink 控制模型间信息交互。空气动力学模型计算的气动力、力矩和Simulink 控制模型中计算的各个轮胎制动力矩作为汽车多体动力学模型输入，利用这些输入数据进行车辆动力学响应计算。然后给出车辆纵向速度、侧向速度和横摆角速度等动态响应作为空气动力学模型和Simulink 控制模型输入，并在空气动力学模型中更新车辆运动状态。在新的车辆运动状态下，再次通过空气动力学模型和Simulink 控制模型计算车辆气动力、力矩和各个轮胎制动力矩，完成整个CFD-MBD 双向耦合控制循环。

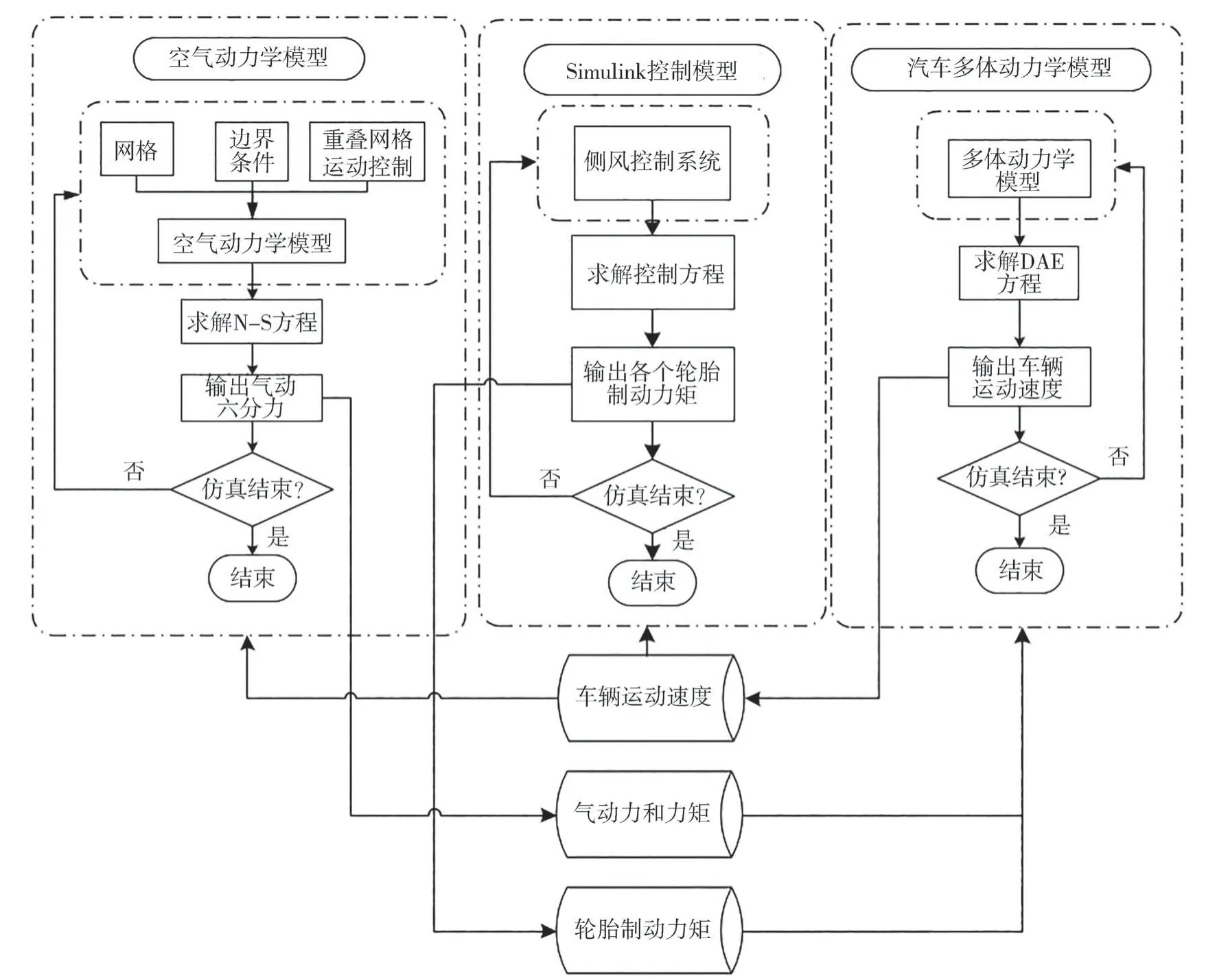
图6 CFD-MBD双向耦合控制流程示意图

4 基于滑模理论的侧风稳定性控制系统

4.1 侧风稳定性控制系统结构

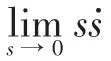
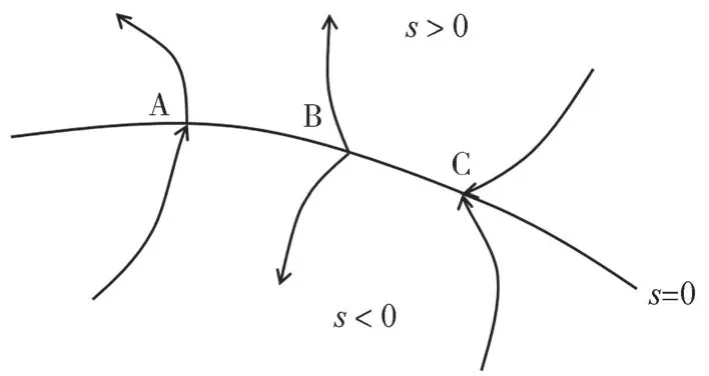
图7 滑模运动的切换面

基于滑模理论，设计了侧风稳定性控制系统（如图8 所示）。该系统为闭环控制系统，车辆横摆角速度为控制变量，车辆实际横摆角速度与理想横摆角速度之差为反馈变量。通过上层控制器计算出侧风干扰下的高速车辆为维持稳定所需的附加横摆力矩，下层控制器将上层控制器输出的横摆力矩分配至各个车轮，从而保持车辆稳定。

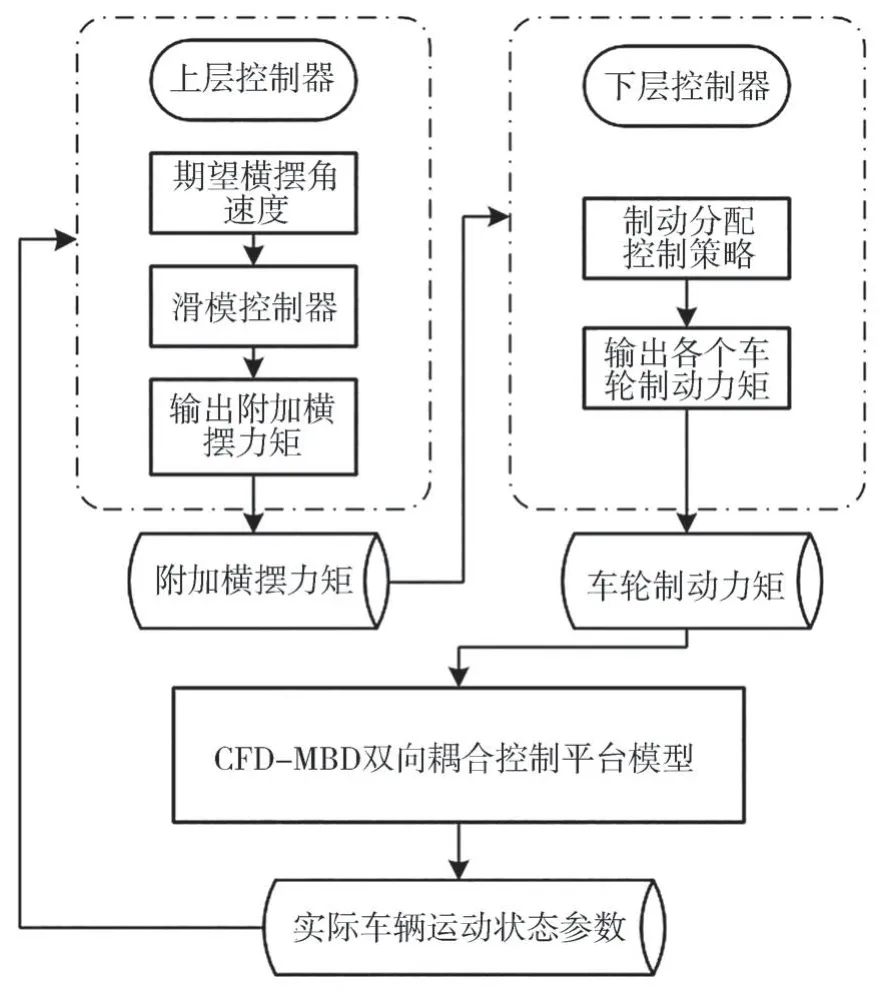
图8 侧风稳定性控制系统结构图

4.2 上层控制器

强侧风作用下，高速车辆常常出现侧向偏移和横摆现象。因此，当上层控制器计算的侧风干扰下的高速车辆为维持稳定所需的附加横摆力矩时，采用包含车辆侧向速度和横摆角速度的2 自由度汽车参考模型，如图9所示。

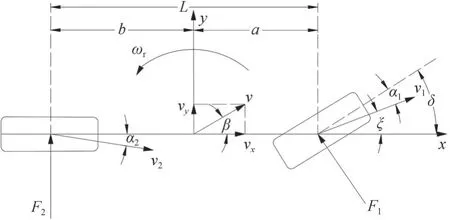
图9 车辆2自由度模型

考虑附加横摆力矩M的线性2自由度模型的状态方程为

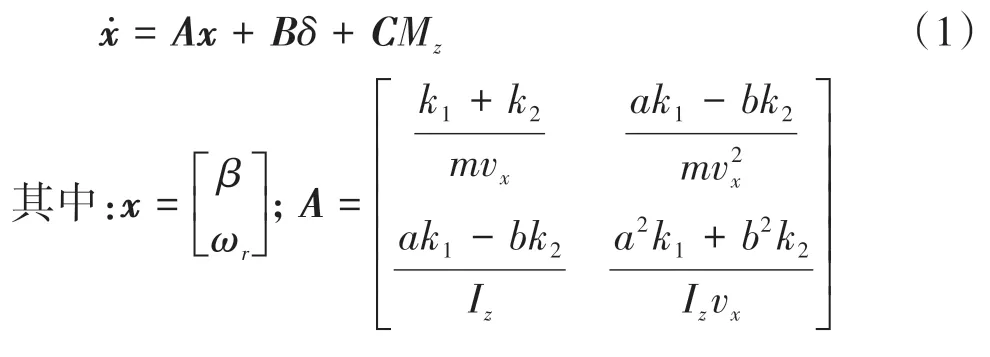
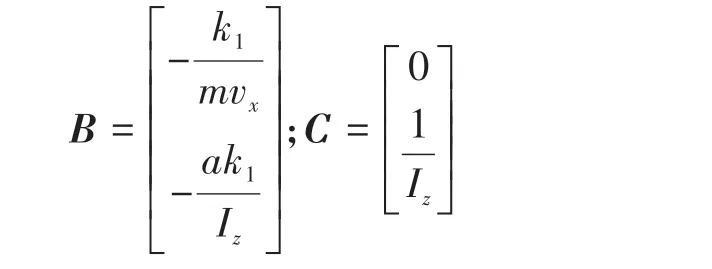
式中：、为前后轮的侧偏刚度；为质心侧偏角；为前轮转角；v为车辆方向速度；M为附加横摆力矩；为质心到前轴的距离；为质心到后轴的距离；I为车辆沿轴的转动惯量。

考虑侧风等扰动，由式（1）可得被控对象横摆角加速度方程：

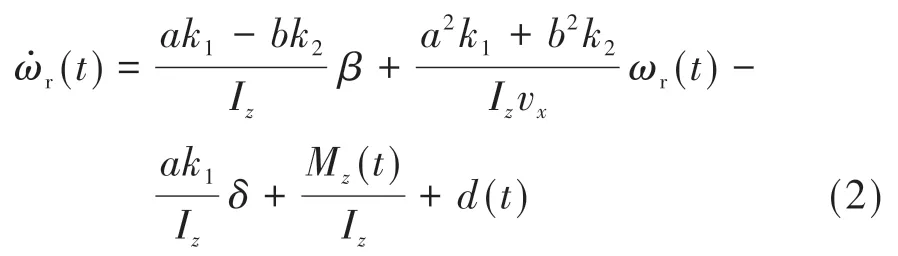
式中()为干扰，且|()|≤，为未加控制时测量得到的干扰上限。

滑模函数为

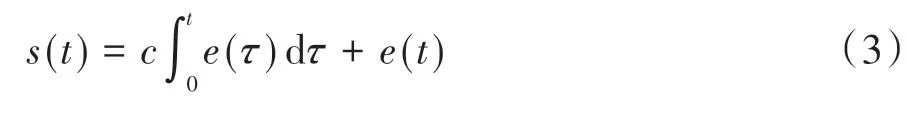
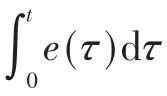
选取跟踪误差为

式中：为高速车辆实际横摆角速度；为高速车辆理想横摆角速度。本文中考虑车辆直线行驶状况车辆侧风控制问题，选取车辆理想横摆角速度=0，前轮转角=0。

对式（3）求导后可得

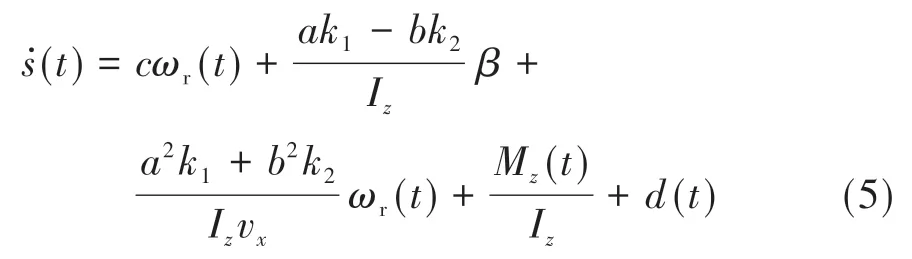
滑模控制器设计为

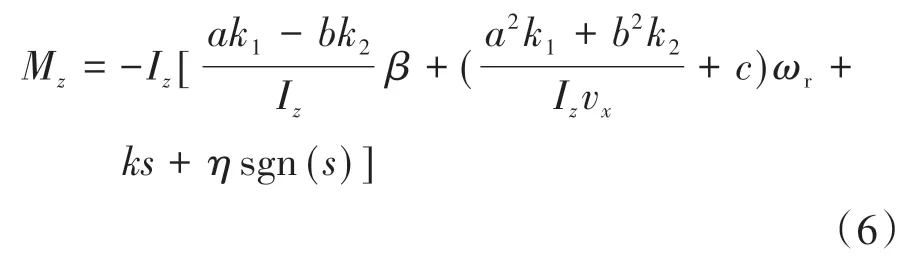
式中＞0，由于高速车辆侧风稳定性控制是具有大阶跃的响应控制，能保证当较大时，系统状态能以较大速度趋近滑动模态。

取Lyapunov函数为

则

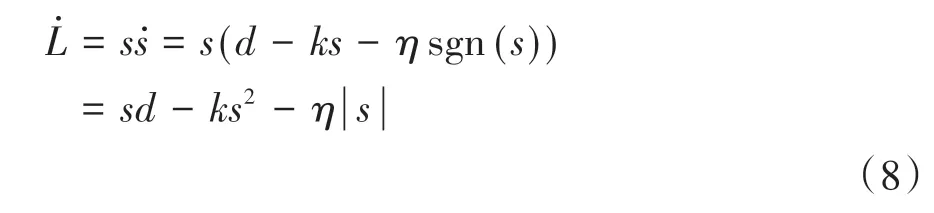
取≥，=+，＞0，则

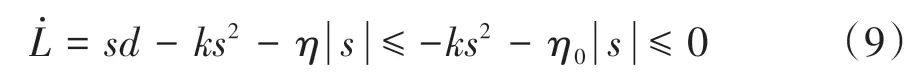
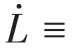
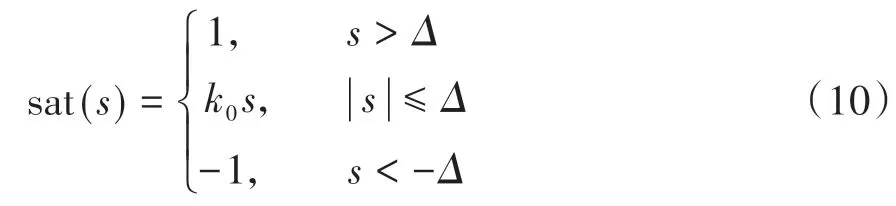
式中：为滑动模态切换面的边界层；=1/。在边界层之内，采用反馈控制，降低滑动模态快速切换的抖振，并使函数sat（）保持在边界层内；在边界层之外，采用切换控制，使系统快速趋近于滑动模态。

4.3 下层控制器

下层控制器按照制动力分配策略，将上层控制器输出的横摆力矩分配到各个车轮，从而完成整个DYC车辆的控制。当对车辆左前轮、左后轮、右前轮及右后轮施加制动力时，会产生制动力F、F、F和F，所引起的横摆力矩分别为

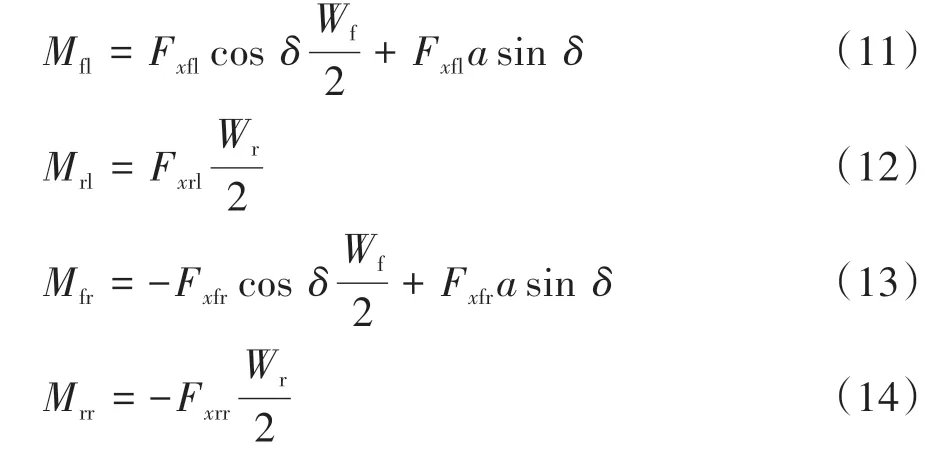
式中：为前轴轮距；为后轴轮距。

DYC 系统的控制方案有单轮控制和双轮控制。单轮控制精度高，对车辆冲击较小，舒适度更好；双轮控制所能产生的横摆力矩比单轮控制大，在紧急情况下更安全。本文采用单轮制动控制为主，双轮制动控制为辅的DYC 下层控制策略。针对高速车辆侧风下直线行驶工况，DYC 系统下层控制策略如表2所示。T、T、T、T分别为左前轮、左后轮、右前轮、右后轮的制动力矩，若车辆需求为左横摆力矩，优先让左前轮制动提供横摆力矩，当T＞800 N·m 时，控制左前轮制动力矩为800 N·m，增加左后轮的制动力矩继续提供横摆力矩，控制左后轮最大制动力矩为600 N·m。若车辆需求为右横摆力矩，优先让右后轮制动提供横摆力矩，当T＞600 N·m 时，控制右后轮制动力矩为600 N·m，增加右前轮的制动力矩继续提供横摆力矩，控制右前轮最大制动力矩为800 N·m。

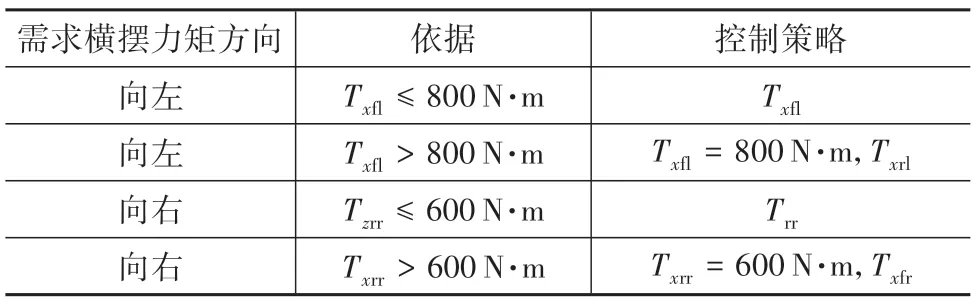
表2 DYC下层控制策略

4.4 控制效果分析

一般认为车速超过100 km/h，为高速行驶状态，且高速车辆与低速车辆相比，对侧风更加敏感，故本文研究的乘用车速度为30 m/s（108 km/h）。转向盘转角为0，车辆保持直线行驶状态，阶跃侧风作用时间为2 s，侧风最大风速取16 m/s。侧风表达式如式（15）所示，仿真结果如图10所示。

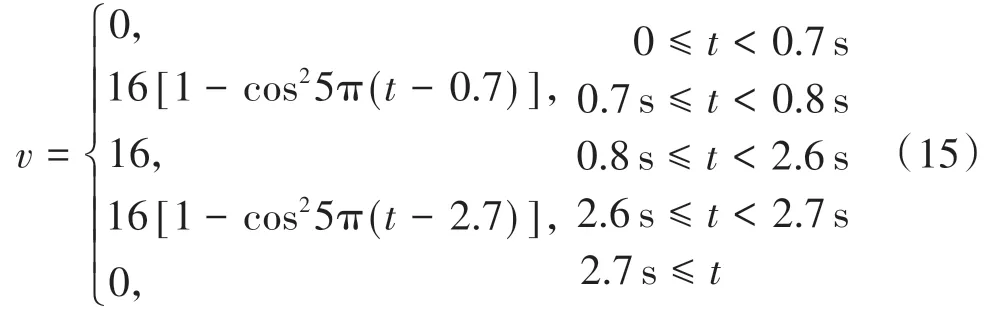
由图10（a）可知：在整个侧风过程中，DYC 车辆的横摆角基本为0，而未受控制车辆的横摆角最大可达-5.7°。在该侧风稳定控制系统下，高速车辆的横摆角可以得到有效控制。

由图10（b）可知：DYC 车辆在该阶跃侧风发生后0.26 s开始，侧风稳定性系统开始参与控制，其横摆角速度与未受控制车辆产生明显区别。在该侧风稳定控制系统的控制下，DYC 车辆的横摆角速度在实际控制中出现了较小的抖振，抖振幅度较小。在整个侧风过程中，未受控制车辆产生较大横摆角速度，最大可达3.5（°）/s，而DYC 车辆最大横摆角速度为1.9（°）/s，减少46%。

由图10（c）和图10（d）可知：在整个侧风过程中，未受控制车辆产生了较大的侧向位移和侧向速度，最大分别可达4.0 m 和2.5 m/s，而DYC 车辆最大侧向位移和侧向速度分别为0.41 m 和0.23 m/s，相对未受控制车辆分别改善89.7%和90.8%。在侧风结束后，未受控制车辆仍然存在较大的侧向速度，侧向位移在不断增加，而DYC 车辆侧向位移保持稳定。

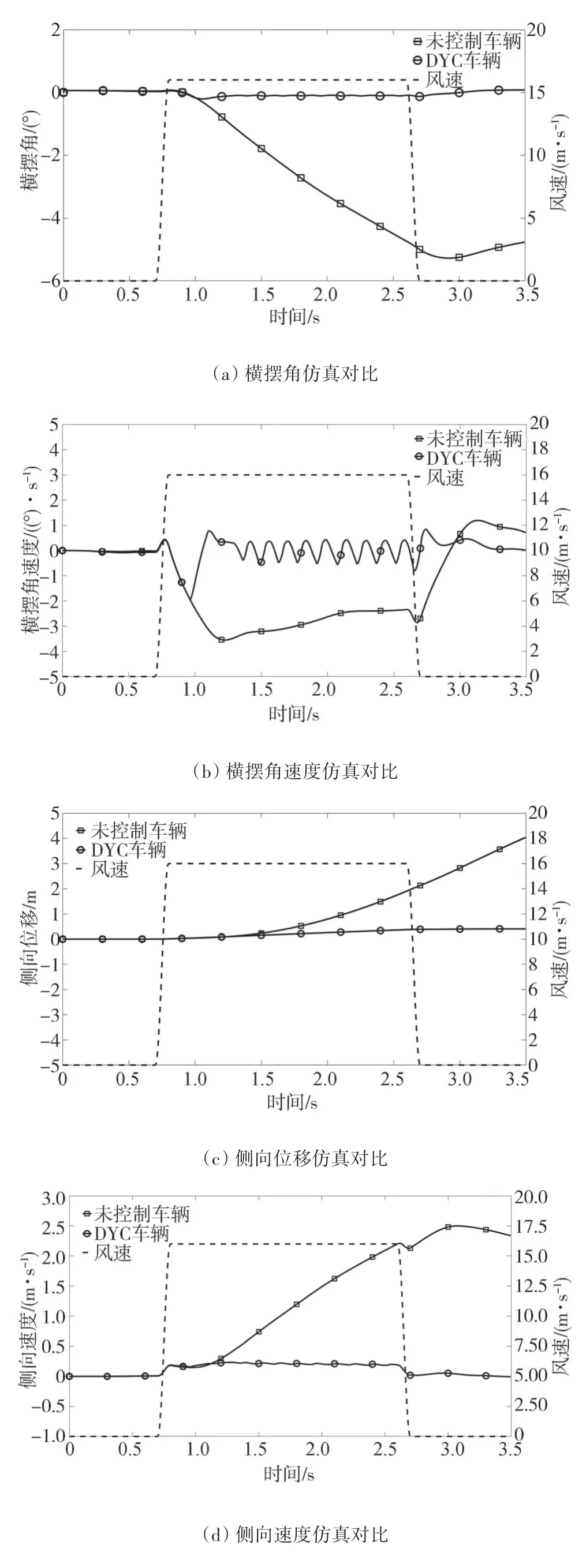
图10 侧风作用下车辆直线行驶仿真结果

4.5 流场分析

通过CFD-MBD 双向耦合控制平台对高速车辆进行侧风稳定性控制分析，可以捕捉到车辆不同行驶状态下的气动力和力矩变化以及不同时刻车身周围流场的瞬态特性，如图11和图12所示。

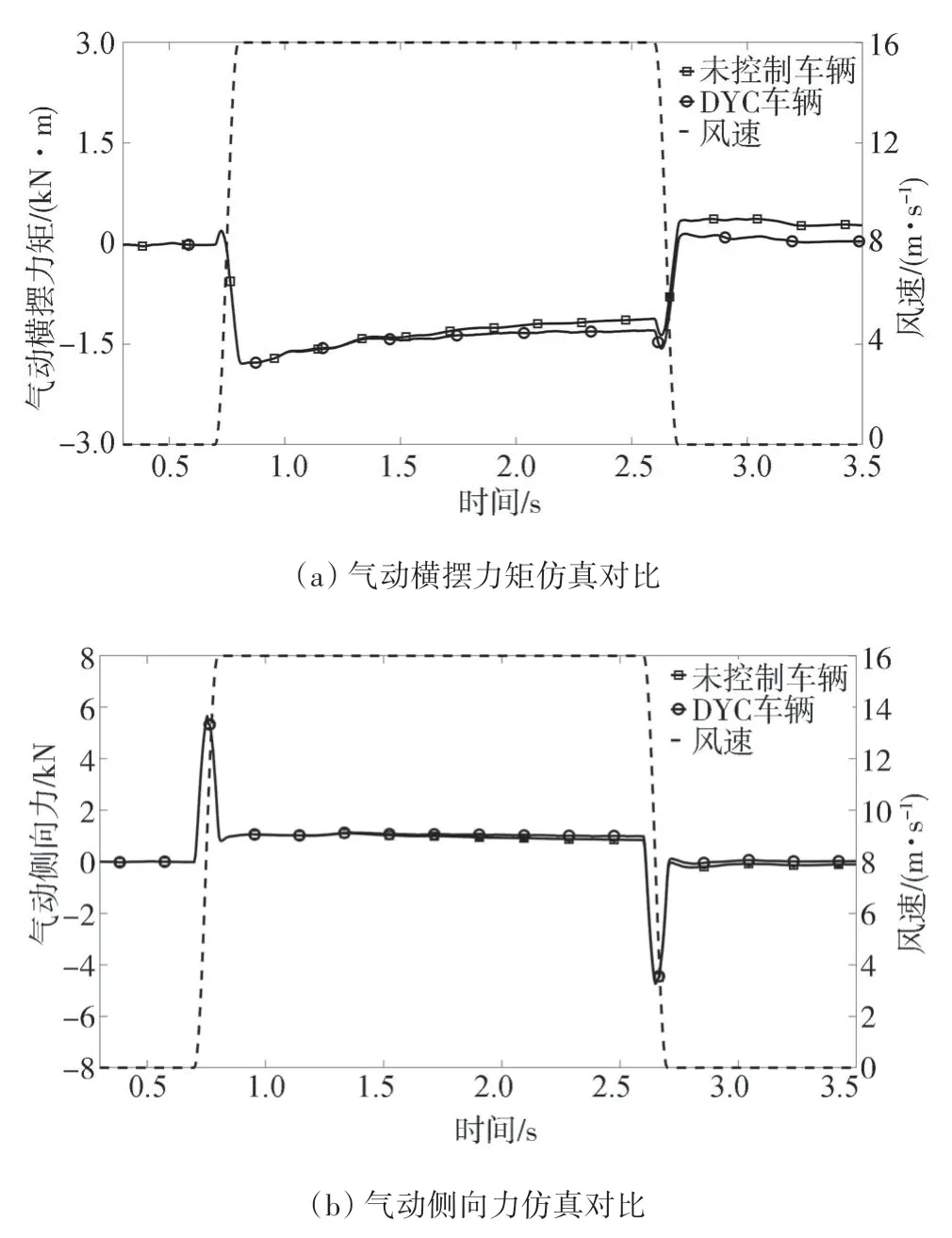
图11 侧风作用下车辆气动力和力矩仿真结果

由图11（a）可知：在阶跃侧风作用的2 s内，DYC车辆相对未受控制车辆产生较大的气动横摆力矩，这是由于DYC 车辆在整个侧风过程中产生的横摆角较小，侧风作用面较大所致。阶跃侧风消失后，未受控制车辆仍具有较小反向气动横摆力矩，这是由于未受控制车辆在侧风消失后仍然存在较小的侧向速度和横摆角所致。

由图11（b）可知：0.7 s后，侧风风速急剧增大到16 m/s，车辆迎风侧压力明显高于背风侧，车辆气动侧向力出现峰值。经2.6 s后，侧风风速急剧减小到0，车辆气动侧向力出现反向峰值。这是由于侧风的突然消失，迎风侧风速急剧减少，背风处风速依然较高所导致。

由图12 可知：当2.2 s 时，车辆处于阶跃侧风中，车辆迎风侧的C 柱和背风处的A 柱产生负压区，车头左侧压力集中，且DYC 车辆迎风侧压力比未控制车辆略大。当=3 s 时，侧风消失，DYC 车辆车身表面压力分布基本对称，未受控制车辆车身表面右侧压力较大，这导致未受控制车辆在侧风消失后会产生较小的反向横摆力矩。

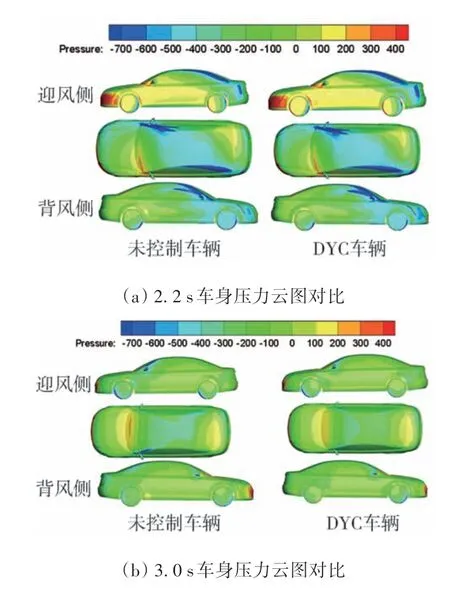
图12 未受控制车辆与DYC车辆车身压力云图

5 结论

针对高速车辆侧风稳定性问题，本文中建立了CFD-MBD双向耦合控制平台，设计了一种基于滑模理论的侧风稳定性控制系统，通过对阶跃侧风下高速车辆的双向耦合控制分析，得到如下结论。

（1）在阶跃侧风中，DYC 车辆横摆角基本为0，未受控制车辆的横摆角最大可达5.7°。在此侧风稳定控制系统下，高速车辆的横摆角能得到有效控制。在阶跃侧风发生后，DYC 车辆横摆角速度出现较小抖振，但抖振幅度较小。DYC 车辆相对未受控制车辆在整个侧风过程中最大横摆角速度减小46%。

（2）在阶跃侧风中，DYC车辆的最大侧向位移为0.41 m，未受控制车辆的最大侧向位移为4.0 m。在此侧风稳定控制系统下，高速车辆的侧向位移得到了有效控制。

（3）通过CFD-MBD 双向耦合控制平台，可以捕捉到车辆不同行驶状态下的气动力与力矩变化，以及不同时刻车身周围流场的瞬态特性。在阶跃侧风作用2 s时间内，DYC车辆相对未受控制车辆产生较大气动横摆力矩。阶跃侧风消失后，未受控制车辆仍具有较小反向气动横摆力矩。在侧风风速快速增加到16 m/s 时，DYC 车辆和未受控制车辆的气动侧向力都出现峰值，侧风风速快速减小到0 时，DYC 车辆和未受控制车辆气动侧向力都出现反向峰值。