基于模糊LQR的智能汽车路径跟踪控制*

胡 杰，钟鑫凯，陈瑞楠，朱令磊，徐文才，张敏超

（1.武汉理工大学，现代汽车零部件技术湖北省重点实验室，武汉 430070；2.武汉理工大学，汽车零部件技术湖北省协同创新中心，武汉 430070；3.新能源与智能网联车湖北工程技术研究中心，武汉 430070）

前言

近年来，智能汽车发展迅速，在一些封闭场景中已实现商业化落地，具有广阔的前景。智能汽车的路径跟踪控制是实现自动驾驶的关键技术之一，其主要功能是控制车辆的前轮转角，使车辆能够沿参考路径行驶，尽可能地减少受控车辆与参考路径之间的偏差。在非极限工况下，跟踪精度是路径跟踪控制的首要目标。

国内外研究人员针对智能汽车的路径跟踪控制问题进行了大量研究工作。现有的路径跟踪控制方法，可根据是否采用车辆模型分为两类。无模型控制方法不需要建立车辆模型，忽略车辆特性，直接根据车辆与参考路径之间的偏差计算前轮转角，包括PID 控制方法和模糊控制方法等；基于模型的控制方法需要建立车辆运动学或动力学模型，充分考虑车辆的系统特性，包含纯追踪控制方法、Stanley 控制方法、MPC 控制方法和LQR 控制方法等。

上述路径跟踪控制方法中，LQR 控制方法能够兼顾多项性能指标，在中低车速工况下具有较好的控制效果；并且具有较好的实时性，对硬件设备要求低，能够满足工程实践的需要。因此，许多研究人员对LQR 路径跟踪控制方法开展了深入研究。文献［11］中基于LQR 提出了前轮转角与横摆力矩的集成控制策略，该策略具有较好的跟踪精度与横向稳定性。为了减小LQR 控制器的稳态误差，文献［12］和文献［13］中构建了加入前馈控制的LQR 控制器，相较于未带前馈控制的LQR 控制器，有效减少了跟踪误差。更进一步，文献［14］中针对LQR 控制器权重固定的问题，提出了基于跟踪偏差的权重调整策略，再次提升了LQR 控制器的精确性。

虽然加入前馈控制对LQR 控制器进行转角补偿，可以在一定程度上提高跟踪精度，但前馈控制和LQR 控制器都是基于同一简化系统模型，存在较大的局限性。实际车辆是一个复杂系统，前馈控制不能有效减少由于系统参数不确定性所导致的跟踪误差。同时，系统以质心为控制点，前馈控制相对滞后，可能产生超调，导致车辆转角频繁变动，行驶稳定性变差。此外，不同的车速条件下，同一控制转角引起的车辆位置变动不同。因此，即使路径偏差相同，也需要控制器根据车速变化输出相应控制转角。由于简化建模、系统参数不确定以及执行机构响应滞后等问题，LQR 控制器自身并不能很好地适应车速变化，固定的权重参数无法保证不同车速下控制效果。

针对上述问题，本文中设计了一种带预瞄PID的模糊LQR 路径跟踪控制器。首先建立了路径跟踪误差模型，在此基础上设计了LQR 控制器，并采用预瞄PID 的方法对LQR 控制器进行转角补偿，减小稳态误差；然后分析车速变化对于控制效果的影响，提出了基于车速的权重参数模糊调节策略，对权重参数进行自适应调节，以此保证不同车速下的控制效果；最后，通过实车试验平台对设计的控制器进行对比分析，验证其准确有效。

1 路径跟踪误差模型

1.1 车辆动力学模型

智能汽车的路径跟踪控制，主要涉及车辆的侧向运动与横摆运动，为简化计算，假设车辆同轴车轮具有相同的侧偏刚度与转角，由此可以合并同轴车轮，采用2 自由度单轨车辆模型作为车辆模型，如图1所示。

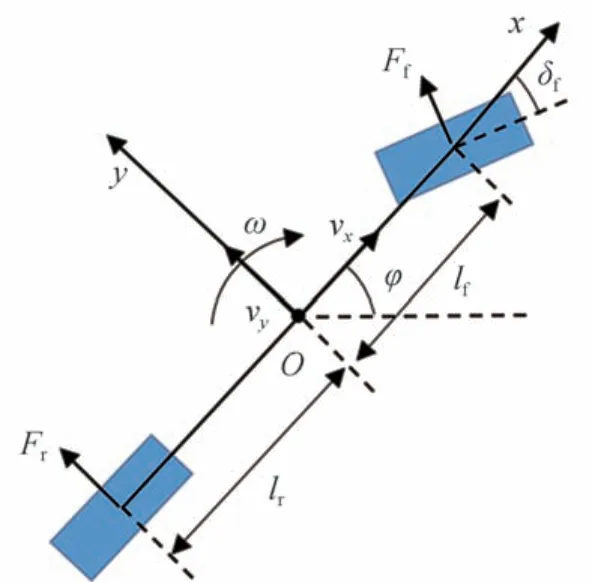
图1 车辆动力学模型

假设车辆匀速行驶，且前轮转角较小，分析车辆受力情况，可以得到：

式中：为整车质量；a为车辆的侧向加速度；F、F分别为车辆的前、后轮胎所受侧向力；I为车辆绕垂线方向的转动惯量；为车辆的横摆角速度；、分别为车辆前、后轴与质心的距离。

在附着条件良好、车速较低的常规工况下，车辆的轮胎侧偏角较小，可认为轮胎所受侧向力与侧偏角成线性关系。由此，得到车辆动力学模型：

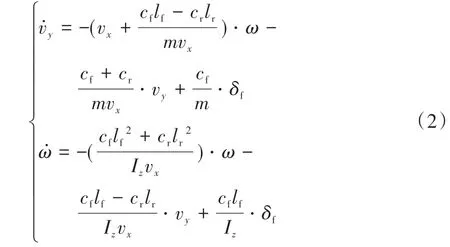
式中：v、v分别为车辆的纵、横向车速；、分别为车辆前、后轴车轮的侧偏刚度；为前轮转角。

1.2 路径跟踪误差模型

智能汽车跟踪参考路径时，主要考虑侧向误差和航向误差。如图2 所示，定义车辆质心到参考路径的最短距离为侧向误差e，车辆航向角与参考航向角之差为航向误差e。

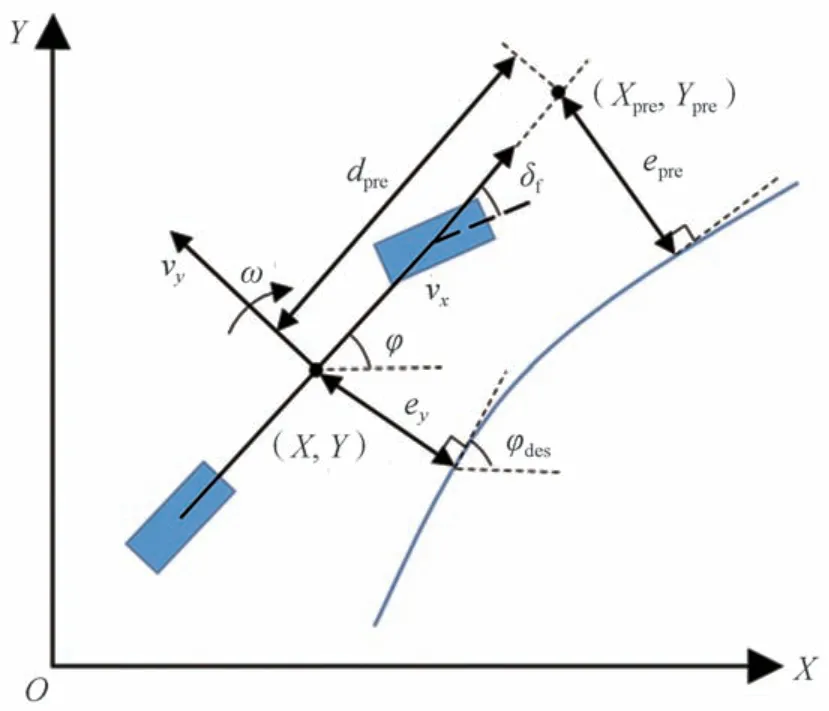
图2 路径跟踪误差模型

假设航向误差较小，可以得到航向误差和侧向速度误差：

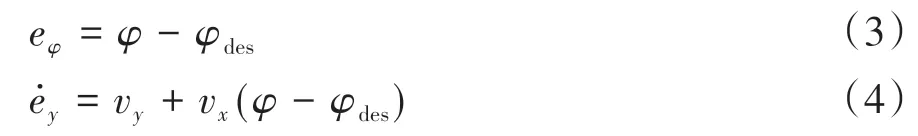
式中：为车辆当前航向角；为参考航向角。

假设参考路径的转弯半径为，可以得到车辆的参考侧向加速度为

车辆的实际加速度为

根据式（5）和式（6），可以得到侧向加速度误差为

综合上述内容，可以得到

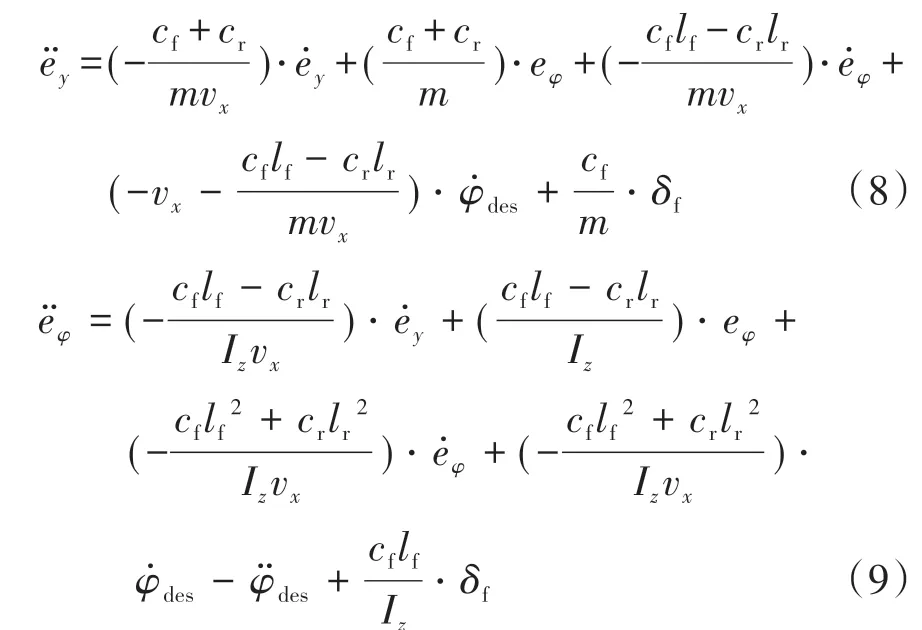
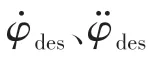
其中：

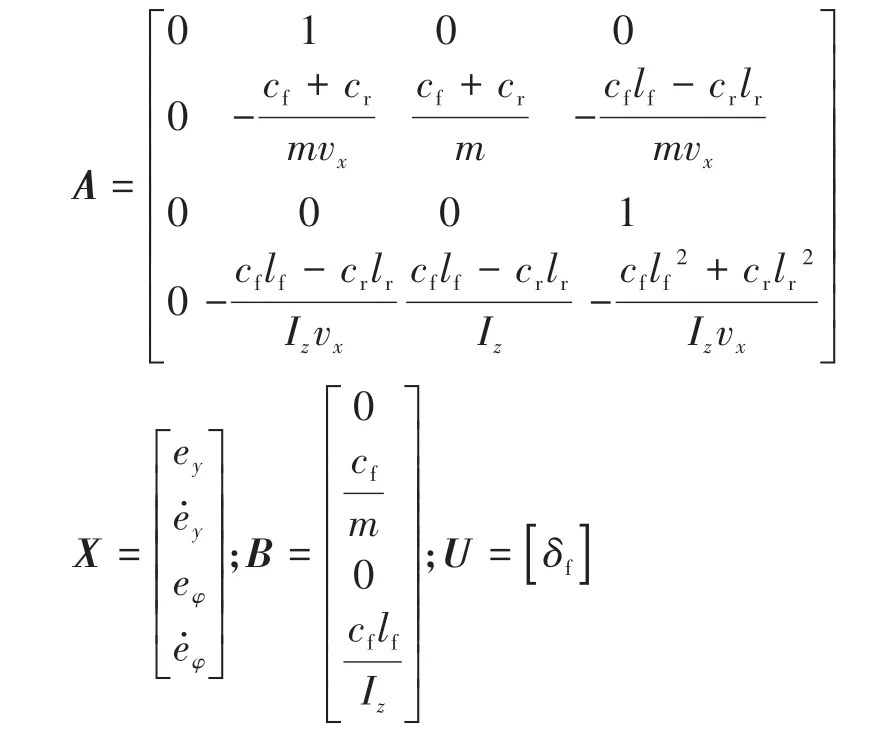
2 路径跟踪控制器

路径跟踪控制器的整体结构如图3 所示。首先基于路径跟踪误差模型，设计LQR 控制器作为路径跟踪控制器的主体部分，使车辆基本按照参考路径行驶；在此基础上，采用预瞄PID 方法作为转角补偿，消除由于系统简化与参数失准导致的稳态误差，同时避免由于响应滞后而产生的超调；最后，对LQR控制器的权重参数进行模糊调节，提升控制器对于车速的适应性。

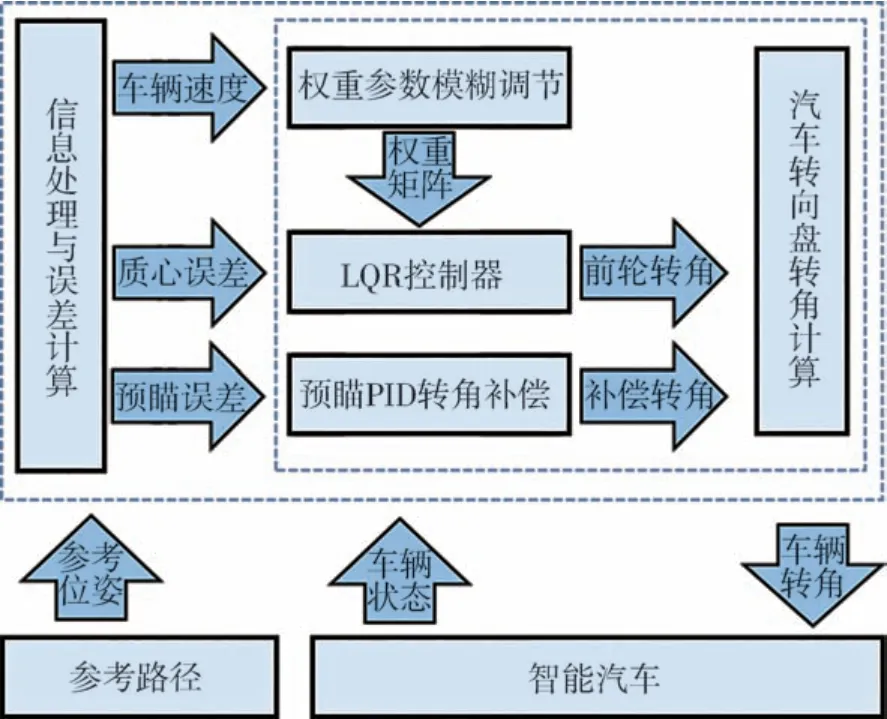
图3 路径跟踪控制器结构

2.1 LQR控制器

LQR 控制器针对离散系统进行控制，因此设定控制步长为，选择双线性离散化的方法，将连续的状态空间方程转换为离散系统，可以得到：

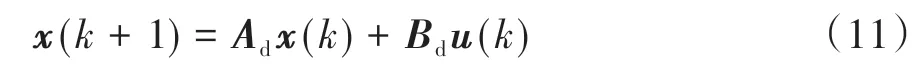
式中：=(-/2)(+/2)；=；()为时刻的状态量；()为时刻的控制量。

LQR控制器的控制目的不仅需要减小车辆的路径跟踪误差，还需要保持控制量尽可能小，以保证车辆行驶的稳定性。由此，定义如下目标函数：

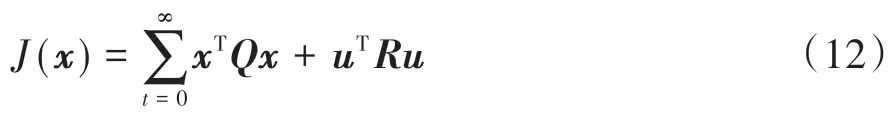
式中：为状态量；为控制量；为状态量权重矩阵；为控制量权重矩阵。

假设LQR控制器的控制律为

式中为控制增益系数。

将式（13）代入式（12），可以得到：

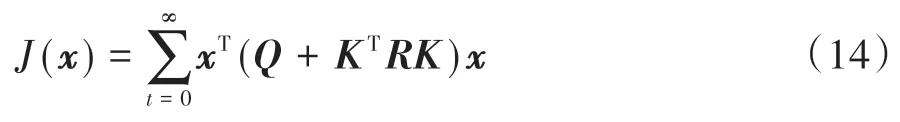
假设存在一常量矩阵，使系统趋于稳定，可以得到：

式中为如下Riccati方程的正定解：

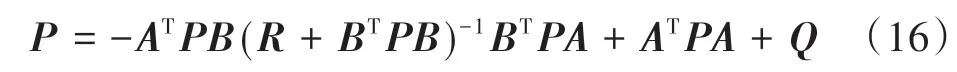
2.2 预瞄PID转角补偿

预瞄PID 控制方法不依赖于系统建模，直接针对误差进行控制，在小范围内具有良好的稳定性，采用此方法进行小角度的转角补偿，能够有效弥补由于系统简化和参数失准导致的稳态误差。此外，由于加入了预瞄距离，控制器存在一定预见性，可以有效改善转向滞后问题，避免超调。

如图2 所示，智能汽车的预瞄距离为，其数值大小与车速相关，具体如下：

式中：为基础预瞄距离；为预瞄时长。

由此，可以确定预瞄点位置：

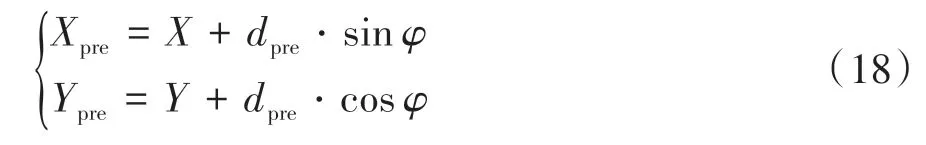
式中：、为智能汽车质心的纵、横向位置；、为预瞄点纵、横向位置；为车辆航向角。

定义预瞄点与参考路径之间的最短距离为预瞄误差，预瞄PID 控制器直接针对离散系统的误差进行控制，控制步长与LQR 控制器保持一致，具体如下：

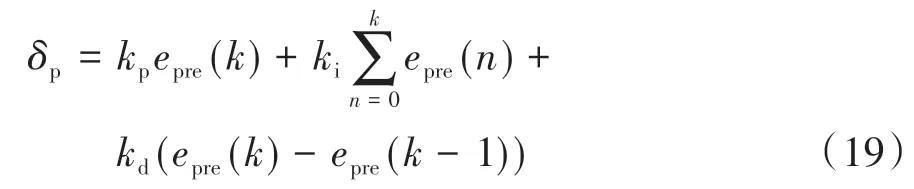
式中：为预瞄PID 控制器输出的补偿转角；、、分别为比例、积分、微分常数；()为时刻的预瞄偏差。

综合上述内容，可以得到控制系统最终输出至智能汽车的转向盘转角为

式中表示车辆转向机构的传动比。

2.3 权重参数模糊调节

实车环境中，系统复杂，与理想条件差别较大，车速变化会对路径跟踪控制器的控制效果造成较大影响。固定权重的控制器无法较好地适应车速变化，在不同车速条件下保持良好的控制效果。针对此问题，本文中采用模糊控制方法实现对LQR 控制器权重参数的自适应调节，保证不同车速条件下的跟踪性能。

2.3.1 变量设计

LQR 控制器包含两个权重矩阵和，分别对应状态量与控制量，可以描述为

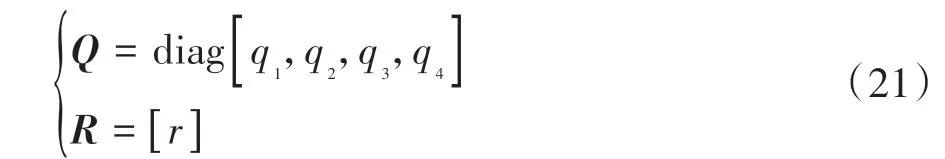
式中：、、、分别为侧向误差、侧向速度误差、航向误差、航向角速度误差的权重参数；为前轮转角的权重参数。

智能汽车跟踪参考路径时，控制器主要针对侧向误差、航向误差和前轮转角3 个变量进行控制，兼顾准确性与稳定性。权重参数越大，其对相应变量的限制作用越强，权重参数的相对大小决定了控制器对各变量的控制程度。误差的权重参数越大，跟踪精度越高；转角的权重参数越大，转角变化越小，驾驶的稳定性与舒适性更好。在低车速条件下，车辆行驶平稳，应增大误差权重，以保障跟踪精度为主。在高车速条件下，车辆短时间的位置变动较大，转角过大容易导致超调，所以应增大转角权重，加强对前轮转角的限制，防止车辆因超调而左右摇摆，导致车辆的跟踪精度与行驶稳定性变差。

根据上述分析，本文中将、置为0，同时设定为固定值，通过调节和，改变权重的相对大小，实现控制器对于车速变化的自适应。设定模糊调节的输入变量为车速v，输出变量为控制系数、的调整量，表示为Δ、Δ。各变量取值范围如表1所示。

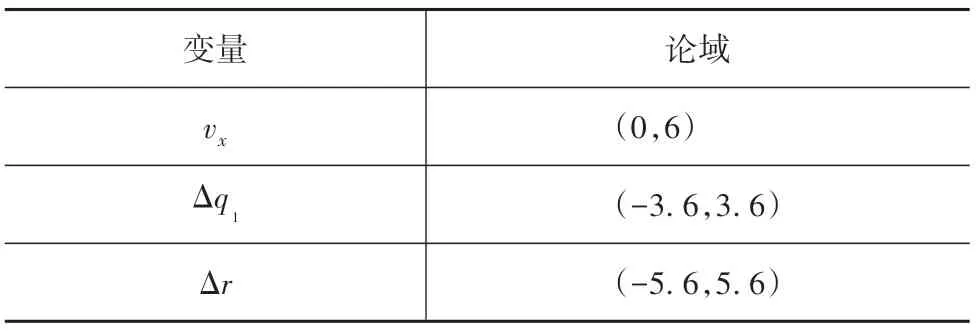
表1 变量论域

2.3.2 模糊化处理

模糊语言变量集划分为5 个模糊子集：负大（NB），负小（NS），零（O），正小（PS），正大（PB）。隶属度函数为高斯型函数，具体如下：

式中：为变量；和为参数。

分别对输入与输出变量进行模糊化处理，结果如图4所示。

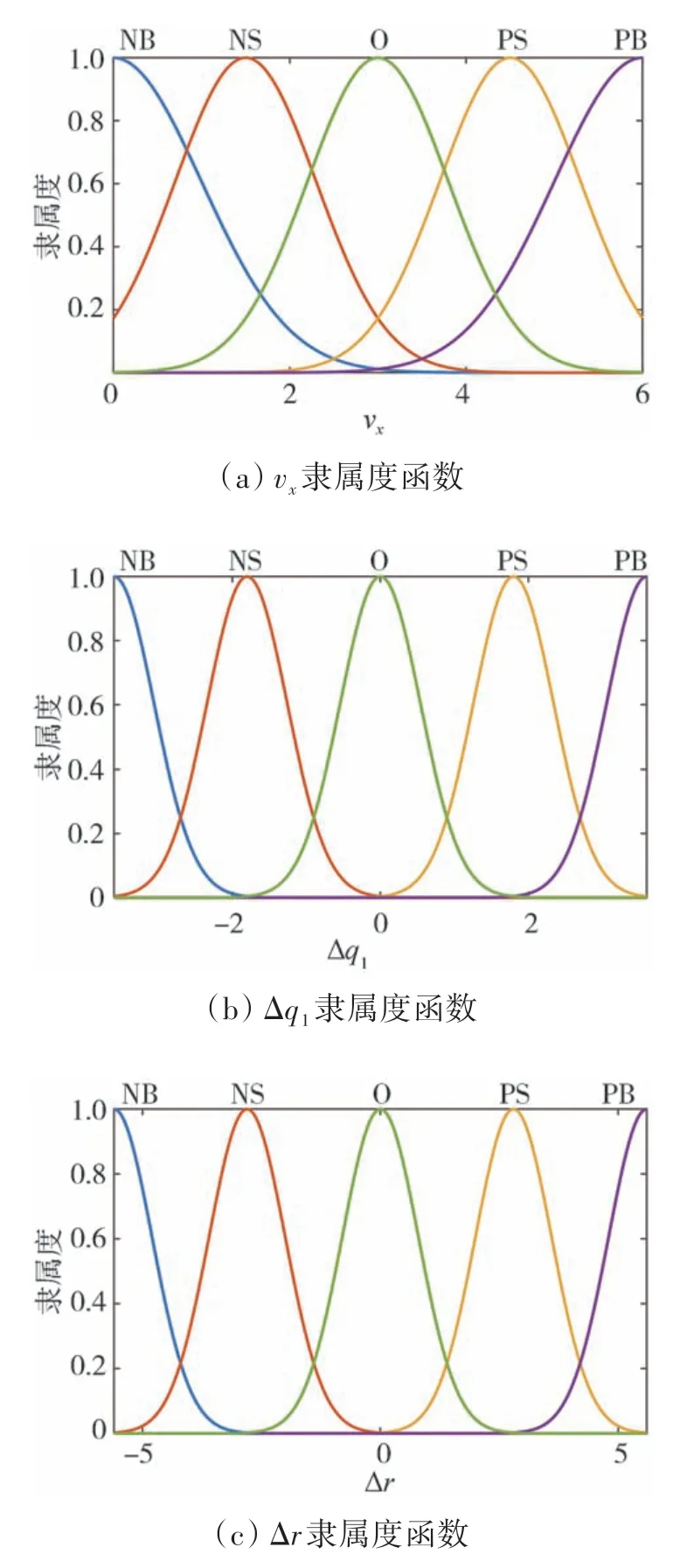
图4 隶属度函数

2.3.3 模糊规则与解模糊

智能汽车的车速越高，对前轮转角的限制程度应越大，保持行驶稳定，防止超调振荡，具体模糊规则如表2所示。

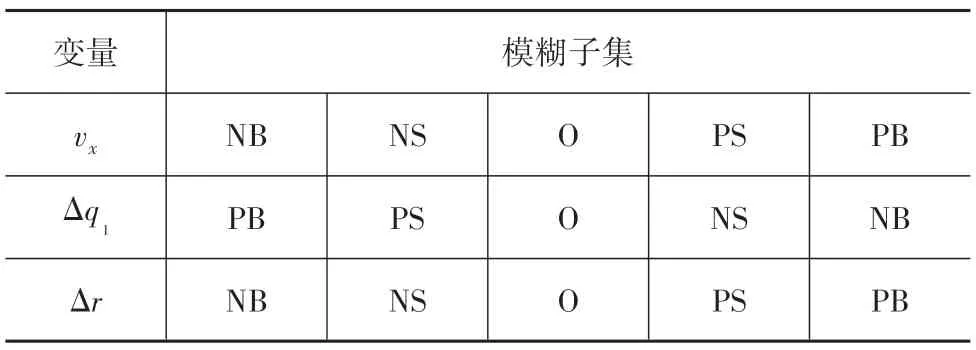
表2 模糊规则

根据制定的模糊规则，输入量经模糊推理后，可得到模糊输出量，选择质心法解模糊，得到精确输出量Δ、Δ。

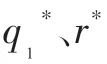
式中、分别为基准车速下侧向误差、前轮转角的最优权重参数。

最后，得到不同车速下的最优权重矩阵：

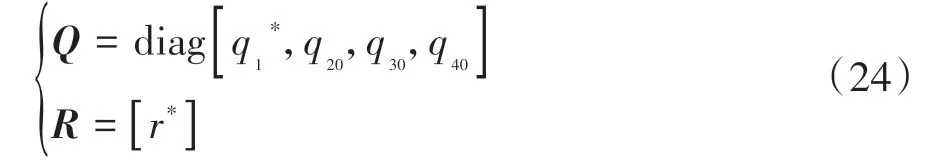
式中、、分别为基准车速下侧向速度误差、航向误差和航向角速度误差的最优权重参数。

3 实车试验

为验证设计的路径跟踪控制器，基于实车试验平台对其进行试验测试。

所用的实车试验平台由纯电动线控乘用车底盘改装而来，加装了摄像头、毫米波雷达、激光雷达、GPS、IMU等高性能传感器，如图5（a）所示。

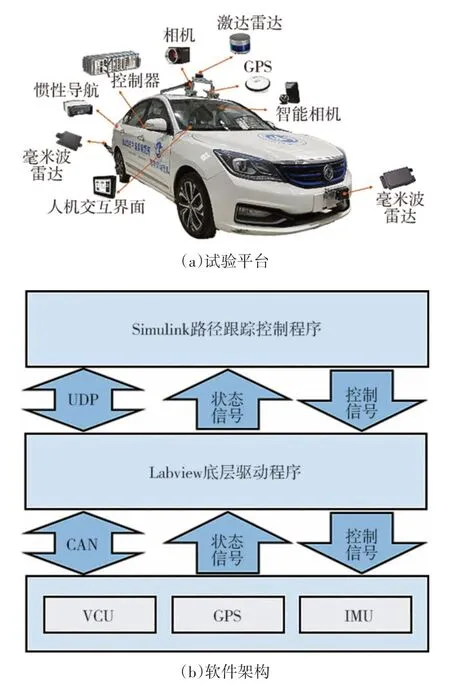
图5 实车试验平台与软件架构

整车的结构参数如表3所示。

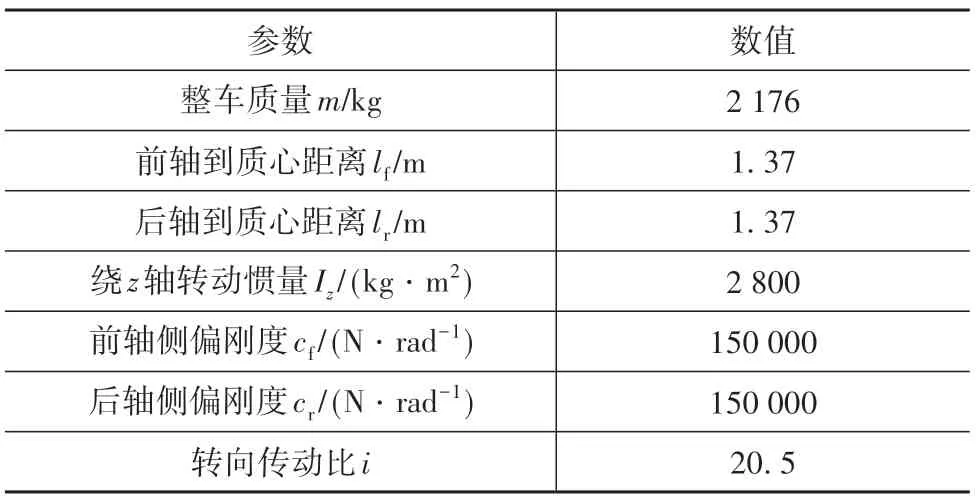
表3 整车结构参数

实车试验平台的软件架构如图5（b）所示，为便于实时调整，采用分层控制结构。上层路径跟踪控制程序采用Simulink 编写，部署在PC 上，通过UDP与底层驱动程序通信；GPS、IMU、车辆VCU 控制等模块的驱动程序采用LabVIEW 编写，部署在NI控制器中，通过CAN 报文与硬件设备进行通信，实时接收传感器信号并控制车辆。

试验场地为校园内一封闭练车场，采用Fishhook 型路径。车辆转角由路径跟踪器控制，车速采用PID控制，控制频率均为50 Hz。

3.1 转角补偿效果试验

为进行对比分析，分别设计了无转角补偿的LQR 控制器和带前馈控制的LQR 控制器，与本文中设计的控制器同时进行路径跟踪试验。车速设定为3 m/s，LQR 控制权重均为当前车速下的最优权重参数。试验结果如图6～图8所示。

图6显示了在3种控制器作用下，车辆的实际行驶路径与参考路径的对比。可以看出，带预瞄PID的LQR 控制器对于参考路径的跟踪效果最好，而无转角补偿的LQR 控制和带前馈控制的LQR 控制器均存在较大的稳态误差，其中无转角补偿的LQR 控制器稳态误差最大，与参考路径出现了明显的偏离，跟踪效果最差。

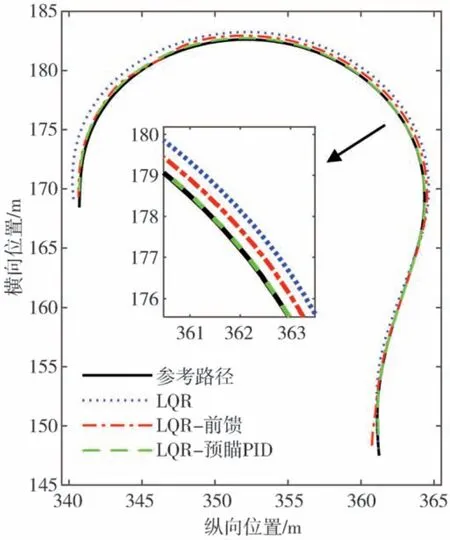
图6 不同转角补偿下的路径跟踪结果

图7（a）和图7（b）精确描述了车辆与参考路径的侧向偏差与航向偏差。可以看出，车辆贴近参考路径稳定行驶后，带预瞄PID 的LQR 控制器的跟踪精度最高，最大侧向偏差在0.14 m 以内，最大航向偏差在1.35°以内；无转角补偿的LQR 控制器跟踪精度最差，最大侧向偏差达到0.71 m，最大航向偏差在3.6°左右；带前馈控制的LQR 控制器虽然最大侧向偏差为0.38 m，但最大航向偏差达到9.25°，并且车辆航向角出现了高达16°的摆动幅度，转角在短时间内变动过大，车辆行驶的稳定性较差。

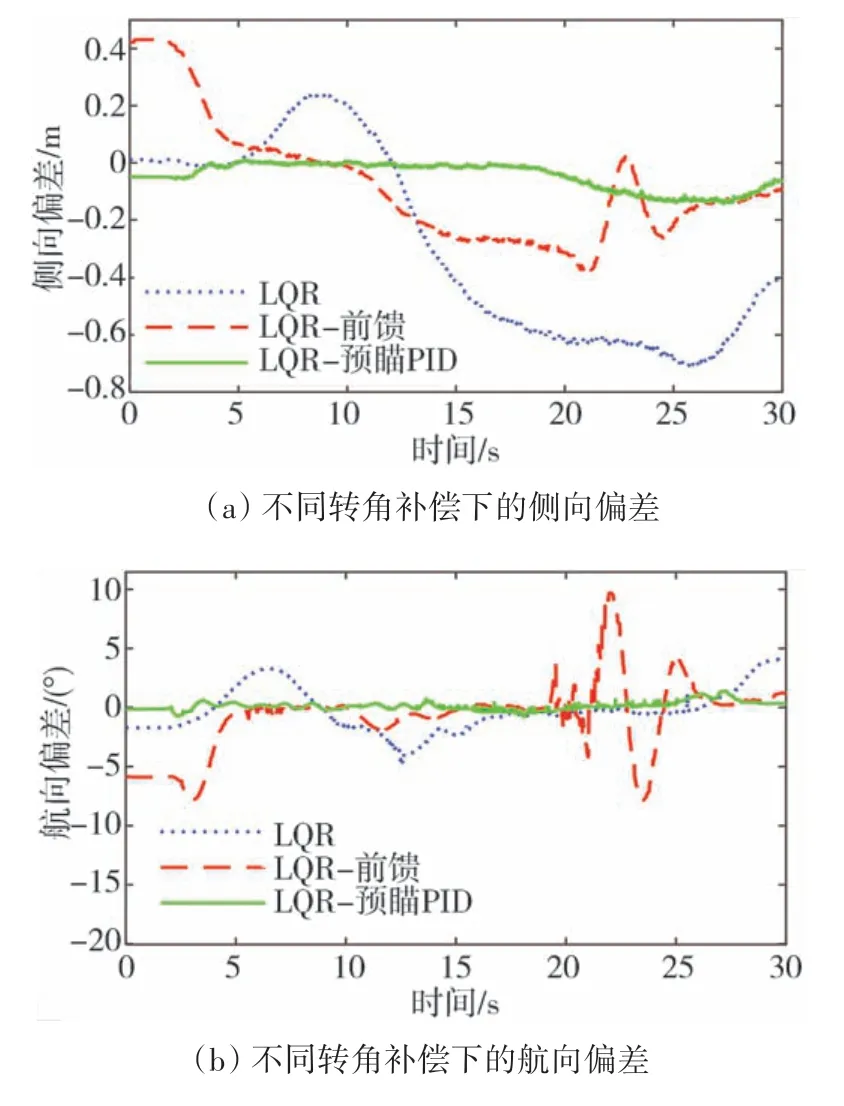
图7 不同转角补偿下的跟踪误差

图8 描述了3 种控制器的输出控制转角与车辆实际转角。结合图7和图8可以看出，带有前馈控制的LQR 控制器虽然减小了一定的稳态误差，但是由于前馈控制是以车辆质心为基准点，控制存在一定的滞后，当存在外界扰动或曲率增加，导致误差增大时，转向盘转角出现较大幅度的调整，出现超调问题。由图8（a）可以看出，带有前馈控制的LQR 控制器的最大输出转角大达到500°左右，并且变动迅速，而车辆的实际转角存在一定的响应滞后，从而导致车辆不能及时调整，进一步加剧了超调问题，使得车辆航向角发生较大变动，出现左右摆动的现象。

由图8（b）和图8（c）可以看出，无转角补偿的LQR 控制器和带预瞄PID 的LQR 控制器输出的转向盘转角都比较平滑，没有大幅跳变，车辆的实际转角与之吻合较好，车辆无明显摆动，稳定性较好。

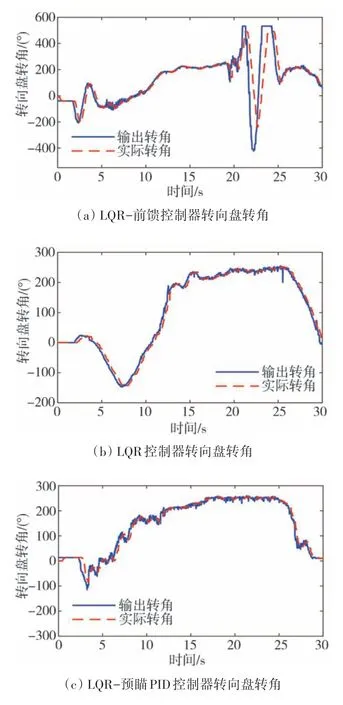
图8 不同转角补偿下的转向盘转角

3.2 权重参数模糊调节效果试验

为试验对LQR 控制器权重参数进行模糊调节的效果，在带预瞄PID 的LQR 控制器的基础上，分别采用固定权重、模糊调节权重两种方法，在不同车速下试验控制器的控制效果。其中，固定权重和模糊调节的基础权重参数均采用车速为3 m/s 时的最优控制权重，试验车速为1.5 和4.5 m/s。试验结果如图9～图13所示。

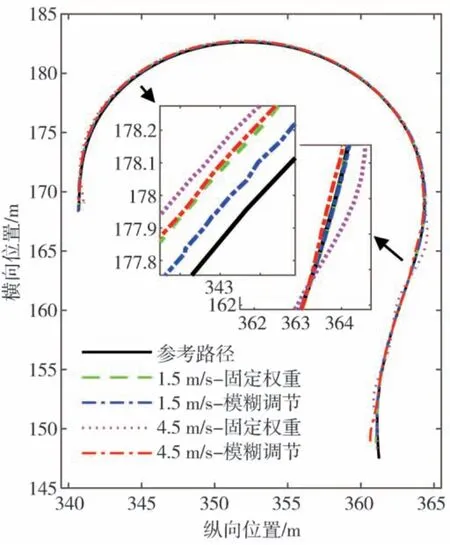
图9 不同车速下的路径跟踪结果

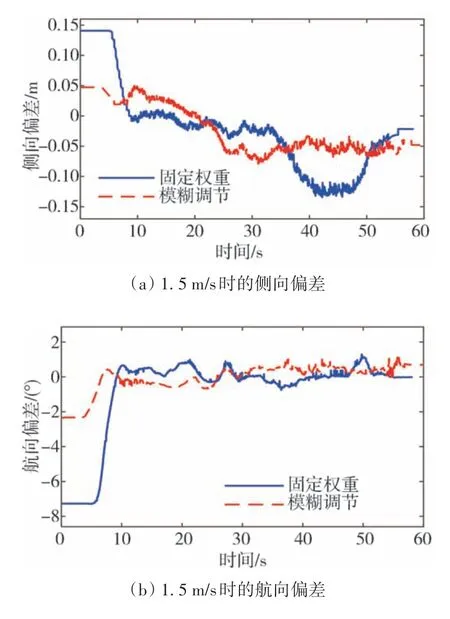
图10 1.5 m/s时的跟踪误差

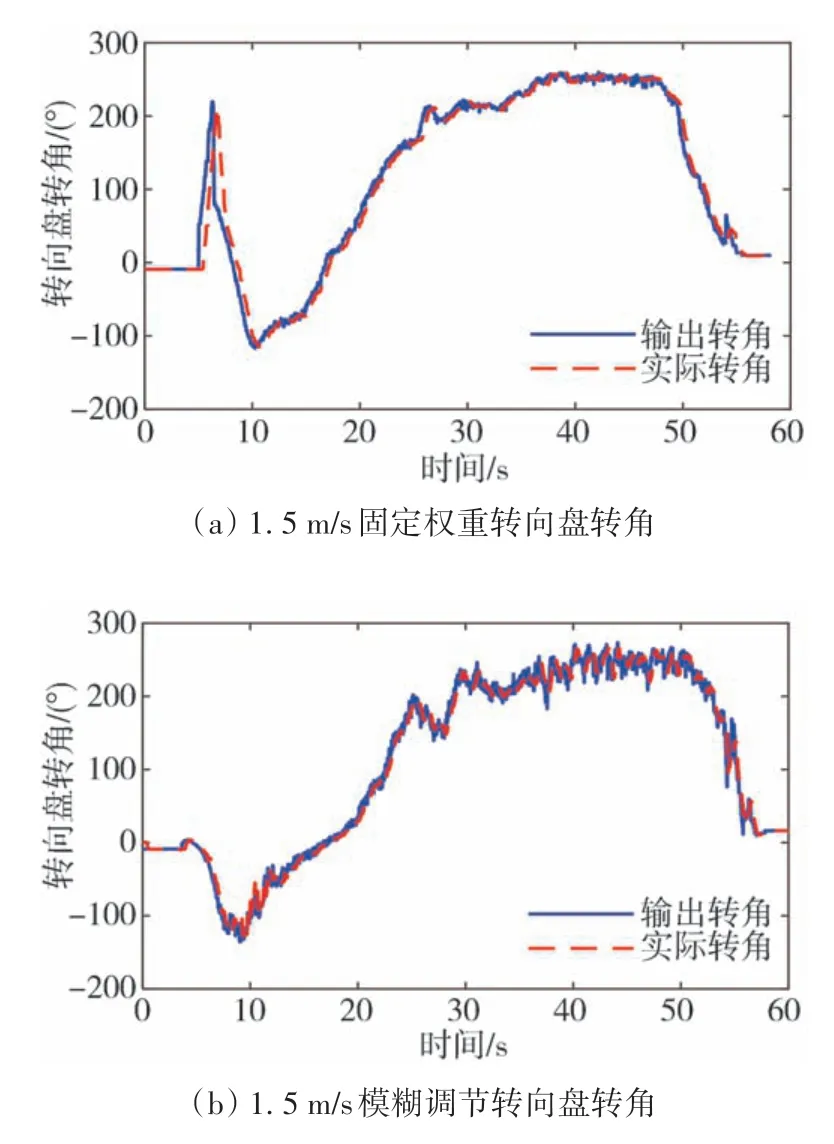
图11 1.5 m/s时的转向盘转角

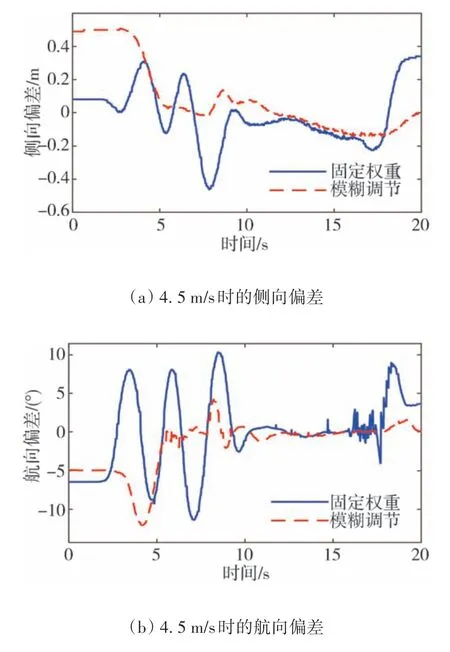
图12 4.5 m/s时的跟踪误差

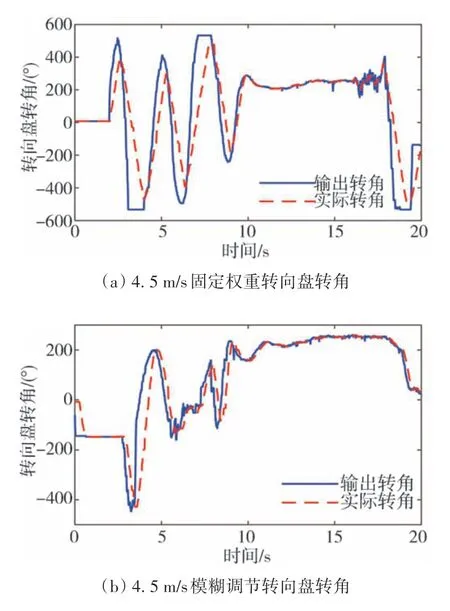
图13 4.5 m/s时的转向盘转角

图9 显示了车辆在不同车速、不同控制器作用下，实际行驶路径和参考路径的对比。可以看出，在两种车速条件下，权重参数采用模糊调节的控制器均具有较好的路径跟踪效果，跟踪精度明显优于同车速下的固定权重控制器。此外，在同一控制器作用下，车速为4.5 m/s时的跟踪精度比1.5 m/s时差，尤其是采用固定权重控制器时，4.5 m/s 车速下车辆出现了明显的振荡，转角频繁变化，严重影响到车辆的稳定性。这是由于固定权重控制器没有随着车速提高而相应增加对控制量的限制导致的，较高车速下，即使保持低速时相同的转向盘转角，车辆在控制时域内产生的位置变动也会更大，从而发生超调，产生新的偏差，使得控制器反复调整，转角频繁变动，车辆出现左右摇摆现象。而权重参数采用模糊调节的控制器，其控制量权重随着车速增加而增大，虽然跟踪精度相较于低速时有所降低，但保持了车辆行驶的稳定性。

图10～图13精确地描述了不同车速下两种控制器的跟踪精度与转角变化。

由图10 可以看出，在1.5 m/s 车速下，权重参数采用模糊调节的控制器将侧向偏差保持在0.07 m以内，航向偏差保持在0.8°以内。相较于固定权重控制器，其较好地减小了侧向偏差，实现了更高的跟踪精度。图11 描述了1.5 m/s 车速下，两种控制器的控制转角与车辆实际转角。可以看出，为保证更高的跟踪精度，权重参数采用模糊调节的控制器对于转向盘转角的调节更加精细，在低车速下，这种微小的调节不会引起车辆左右摆动，不会对车辆的稳定性造成影响。

由图12可以看出，在4.5 m/s车速下，固定权重控制器的侧向偏差和航向偏差均出现了大幅度的振荡现象，侧向偏差最大振幅达到0.64 m，航向偏差最大振幅达到19°，且跟踪误差的收敛时间较长，车辆长时间未进入稳定状态，跟踪精度与跟踪稳定性很差。而权重参数采用模糊调节的控制器可以快速收敛跟踪误差，无大幅波动，最大侧向偏差为0.15 m，最大航向偏差在3°左右，路径跟踪的精度与稳定性都比较好。

由图13（a）可以看出，固定权重控制器为了减小跟踪误差，其输出的转向盘转角过大，而车辆的转向机构的响应较为滞后，在车速较高的工况下，这导致车辆与理想位置存在较大偏差，使得控制器对转向盘转角进行反复调节，从而引起振荡，难以收敛。而由图13（b）可以看出，权重参数采用模糊调节的控制器由于针对高速调节了控制器权重，其输出的转向盘转角较小，有效避免了响应滞后与超调现象，不仅保证了车辆行驶的平稳，同时还保证了足够的跟踪精度。

4 结论

本文中设计了一种智能汽车的路径跟踪控制器，采用LQR 控制器作为主体部分，并使用预瞄PID方法进行转角补偿，提高跟踪精度，同时根据车速对LQR 控制器的权重参数进行模糊调节，保证控制器在不同车速下的跟踪效果。实车试验结果表明，该路径跟踪控制器能够有效克服由于系统简化建模和响应滞后引起的误差问题，实现更加精准的路径跟踪控制，且避免了传统前馈补偿的超调现象；同时，控制器在不同车速工况下，均能保持较好的跟踪精度与行驶稳定性，具有较强的适应性。