基于连续弹性基础梁模型的扣件动刚度测试方法

闫子权

（1.高速铁路轨道技术国家重点实验室，北京 100081；2.中国铁道科学研究院集团有限公司 铁道建筑研究所，北京 100081）

轨道扣件系统是钢轨与轨下结构连接的纽带，对保证轨道整体稳定性和可靠性起着重要作用，是铁路基础设施中的关键零部件之一［1］。扣件刚度是轨道结构力学特性的一个重要参数，也是影响列车运行速度、安全性、平稳性以及轨道维修工作量的重要参数［2−3］。

扣件刚度可分为扣件静刚度和扣件动刚度［4］，目前扣件静刚度和低频动刚度的试验方法比较成熟，且有相应的测试标准，如TB/T 3396.3—2015和EN 13146-9—2011 中均规定了扣件组装静刚度的室内测试方法，该方法通过试验机向组装扣件系统的钢轨施加垂直于钢轨底面的荷载，测定钢轨在荷载作用下产生的相对于轨枕的位移进而得到静刚度［5−6］。TB/T 3395.1—2015中规定了扣件弹性垫层低频动刚度的试验方法，该方法通过试验机以恒定频率（4 Hz）对扣件弹性垫层施加垂向循环荷载，测定最大和最小荷载下弹性垫层的最大和最小垂向位移进而得到低频动刚度［7］。

对于扣件高频动刚度及服役状态下的扣件动刚度测试方法，国内外学者开展了大量的研究工作。动刚度取决于弹性元件的弹性、惯性和阻尼特性。由于惯性力的存在，高频动刚度比低频动刚度更为复杂。根据ISO 10846系列标准［8］的相关规定，弹性元件动刚度和阻尼特性的室内测试方法有3 种，分别为直接法、间接法和驱动点法。直接法需要测量输入端的位移和阻滞输出力，比利时布鲁塞尔大学采用直接法测量了扣件弹性垫层的动刚度［9］，但直接法的测试有效频率范围较低，一般小于500 Hz。间接法是用测量振动的传递率来实现，英国南安普顿大学Thompson 等［10−11］根据间接试验方法研究了激励频率和预荷载对弹性垫层动刚度的影响。间接法测试频率较高，最高可达2 000 Hz，但无法有效测得低频处的动态特性。由测量输入端位移和输入力而得出的刚度就是驱动点动刚度，只有在低频段，驱动点刚度与传递刚度是相等的，因此该方法的测试频率较低，一般小于200 Hz。荷兰代尔夫特理工大学基于频响法搭建了可等效为单自由度系统的锤击试验台，测试了不同种类、不同老化程度的弹性垫层动刚度［12］。韦凯等［13］基于温频等效原理研究了弹性垫层的频变特性。Shen 等［14］建议将基于物理的有限元轨道模型和数据驱动的高斯过程回归模型结合起来，通过现场锤击试验从测得的频率响应函数直接推断轨道部件刚度。Man等［15］通过锤击试验测试了轨道结构的频响函数及动态特性。可见，大量学者从扣件静刚度室内试验方法及标准、动刚度的室内试验方法、测试设备及影响因素等方面进行了研究，但对于服役状态下的扣件动刚度测试方法研究较少。

将钢轨视为置于连续弹性基础上的简支梁，推导扣件动刚度与钢轨1 阶弯曲振动频率的关系，提出基于连续弹性基础梁模型的扣件动刚度测试方法，并采用该方法对某服役状态下的高铁线路轨道扣件动刚度进行测试。

1 基于连续弹性基础梁模型的扣件动刚度计算式

推导扣件动刚度计算式时，基于如下基本假设［16］。

（1）钢轨的应力和应变关系遵循胡克定律。

（2）变形前垂直于轴的平截面在变形后仍保持平面并保持和变形后的轴垂直，即平截面假定。

（3）钢轨满足连续弹性基础梁（文克尔梁）模型的假定，即将基础视为由连续排列且相互独立的线性弹簧组成，每个弹簧的变形仅决定于作用在该弹簧上的力，而与相邻弹簧的变形无关。

（4）忽略阻尼的影响。

根据基本假设，将钢轨视为置于连续弹性基础上的简支梁，长度为L，如图1所示。

图1 连续弹性基础梁模型

钢轨的无阻尼自由振动方程为［17］

其中，

式中：m为钢轨单位长度质量，kg·m－1；E为钢轨弹性模量，N·m−2；I为钢轨截面对水平轴的惯性矩，m4；k为连续分布支承刚度，即钢轨基础弹性模量，N·m－2；K为扣件动刚度，N·m－1；e为弹性支承间距，m；u（x，t）为钢轨微元段的垂向位移，m。

钢轨弯曲自由振动方程式（1）为4 阶偏微分方程，为求其振动解，可采用分离变量法，假定

式中：φ(x)和Y(t)分别为u（x，t）2 个变量的函数。

将式（2）代入式（1）中，则有

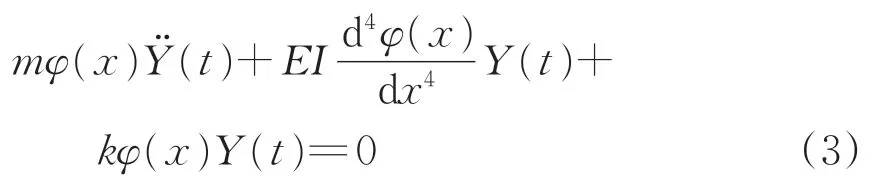
根据文献［18］可知Y(t) =sin(ωt)，ω为系统的固有角频率，则有

式（4）可整理为

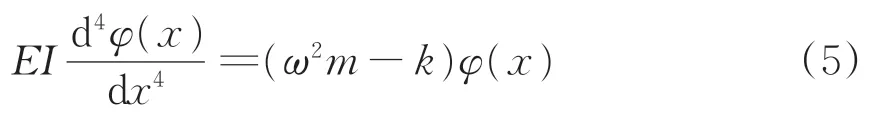
令α4=则有

式（6）的通解为

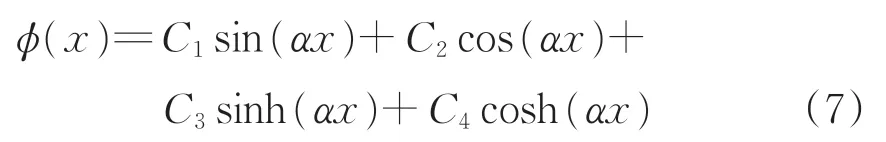
式中：C1，C2，C3，C4为积分常数，由边界条件确定。

简支梁的边界条件为

将式（12）代入式（6）可得

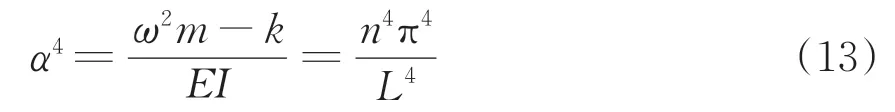
解得ω为

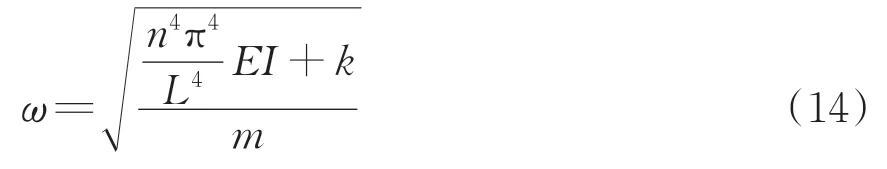
连续分布支承刚度k为

则基于钢轨1 阶弯曲振动频率的扣件动刚度K为

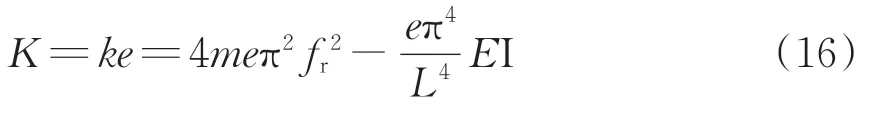
式中：fr为钢轨1阶弯曲振动频率，Hz。

式（16）即为基于连续弹性基础梁模型的扣件动刚度计算式。由式（16）可知，扣件动刚度由钢轨1 阶弯曲振动的频率和参振长度、钢轨的单位长度质量和抗弯刚度以及扣件支承间距决定。可见，对于确定的轨道结构，可通过测量钢轨1 阶弯曲振动频率得到扣件动刚度。

2 仿真验证

扣件动刚度计算式是基于连续弹性基础梁模型推导的，但实际上钢轨应视为弹性点支承连续梁模型，弹性支承间距为扣件间距，如图2所示。本节针对弹性点支承连续梁模型进行仿真计算，验证分析基于连续弹性基础梁模型推导的扣件动刚度计算式的正确性和可靠性。

图2 弹性点支承连续梁模型

采用ANSYS 软件建立钢轨弹性点支承连续梁模型。仿真分析过程中充分考虑钢轨的弯曲和扭转变形，钢轨采用铁木辛柯梁模拟。扣件支承采用线性弹簧模拟。为了消除边界条件的影响，模型长度取100 m。

采用谐响应分析钢轨的弯曲振动频率，即通过计算求得钢轨在某个频率范围内周期循环荷载作用下的周期响应，并得到谐响应值随着频率变化而变化的曲线，从而确定钢轨在以正弦规律变化荷载作用下的响应，得到钢轨的固有频率。仿真分析参数见表1。

表1 仿真分析参数

在扣件跨中和节点分别施加单位正弦荷载，钢轨垂向振动仿真结果如图3所示。由图3可知，当扣件刚度为30 kN·mm−1时，钢轨1阶弯曲振动频率为139 Hz。由式（16）可得，钢轨1阶弯曲振动频率为139 Hz 时，扣件动刚度为29.7 kN·mm−1，与仿真计算中的扣件刚度30 kN·mm−1基本一致，说明基于连续弹性基础梁模型的扣件动刚度计算式是正确可靠的。

图3 钢轨垂向振动仿真结果

频率为139 Hz处的钢轨振型如图4所示。由图4可知：钢轨发生1 阶弯曲振动时，钢轨的参振长度约为62 个扣件间距，即L=62e=40.3 m；在钢轨1阶弯曲振动参振长度中间的一定范围内，钢轨幅值较大，因此采用钢轨1阶弯曲振动频率评估扣件动刚度时，其评估范围l可取为钢轨参振长度L的1/2，约为20 m。

图4 钢轨1阶弯曲振动振型

为进一步分析扣件动刚度计算式的适用范围，分别采用式（16）和弹性点支承连续梁仿真模型进行钢轨1阶弯曲振动频率在50～550 Hz范围内的扣件动刚度计算，结果如图5所示。

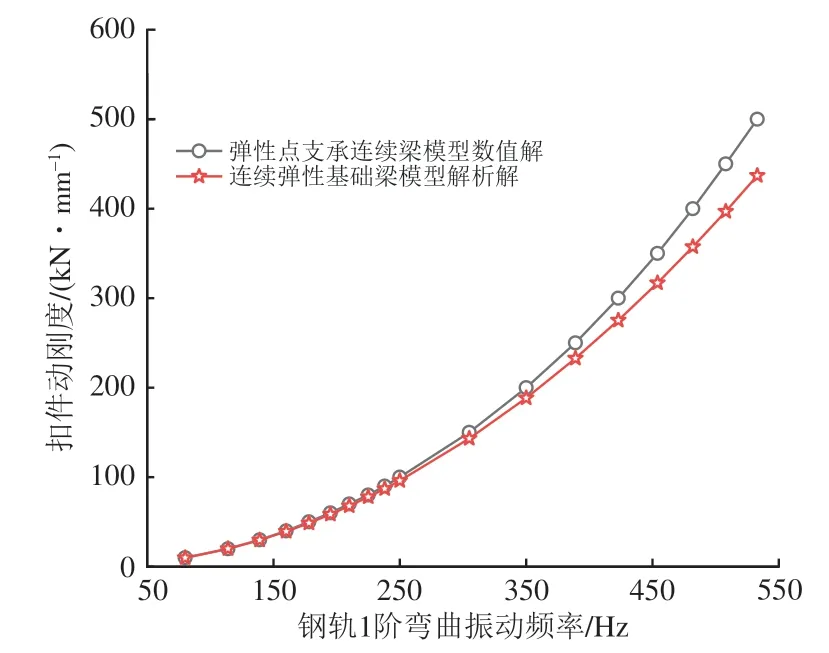
图5 不同钢轨1阶弯曲振动频率下的扣件动刚度

由图5可知：随着钢轨1 阶弯曲振动频率的增大，式（16）和仿真模型所得的扣件动刚度差增大，钢轨1 阶弯曲振动频率在0～300 Hz 时，计算误差小于5%；钢轨1 阶弯曲振动频率在300～450 Hz 时，计算误差为5%～10%；钢轨1 阶弯曲振动频率大于450 Hz 时，计算误差大于10%。可知，基于连续弹性基础梁模型的扣件动刚度计算式在钢轨1 阶弯曲振动频率小于450 Hz 时具有良好的适用性。

3 测试方法

基于扣件动刚度计算式提出服役状态下扣件动刚度的测试方法，该测试步骤如下。

（1）选择钢轨激励方式。由于扣件动刚度与钢轨1 阶弯曲振动频率有关，而与振动幅值无关，因此可利用力锤、激振器或普通锤子对钢轨进行激励。

（2）选择钢轨加速度传感器型号。加速度传感器量程应根据激励方式进行选取，一般量程为500 m·s−2，频率范围大于5 000 Hz。

（3）数据采集系统设置。为了有效测试钢轨的弯曲振动频率，数据采样频率大于5 000 Hz。

（4）在需要测试服役状态下扣件动刚度的区段l范围内布置钢轨加速度传感器，在0.5l处至少布置1 个加速度传感器，当传感器数量大于1 时，应取奇数且相对于0.5l处对称布置，如图6所示。

图6 服役状态下扣件动刚度测试方法示意图

（5）在0.5l处激励钢轨，激励次数至少3 次，并同步采集加速度传感器信号。

（6）对采集的加速度传感器时域信号进行快速傅里叶变换，转换成加速度频域信号，并获得钢轨1阶弯曲振动频率fr。

（7）判定测得的fr是否适用于式（16），若fr≤450 Hz，则可采用式（16）计算扣件动刚度；若fr>450 Hz，则不适用。

（8）若fr≤450 Hz，将fr带入式（16），计算得出服役状态下l区段内的扣件动刚度K。

4 现场应用

采用该方法在某高铁线路上进行了扣件动刚度现场测试。该高铁线路轨道结构为CRTS Ⅱ型板式无砟轨道，扣件采用W300-1 型扣件系统，扣件间距为0.65 m。

首先选择尼龙锤头INV 9313 型号力锤对钢轨进行激励；加速度传感器采用朗斯测试技术有限公司生产的LC0101 型压电加速度传感器，其灵敏度为10 mV·m−1·s2，量程为500 m·s−2，频率范围为0.5～15 000 Hz；数据采样频率设置为10 kHz；在测试扣件动刚度区段20 m 范围内布置1 个加速度传感器，传感器布置在测试区段正中间；用INV 9313 力锤敲击钢轨3 次，获得钢轨的加速度时域信号，如图7所示。

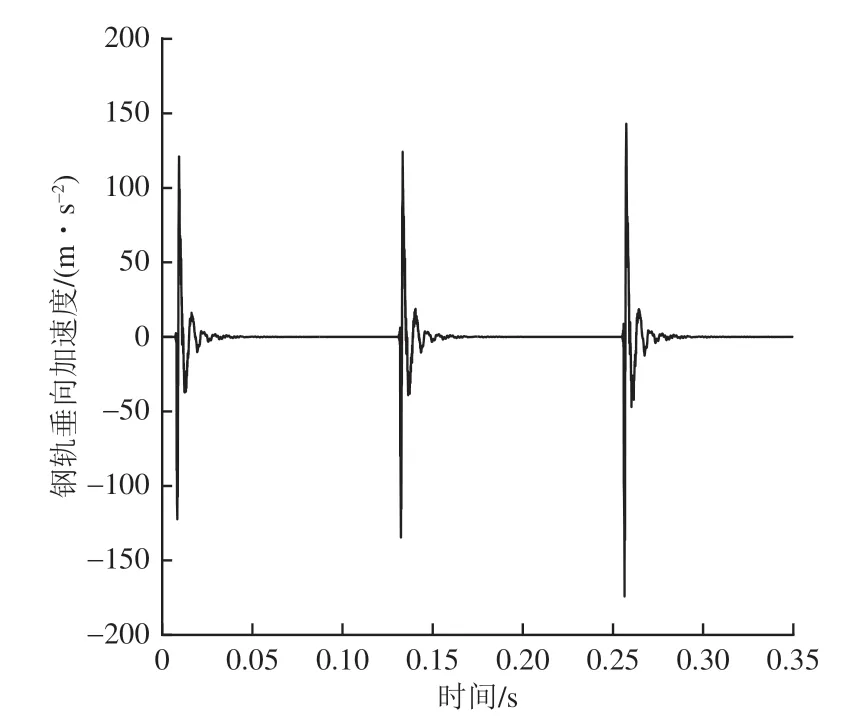
图7 3次敲击钢轨加速度时域图

将3 次敲击后的钢轨加速度时域信号进行快速傅里叶变换，转换成钢轨加速度频域信号，并获得此处的钢轨1 阶弯曲振动频率fr=154 Hz，如图8所示。判定测得的fr≤450 Hz，将钢轨1 阶弯曲振动频率fr代入扣件动刚度式（16），可得该服役状态下的扣件动刚度为36.5 kN·mm−1。W300-1 型扣件垫板的静刚度范围为20～25 kN·mm−1，按设计中值22.5 kN·mm−1考虑，该服役状态下的扣件动刚度为垫板静刚度的1.62倍。

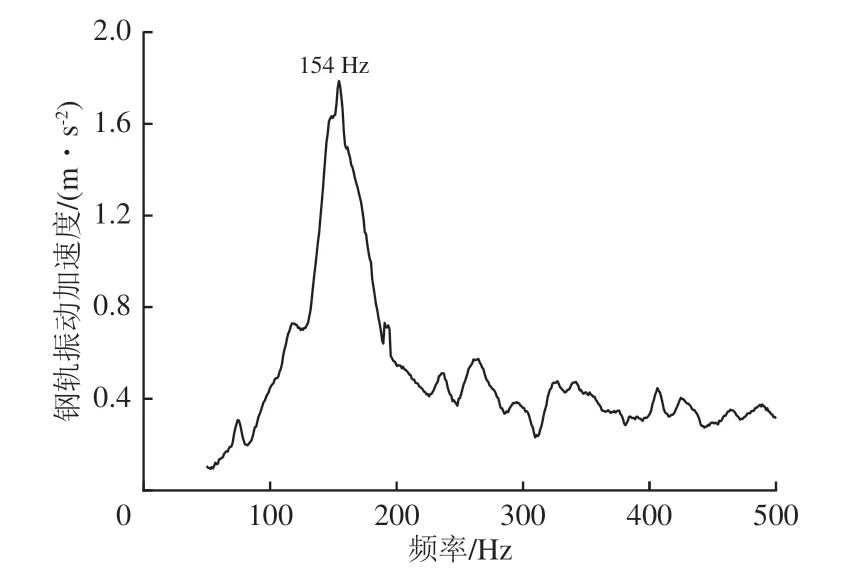
图8 钢轨频谱图

5 结 论

（1）扣件动刚度由钢轨1 阶弯曲振动的频率和参振长度、钢轨的单位长度质量和抗弯刚度以及扣件支承间距决定，当轨道结构确定时扣件动刚度可通过测试钢轨1阶弯曲振动频率求得。

（2）扣件动刚度计算式在钢轨1 阶弯曲振动频率小于450 Hz时计算误差小于10%，准确性较高。

（3）采用基于连续弹性基础梁模型的扣件动刚度测试方法，测试得到某高铁线路CRTS Ⅱ型板式无砟轨道服役状态下的扣件动刚度为36.5 kN·mm−1，约为垫板静刚度的1.62倍。