基于互补滤波的轨道不平顺动态测量方法
陈仕明,魏世斌,李 颖,程朝阳,侯智雄,秦 哲,杜馨瑜
(1.中国铁道科学研究院 研究生部,北京 100081;2.中国铁道科学研究院集团有限公司 基础设施检测研究所,北京 100081)
轨道不平顺是轮轨系统的激扰源,是引起机车车辆振动的主要原因,对行车的安全性、平稳性及舒适性等都有重要影响。轨道高低不平顺会增加车体的垂向振动加速度和轮重减载率,轨向不平顺会增加横向振动加速度和脱轨系数[1]。因此,轨道状态检测对掌握轨道不平顺特征分布、轨道养护维修策略及保障列车行驶安全具有重要意义[2]。
随着列车速度提高,30~200 m 波长的轨道不平顺逐渐开始影响列车运行安全。同时,对于大跨度桥梁与路基沉降的检测需求也逐渐迫切[2]。轨道不平顺检测方式按照有无轮载作用,分为静态检测和动态检测。静态检测结果是工务养护作业的依据,动态检测结果是综合反映轨道结构状态的依据,例如线路中存在的道床暗坑和路基沉降等。按照测量原理,分为绝对测量和相对测量。绝对测量需依赖全站仪等精密测量仪器,以测量准确的高程信息,故检测速度缓慢。相对测量主要分为弦测法和惯性基准法2 类,其中弦测法原理简单,便于现场复核,缺点是测量波形在某些波段存在严重失真;惯性基准法是我国轨道检查车在动态检测中采用的主要方法[1]。传统惯性基准法通过积分和高通滤波等算法处理加速度计和测距传感器数据,实现对轨道不平顺的测量。在测量长波不平顺时,加速度计信噪比低,信号十分微弱,导致传感器积分漂移误差较大。因此,对长波不平顺准确测量仍是亟待解决的问题。
我国对轨道长波不平顺的测量主要采用德国的矢距差法。李阳腾龙等[3]在此基础上提出了高密度四点偏差约束轨道高低模型。杨飞等[4]将矢距差法简化为中点弦测法,提出用60 m 弦测量长波不平顺。王源等[5]采用频率抽样逆滤波设计方法,对弦测测量的传递函数进行补偿。此外,Tsubokawa等[6]为轨检车设计“惯性中弦偏移”法,利用陀螺仪数据推导得到弦测值。另外,将组合导航的方法引入到轨道检测中的研究方法越来越受到重视[7−9]。Chen 等[7]为相对测量轨检小车集成卫星定位与惯性组合导航(GNSS/INS)技术,该方法脱离了全站仪等高精度设备,因此测量速度相对较快。Li等[8]在轨检小车上配备激光辅助惯性导航系统,对钢轨的三维曲线进行测量,但需要人为设置控制点。Jiang 等[9]克服了高精度控制点的要求,提出结合零速度更新技术的基于惯性导航的轨道不平顺测量方法。这些方法通过引入其他传感器作融合计算,可以测量得到轨道长波不平顺。但往往系统复杂,要求检测速度较低,且GNSS定位信号容易在过隧道时丢失,并不适用于高速列车的动态检测。
利用车载传感器进行高速动态检测可有效提升检测效率,是当前轨道检查车上主要采取的方法。文献[10−12]讨论了采用安装在构架上的陀螺仪测量不平顺的方法,发现在低速条件下陀螺仪的测量结果更加准确。Westeon 等[11]指出该陀螺仪测量方法测量短波不平顺时会产生衰减。熊丽娟等[13]分析了地球自转对陀螺仪测量的影响。在此基础上,Escalona 等[14]分析了采用加速度计和陀螺仪测量系统的传递函数,并引入组合测量方法,但采用的巴特沃斯滤波会带来非线性相位变化。由于安装条件限制,以上方法往往用车体或转向架角度近似轨面角度变化,带来的误差降低了轨道长波不平顺的测量精度。因此,Tsubokawa 等[6]在转向架前后安装测距传感器以补偿陀螺仪信号,并且为避免惯性传感器积分漂移,提出用1 阶差分描述轨道平顺性变化。
本文提出一种应用于高速轨道检查车平台的轨道不平顺动态测量方法。首先基于新型机械安装结构,在轨面上构建“两点弦”测量模型并推导出角速度测量算法;之后根据系统传递函数幅频特性,设计互补滤波方法,以补偿角速度测量法在短波不平顺处的衰减;最后以检测速度选定合适的测量算法。
1 传统测量系统和方法
1.1 测量系统
轨道不平顺测量系统主要由惯性测量单元(Inertial Measurement Unit,IMU)、激光器和CCD 相机集成的激光摄像组件及编码器等传感器组成[15]。当前广泛应用的GJ-6 型轨道检测系统将IMU 与激光摄像组件安装在检测梁上,根据编码器脉冲信号对传感器进行空间采样,采样周期为0.25 m[16]。其中激光摄像组件采用线结构光的三维视觉检测模型,可解算出轨面特征点相对于相机的位移,分辨率高达0.1 mm。IMU 包含3 轴加速度计与陀螺仪,惯性传感器由于受到积分漂移和列车振动的影响,测量误差随时间累积。
1.2 惯性基准法
动态测量基准坐标系以轨面中心点为坐标原点,x轴正向指向列车前进方向,y轴正向沿水平方向向左,z轴正向垂直于大地向下。
在实际工况条件下,由于转向架与轴箱之间存在一系悬挂,检测梁上的加速度计只能反映转向架的位移变化。因此,利用激光摄像组件提供的测距信息测量轨面与转向架之间的相对位移,并与加速度计信号结合,计算得到轨道不平顺值。该算法表示为

式中:和分别为轨向和高低不平顺的测量值;am为加速度计测量值;g为重力加速度;θb为转向架侧滚角;t为时间;G为标准轨距值,即1 435 mm;δyi和δzi分别为测距传感器输出的横向和垂向位移;l和r分别为左右2侧。
式(1)给出的基于加速度信号和测距传感器数据的高低和轨向不平顺的惯性基准法常应用于传统的轨道检测系统,本文称之为加速度测量法。在实际应用中,加速度计测量高低不平顺时,理论上敏感轴需要始终与水平基准线相垂直,但转向架运行过程中会产生6 个自由度的车体振动,加速度计敏感轴方向发生随机变化。这种方法在测量短波轨道不平顺时具有较高精度;在测量长波轨道不平顺时,加速度计敏感值小、信噪比低,积分漂移误差较大,测量精度有所下降;在低速检测环境下,时间域采样率降低,测量结果会迅速漂移。
2 测量系统和方法优化
2.1 系统优化
在GJ-6 型检测系统的基础上优化了机械安装结构,如图1所示。新系统统一设计了转向架与检测梁,并在转向架前后的2 个端部安装检测梁,并在检测梁中安装激光摄像组件与IMU。理论上,该系统可以利用光纤陀螺仪具有的低漂移和高精度的特点,提升系统测量精度。

图1 机械安装结构
2.2 角速度测量法
基于改进的硬件结构,考虑光纤陀螺仪测量误差项,推导角速度测量法。由于检测梁与转向架固定连接,因此对应的测量模型只考虑转向架与轴箱之间的一系悬挂,测量模型如图2所示。图中:ψ为轨面切线俯仰角,即轨道的垂向切线与轨面纵向基准线x轴之间的夹角;ϕ为轨面切线摇头角,即轨道的水平切线与轨面纵向基准线x轴之间的夹角;ψb和ϕb分别为转向架的俯仰角和摇头角;x处的高低轨道不平顺为Z(x),轨向不平顺为Y(z);x和x-L位置处轨顶点连线构成的“两点弦”,在基准坐标系下的俯仰角记为ψ′,摇头角记为ϕ′;v为行车速度。

图2 轨道不平顺测量模型
根据文献[11]可知,基于角速度测量轨道不平顺(包括高低和轨向不平顺)的简化表达式为

式中:ds为空间域微分算子;ωy为ψ的1 阶微分;ωz为ϕ的1阶微分。
由式(2)可知:对于高低不平顺的测量,可以通过对角度ψ的空间域积分得到;对于轨向不平顺的测量,可以通过对角度ϕ的空间域积分得到。
以高低不平顺测量为例,由于转向架与车轮之间存在一系悬挂,轨面切线俯仰角ψ难以通过安装在检测梁上的传感器直接测量获得,一般采用转向架姿态角ψb对ψ进行近似[11−12]。测量30 m 以内的短波不平顺时,近似引起的误差较小;测量中长波不平顺时,陀螺仪理论信号微弱,近似误差导致信噪比较低,尤其是当列车与轨道之间存在共振时。
在测量高低不平顺时,用ψ′代替ψ代入到式(2)进行测量计算;同理,测量轨向不平顺时,用ϕ′代替ϕ,代入到式(2)。由图2可知,角度ψ′和ϕ′可使用当前安装的传感器进行观测。设定ψ′和ϕ′的1 阶微分表示为ω′y和ω′z,设定γz=ψb−ψ′,γy=ϕb−ϕ′,2 者的1 阶微分分别表示为和。因此,角速度测量算法可以表示为

式中:ωb为转向架三轴角速度。
激光摄像组件测量转向架与轨道之间的相对位移测量模型如图3所示。图中:L为前后检测梁的纵向距离;δB,y,r为后右侧相机相对于轨面的横向位移,δF,z,l为前左侧相机相对于轨面的垂向位移,其余变量类似。由图2和图3可知,变量和可以表示为

图3 测距组件测量模型示意图

式中:Δt为2次空间采样时间间隔;k为离散时间。
轨道检测中一般采用欧拉角描述转向架姿态,三轴分别表示为θb,ψb和ϕb。转向架3 轴角速度ωb与陀螺仪测量角速度ωm的等式关系参考文献[17],考虑到列车行驶过程中转向架姿态变化规律,忽略掉式中的2 阶项,并将余弦项近似为1,可以简化为

另外,考虑到地球自转对光纤陀螺仪测量的影响,对误差项进行补偿。陀螺仪测量角速度在载体坐标系下的地球自转分量主要由纬度决定,表示为[13,18]

式中:W为纬度;ωIE为地球自转角速度。
考虑上述误差项,将式(5)和式(6)代入到式(4),可得

根据式(7)可对高低、轨向不平顺进行测量,称之为角速度测量法。一般来说,由长波不平顺激励的传感器信号十分微弱,高精度的光纤陀螺仪可以提升测量精度。同时该算法通过构建基于“两点弦”的测量模型,直接建立传感器测量值与轨道不平顺之间的联系,因此在理论上不受传感器敏感轴方向变化的影响,可提高系统的重复性精度。
2.3 测量效果
“两点弦”测量模型与弦测法类似,都是采用在轨面上拉弦的方法,因此测量值相比真实值会发生形变。由于轨道不平顺为随机不平顺,包含不同的波长成分,为研究算法在测量不同波长轨道不平顺的幅值和相位变化,需要分析系统的传递函数。
由于高低与轨向不平顺在角速度测量原理上的一致性,对二者统一分析。由图2可知,角度ψ′与轨道不平顺之间的关系为
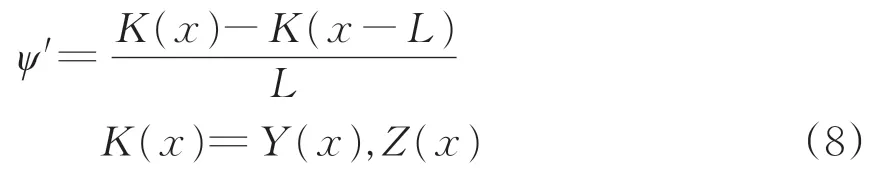
式中:K(x)为真实轨道不平顺。
对式(8)进行傅里叶变换,得到角度ψ′与轨道不平顺的传递函数H′(Ω)为

其中,

式中:Ψ为空间域频率;Ω为时间域频率;λ为波长。
将式(9)代入到式(4),得到角速度测量法的传递函数Hω(s)为

其中,
s=j2πΨv
式中:s为时域拉氏算符。
测量系统的幅频特性曲线反映了测量结果与真实不平顺之间的关系,根据式(12)得到角速度测量法的幅频特性曲线如图4所示。由图4可以看出,该方法在测量0~20 m 区段的短波轨道不平顺时存在明显衰减,测量10~100 m 区段时存在非线性相位畸变,对整体测量精度影响较大,仍存在优化与改进的空间。

图4 测量系统的幅频特性
实际测量系统为离散系统,因此对传递函数作离散化处理。常用的离散方法有反向差分法、双线性变换及脉冲响应不变法等[19]。其中反向差分变换法由于形式简单在实际工程中应用广泛,形式为

式中:T为采样时间间隔。
将式(11)代入式(10),得到z域离散传递函数Hω(z)为
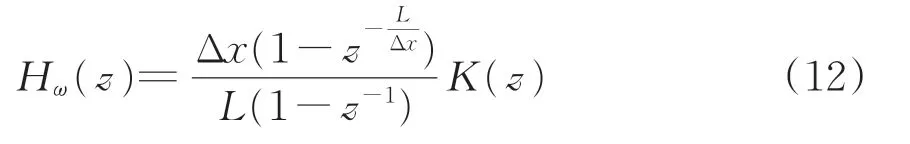
式中:系统固定空间采样间隔Δx为0.25 m,前后测距组件纵向距离L为4.8 m。
设定M=LΔx−1,近似为整数20。那么离散测量系统可以近似为

其中,

由式(13)可知,角速度测量法的测量结果相当于真实不平顺经过形为矩形窗的低通滤波器。
传统的加速度测量法通过对加速度计数据积分计算轨道不平顺,因此在理论上计算结果直接反映轨道不平顺。加速度测量法的传递函数Ha(z)表示为

2.4 互补滤波测量算法
为解决角速度测量法在测量短波轨道不平顺时存在衰减的问题,引入互补滤波测量法。
从式(1)和式(4)可知,轨道不平顺测量方法均需经过2 次积分计算。由系统随机噪声积分产生的低频漂移及线路中的曲线和坡度等叠加形成无价值的趋势项,常用高通滤波器法、拟合多项式法及小波变换法等将其消除[10]。轨道检测系统采用窗函数法设计高通滤波器。
设计满足截止频率(或截止波长)要求的无限脉冲响应(FIR)低通滤波器,传递函数为F(z),对应高通滤波器传递函数为1−F(z)[19]。级联滤波器传递函数为F(z)和w(z),对应高通滤波器传递函数为Γ(z)=1−w(z)F(z)。若系统采用传递函数为Γ(z)的滤波器去除低频漂移,则测量结果与真实不平顺的传递关系为

式中:H(z)为测量系统传递函数。
将式(13) 和式(14) 代入式(15),可简化为

其中,
Fa(z)=1−w(z)
Fω(z)=1−F(z)
由式(16)可知,加速度测量法和角速度测量法的测量结果分别经过传递函数为Fa(z)和Fω(z)的2 个滤波器并累加,可计算出轨道不平顺。本文将该方法称为互补滤波测量法,2 个滤波器的组合形式为Γ(z)。
假设传递函数Γ(z)的截止波长为120 m,则传递函数Fa(z),Fω(z)及Γ(z)的幅频特性曲线如图5所示。从图5可以看出:传递函数Fω(z)与Γ(z)的幅度谱曲线相近,截止波长为63 m;传递函数Fa(z)的截止波长为6.6 m。

图5 滤波器幅度谱对比
进一步,根据式(16)得到3 种方法的测量范围如图6所示。从图6中可以看出:互补滤波测量法利用角速度测量法测量10~120 m 的中长波不平顺,利用加速度测量法测量1.5~10 m 的短波不平顺。

图6 各算法测量范围
在实际应用中,加速度测量法在测量短波不平顺时精度较高。互补滤波测量法是利用加速度测量法的结果,对角速度测量法进行有效的补偿。
高通滤波器Γ(z)(或长波滤波器)性能直接影响测量精度。采用多个矩形窗与三角窗级联再并联,设计得到本文所用的长波滤波器。对比新设计长波滤波器与GJ-5,GJ-6 型系统所用滤波器的幅频特性如图7所示。滤波器的性能指标一般有通带抖动幅度和过渡带宽,由图7可以看出,该方法改善了GJ-6 型所采用长波滤波器的通带抖动大小,过渡带宽和阻带截频等基本保持不变。

图7 长波滤波器幅频特性
在实际应用中,当轨道检测系统速度低于40 km·h−1,加速度测量法结果变化剧烈、幅值较大,会降低互补滤波测量法的测量精度。因此,根据检测速度选择互补滤波测量法或角速度测量法,实现最高截止波长为200 m 的4 种不同波长的轨道不平顺测量,算法流程如图8所示。

图8 算法流程框图
3 试验与数据分析
为评估算法精度,同时避免传感器采集和同步误差带来的影响,建立多体动力学模型,收集转向架的振动响应和运动数据,将3 种算法计算结果与参考不平顺对比,综合分析检测速度和传感器噪声系数对测量结果的影响。
3.1 多体动力学分析
整车建模时将车体、构架和轮对考虑为多刚体,车辆由1个车体、2 个构架、4个轮对及8个轴箱组成,共计62 个自由度。其中一系、二系减振器统一采用非线性弹簧阻尼元件代替,车体参数参考动检车中较为普遍使用的CRH2C型列车,利用UM软件搭建多体动力学整车模型如图9所示[20]。

图9 车辆-轨道耦合动力学模型(CRH2C)
取列车行驶速度为180 km·h−1,空间采样间隔为0.25 m,模拟计算结果如图10所示。从图10可以看出:转向架垂向位移与高低不平顺较为接近,而横向位移幅值比轨向不平顺大;转向架的摇头角相比俯仰角幅值更小,低频变化更为明显。

图10 车辆-轨道耦合动力学仿真结果
3.2 传感器噪声建模
在测量过程中,IMU 的零偏在初始校准期间归零,但会随着时间增长产生漂移。这主要是因为温度变化、电源电压变化或材料老化等。目前评价光纤陀螺仪性能的主要指标为零偏稳定性,系统所采用的陀螺仪精度指标为1°·h−1(100 s平滑)。
Allan 方差分析法是常用的误差分析法,可以综合分析陀螺仪的性能,得到各项静态误差指标[22]。静置光纤陀螺仪2~3 h 并采集数据,采用Allan 方差进行标定,得到零偏不稳定性为0.092°·h−1,速率随机游走为0.39°·h−1.5,角度随机游走为0.008 4°·h−0.5。其中零偏不稳定性和角速率随机游走是引起陀螺仪长期漂移误差和影响惯性测量系统性能的主要因素[21],因此陀螺仪随机误差可建模成角度随机游走和角速率随机游走之和。设定陀螺仪随机误差为sm,表示为

式中:wN和wK均为零均值的白噪声,分别对应角度随机游走和角速率随机游走误差;b(t)为噪声wK的积分。
噪声的自相关函数表示为

式中:E 为期望;σ2N为角度随机游走白噪声方差;σ2K为角速率随机游走白噪声方差。
对随机误差进行离散采样,得到wN(k)和wK(k),二者的方差分别表示为σ2NΔt−1和σ2KΔt,Δt为采样时间间隔。对于加速度计,通常采用零均值白噪声模型,方差记为σ2。
3.3 试验结果对比
以某段高铁线路综合检测车实测不平顺数据作为动力学模型输入,对收集的加速度和角速度等动力学响应加入随机噪声,分别用加速度测量法、角速度测量法及互补滤波测量法计算得到测量值。采用Welch法对试验结果进行谱分析,段内傅里叶变换点数为4 096,加矩形窗,段与段间数据样本重叠50%,试验结果与功率谱密度幅值(PSD)曲线如图11所示,图中参考不平顺为动力学模型的输入不平顺。

图11 测量结果对比
从图11可以看出:3种方法的结果与参考不平顺波形相近,其中加速度测量法测量结果幅值略大于其他算法;角速度测量法测量结果在高频部分(1~20 m)与参考不平顺相比有明显的衰减,在L处达到极小值,与理论分析一致;而加速度测量法在低频部分(100 m 以上)有较大增益;相比之下,互补滤波测量法的PSD 曲线的低频部分与角速度测量法一致,高频部分经过互补滤波算法有效补偿后,整体上最为接近参考不平顺。
设定不同的检测速度和噪声系数,试验条件见表1。表中噪声系数为标定值,其中陀螺仪的速率随机游走系数均为0.39°·h−1.5。选取长波滤波器的截止波长分别为120 和200 m,统计3 种算法测量结果的误差绝对值均值(MAE)和均方根误差(RMSE)见表2。由表2可以得出以下结论。

表1 试验条件

表2 试验结果 mm
(1)测试1 中,在高速下的角速度测量法与加速度测量法测量误差接近,均有较高精度。当截止波长为200 m 时,互补滤波测量法精度更高,相对于加速度测量法,互补滤波测量法在测量高低和轨向不平顺时平均精度分别提升24% 和58%,RMSE 分别降低0.10 和0.19 mm。在当前条件下互补滤波测量法的精度提升空间较小。
(2)测试2 相比测试1 增加了传感器噪声系数。当截止波长为200 m 时,加速度测量法的MAE 增加了1 倍,受噪声系数影响明显;角速度测量法和互补滤波测量法的测量精度基本不变。相比于加速度测量法,互补滤波测量法在测量高低和轨向不平顺时平均精度分别提升59.5%和54.9%,RMSE 分别降低0.64 和0.45 mm。系统长时间服役后,传感器精度会逐渐降低,此时互补滤波算法有较为明显的优势。
(3)测试3 相比测试1 降低了检测速度。加速度测量法在低速下表现较差,MAE 增加了0.60~0.70 mm;而角速度测量法和互补滤波法的测量精度基本维持不变。相比于加速度测量法,互补滤波测量法测量高低和轨向不平顺时平均精度分别提升73%和80%,RMSE 分别降低0.9 和1.0 mm。此外,对于互补滤波测量法,轨向比高低不平顺的测量精度更高。从图10可看出,这是因为转向架在水平方向上比垂直方向变化较慢、且幅值较大。因此振动噪声更小,传感器信噪比更高。
选取综合检测车在某高铁高速线路下实际采集的传感器数据作为分析对象,对比加速度与角速度2 种测量方式在低速至停车条件下的高低不平顺测量结果如图12所示。

图12 低速下轨道高低不平顺测量
从图12可以看出:当检测速度在40 km·h−1以上时,角速度测量法与加速度测量法结果趋势基本吻合;当列车以低速行驶直至停车时,加速度测量法测量的高低不平顺产生了异常大值,而角速度测量结果始终在零基线附近,此时角速度测量法更能反映真实的轨道状态。因此对于目前的检测系统,根据速度选择测量算法是有必要的。
综上,互补滤波测量法可有效提升传统加速度测量法的精度,尤其是在系统噪声系数较大或低速检测的条件下。在实际情况中,当列车在某条固定线路重复检测或正反向检测时,转向架振动引起的加速度计敏感轴方向变化直接影响测量精度。互补滤波测量法则有效抑制了这一部分误差。
此外,从算法执行效率来看,互补滤波测量法仅融合传统测量法与角速度测量法,复杂度较低且各算法模块之间耦合性较弱,满足现有高速动检车轨道检测系统以350 km·h−1速度检测的实时处理要求。
4 结 论
(1)通过在转向架前后安装测距传感器,从而在轨道上构建了“两点弦”,建立传感器数据与轨道变化之间的对应关系,推导出角速度测量法,能够避免传感器敏感轴方向不规律变化对测量结果的影响。
(2)系统传递函数的幅频特性表明,角速度测量法在测量短波轨道不平顺时存在明显衰减。互补滤波法可以有效利用传统方法在测量短波不平顺时的优势,对角速度测量法进行补偿。
(3)在测量长波轨道不平顺时,检测速度和传感器噪声系数对加速度测量法测量精度影响较大。由于光纤陀螺仪的低漂移特性,2 者对角速度测量法影响较小。在实测数据中,加速度测量法在低速检测下精度较差,角速度测量法有明显改善。
(4)数值仿真结果表明,相比于传统算法,互补滤波测量法的测量精度可提升24%~80%。

